拉伸载荷下双销式履带板强度计算方法

曾子豪, 张京东, 龚雪莲, 刘坤明, 桂学文, 廖日东

(1. 北京理工大学 机械与车辆学院，北京 100081; 2. 北方车辆集团有限公司，北京 100072)

0 引言

履带是重型履带车辆的关重件，它将地面的牵引力、附着力和制动力传给车体，并为负重轮提供一条连续滚动的轨道，可大大提高车辆在松软地面的通过性[1]。履带的功能要求决定了履带的工作环境恶劣、载荷复杂，因此履带是履带车辆可靠性的薄弱环节。

履带的具体失效形式多种多样，包含履带板开裂以及断裂、履带销胶套磨损、端连器断裂、端连器磨损、履带板胶块点蚀、脱落等[1-3](见图1)。履带板的开裂、断裂是履带系统中一种常见的故障，而履带的断裂失效将导致车辆无法行驶。长期以来，履带在履带车辆上的消耗与备件量都很大，一旦在战时发生履带失效，更是可能导致严重后果。因此，如何在满足轻量化的要求下提高履带可靠性，一直是装甲车辆工程领域努力的重要方向。而要提高履带的可靠性，最有效的措施莫过于探明履带板在不同工况下的应力应变分布情况，以便有针对性地开展结构设计。

图1 履带常见失效形式Fig. 1 Common failure modes of track shoes

拉伸载荷作为履带板所受的主要载荷，在设计以及强度校核中占有重要地位。装甲车辆设计计算的经典书籍均用最大牵引力P进行履带板与履带销轴尺寸设计[2-4]。黄雪涛等[5-6]利用理论估算得到了拉伸载荷在履带环上的分布，并通过仿真对比验证了其准确性。Liu 等[7]和刘维维[8]运用名义应力法计算了橡胶履带上的拉伸应力，估算了履带的疲劳寿命。Huh 等[9-10]建立了履带行驶系统的多体动力学模型，计算履带拉力在不同工况下的分布。Wang 等[11-12]理论计算了履带上的拉力分布，并利用模型提出了履带拉力的控制策略。

针对拉伸载荷作用下履带的强度分析与计算开展了许多。雷雪媛[13]、雷有功[14]以设计牵引载荷作为基础，利用有限元方法得到履带板在最大牵引力作用下的应力分布，韦泽乾[15]、杨航宇[16]建立二维的履带车多刚体模型，对爬坡，过壕沟等工况进行仿真，得到履带不同工况下的最大牵引力数值，校核了履带板多种工况中牵引力作用下的履带板强度。

上述文献对履带的强度进行了分析与计算，但是均将履带视为一个二维环带，忽略了履带在宽度方向上的载荷分布不均的情况，而载荷分配对履带板强度会产生影响。

履带的连接部件载荷分配不均的情况主要体现在两个方面：1)连接部件如端联器与诱导齿上承受的载荷大小差异；2)连接部件上作用于销轴上的载荷不是按照均布载荷进行分配。对于第2 项，现在已经可以用有限元方法建立连接部件与销轴的接触来进行计算，因此双销式履带拉伸载荷下强度计算的关键在于如何准确给定连接部件上拉伸载荷大小的分配，以及探明载荷分配不同时履带板上应力结果的差异。

文献[17]利用土木力学中的弹性地基梁法对坦克销轴受力进行分析，得到了单销式履带板上载荷分配结果，但是弹性地基梁法忽略了剪切应力的作用，对于金属连接部件的载荷分配计算可能会造成较大误差[18]，并且计算所需的连接部件支撑刚度均是通过试验得来。该方法需要试验数据配合，且其精度需要进一步的研究，因此也无法满足对履带板受拉伸载荷下强度校核的需求。

针对上述情况，本文通过单、双板拉伸试验与对应仿真，验证双销式履带连接部件上的载荷分配与应力分布会随履带板数目的增加而变化的假设，并基于有限元方法进行迭代计算得到履带连接部件上的载荷分配与应力结果，提出一种两步法快速得到履带连接部件上的载荷分配，最后探究履带拉伸强度试验中履带块数对履带应力结果的影响。

1 单板、双板履带板拉伸试验与仿真

某型装甲车辆双销式履带板结构如图2(a)所示，履带板与销轴之间压入橡胶衬套，履带板与履带板之间由端联器与诱导齿连接。

履带车辆在正常行驶过程中，履带环拉伸载荷传递关系如图2(b)所示。主动轮与履带端联器相互啮合，将拉伸载荷F1、F2传递至连接结构(端联器与诱导齿)上，接着逐级传递至每块履带板上。而随着拉伸载荷按照连接结构→履带板的逐级传递，履带环上拉伸载荷的传递发生变化(见图2中，为了研究拉伸载荷在履带上分配(诱导齿上拉伸载荷F1、F1'与端联器上拉伸载荷的差异以及不同拉伸载荷对履带板强度的影响。基本思路是比较在给定拉力下不同数量履带板上的应力以及载荷的差异，基于上述思路同时结合现有条件，本文开展单块板与双块板拉伸仿真与试验。

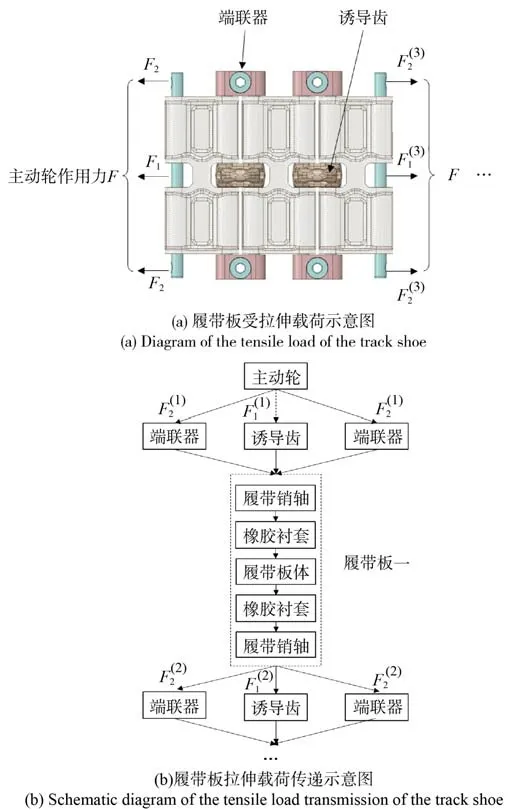
图2 履带板受拉伸载荷示意图Fig. 2 Schematic diagram of track shoe under tensile load

1.1 单板与双板履带拉伸试验

履带板拉伸试验如图3 所示，单、双块履带板分别由工装与拉伸试验机相连。履带板表面贴有应变片作为工作片记录不同拉力下对应的应变值，为了平衡温度的影响，在未进行拉伸试验的履带板贴上应变片作为温度补偿片，将工作片和补偿片分别与动态应变仪桥盒连接，桥盒与动态应变仪和数据记录仪器连接。

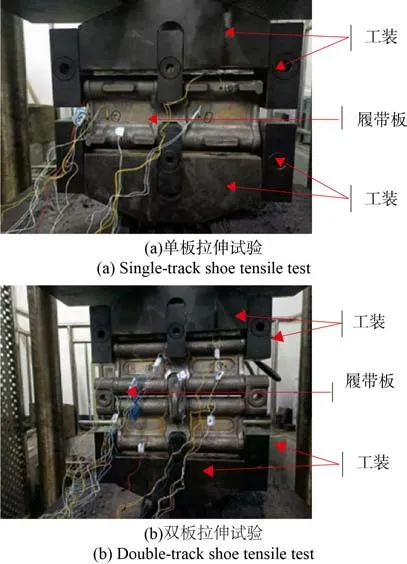
图3 单板双板履带拉伸试验图Fig. 3 Tensile test diagram of single and double track shoes

拉伸试验机以2 kN/s 的速度均匀加载，记录履带板上测点在拉伸载荷作用下对应的应变值。图4为单块与双块履带板上相同一点处的拉力-应变曲线，与单块履带板拉伸相比，在相同拉力作用下，双板拉伸应变值数值明显更大(见表1)，这表明在相同拉伸载荷作用下，双块履带拉伸的载荷分配与单块履带拉伸载荷分配相比发生变化，这样才会使得履带相同位置处的应力相应的发生变化。

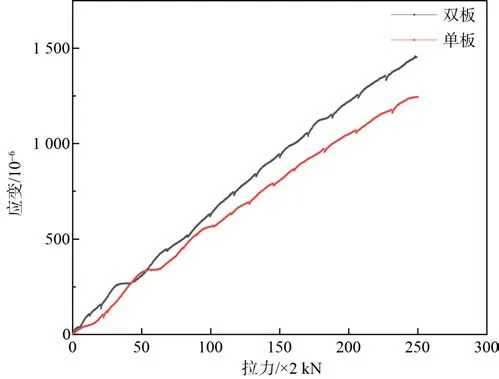
图4 单双板履带相同位置处履带拉力-应变曲线Fig. 4 Track tension-strain curve at the same position of single and double tracks

表1 单双板履带相同位置处履带应变对比Table 1 Comparison of track strain of single and double tracks at the same position

要进一步探明载荷分布差异的大小，需要对履带板的载荷大小分配进行测量。由于条件限制，试验中测量载荷分配大小较为困难，因此开展两次试验的有限元仿真，对单块，双块履带板在相同拉力下载荷分配进行比较。

1.2 单板与双板履带拉伸有限元计算

履带板拉伸仿真计算如图5(a)、图5(b)所示，在工装上施加均匀均匀增大拉伸载荷加载。由于加载情况较为简单，履带板结构具有对称性，分别对单板以及双板，建立对称模型如图5(c)所示。

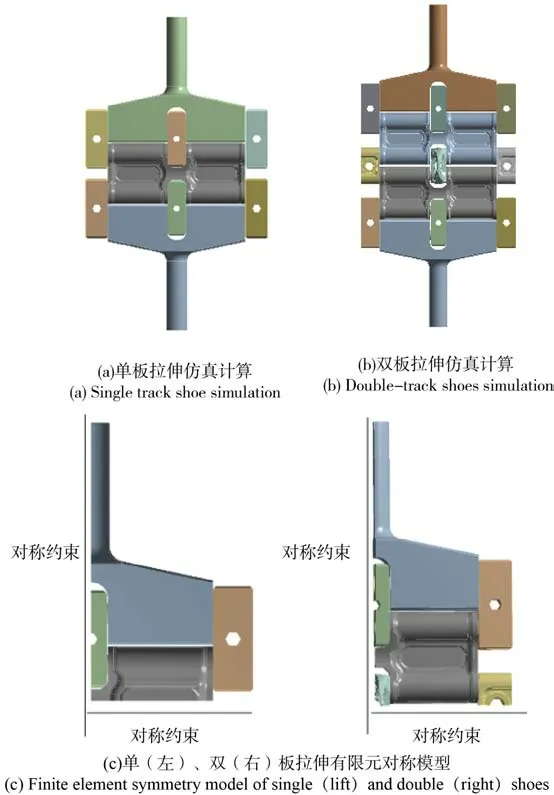
图5 单板双板拉伸有限元计算模型Fig. 5 Finite element calculation model of single and double shoes

仿真计算中，履带与连接部件(端联器、诱导齿)以及工装通过表面接触进行拉伸载荷的传递。部件与部件间采用的是有限滑动接触模型，接触刚度影响着最终结果的精度与仿真收敛性。因此比较不同接触刚度系数(0.1, 1, 10, 100)下最大应力结果来验证仿真的准确性。如表2 所示，当接触刚度系数大于1 时，仿真结果趋向稳定，仿真中取接触刚度为1。切向接触采用Coulomb 摩擦模型，摩擦系数设置为0.2。

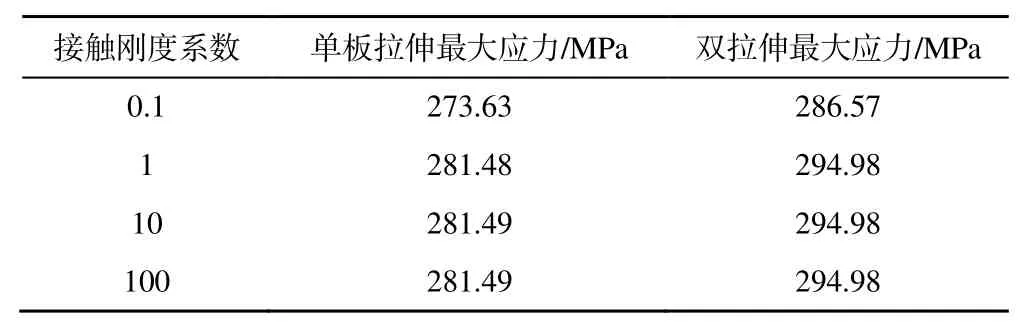
表2 接触刚度与最大应力关系Table 2 Relationship between contact stiffness and maximum stress

橡胶金属铰链内，橡胶衬套被粘结在履带销轴上，并且被一起压入履带销耳内。其压紧度要求橡胶衬套在销耳内不能转动，仿真中橡胶衬套与销耳、销轴均采用绑定接触，不会产生相对滑动。同时橡胶应填满销耳的全部空间[2]，在仿真中将橡胶衬套建模为圆筒形状以充满销轴与销耳的间隙。

橡胶衬套初始压入应力约为1~3 MPa[2]，远小于履带受拉伸载荷时的应力大小，因此忽略橡胶衬套初始压入应力的影响。

对仿真模型进行网格无关性分析，履带板上销耳处是履带板的薄弱部件[17]，因此选取销耳处最大应变作为网格无关性分析指标，如图6(a)所示，整体网格进行逐步加密，得到网格与销耳处最大应变的关系如图6(b)所示，当网格整体尺寸达到2 mm时，最大应变趋于定值，因此选取整体网格尺寸为 2 mm。履带板及连接部件网格模型如图7所示。

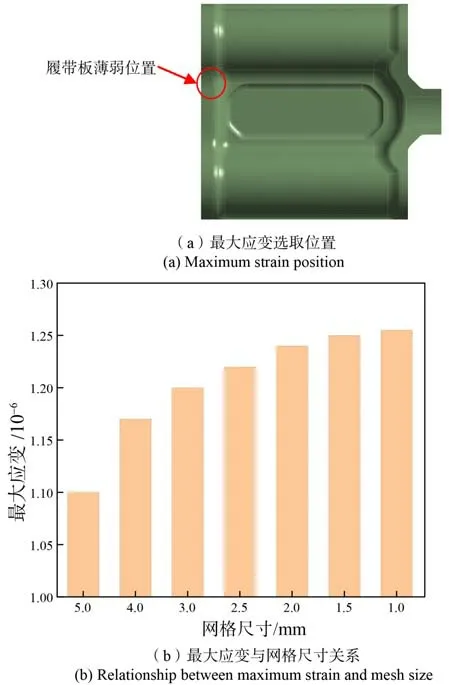
图6 网格尺寸与最大应变关系Fig. 6 Relationship between mesh size and maximum strain

图7 有限元仿真部件网格模型Fig. 7 Finite Element Simulation Part Mesh Model

设计过程中，该型装甲车辆双销式履带所受的最大牵引力p=0.65mgφ=152 kN，m为履带车辆的总质量，g为重力加速度，φ为履带对地面的附着系数，仿真中比较最大牵引力作用下履带板应力分布结果。

履带板、端联器、诱导齿及工装均由合金钢制成，中间的橡胶衬套采用弹性模型，由文献[18]中资料，可以等效取弹性模量为8.5 MPa，履带材料参数性能如表3 所示。

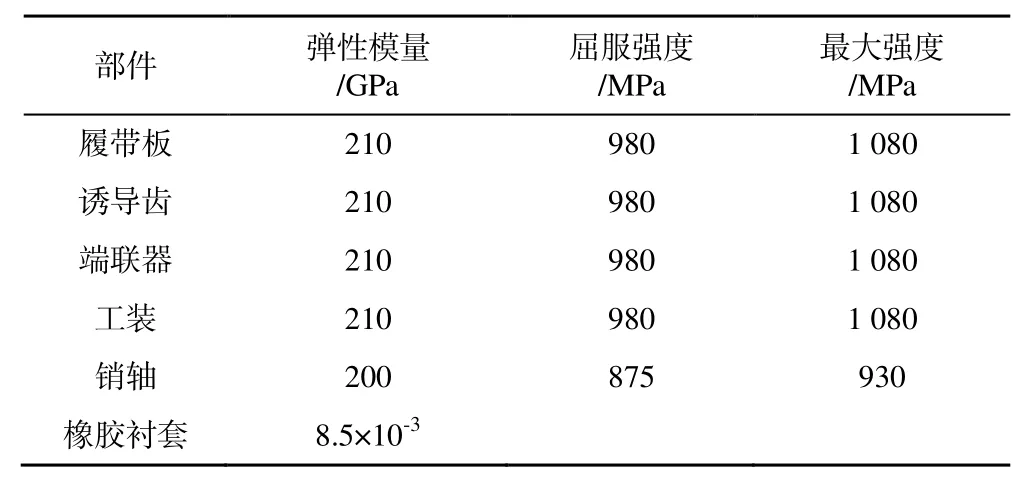
表3 履带板部件材料参数Table 3 Material parameters of track parts

1.3 单板与双板仿真结果验证与分析

1.3.1 单双板拉伸仿真结果验证

选取最大拉伸载荷p作用下，履带板拉伸试验结果与仿真结果进行比对，以此验证仿真的准确性。试验与仿真的结果比对如图8、表4 所示，单板仿真与试验最大误差为6%，双板拉伸仿真与试验最大误差为11%，整体误差较小，可以验证仿真结果的准确性。

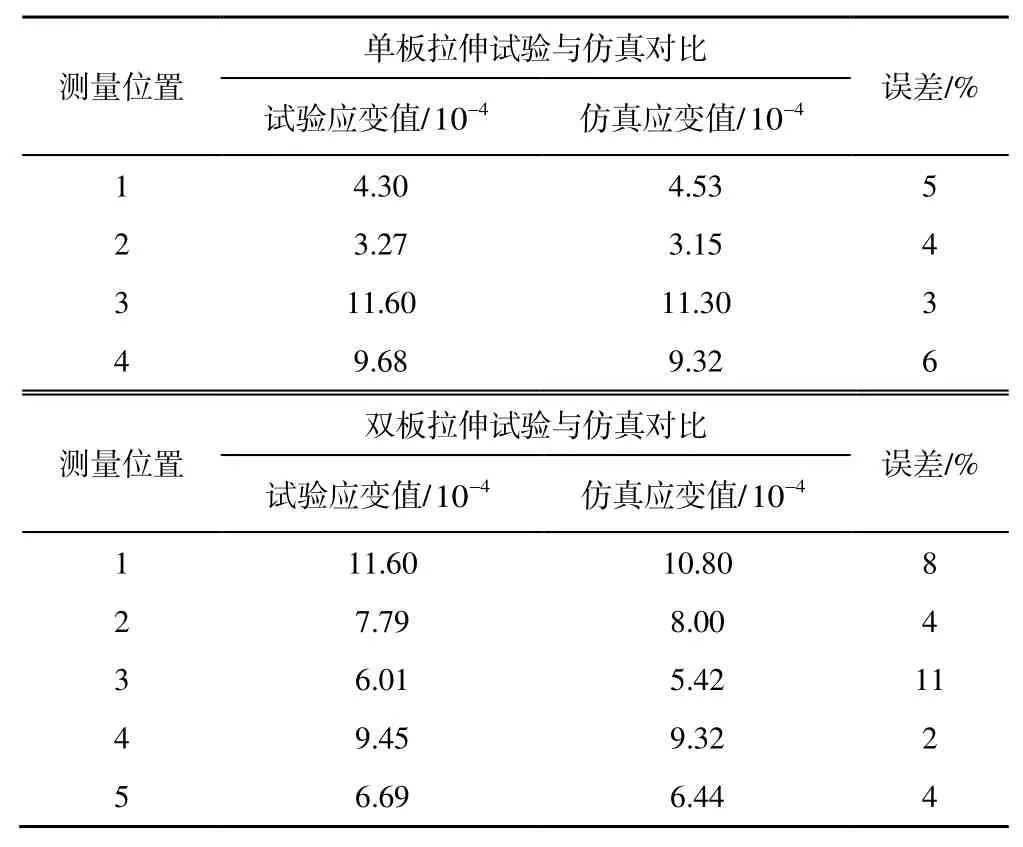
表4 试验测试与仿真结果对照Table 4 Comparison of test and simulation results

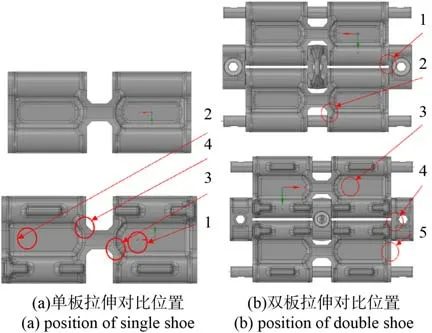
图8 试验与仿真比对位置示意图Fig. 8 Schematic diagram of comparison positions in test and simulation

1.3.2 单双板拉伸仿真结果分析

将连接部件与履带接触位置上的节点受力并进行求和，可以得到拉伸载荷下连接部件与履带的相互作用力的大小。由于连接部件上总拉力保持恒定，端联器与诱导齿受力大小之比也就是拉伸载荷分配比例。拉伸过程中的载荷分配如图9 所示，双块履带板拉伸过程中诱导齿承受41.3 kN 载荷，端联器承受34.7 kN 载荷，这与其连接工装上内部工装承受43.2 kN，外部工装承受32.8 kN 的载荷分布有所差异，说明载荷分配在履带的传递过程中发生了变化。同时上述载荷分配与单块拉伸板工装44.2 kN: 31.8 kN 的载荷分配同样有所差异，说明拉伸实验中履带板块数的增加影响到初始的载荷分配情况。在上下拉伸载荷不同的情况下，双块板拉伸试验中履带板会产生额外的弯矩，仿真中履带板中间位置处弯矩大小为38.8 N·m。

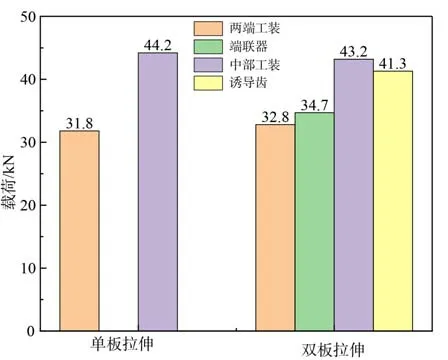
图9 工装与连接部件载荷分配Fig. 9 Load distribution between tooling and connecting parts

最大设计牵引载荷p作用下，单板与双板拉伸时的应力云图如图10、图11 所示，拉伸载荷作用下，单板双板拉伸试验履带板最大应力均出现在履带板加强筋拐角处，其最大应力分别为281 MPa与295 MPa，与单板拉伸相比，双板拉伸履带板由于载荷分配发生变化使得其最大应力提高，增长幅度约为4.5%，应力分布也与单板拉伸有所不同，端联器上载荷增加，使得外部加强筋上应力变大，在外部加强筋上出现了应力较大区域。双板拉伸与单板拉伸比较，其加强筋上载荷均有增加。

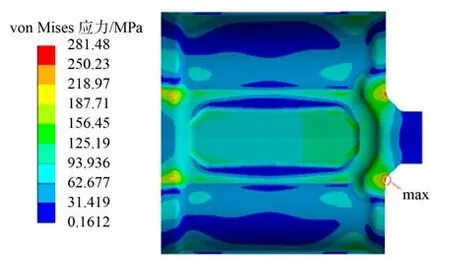
图10 单板拉伸应力云图Fig. 10 Tensile stress nephogram of single shoe

上述应力与载荷分配的差异表明履带板数目的增加对载荷分配产生了影响，进而影响到了履带板上应力分布。实际履带车辆上，单条履带履带板数目为60~100 块[19]，而履带板拉伸试验由于试验设施的限制(拉伸试验机长度，测量困难等原因)，拉伸的履带板块数有限，无法对多块板在拉伸载荷下载荷分配与应力分布进行测量。因此，有必要对多块履带板拉伸载荷与应力分布的方法进行研究。

2 多块履带板拉伸载荷分配计算方法研究

2.1 单板与双板试验与仿真结果分析

多块履带板承受拉伸载荷时简化示意图如 图12 所示。为了图12 中表达方便，将履带板上端联器与诱导齿简化为弹簧连接，诱导齿连接刚度为k1，端联器连接刚度为k2，履带连接部件上有F1的F2作用，而随着履带板拉伸载荷的传递，履带板上载荷分配发生变化，连接部件处载荷F1、F2分别变为与，…，，n为单圈履带环内任意一块履带板。运用圣维南原理分析可知，载荷分配的差异只会影响在小部分范围。随着载荷传递次数的增加，初始载荷分配F1、F2对后续载荷分配的影响逐渐减弱，当履带载荷传递足够多时，稳定的履带板载荷的分配应与连接部件的局部刚度呈正比，局部刚度越大，承受的载荷越大，而局部刚度与端联器、诱导齿刚度k1、k2，连接部件处履带销轴的刚度以及履带板体乃至橡胶衬套的刚度有关。

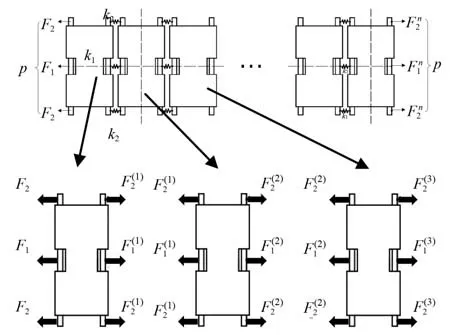
图12 多块履带板受拉伸载荷示意图Fig. 12 Schematic diagram of multiple track shoes under tensile load

拉伸载荷趋于稳定的载荷分配只与履带结构有关，因此只要计算的履带板数目足够多，就能够得到稳定的分配结果，而在有限元计算中将多块履带板全部建模并进行有限元方法计算效率过低，由于履带环上单块履带结构相同，因此可以用每一轮的载荷分配作为输入，利用迭代法对履带板载荷进行计算。

履带板迭代模型计算模型如图13 所示，单块履带右端连接部件施加对称约束，左端施加初始拉伸载荷，将履带载荷F1、F2以压力的形式作用在履带板左端的连接部件上，通过单块板的有限元计算得到下一块板的履带载荷分配F1′、F2′，并将右端对称面上各个节点的载荷重新分配至履带左端进行新一轮的有限元计算。其有限元迭代法计算过程(见图14)可分为如下3 个步骤。

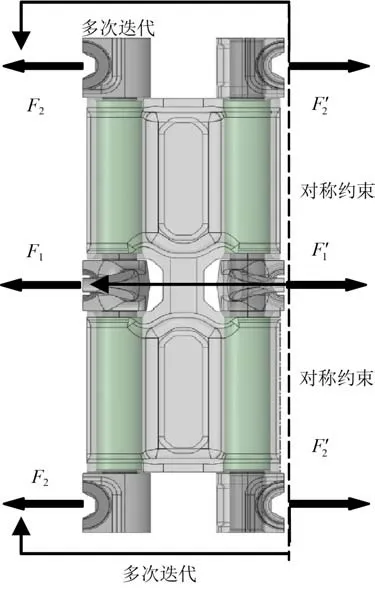
图13 履带板计算迭代模型Fig. 13 Iterative calculation model of track shoe

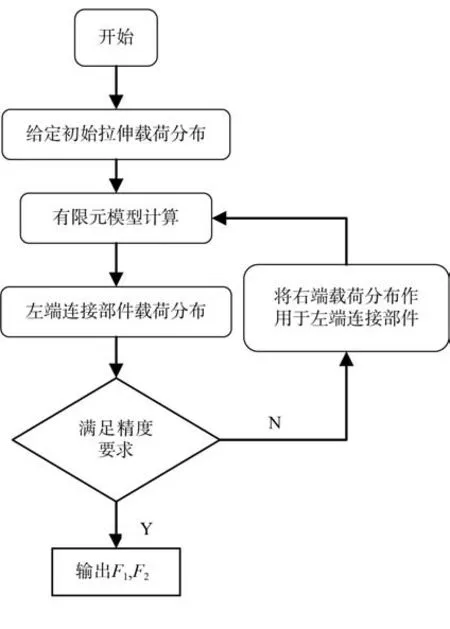
图14 有限元迭代法流程图Fig. 14 Flow chart of finite element iterative method

步骤1计算履带上整体拉伸载荷，为简单起见可以先将整体载荷平均分配在端联器与诱导齿上。

步骤2进行有限元计算，得到与履带板右端载荷分布F1′和F2′。

步骤3提取右端节点受力，将右端载荷分布F1′和F2′作为载荷输入至履带板左端连接部件进行有限元计算。

重复步骤2、步骤3，直至前后两次运算约束支反力之差满足精度要求，得到多板受拉伸载荷时结果。

2.2 有限元计算迭代结果

图15 为有限元迭代过程中诱导齿与端联器上载荷分配随迭代次数变化曲线，四种不同的初始载荷分配比例经过多轮的迭代计算后，诱导齿与端联器上的拉力数值逐渐趋于稳定值。迭代6 轮后诱导齿(一半模型)承受38.6 kN 载荷，端联器上承受37.9 kN 载荷。多板拉伸时，诱导齿与端联器的载荷分配比例为50.5%：24.75%：24.75%。该结果与2.3 节中单板拉伸时58%:21%:21%以及双板拉伸的54%:23%:23%载荷分配均有所差异。

图15 迭代过程中载荷分配变化曲线Fig. 15 Load distribution variation curves during iteration

多种不同的初始载荷分配比例经过迭代后拉伸载荷分配均趋向同一结果，表明多板载荷的分布只与履带板自身结构有关，利用有限元法进行迭代方法计算具有良好的鲁棒性。

2.3 两步法

2.2 节中对多块拉伸履带板载荷分配进行了讨论，当履带板数目足够多时，载荷分配比例会趋向一个定值，如图16 所示，第n块履带板与左右两块板拉力均相等时(n足够大)，由对称性可得，第n块板上连接部件与中间面上存在3 个对称面 1、2、3。由于拉伸载荷的作用，中间对称面2 与对称面1、3 之间的距离随着载荷增大而逐渐增大，但是仍然保持着对称面之间的互相平行。因此，在有限元计算方法中，可以通过试算加调整的方法进行载荷分配的计算。

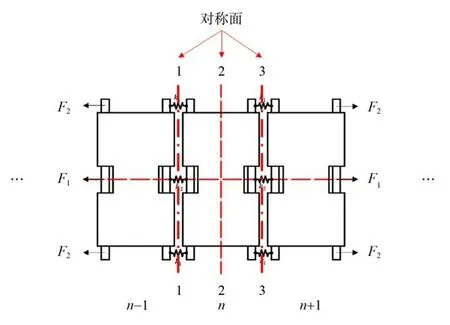
图16 多块履带板受拉伸载荷示意图Fig. 16 Schematic diagram of multiple track shoes under tensile load

如图17 所示，在有限元仿真中，可以将履带板一端设置为对称约束，而另一端施加固定拉伸方向位移a，以反映多块板受拉伸载荷时载荷分配趋于稳定的情况，通过试算合反力并进行调整使其达到所需施加的载荷，最终载荷分配比例可由各个连接部件上的合反力求得。

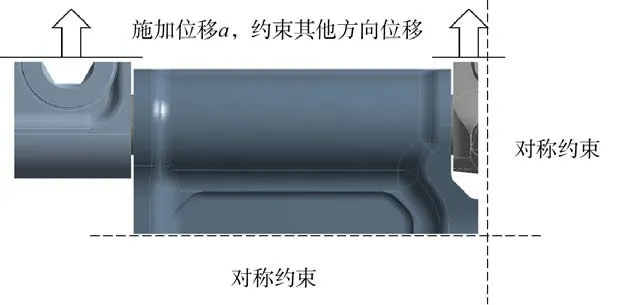
图17 试算方法有限元计算模型Fig. 17 Finite element calculation model of trial calculation method

当履带板结构受力较小时，几何非线性与材料非线性影响不明显，此时连接部件局部刚度k近似视为常数，因此合反力与位移有良好的线性关系，试算结果位移与合反力的关系如图18 所示，有限元计算中合反力与位移具有明显的线性关系，因此试算方法步骤可以分为：1)有限元计算得到该次条件下的合反力；2)进行等比例放缩便能得到所需载荷作用下履带板的载荷分配及应力结果。

图18 两步法位移与合反力关系Fig. 18 Relationship between displacement and total reaction force

如表5 所示，当对对称面施加固定位移时，诱导齿承受51%的载荷，端联器承受49%的载荷，这与迭代过程结果相同，因此两步法可以快速求得履带环上受拉伸载荷时稳定的载荷分布，继而对履带板强度进行进一步分析与计算。

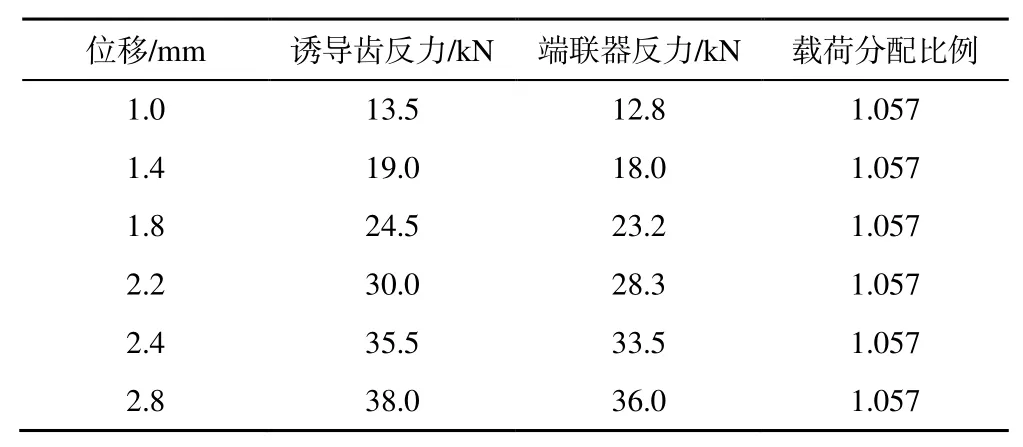
表5 不同位移下诱导齿与端联器载荷 分配比例Table 5 Load distribution ratio under different displacements

与有限元迭代计算相比，两步法忽略拉伸载荷随履带的传递过程，只关注履带稳定的载荷分布结果。当履带左右两端载荷大小相等时，其上对称面会随着载荷的增大而发生平移，如同绳索一样，这揭示了多板拉伸履带形变约束，将履带板形变与拉伸载荷分配联系起来，只需要进行施加位移便能够得到最终的载荷分配，通过有限元计算得到位移与拉伸载荷呈现良好的线性关系，因此运用两步法计算时只需要进行一步试算，再等比例放缩便能够得到相应拉伸载荷下履带板的应力结果，与迭代法进行5 次有限元计算才能收敛至最终结果相比，其过程更加便捷，并且在有限元计算中，施加位移会使得数值计算收敛性更好。

3 多板拉伸与单双板拉伸结果对比

第1 节试验与仿真表明不同块数的履带板受拉伸载荷时应力分布有所不同，而第2 节中得到诱导齿与端联器上稳定载荷分配与1.3 节中单板，双板拉伸载荷分配均有一定差异，在现有条件下，履带板强度的测定依然是通过对单板拉伸进行强度试验。因此，应该探明单板、双板拉伸试验与多板拉伸试验之间履带板应力分布的差异，以此来更好的进行履带板强度设计。

图19 为有限元迭代后稳定拉伸载荷作用下履带板应力云图，其上最大应力为330 MPa。单、双板拉伸状况最大应力(见图 9、图 10)分别为 281 MPa、294 MPa。多板迭代后应力最大值涨幅明显，较单板拉伸增加了17%，最大应力出现位置也发生变化，出现在外侧加强筋上。

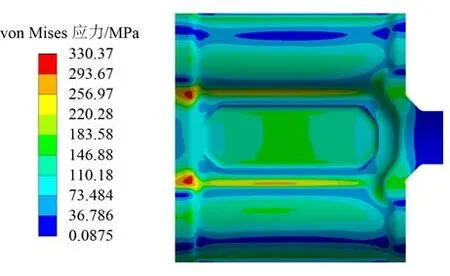
图19 多板拉伸应力云图Fig. 19 Multi-shoe tensile stress nephogram

履带销轴挠度过大会使得履带与主动轮啮合发生问题，因此履带销轴的最大挠度也是一个重要指标。通过仿真计算，双板与多板履带销轴挠度如 图20 所示，两者的最大挠度均出现在履带板接触段。多板拉伸迭代后履带销轴最大挠度明显大于双板拉伸时履带销轴挠度，端联器与诱导齿部分挠度也有差别。履带销轴的受力如图21 所示，q(x)为履带销轴所受载荷沿销轴分布，L为橡胶衬套段长度，当连接部件作用力F1、F2传递至履带销轴上时，拉伸载荷F1、F2的差异使得多板与双板拉伸挠度的不同。因此在设计计算中，不能忽略载荷分配对履带销轴最大挠度的影响。

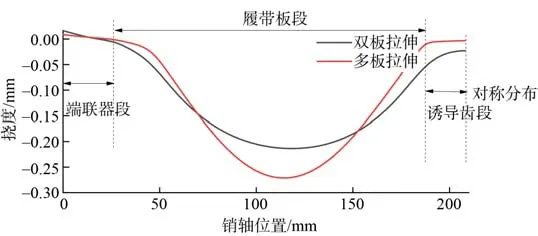
图20 履带销轴挠度对比Fig. 20 Comparison of track pin deflection

图21 履带销轴受力分析Fig.21 Force analysis of track pin shaft

在现有条件下，履带板强度的测定依然是通过对单板或者双板拉伸进行强度试验，而上述分析表明，单板双板履带板拉伸与多板履带拉伸的应力与挠度结果相差较大，基于单块与双块的履带板拉伸试验无法很好反映出履带环上各履带板在受拉伸载荷时实际的应力结果，在设计过程中，应对拉伸载荷的分配的影响加以考虑。

4 结论

本文对拉伸载荷下双销式履带板的载荷分配与结构强度进行了试验与仿真计算，得到以下主要结论：

1)由于双销式履带连接部件结构不同，履带板受拉伸载荷时载荷分配会随履带板数目的增加发生变化，多板拉伸时载荷分布只与履带板结构有关，而与初始载荷分配无关，多板拉伸下该型双销式履带板诱导齿与端联器载荷分配比例为2:1:1。

2)两步法利用履带受拉伸载荷时的特点进行计算，能够快速对履带板受拉伸载荷时最终的载荷分配结果进行计算，计算结果与迭代方法相同，因此具有良好的适用性。

3)履带强度试验普遍采用单块履带板进行拉伸，而仿真结果表明，多板拉伸与单板拉伸在应力分布与销轴挠度上均存在差别，因此后续强度试验中应该注意履带块数对强度分析的影响。