随机初值条件下基于翼伞的无人机回收方法

孙昊, 孙青林, 孙明玮, 陈增强

(南开大学 人工智能学院，天津 300350)

0 引言

翼伞回收系统由柔性翼伞伞衣和负载组成，并通过翼伞为系统提供升力[1]。相较于圆伞、盘缝带伞等传统伞降系统，翼伞不仅继承了传统伞降系统飞行稳定、负载能力强的优势，还可通过下拉翼伞后缘，控制其飞行方向，在物资精准空投、飞行器回收等领域具有不可替代的重要作用[2]。

早在1994 年美国军方就认识到了翼伞系统在飞行器回收及物资空投领域的巨大优势，提出了“二十一世纪陆军”计划与“下下一代陆军”(AAN)计划，在AAN 计划中将“先进的空投手段”列为首要的国防需求，并由Natick 实验室领导了名为“先进精确空投系统”(APADS)项目的研制任务[3]，在该任务中主要通过翼伞将军用物资精确地投放至战场中，特别适合缺乏可靠路基、海基着陆场的复杂地形。在此基础上，美国于2001年开始进行翼伞回收航天器及无人机的实验，如NASA 曾经采用一个689 m2的翼伞对X-38 无人飞行器进行回收[4-5]。此外，翼伞还应用于火箭助推器[6-7]等航天器及其组件的回收，更是在无人机回收领域受到了广泛关注。

然而，与其他刚体无飞行器相比，翼伞采用翼伞提供升力。伞衣的特征面积较大，在空中易受外界风场干扰，且存在柔性形变及强非线性动力学特征，导致该系统的精确建模与轨迹跟踪控制的难度更大。针对该问题，目前已有大量学者进行了相关研究。如Lü 等[8]和Zhao 等[9]建立了翼伞的多体动力学模型，并进行了相关仿真实验。Nie 等[10]根据Robin-Neumann 转换矩阵对充气状态下的翼伞伞衣进行了数值模拟。Zhang 等[11]则采用流-固耦合技术，模拟了风场环境下的翼伞动力学特性。Li 等[12]研究了一种基于飞行数据的新型翼伞系统建模方法，并与实际飞行实验进行了对照。Yang 等[13]采用涡格法(VLM)和工程估算法相结合的方法，基于小扰动假设建立了考虑伞衣附加质量的6 自由度线性模型。而针对翼伞的控制方面，同样有大量学者进行了相关研究，Tanaka 等[14]采用稳定控制的方法实现了动力翼伞的纵向控制，通过推力装置控制其飞行高度。Slegers 等[15]通过最小二乘法辨识无动力翼伞的气动参数，并采用模型预测控制实现轨迹跟踪，在飞行试验中轨迹跟踪的误差约为 50 m。在文献[15]的基础上，Rogers 等[16]基于大规模并行计算的方法，探索了翼伞的鲁棒归航控制。Chen 等[17]基于一种虚拟结构编队的引导策略，实现了翼伞的精确归航。高峰等[18]和Gao 等[19]则针对翼伞的归航分为5 个阶段，探索了翼伞的分段归航，并对翼伞回收系统的动态进行了建模分析。通过对已有研究的分析，可以看出相较于刚性无人机，翼伞的非线性特征更加明显，柔性伞衣的柔性特性更强。并且在实际飞行测试中翼伞回收系统的开伞位置不确定，无法确定系统归航控制中的初值条件，其回收精度和轨迹跟踪精度仍有较大的提升空间，轨迹跟踪误差在几十米范围内。因此，采用人类进行辅助仍是实现翼伞回收精确归航的主要手段[20]。

针对上述问题，本文基于翼伞系统的无人机回收进行了研究。首先，基于翼伞与所回收负载的运动约束，建立翼伞回收系统的动力学模型，并基于实际飞行数据调整该模型中伞体及负载的气动参数，为实际飞行实验提供仿真实验环境。随后，基于自抗扰控制技术设计翼伞水平控制器，对回收系统的偏航角进行精确控制。自抗扰控制可通过扩张状态观测器将包含外界未知风场在内的总扰动视为一个整体，并对外界总扰动进行针对性补偿，并以此控制翼伞的飞行方向。最后，通过大量实际回收实验对所提出的算法进行了验证，在飞行测试中所回收负载的实际落点与目标点的平均误差为 21.6 m，可实现无人机的精确回收。

1 翼伞回收系统动力学建模

翼伞回收系统由柔性翼伞伞衣与负载两部分组成，如图1(a)所示。伞衣负责提供升力，负载包含运输物、控制模块等。翼伞分为有动力和无动力两类，动力翼伞在负载后部添加了一个动力装置，如推进器、螺旋桨等。同时翼伞可通过系统舵机拉动控制绳，令伞衣后缘下偏，改变伞体的升气动特性，实现水平方向控制。在建模中，翼伞回收系统及其参考坐标系的示意图如图1(b)所示。

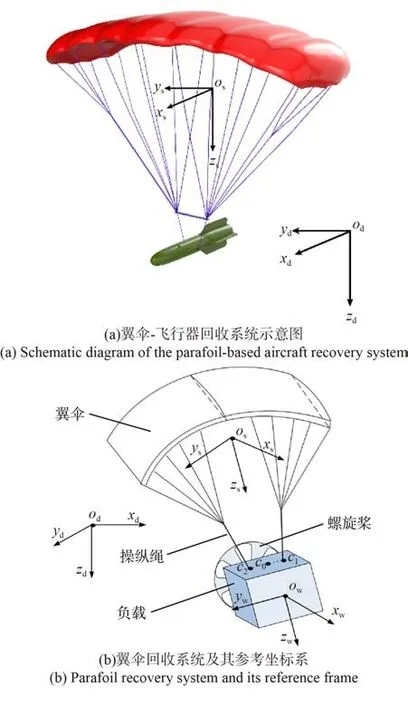
图1 翼伞回收系统Fig. 1 Schematic diagram of the parafoil recovery system

首先，在本文的动力学建模中，需进行以下假设[21]：

1)在翼伞伞衣完全张开后，假设伞体形状不变；

2)伞体的质心与伞体气动力中心位置相同，但是与翼伞系统的重心不相同；

3)忽略负载的升力，仅考虑负载的气动阻力。

其次，本文主要有3个坐标轴，分别为大地坐标系(惯性坐标系)Odxdydzd、翼伞坐标系Osxsyszs和负载坐标系Owxwywzw。其中，大地坐标系的原点dO为空间中的不动点，这里一般设定为系统初始点或目标点，ddO z轴垂直向下，ddO x轴与ddO z轴垂直，朝向正东方，ddO y轴朝向正北方。翼伞坐标系原点为伞体质心，ssO z轴指向图1(b)中的C0点，ssO y轴指向伞体右侧，ssO x轴指向伞体正前方。负载坐标系原点为负载质心，wwO z轴指向负载正下方，Owyw轴指向负载右侧，Owxw轴指向负载正前方。

首先，在建模中翼伞系统的伞衣与负载的受力可表示为

式中：下标s 和w 分别表示伞体和负载的变量；上标aero、G、f、t 分别表示系统的空气动力、重力、伞绳的拉力、摩擦力、负载的推力；P和H表示动量矩阵和动量矩矩阵；ω为系统的角速度矩阵；v为系统的速度矩阵；F和M分别表示受力和力矩；为伞体气动力，受安装角、攻角和伞衣后缘下偏等多个因素影响。伞衣后缘下偏将导致气动力变化，控制偏航角，其气动力可表示为

式中：fm表示乘积因子，取值1.24；ρ表示空气密度；fS表示每个分片的面积；LfC和DfC分别表示伞衣后缘的升力系数和阻力系数；[ufvfwf]表示伞衣后缘的速度。

伞衣后缘的升力系数和阻力系数可表示为

式中：LαC为升力斜率；ε为伞体下反角；0α为零升力迎角；kAr为翼伞展弦比系数，Ar表示翼伞的展弦比；Df0C为翼型阻力；δ为伞衣结构系数；cα可表示为

α为攻角，fα为下偏量，即为翼伞系统控制量，rα为安装角。

负载和伞体的动量与动量矩可表示为

式中：[vw,ωw]和[vs,ωs]分别表示系统在负载及伞体坐标系下的速度和角速度；aA和rA分别表示伞体的附加及真实质量矩阵；wm表示负载的质量；Jw表示负载的转动惯量；A1~A4将质量矩阵分解为4 个4×4 的矩阵。

在式(1)、式(2)中，悬挂绳和控制绳上的拉力是一对作用于负载和伞体上的作用力与反作用力，可表示为

式中：w-sT表示由负载坐标系到伞体坐标系的转换矩阵。

如图1 所示，由于所回收负载与伞体通过悬挂绳相连，这两部分的速度和角速度约束可表示为

式中：w-cL表示由负载重心到点mC的位置向量；Ls-c表示由伞体重心到点Cm的位置向量。

同时，所回收负载与伞体之间的欧拉角限制可表示为

此外，基于式(1)、式(2)及式(10)，负载与伞体间受力的约束可表示为

式(13)代入式(1)，可得

基于(8)式、(9)式，式(14)可表示为

式(15)中伞绳作用于翼伞伞衣与负载上的拉力为一组作用力与反作用力，这组力被视为连接翼伞与负载上受力的“纽带”。如式(15)所示，拉力将在模型约束推导中直接抵消，因此本文在建模中无需关注拉力的具体数值，但需要假设舵机提供的拉力可在较短时间内将伞绳拉至控制量指定的位置，并且在选型时确保硬件可实现伞绳快速 下拉。

结合以上各式，即可得到翼伞回收系统的动力学模型，本文的翼伞模型为8 自由度，系统状态为。该动力学模型的状态更新矩阵可写为

式中：1E~4E、1F~4F均由系统模型推导得出。部分详细推导过程可参考文献[21]。

2 自抗扰控制器的设计

本文将基于自抗扰控制技术，设计翼伞回收系统的水平控制器，实现翼伞回收系统的精确归航，确保系统的落点位于目标位置。自抗扰控制技术由韩京清[22]提出，目前已有大量学者针对各种系统进行了相关研究[23-24]。如图2所示，本文所述翼伞系统的柔性伞衣的非线性强，可通过自抗扰控制理论中的扩张状态观测器将其扩张为一个总扰动，并进行针对性补偿，提高系统的控制精度。图2中，z1、z2、z3分别为系统状态x1、x2、x3的观测值，r1为系统目标偏航角。

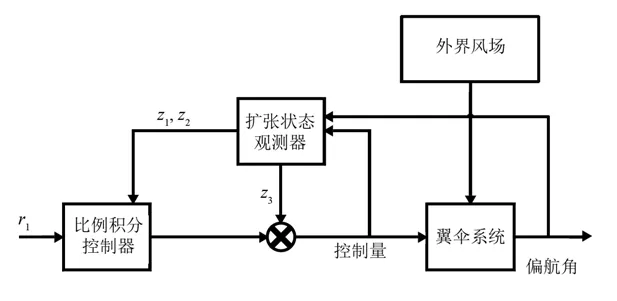
图2 自抗扰控制器Fig. 2 Active disturbance rejection controller

由于翼伞本身是一个欠驱动系统，唯一的控制量是伞衣后缘下偏。由于翼伞的控制量仅能控制翼伞的偏航角，翼伞俯仰角的控制则一般需要采用非常规的控制手段，如大幅度改变安装角，或引入辅助设备，如引导伞、伞衣开孔或扰流板等。因此，本文将主要针对翼伞偏航角通道的控制进行研究。

翼伞系统的偏航角状态可表示为

式中：f表示包含外界扰动以及内部不确定性在内的系统总扰动；dtrw表示包含外界扰动；b表示控制增益；u为系统控制量，即为fa。

基于式(18)，可建立系统的扩张状态观测器：

类似地，式(18)可重写为

式中：D=[ 0 ,0,1]T。

定义ei(t) =xi(t) -zi(t)，系统的观测误差可表示为。结合式(19)与式(21)，可得

在式(22)中，矩阵L必须满足：

式中：wo表示扩张状态观测器的带宽；l1=3wo；。

最后，自抗扰控制器的控制量可表示为

在翼伞系统的归航控制中，系统的参考输入可表示为

式中：(yd，xd)表示目标点的水平坐标位置。通过这种设计，可确保翼伞回收系统可从任意位置飞向目标点，实现无人机的精确回收。

基于以上各式，式(17)可重写为

由式(27)可以看出，自抗扰控制器可将非线性的翼伞回收系统的总扰动视为是一个扩张状态，这个状态可以被扩张状态观测器进行动态地观察和补偿，将其近似地看作一个线性系统，降低其控制难度并提高其控制精度。

3 仿真与飞行实验

3.1 实验环境

基于第1、2 节所述内容，本文将采用仿真实验和飞行测试方法，对所提出的建模与无人机回收方法进行系统性验证。

图3 给出了本文所设计的嵌入式控制器与翼伞回收系统。在仿真实验中，嵌入式控制器将通过串口设备与模型相连，最大限度地模拟系统的真实运动状态。在进行大量仿真验证后，本文基于该翼伞回收系统进行飞行测试，验证翼伞回收系统的落点精度。如图4 所示，系统将首先采用动力装置进行爬升，待系统到达指定空域后，进行自主归航，并最终实现精确着陆。本文所用翼伞回收系统的伞体面积为3 m2，负载质量为4.2 kg，飞行状态下的系统平均水平速度为4.5 m/s，垂直速度为2.2 m/s，最小转弯半径约为17 m。

图3 嵌入式控制器及翼伞回收系统Fig. 3 Embedded controller and parafoil recovery system

图4 归航控制流程Fig.4 Homing control process

3.2 仿真实验

针对所建立的气动模型进行仿真验证。在本文的建模中，重点在于确保翼伞系统的水平速度、垂直速度以及最小转弯半径等可量化的运动状态与实际系统一致，便于调节控制器参数。本文的气动参数设计为CDf0=0.35、CLα=0.7、kAr=1.25、ε=0.26。

针对模型验证的仿真结果如图5所示，在仿真的前20 s系统为无控制量状态，20 s后控制量为最大值。系统的飞行速度如图5(d)所示，水平速度和垂直速度与实际系统相符。此外，如图5(a)所示，在最大控制量下，系统的最小转弯半径为17.5 m，证明所建立的动力学模型可为飞行实验调整控制器参数。

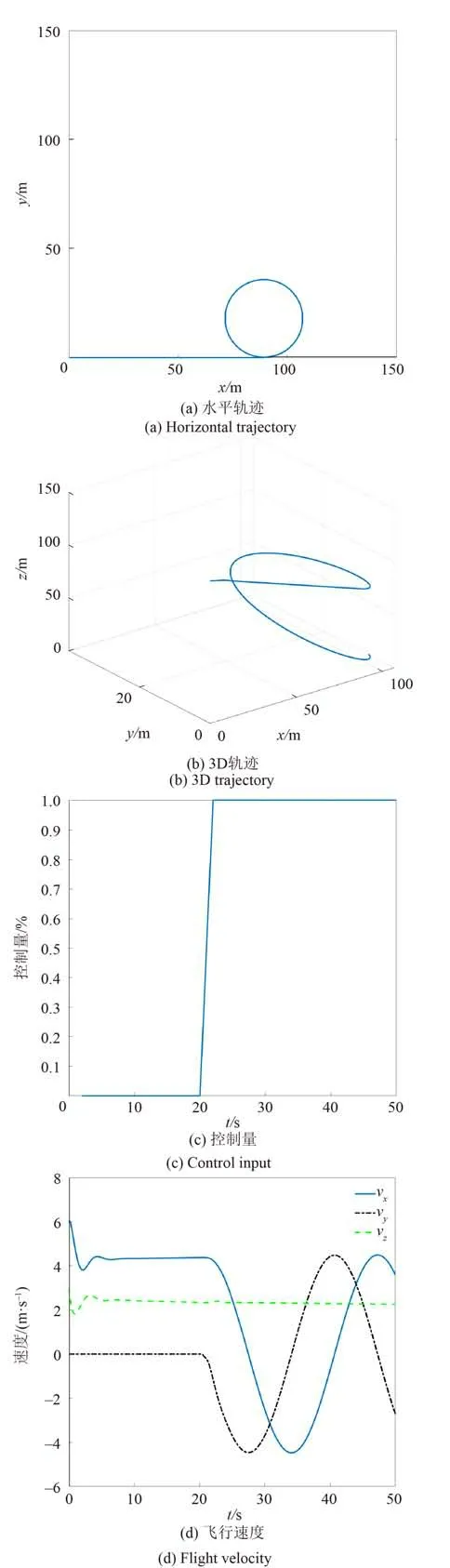
图5 模型验证Fig. 5 Model verification

基于本文所建模型，本节给出3 种不同环境下的翼伞回收系统的归航实验，以及基于规划轨迹的归航实验实例。实验1 目标点的坐标为[150 m, 150 m, 0 m]，初始点为[0 m, 0 m, 125 m]，系统的初始偏航角为0°，实验结果如图6 所示，可以看出自抗扰控制器系统可实现翼伞回收系统的精确归航，所回收负载的水平着陆误差仅为4.7 m。

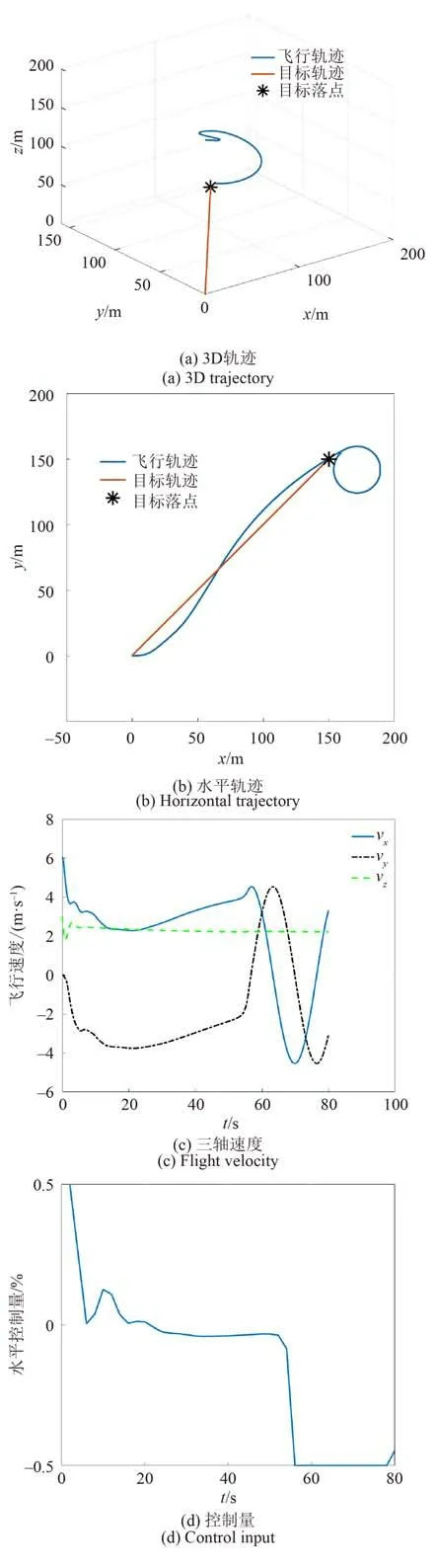
图6 仿真实例1Fig. 6 Simulation case 1

实验2 目标点的水平坐标为[-150 m, -150 m, 0 m]，初始点为[0 m, 0 m, 110 m]，系统的初始偏航角维持不变，实验结果如图7 所示。在仿真实验中，系统在初始阶段存在较大的偏航角误差，如 图7(d)所示，其控制量可针对这种状态进行快速反应，最终落点误差为10.3 m。

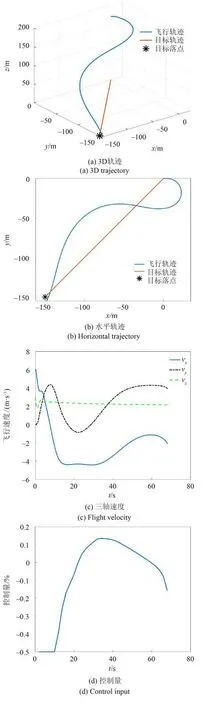
图7 仿真实例2Fig. 7 Simulation case 2

实验3 目标点的水平坐标为[-150 m, 150 m, 0 m]，初始点为[0 m, 0 m, 170 m]，系统的初始偏航 角为0°，实验结果如图8 所示。此外，为进一步验证系统的鲁棒性，在实验3 中还加入外界风场的干扰，外界风场速度为2 m/s，方向为x轴正方向。由图8(d)可以看出，在风场环境下系统的控制量存在一定波动，但在60 s 内，系统可恢复稳定，最终落点误差为3.7 m。

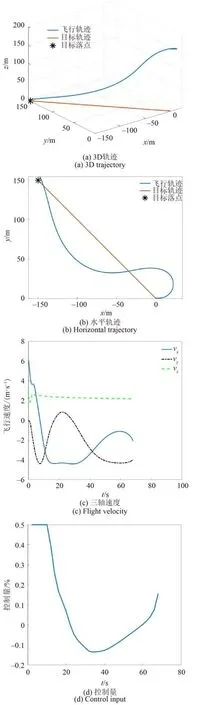
图8 仿真实例3Fig. 8 Simulation case 3

实验4 目标点的水平坐标为[0 m, 0 m, 0 m]，初始点为[470 m, -230 m, 500 m]，系统的初始偏航 角为0°。本文基于3 自由度模型，采用高斯伪谱法进行轨迹规划，并将其在x轴、y轴处的位置转化为时间t的函数，将其作为系统的参考输入，最后采用8 自由度动力学模型进行轨迹跟踪。在建立3 自由度模型的过程中，考虑了水平控制量对系统 水平速度和垂直速度的影响。由于翼伞实际控制量伞衣后缘下偏会提高伞体向前的阻力面积，降低水平飞行速度，同时由于该操纵同时降低了伞体内部的充气体积，下降速度将会提高。根据上述规律，本文在模型中将水平控制对飞行速度的影响进行了线性化处理，6 自由度模型可表示为

式中：φ为系统偏航角；vxy为系统水平速度；vz为系统垂直速度；为系统风场速度；u1为系统控制量，本文中 -1 ≤u1≤1；k1为水平控制量对水平速度的影响系数，本文中为；k2为水平控制量对垂直速度的影响系数，本文中为。在本文的3 自由度模型中，翼伞系统的唯一控制量u1为翼伞系统的偏航角速度。在8 自由度模型的仿真中，系统的稳定水平速度为4.5 m/s，稳定垂直速度为2.2 m/s。同时，如图5(a)所示，最小转弯半径为17.5 m。针对上述8 自由度动力学模型的飞行状态，本文建立了翼伞的6 自由度模型，其控制量为零时的水平速度与垂直速度与8 自由度模型一致，设定vxy=4.5 m/s，vz=2.2 m/s。同时，为了保证模型间最小转弯半径一致，在3 自由度模型中系统的最高角速度被设为0.14 rad/s。

轨迹跟踪的实验结果如图9 所示。在实验4中，翼伞所跟踪的目标轨迹由高斯伪谱法计算得出，实验结果证明通过对目标轨迹进行跟踪可有效消耗赘余高度，降低落点误差。

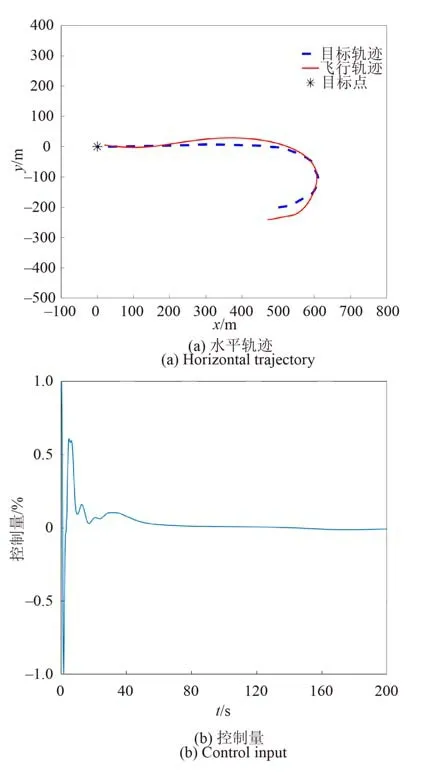
图9 仿真实例4Fig. 9 Simulation case 4

由于翼伞系统在投放后的飞行时间由初始高度决定，飞行时间固定，必须在固定时间到达目标位置。控制器虽然可以保证翼伞的轨迹跟踪误差在一定时间内收敛，但该系统在仿真中受外界环境风扰、系统的非线性动力学约束等干扰，无法保证在某个时刻翼伞的跟踪误差为0 m，这也是数值仿真中翼伞落点出现误差的最主要原因。而如何最小化翼伞的落点误差是翼伞归航控制研究的核心问题，也是未来的重要研究方向。

3.3 飞行测试结果

如图4 所示，本文在仿真实验基础上进行飞行测试。为验证本文所提出模型及控制器，在飞行测试中的自抗扰控制器控制参数与仿真中完全一致，控制器参数设定为p0.29=k、d1.08=k、o3.2=w。共进行了15 次飞行试验，具体实验结果如表1 所示，15 次飞行测试的平均落点误差小于30 m。部分飞行测试结果如图10 所示，可以看出本文所设计算法可实现翼伞回收系统的精确归航，所回收的无人机被精确地投放至目标区域。通过自抗扰控制技术，系统的飞行轨迹平滑，控制量稳定，可满足无人机精确回收的需要。

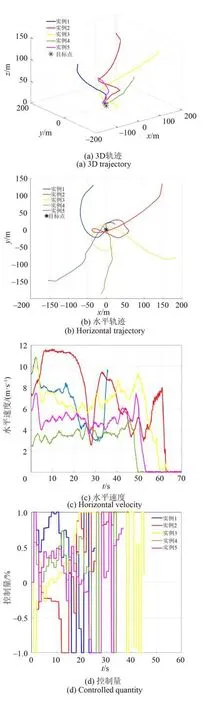
图10 飞行测试结果Fig. 10 Flight test results

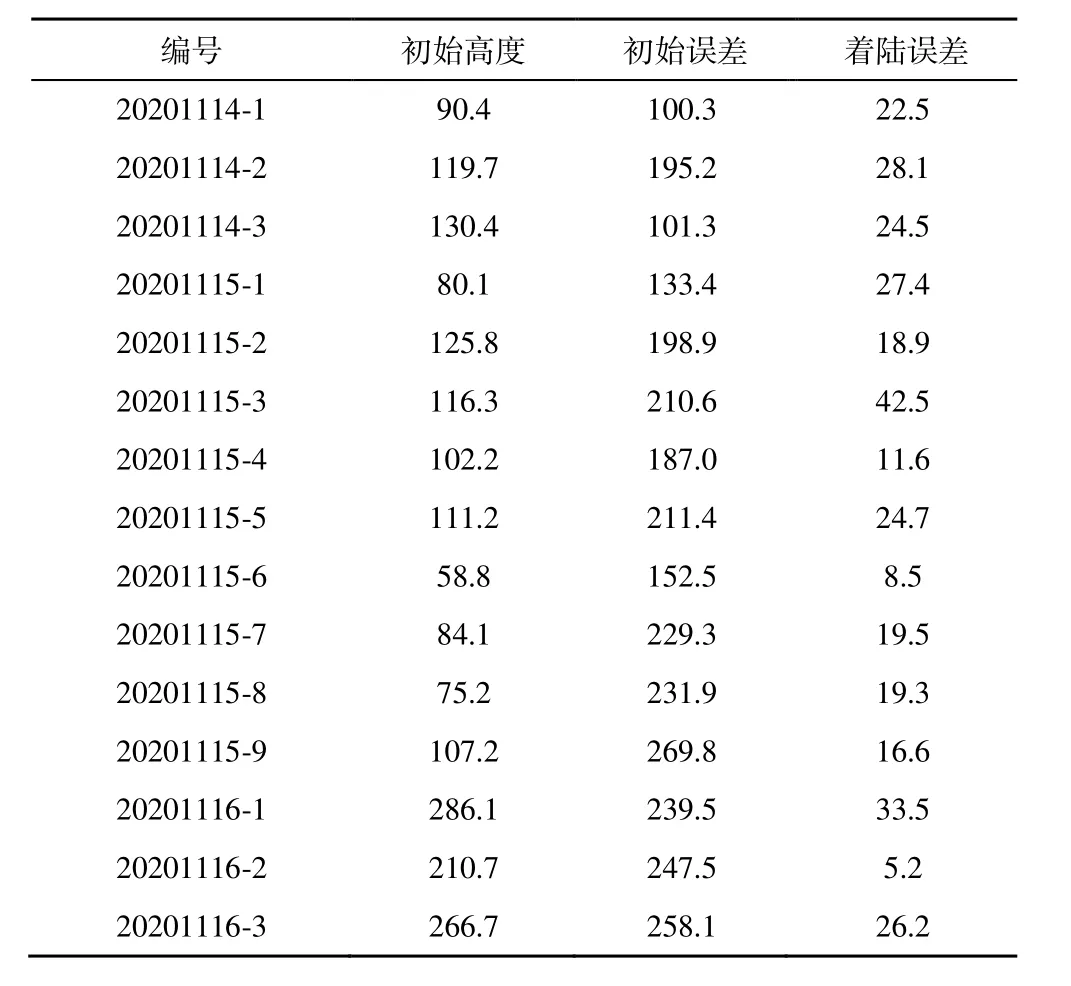
表1 飞行实验结果Table 1 Flight test results m

4 结论

为实现无人机的精确回收，本文采用自抗扰控制技术，研究一种翼伞回收系统的归航控制方法。基于翼伞系统飞行稳定、方向可控、可雀降着陆的优势，可将无人机精确地运送至指定目标区域。首先，本文通过分析翼伞伞体和负载的相对运动，建立了翼伞的简化动力学模型，为实际应用和控制器参数调试提供理指导。随后，基于自抗扰控制器对外界干扰进行精确补偿，精确控制系统的飞行方向，实现翼伞系统的精准归航。从实际飞行测试中可以看出，该算法所设计的战场精确物资空投系统可实现无人机的精准回收，平均落点误差为21.9 m。