时间步长和无量纲壁面距离y+对实尺度船舶数值模拟的影响

陈昆鹏，张青山，杜云龙

(上海船舶运输科学研究所有限公司 航运技术与安全国家重点实验室， 上海 200135)

0 引 言

目前，最常用的船舶有效功率预测方法有模型尺度的拖曳水池试验和模型尺度的数值模拟2种。然而，在模型尺度下通常只能满足模型与实船的弗劳德数相同,不能满足雷诺数相同，因此实尺度船舶数值模拟方法是目前国内外学者研究的热点[1]。CASTRO等[2]采用壁面函数和沙粒粗糙度对KCS集装箱船进行了实尺度自航数值模拟。DEMIREL等[3]提出了一种基于非稳态雷诺平均纳维-斯托克斯(Reynolds-Averaged Navier-Stokes,RANS)的计算流体动力学(Computational Fluid Dynamics,CFD)模拟方法，该数值模拟方法能预测船用涂料和生物污底对船舶阻力的影响，并考虑粗糙度对实尺度KCS船数值模拟结果的影响，从而得出船舶的阻力和有效功率。张立等[4]对标准模型尺度船舶开展了CFD多维度仿真，得到了不同维度下的计算结果，复合航次试验结果表明，网格密度、无量纲壁面距离y+和湍流模型对计算结果有很大影响。邵文勃等[5]基于CFD技术对滑行艇的静水阻力进行了计算，分析了时间步长和近壁面网格划分对计算精度的影响，数值模拟结果表明，时间步长和y+发生变化主要影响的是滑行艇的摩擦阻力和艇底表面的气液分布，数值计算结果与模型试验结果能较好地吻合。胡海洲[6]开展了毂帽鳍和舵附推力鳍的实尺度节能效果研究，其y+设置在30～500范围内。NIKLAS等[7]将y+设置在30～200范围内,对实尺度船舶开展了耐波性研究。

RANS方法通过壁面函数控制近壁面处的流体流动，近壁面处第一层网格的高度用y+表示[4]。在隐式非定常模拟中，时间步长往往取决于流动特性，而与库朗数无关。为得到合理的计算结果，应根据模拟特征采用不同的时间步长。文献[1]提出,在实尺度船舶阻力性能模拟中，目前普遍采用的时间步长范围为0.005Lpp/U～0.010Lpp/U(Lpp为船舶垂线间长;U为船舶航速)。本文以某23万载重吨散货船为研究对象,根据其特点，结合船长和航速选取时间步长，建立不同的近壁面网格，以舯部为参考点读取y+值，开展实尺度船舶阻力数值模拟研究，分析时间步长和近壁面网格划分对计算精度的影响。

1 数值方法

本文的控制方程为RANS方程和连续方程，满足质量守恒和动量守恒。

1) 所有流动问题都要满足质量守恒定律，该定律可表述为：单位时间内流体微元体中质量的增加等于同一时间内流入该微元体的净质量。根据该定律,可得出质量守恒方程为

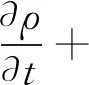
(1)

在笛卡尔坐标系中，式(1)可表示为

(2)

对于不可压缩流体，其密度为常数,有

(3)

式(1)～式(3)中:ρ为流体密度;t为时间;v为速度矢量;u、v和w为速度矢量在x、y和z方向的分量。质量守恒方程亦称作连续方程。

2) 所有流动问题都要满足动量守恒定律，该定律可表述为：微元体中流体的动量对时间的变化率等于外界作用在该微元体上的各种力之和。动量守恒方程(又称纳维-斯托克斯方程)为

(4)

(5)

(6)

式(4)～式(6):Su=Fx+sx;Sv=Fy+sy;Sw=Fz+sz;μ为流体的动力黏度。Fx、Fy和Fz为微元体上的体力;对于黏性为常数的不可压缩流体,sx、sy和sz为0。

雷诺平均方法又称RANS方法,其核心是不直接求解瞬时的纳维-斯托克斯方程，而是在时均化的方程中通过某种模型将瞬态的脉动量体现出来。

关于湍流脉动值的雷诺应力项属于新的变量，为使RANS方程封闭，本文采用两方程涡黏模型可实现的k-ε(k为紊流脉动动能;ε为紊流脉动动量的耗散率)湍流模型。

采用VOF(Volume Of Fluid)方法捕捉自由液面，该方法通过研究网格单元中流体和网格体积分数确定和追踪自由液面。若水的体积分数为1，则该网格单元全部充满水；若水的体积分数为0，则该网格单元为空气；若水的体积分数在(0,1)范围内，则该网格单元为交界面。

由于船体壁面附近存在较大的速度梯度，只有划分高质量的边界层网格才能求解近壁面的流场信息。与模型尺度数值模拟相比，实尺度船舶数值模拟中的边界层相对较薄，第一层边界层对计算精度有重要影响，其厚度通常用y+表示。

y+的表达式为

y+=(yuτ)/ν

(7)

式(7)中:y为该点到壁面的距离;ν为流体的运动黏性系数;uτ为壁面摩擦速度。[8]

2 计算域与网格划分

数值模拟中的计算域为立方体，与模型尺度不同，实尺度船舶的计算域相对较大，长、宽和高分别约为3 330 m、860 m和1 210 m，船首距离边界超过4倍船长，船尾距离边界超过5倍船长，船体到侧边界的距离和水深均超过2.5倍船长。由于船体是左右对称的，可计算半船，船体中纵剖面所在面为对称面。在计算域边界中，顶部、底部和远离船体的侧面为滑移壁面，入口设置为速度入口，出口设置为压力出口。图1为数值模拟中的计算域。

图1 数值模拟中的计算域

网格采用非结构化网格;船体附近的网格设置得较为密集;对船首、船尾和水线面的网格作加密处理；远离船体位置的网格设置得较为稀疏。通过建立矩形等加密区域控制体网格局部加密，对船体附近、艏艉和水线面网格进行局部加密，可平衡计算资源与网格精细度。图2为船体附近网格划分情况。

a) 船体附近网格

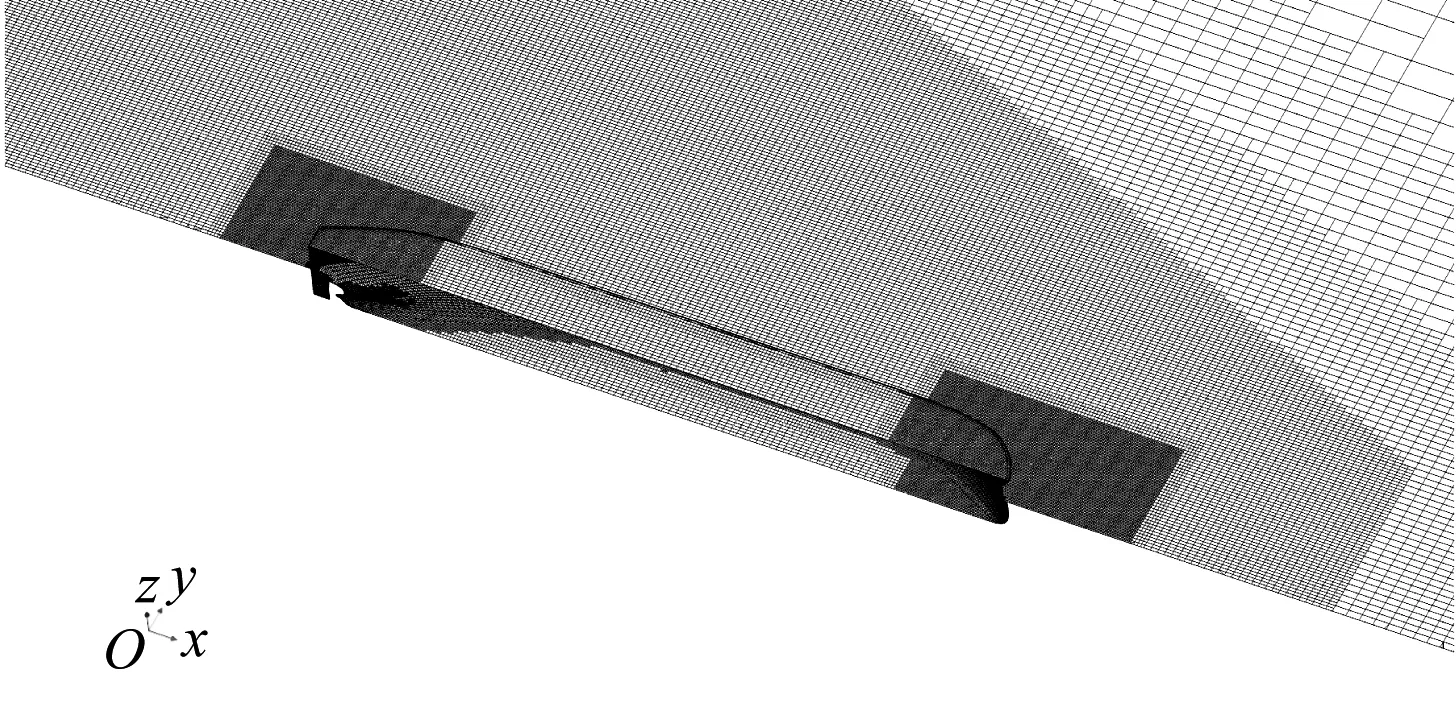
b) 自由液面区域网格加密

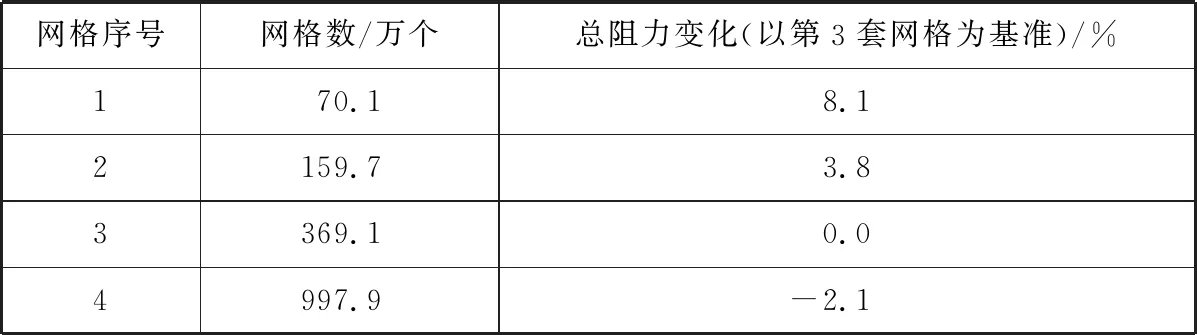
表1 网格无关性验证结果

由表1可知,最密集的第4套网格与第3套网格的差距为-2.1%，因此选取第3套网格进行数值模拟。

3 计算工况

在实尺度船舶阻力性能模拟中，目前普遍采用的时间步长范围为0.005Lpp/U～0.010Lpp/U[1]，当该船的垂线间长为314.6 m，航速为14.5 kn时，其时间步长范围为0.211～0.316 s。为研究时间步长对实尺度数值模拟结果的影响，在设计航速下从小到大设置若干个时间步长，其范围包含文献[1]中的0.005Lpp/U～0.010Lpp/U，本文的时间步长最小为0.000 24Lpp/U(0.010 s)，最大为0.015 00Lpp/U(0.633 s)，表2为数值模拟中不同工况下的时间步长。

为研究y+对实尺度船舶数值模拟结果的影响，在设计航速下从小到大设置若干个边界层厚度和层数。船体不同位置的y+值不同，因此统一取平行中体舯部作为参考点。根据时间步长的数值模拟结果，以时间步长0.080 s为例开展y+对比计算。

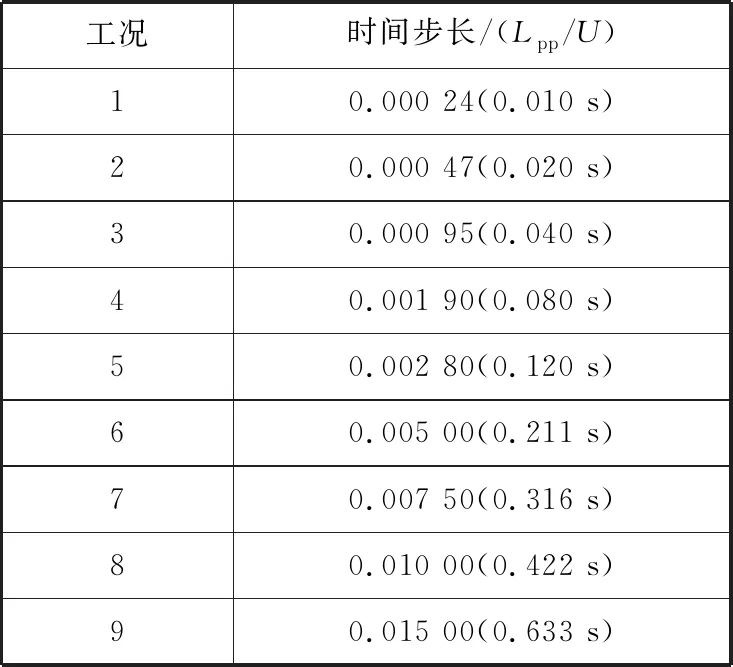
表2 数值模拟中不同工况下的时间步长

在对时间步长进行对比研究时，近壁面网格、y+和其他参数不变;在对y+进行对比研究时，时间步长和其他参数不变。表3为数值模拟中不同工况下的y+。

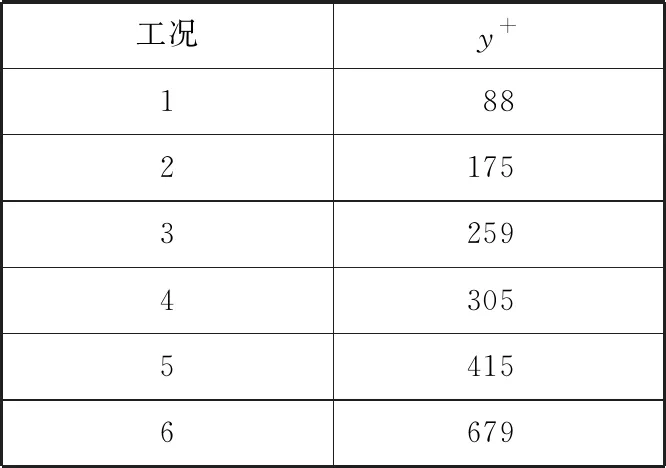
表3 数值模拟中不同工况下的y+

4 数值模拟结果分析

表4为通过水池模型试验预报的14.5 kn航速下的实船阻力Rt和有效功率Pe。试验在上海船舶运输科学研究所有限公司的船模拖曳水池内进行，船模长7.3 m，水池长192 m，宽10 m，水深4.2 m。根据以往的预报结果，该船模拖曳水池试验预报结果与实船试航结果的吻合性较好，因此通过模型试验预报的实船阻力和有效功率可作为实尺度船舶数值模拟对比验证的依据。

表4 通过水池模型试验预报的14.5 kn航速下的实船阻力Rt和有效功率Pe

当控制变量为时间步长时，其对数值模拟结果的影响见表5。

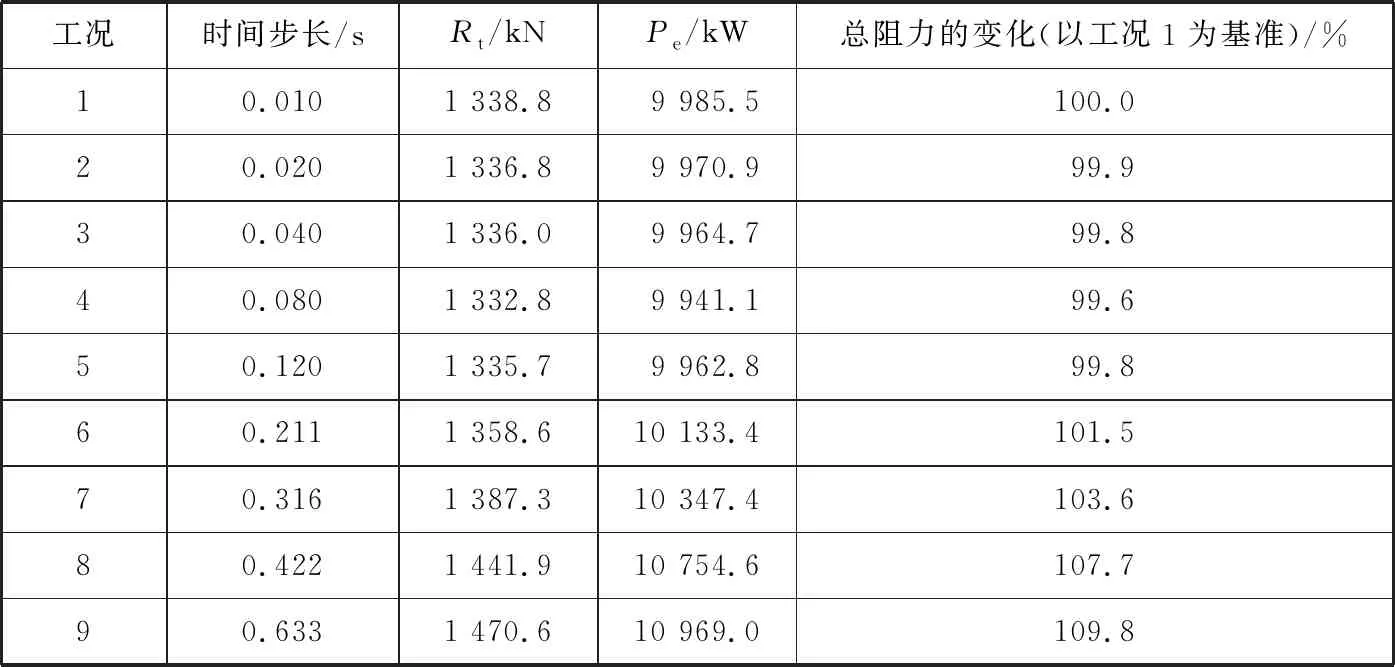
表5 时间步长对数值模拟结果的影响

图3为总阻力随时间步长的变化趋势。从图3和表5中可看出:当时间步长小于0.211 s(即小于0.005 00Lpp/U)时，阻力和有效功率随时间步长的变化在1.5%以内;当时间步长大于0.211 s时,阻力和有效功率随时间步长的增加大幅度上升;当时间步长为0.422 s(即0.010 00Lpp/U)时,通过数值模拟得到的阻力相比作为基准的时间步长为0.010 s(即0.000 24Lpp/U)时的阻力数值模拟结果增加7.7%。

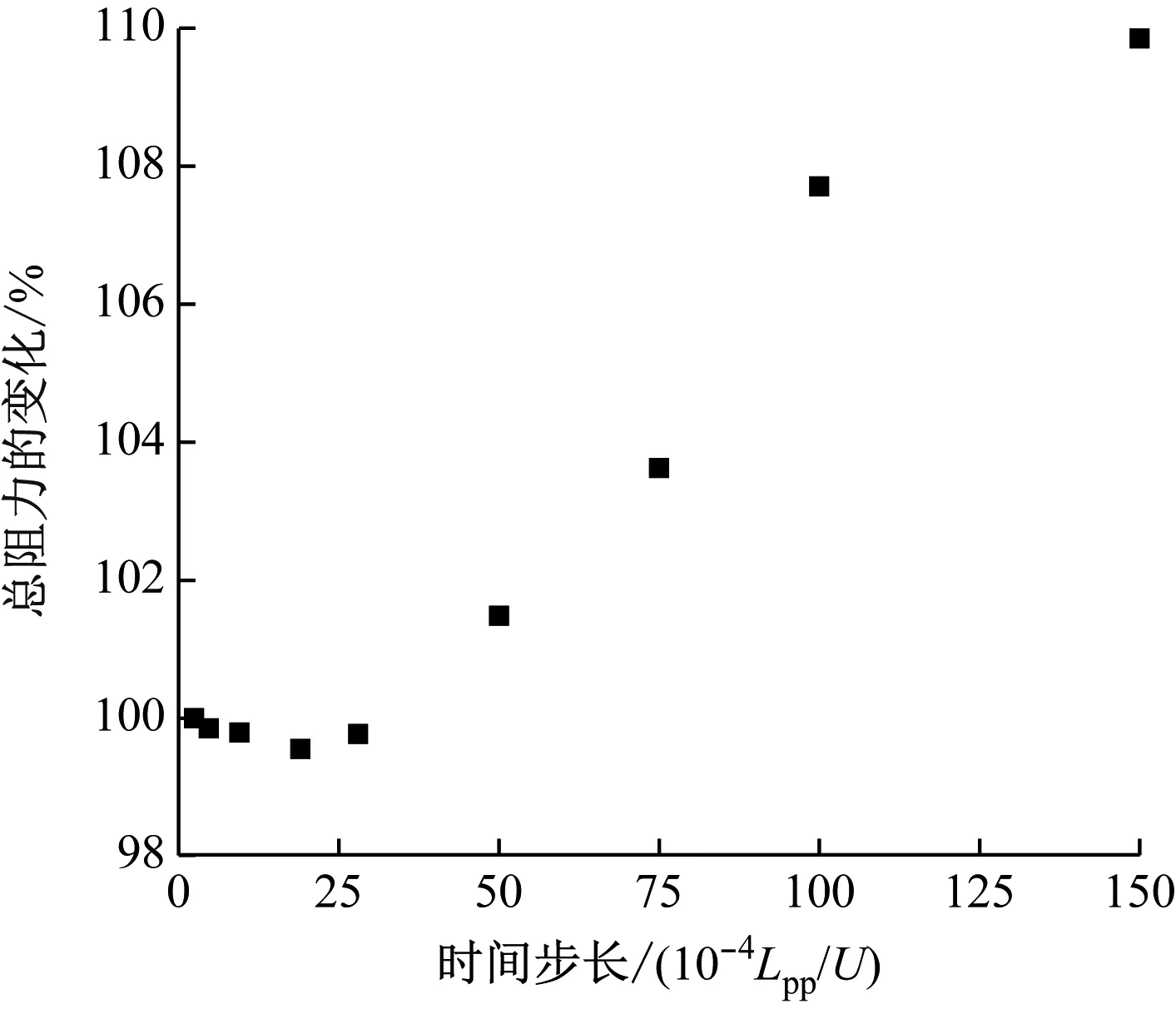
图3 总阻力随时间步长的变化趋势

当时间步长为0.010～0.211 s(即0.000 24Lpp/U～0.005 00Lpp/U)时,宏观总阻力变化幅度有限，但通过数值模拟得到的流场细节随时间步长的增加而有损失。图4为自由液面随时间步长的变化趋势，颜色表示自由液面高度在大地坐标系下的变化。在网格和其他参数完全相同的情况下，当时间步长为0.211 s(即0.005 00Lpp/U)和0.316 s(即0.007 50Lpp/U)时,很多波形细节完全消失，且自由液面出现不真实的异常锯齿状。

a) 时间步长为0.010 s

b) 时间步长为0.080 s

c) 时间步长为0.211 s

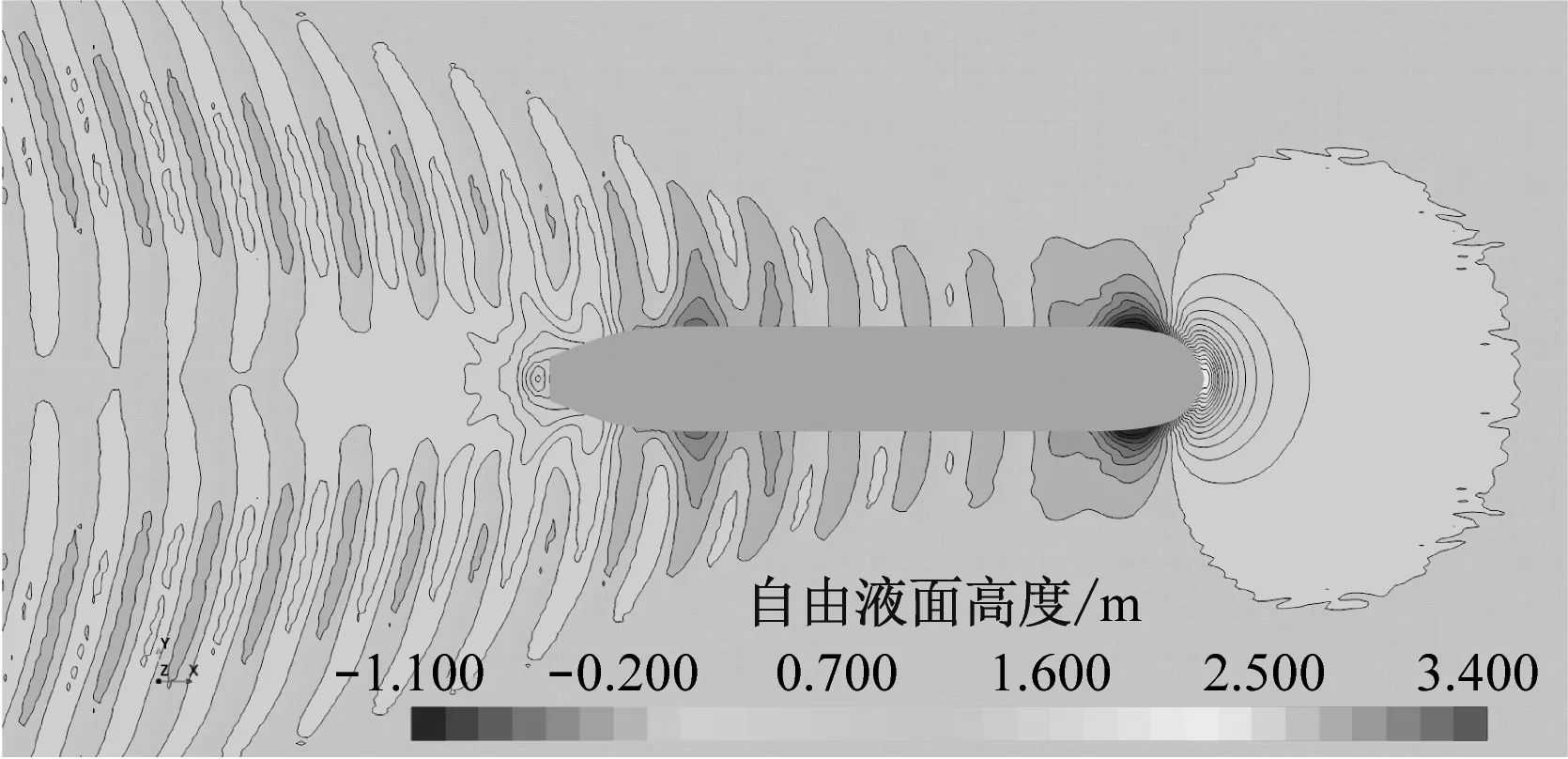
d) 时间步长为0.316 s

在网格和计算机资源相同的条件下，时间步长与数值模拟计算的时间成本呈线性关系，时间步长越小,数值计算的时间成本越高。综合考虑计算速度和精度，认为类似的肥大型船的时间步长应取0.002Lpp/U～0.005Lpp/U,对应本文所述船舶0.08～0.21 s，时间步长0.005Lpp/U～0.010Lpp/U对于本船来说过大。

表6为y+对总阻力数值模拟结果的影响;图5为总阻力随y+的变化趋势。由表6和图5可知:当y+的值在88～679范围内时,通过数值模拟得到的阻力和有效功率随y+的增加而增大;当y+值增加到679时,阻力值相比y+=175时的阻力值增加2.3%;当y+从175增大到415时,阻力值增大2%;当y+从175减小到88时,阻力值减小2.5%。

此次数值模拟的对象为实船，其雷诺数远大于模型，对数律区域较大，因此没有必要将y+控制在50～60，对于本文所述船舶和类似船型而言，y+在175～679范围内取何值理论上都是合理的，当舯部y+=679时,艏部会出现y+>679的区域，因此认为该船通过近壁面网格设置的舯部y+应为约415。

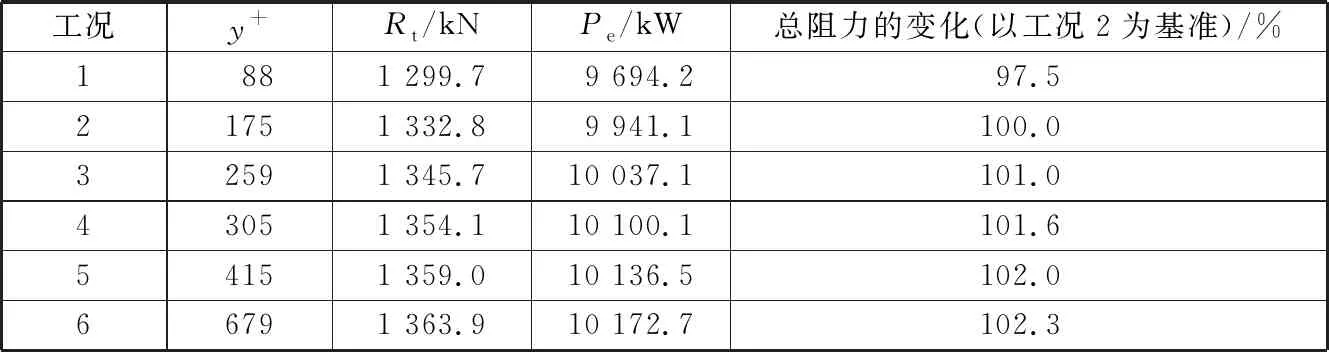
表6 y+对总阻力数值模拟结果的影响

该船在y+=415，时间步长为0.08 s时的数值计算结果与模型预报结果相差3%，有较好的流场细节。

图6为舯部参考点y+=259时的全船y+分布，艏部和艉部因速度变化较大,产生了1个艏部y+大于参考点y+的区域和1个艉部y+小于参考点y+的区域，船体大部分区域的y+都与参考点y+接近。

当时间步长为0.010～0.211 s，y+在175～305范围内时，相比时间步长，实船数值模拟中的总阻力和有效功率对y+更敏感，时间步长变化21倍对总阻力的影响与y+变化1.74倍相近。当时间步长在0.211～0.633 s范围内时，实船数值模拟中的总阻力对时间步长更敏感，总阻力随时间步长的最大变化幅度为9.8%。

5 结 语

本文以RANS方程和连续方程为控制方程，采用有限体积法进行空间离散，在控制时间步长和y+等参数的情况下建立了某23万载重吨散货船的实尺度船舶阻力数值模拟计算模型，重点研究了时间步长和y+值对计算精度的影响。结果显示：在较大范围内,时间步长和y+对阻力计算结果的影响显著，最大达9.8%，在一定范围内影响不超过2%;当舯部y+为200～420，时间步长取0.002Lpp/U～0.005Lpp/U时，合理设置时间步长和y+可相对准确地开展实尺度数值模拟，预报船舶的静水阻力性能和有效功率。研究成果可供类似船舶开展实尺度船舶快速性数值模拟研究参考。