“程”风破浪

何晓明

一元二次方程的应用是初中数学的重难点内容之一，也是中考的重点考查对象. 很多同学会发现，解一元二次方程并不难，然而一旦它与实际问题结合起来，有的时候就无处下手，找不到等量关系. 今天我们一起探讨一下“一元二次方程的实际应用”问题.

[考点提炼]

考点1：一元二次方程与利润问题

例1 某商场将进货价为30元的台灯以40元售出，平均每月能售出600个. 调查发现，售价在40元至60元范围内时，这种台灯的售价每上涨1元，其销售量就将减少10个. 为了实现平均每月10 000元的销售利润，这种台灯的售价应定为多少？这时应购进台灯多少个？

解题思路：找到等量关系是破解一元二次方程的关键所在. 本题中，等量关系为：总利润 = 每件商品的利润[×]销售数量，可以设每个台灯涨价x元，则每个台灯的利润为（40 + x - 30）元，台灯销售数量为（600 - 10x）个，根据题意，列方程为（40 + x - 30）（600 - 10x） = 10 000，解方程即可.

易错点：没有根据问题的实际意义检验方程的根是否符合题意. 如此题方程的两个解为x1 = 10，x2 = 40，题目中要求售價在40元至60元范围内，当x2 = 40时，售价为40 + 40 = 80（元），不符合题意，应该舍去.

解题要点：1. 找到等量关系；2. 检验根的合理性.

考点2：一元二次方程与增长（下降）率问题

例2 某公司2022年10月的营业额为2500万元，按计划第四季度的总营业额要达到9100万元，求该公司 11月和12月两个月营业额的月均增长率.

解题思路：本题中等量关系为：10月的营业额 + 11月的营业额 + 12月的营业额 = 第四季度的总营业额. 设该公司11月和12月两个月营业额的平均月增长率为x，则11月的营业额为2500（1 + x），12月的营业额为2500（1 + x）2，根据题意，列方程为：2500 + 2500（1 + x） + 2500（1 + x）2 = 9100，解方程即可.

易错点：1. 不能正确表示出12月的营业额；2. 审题不仔细，将第四季度主观臆断为12月.

解题要点：明确变化率问题的等量关系. 设a为基础量，x为平均增长（下降）率，n为增长（下降）次数，b为增长（下降）后的量，则a（1 ± x）n = b.

考点3：一元二次方程与几何图形结合的实际问题（如与几何图形结合的面积问题、动点问题等）

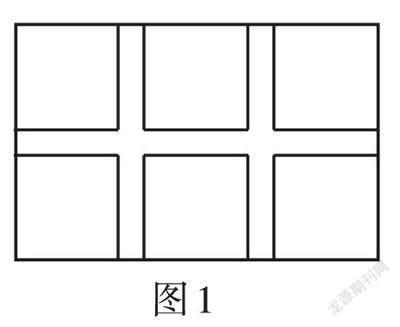
例3 如图1，在一块长92 m、宽60 m的矩形耕地上挖三条水渠（水渠的宽都相等），水渠把耕地分成面积均为885 m的6个矩形小块，水渠应挖多宽？

解题思路：在几何图形的面积问题中，利用面积公式列出等量关系是解决此类问题的常用方法. 本题设小路的宽为x m，根据题意，得（92 - 2x）（60 - x） = 885 [×] 6，求解即可.

易错点：1. 等量关系找得不好，导致列不出方程或者列出的方程很复杂；2. 没有根据问题的实际意义检验方程的根是否为实际问题的解.

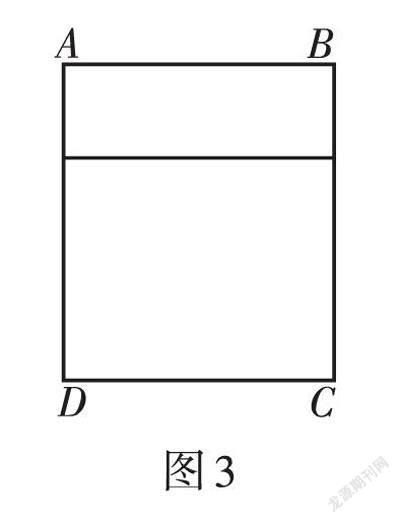
解题要点：如图2，利用平移的方法将6块矩形耕地拼成一个大矩形，再利用面积公式列方程.

[真题精讲]

点评：解题关键是用一个未知数表示出长和宽，然后利用面积公式来列出一元二次方程.

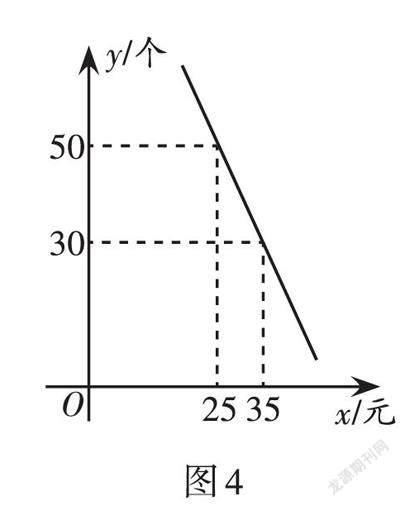
例5 （2022·辽宁·盘锦）某商场新进一批拼装玩具，进价为每个10元，在销售过程中发现，日销售量y（个）与销售单价x（元）之间满足如图4所示的一次函数关系.

（1）求y与x的函数关系式（不要求写出自变量x的取值范围）；

（2）若该玩具某天的销售利润是600元，则当天玩具的销售单价是多少元？

分析：（1）直接用待定系数法，求出一次函数的关系式；（2）根据题意，设当天玩具的销售单价是x元，然后列出一元二次方程，解方程即可求出答案.

解：（1）一次函数的关系式为y =  - 2x + 100（过程略）；

（2）根据题意，设当天玩具的销售单价是x元，

由题意得（x - 10）（ - 2x + 100） = 600，解得x1 = 40，x2 = 20，

∴当天玩具的销售单价是40元或20元.

点评：解题关键是理解题意，正确找出题目中的等量关系，列出方程或函数关系式.

[总结提升]

通过对2022年各地区中考中一元二次方程应用题的分析，我们发现试题普遍关注合理设置实际问题情境，突出对考生列方程与解决实际问题能力的考查，同时关注社会热点，体现素养立意. 下面分享几点解决此类问题的经验.

（一）回归教材，重视基础

综观近年来各地区的此类考题，很多试题都源自教材例题、习题，或者是由教材例题、习题经过改编的变式拓展题. 因此，在平时的学习中，一定要重视教材的例题、习题.

（二）抓住关键，找好等量

要认真阅读题目，分析题意，并能分解题目，各个击破，从而找到已知的条件和未知问题. 必要时可以通过画图、列表等方法来帮助我们理顺已知与未知之间的关系，找到一个或几个相等的式子，从而列出方程求解，同时还要及时检验答案的正确性并作答.

（三）规范答题，养成习惯

1. 写答案前，需先写“解”；2. 严格按照“设、列、解、验、答”的步骤书写答案，避免漏写步骤；3. 求得方程的两个根后，务必检验，看是否符合题意，舍去不符合题意的根；4. 结尾处，勿忘作答.

（四）优化解法，准确计算

要结合方程特点，选取合适的解题方法，如增长率问题可以优先考虑直接开平方法. 另外，设不同的未知量，方程的计算量也有差别，比如例1中的利润问题，若设台灯的定价为x元，计算量就会增加很多.

（五）关注生活，发展能力

一些试题背景设计往往会结合当代热点和时代潮流，因此我们应把重点放在如何分析和思考实际问题中的数量关系上. 例如，从关键字句中发现等量关系；发掘所涉及的基本数量关系，以此沟通不同量之间的关系；注意变化中的不变量，寻找隐含的等量关系.

如今，命题形式愈加多样化，知识交汇融合较多，例如一元二次方程常和函数结合，将问题设计成两问或三问，主要考查模型思想和分析问题、解决问题的能力，我们不必追求分类（如销售问题、循环问题等）硬套题型，而是应该多积累数学经验，不断提升解决问题的能力.