基于鸡兔同笼前测资源积累活动经验
文|徐丹燕
如何在《鸡兔同笼》学习中将学生已有的画图、列表等技能性经验转化为归纳、类比、推理等思维性经验?我们可以从学生的前测出发设计本节课。
一、前测回顾,呈现作品
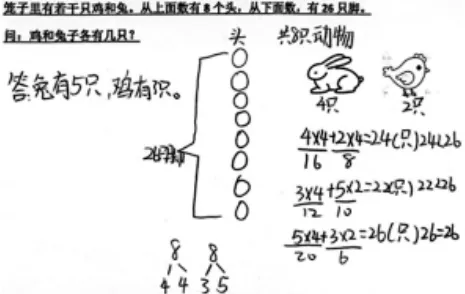
1.任务回顾:笼子里有若干只鸡和兔。从上面数有8 个头,从下面数有26只脚。问:鸡和兔各有几只?
2.呈现学生典型作品。如画图法、列表法、算式等。

①

②

3○
4○

5○
二、方法解读,多维对比
1.任务驱动
想:你能看懂这些方法吗?
评:选一种你最喜欢的方法,然后说明你看懂了什么?
(可以在练习纸上写一写、画一画)
说:最后把你的想法分享给同桌听一听。
2.方法评价
(1)教师可引导学生从方法入手,进行有序反馈。
(2)聚焦尝试法:图①中每个算式表示什么意思?你能不能结合图形来说一说?
(3)联通列举法:图②是怎么想的?兔子和鸡的个数是怎么变化的?哪一种方法和这种方法比较类似?
(4)重视调整法:图④为什么先从鸡兔各4 只开始试?这样做有什么好处?
(5)突破假设法:操作演示说明。
摆一摆:根据图⑤的过程可以用小棒演示,如图⑥。

⑥
说一说:结合图⑥重点解释疑难关键点“2”是什么意思?把兔子看成了鸡,脚就少了,这时候就需要用鸡去换兔,补一只兔比一只鸡多两只脚。
找一找:观察图⑤中左图与右边列式之间的联系,数形结合理解算理,图示表征假设法的笔算过程。
想一想:发现还可以全部先假设成兔。(五步列式:4×8=32,32-26=6,4-2=2,6÷2=3,8-3=5)学生结合算式再用小棒来演示五步算式的图示表征过程。
3.对比整理
思考:刚才通过对各种解答方法的分析,请你想一想,这些方法之间有什么相同点和不同点?学生发现它们的相同点是:都是利用了假设法。先假设,再调整。不同点是:假设的方法不同,有些是从最小量(最大量)进行假设,有些直接从中间量开始假设。
对比:你最喜欢哪一种方法?说说你喜欢的理由。
完善:请对原来的方法进行修改,让同学们看起来更明白。
小结:我们是如何来解决这个问题的?尝试法凭直觉,列举法很直观,操作法很形象,但它们都需要用到假设法进行推理,最终都可以通过“假设——比较——发现差异——找出差异存在的原因——调整”这一过程来解决。
像这样借助鸡兔同笼前测资源,组织学生对不同学习水平典型意义表征结果的剖析,进一步了解答题操作或思考过程,从而更好地促进学生亲身经历将实际问题抽象为数学模型并进行解释与应用的过程。

