脆性岩石多裂纹扩展的复合型相场模型研究
赵晨臣,饶秋华,易威,罗三
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 贵州路桥集团有限公司 贵州黔航交通工程有限公司,贵州 贵阳 550018)
在隧道开挖、边坡支护等岩体工程中,天然岩体内部存在的多裂隙受到地应力和工作荷载的作用后易发生起裂、扩展与贯通,存在岩体工程安全隐患问题[1-2],因此,研究岩石多裂纹扩展演变过程及其机理具有重要的理论与实际意义。由于理论上难以得到多裂纹起裂、扩展与贯通至破坏全过程的解析解,实验也难以实时检测复杂荷载条件下多裂纹扩展轨迹,因此数值模拟成为分析岩石多裂纹扩展与贯通机理的重要手段。数值方法主要包括连续方法(如传统有限元法[3]、边界元法[4]等)和非连续方法(如离散元法[5-8]、不连续变形分析[9]、流形法[10-11]等),前者通常需要在裂纹尖端建立复杂的奇异单元,后者通常需要通过材料有限的宏观力学参数来精确标定大量的细观参数、算法较为复杂。BOURDIN 等[12]提出一种新型连续介质方法—相场模型,通过引入相场变量φ代替新萌生的裂纹,基于变分原理[13]和Griffiths 断裂理论[14]建立相场控制方程,使得在模拟计算过程时无需显式地追踪裂纹面,而是通过相场变量的自动演化获取裂纹路径及位置。因此,相场模型在处理三维以及多裂纹问题上具有收敛性好、计算简便等优点,已经成为研究断裂问题的重要方法之一。由于经典的相场模型未区分正、负弹性应变能,拉、压应力将产生相同的应变能来驱动裂纹,从而在受压时产生不真实的裂纹[15]。为模拟复杂加载条件下的裂纹扩展,AMOR 等[16-17]分别基于球/偏、拉/压应变能分解提出了2 种改进的相场模型,但两者均未考虑拉伸(I 型)和剪切(II 型)裂纹扩展的区别。因此,ZHANG 等[18]基于F-准则[19](修正的G准则)和Miehe 应变能分解方法,提出了拉/压应变能分解的复合型相场模型,模拟分析了复杂加载条件下脆性岩石翼裂纹和次生裂纹扩展。ZHUANG 等[20]采用该复合型模型开展了复杂加载条件下类岩石闭合裂纹扩展模拟分析。借鉴ZHANG 的思路,采用AMOR 的应变能分解方法,可建立球/偏应变能分解的复合型相场模型,但该模型应用偏少,且这2种复合型相场模型的差异性和适用范围缺乏比较研究。目前,求解相场控制方程主要有整体算法和交错算法[21],交错法因比整体法更能有效地表征复杂裂纹的渐进性扩展全过程,且具有更高的收敛性而得到更广泛的应用。本文采用交错法[22],通过自编ABAQUS 的子程序UMAT 和HETVAL,建立基于拉/压应变能分解和球/偏应变能分解的2 种复合型相场模型数值求解方法,用于模拟脆性岩石双裂纹扩展与贯通轨迹并进行比较分析;通过开展不同中心间距下含双平行裂纹的红砂岩试件单轴压缩试验,分析多裂纹扩展行为及机理,并与模拟结果对比,验证2种复合型相场模型的有效性并阐明其异同性及适用范围。
1 基于交错法的复合型相场模型数值求解
1.1 基本相场模型
BOURDIN于2000年基于断裂变分模型建立了含相场变量φ的势能函数:
式中:相场变量φ=0 表示材料完好;φ=1 表示材料断裂;l表示裂纹弥散宽度(图1),l=27EGC/(512σ2t);E和σt分别为材料的弹性模量和抗拉强度。

图1 相场变量φ表示的弥散裂纹Fig. 1 A discrete crack in terms of a phase field φ
利用最小势能原理,便可通过式(1)得到经典的相场模型的控制方程(平衡方程和相场演化方程):
经典相场模型由总弹性应变能ψe控制相场变量φ的演化,即驱动裂纹扩展。由于ψe对于应力和应变区分不了正负,拉应力和压应力将产生相同的应变能来驱动裂纹,从而在受压时产生不真实的裂纹。
为了弥补经典相场模型的不足,Amor和Miehe分别于2009 年和2010 年提出了2 种不同的应变能分解方法对相场演化方程进行改进:Amor 提出将总弹性应变能ψe分解为拉伸(ψve+),压缩(ψve-)球应变能和偏应变能(ψde),认为压缩球应变能ψve-不能驱动裂纹扩展。
式中:κ是体积弹性模量;I是n阶单位矩阵;n为空间维数。
Miehe 提出将总弹性应变能ψe分解为拉伸(ψ+e)和压缩(ψ-e)应变能,认为只有拉伸应变能ψ+e才能驱动裂纹扩展。
式中:η是一个数值参数(0<η<<1),以避免当φ=1时计算不收敛;λ和μ是拉梅常数;运算符号 的定义为 x ±(x±|x|)/2;tr()表示矩阵求迹运算。同时,为避免卸载后弹性应变能释放而导致裂纹愈合,引入了一个历史场变量H表示从开始时刻(t=0)加载到任意t时刻在位置x处的最大驱动裂纹扩展的弹性应变能[13],以替代式(3)中的总弹性应变能ψe,得到改进后的相场演化方程:
其中Amor 提出的球/偏应变能分解和Miehe 提出的拉/压应变能分解所对应的历史场变量H分别为:
由于式(6)H和Gc均未考虑I型、II型裂纹扩展机理的不同,即未区分I 型、II 型的历史场变量(HI,HII)和临界能量释放率(GIC,GIIC),并认为GC=GIC,导致上述2 种改进的相场模型只能模拟任意加载条件下I 型裂纹扩展,而不能模拟II 型裂纹扩展。
1.2 复合型相场模型
为了准确模拟复杂加载条件下I 型、II 型裂纹扩展,ZHANG 等[18]于2017 年基于F-准则[19]和Miehe 拉、压应变能分解方法,考虑区分I 型和II 型的历史场变量(HI,HII)和临界能量释放率(GIC,GIIC),即采用HI/GIC+HII/GIIC替代公式(6)中的2H/GC,建立了拉/压应变能分解的复合型相场模型:
同理,本文基于ZHANG 的相场控制方程以及Amor 球/偏应变能分解方法,也可建立球/偏应变能分解的复合型相场模型:
比较可知,上述2个复合型相场模型的本质区别在于HI和HII的物理意义不同:基于拉/压应变能分解的复合型相场模型认为只有受拉部分的应变能驱动I 型和II 型裂纹扩展,实际上受压部分的应变能也会影响II 型裂纹扩展;而基于球/偏应变能分解的复合型相场模型则认为受拉部分的球应变能驱动I 型裂纹扩展、偏应变能驱动II 型裂纹扩展。因此,两者的HI公式表达式类似,但HII差别很大。
1.3 复合型相场模型的交错法求解
采用交错算法[22],借助ABAQUS 有限元软件平台,自行编写材料本构模型的用户子程序UMAT 和驱动相场变量演化的用户子程序HETVAL,可实现复合型相场模型的数值求解。首先,通过对控制方程(式(2),(9)或(10))进行线性离散,得到其数值弱形式:
式中:Bu,Bφ和Nu,Nφ为位移场和相场的空间导数矩阵和形状函数矩阵,∂σ∕∂ε为雅可比矩阵。
其次,采用交错法分步求解公式(11)~(13)中的变量u和φ,即将平衡方程和相场演化方程当作2个独立的方程分别进行求解。最后依托ABAQUS软件平台完成求解过程:首先在主程序中构建几何模型并设置材料参数和边界条件,其中:u0=0为初始位移,Δu为每个加载步的恒定位移增量(为保证计算精度,Δu尽可能取小),uf为预设的加载总位移(为保证材料破坏,uf尽可能取大),并计算应变张量ε;其次,将ε传递到子程序UMAT 中,在该子程序中通过定义本构方程∂σ∕∂ε(公式(13))并利用ε求解平衡方程(式(11))得到应力张量σ,并通过式(9)和(10)计算历史场变量HI和HII;最后,将HI和HII传递到子程序HETVAL 中通过相场演化方程(式(12))计算出相场变量φ。如此循环,直到un=uf结束。
2 多裂纹扩展模拟计算
本文以单轴压缩下含双平行裂纹的红砂岩试件作为算例,采用基于拉/压应变能分解和球/偏应变能分解的2种复合型相场模型,分别模拟计算红砂岩试件从裂纹起裂、扩展到贯通破坏全过程,并与试验结果进行对比分析。
2.1 计算模型
如图2 所示,红砂岩试件尺寸为150 mm×150 mm×40 mm,内含2 条与水平方向夹角为β=45°的平行裂纹AB 和CD,长度均为2a=30 mm,垂直间距为h=20 mm。2 条裂纹中心点连线沿裂纹方向的投影距离(简称中心点平行间距)分别为s=15 ,30 ,45 和60 mm。表1 列出了红砂岩的基本力学性能参数,其中:弹性模型E和泊松比v由单轴压缩试验测得,I型断裂韧度KIC由三点弯试验测得,II 型断裂韧度KIIC由剪切盒试验测得,I 型、II型临界能量释放率(GIC、GIIC)根据I 型、II型断裂韧度(KIC和IC)和弹性模量E计算得到(GC=K2C/E),并设定相场数值参数为l=0.2 mm。采用下端固定的位移边界条件、上端恒定位移的加载边界形式,位移增量Δu=0.02 mm,最大位移uf=4.5 mm。选取平面应力单元(CPS4)进行网格划分,并在2 条裂纹尖端附近细化网格(单元最小尺寸为0.1 mm)。

图2 双平行裂纹试件计算模型Fig. 2 Calculation model of the double-cracked specimen

表1 红砂岩基本力学性能参数Table 1 Basic mechanical properties of the red sandstone
2.2 计算结果与分析
为了描述简便,以下将基于拉/压应变能分解的复合型相场模型简称为T/C-PFM(PFM 相场模型英文缩写),将基于球/偏应变能分解的复合型相场模型简称为V/D-PFM。
2.2.1 基于拉/压应变能分解的复合型相场模型
图3~6 为T/C-PFM 计算得到的单轴压缩下含双平行裂纹的红砂岩试件裂纹扩展演变过程,其中黑色代表新萌生的裂纹(相场变量φ=1),白色代表试件完好部分(相场变量φ=0)。
可见,当s较小时(s=15 mm),4 个裂纹尖端同时出现翼裂纹(I 型)起裂并沿垂直于原裂纹面方向扩展(图3(a),3(b));随着荷载增加,裂纹尖端B和C处萌生了共面次生裂纹(II 型)并扩展至边缘导致试件破坏(图3(c)和3(d)),其中岩桥贯通模式为B和C尖端的翼裂纹分别扩展至D和A尖端(图3(c))。

图3 不同位移加载步下双裂纹扩展数值模拟结果(s=15 mm)Fig. 3 Simulation results of the double-crack propagation under different loading steps (s=15 mm)
当s持续增大(s=30 mm,45 mm,60 mm),首先仍在4个尖端处出现沿垂直于原裂纹面方向的翼裂纹(I 型)起裂扩展(图4(a)~6(a)),而后发生不同形式的岩桥贯通模式:当s=30 mm 时,由B和C尖端处的翼裂纹分别扩展至C和B尖端形成贯通(图4(b));s=45 mm 和s=60 mm 时贯通模型相同,即由B和C尖端处2 条翼裂纹间出现新裂纹相向扩展至贯通(图5(b)和6(b))。随着加载继续增加,在A和D尖端处出现共面次生裂纹(II 型)扩展至试件边缘导致试件破坏(图4(c)-4(d)-6(c)-6(d))。可见,随s不断增大,当2 条平行裂纹之间的相互影响逐渐变小,裂纹外尖端(A和D)的起裂破坏形式(图4~6)趋近单裂纹单轴压缩试验结果[23-25]。

图4 不同位移加载步下双裂纹扩展数值模拟结果(s=30 mm)Fig. 4 Simulation results of the double-crack propagation under different loading steps (s=30 mm)

图5 不同位移加载步下双裂纹扩展数值模拟结果(s=45 mm)Fig. 5 Simulation results of the double-crack propagation under different loading steps (s=45 mm)
2.2.2 基于球/偏应变能分解的复合型相场模型
图7~10 为V/D-PFM 计算得到的单轴压缩下含双平行裂纹的红砂岩试件裂纹扩展过程,其中黑色代表新萌生的裂纹(相场变量φ=1),白色代表试件完好部分(相场变量φ=0)。该模型模拟结果中裂纹起裂点、起裂扩展方向、二次裂纹种类和岩桥贯通破坏模式均不同于T/C-PFM 模拟结果。当s较小时(s=15 mm),裂纹起裂点并非同时发生在2条裂纹的4个裂纹尖端(图3(a)),而仅发生在2个裂纹尖端A和D处,且起裂扩展方向并非沿垂直于原裂纹面方向而是沿近似竖直方向(图7(a)),但两者均为翼裂纹(I 型)起裂。随着荷载增加,在A和D处的翼裂纹扩展方向逐渐转向平行于原裂纹面方向,并在裂纹尖端B和C处出现了反翼裂纹(II 型)扩展(图7(b))而并非共面次生裂纹(图3(c));接着在A和D处的翼裂纹继续扩展至试件边缘,并且在A和D处出现反翼裂纹扩展(图7(c));最后的岩桥贯通是A和D处的反翼裂纹分别扩展至另一条裂纹尖端C和B处形成裂纹贯通而导致试件破坏(图7(d))而非翼裂纹(图3(d))。
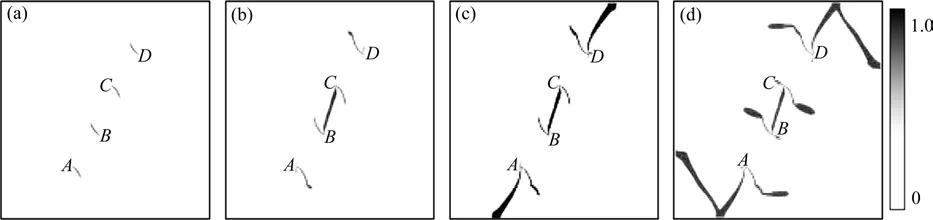
图6 不同位移加载步下双裂纹扩展数值模拟结果(s=60 mm)Fig. 6 Simulation results of the double-crack propagation under different loading steps (s=60 mm)

图7 不同位移加载步下双裂纹扩展数值模拟结果(s=15 mm)Fig. 7 Simulation results of the double-crack propagation under different loading steps (s=15 mm)

图8 不同位移加载步下双裂纹扩展数值模拟结果(s=30 mm)Fig. 8 Simulation results of the double-crack propagation under different loading steps (s=30 mm)

图9 不同位移加载步下双裂纹扩展数值模拟结果(s=45 mm)Fig. 9 Simulation results of the double-crack propagation under different loading steps (s=45 mm)
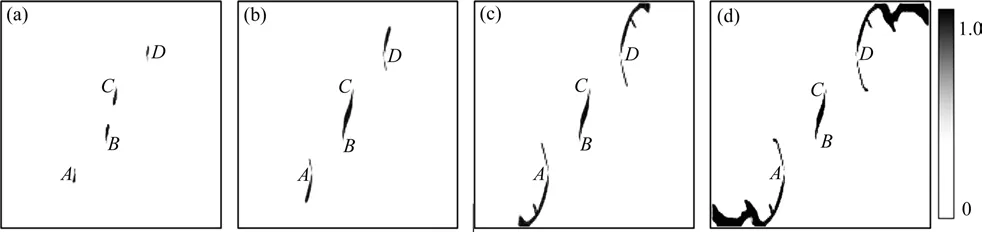
图10 不同位移加载步下双裂纹扩展数值模拟结果(s=60 mm)Fig. 10 Simulation results of the double-crack propagation under different loading steps (s=60 mm)
当s=30 mm 时,在4个裂纹尖端处出现翼裂纹(I 型)起裂并沿近似竖直方向扩展,但A和D尖端处裂纹扩展更快(图8(a)和8(b));而后B和C处的翼裂纹逐渐扩展至另一条裂纹中间位置形成贯通,A和D处的翼裂纹扩展方向逐渐变为平行于原裂纹面方向(图8(c));最后A和D尖端处翼裂纹扩展至边缘导致试件破坏(图8(d))。随着s继续增大(s=45 mm 和60 mm),裂纹起裂扩展至破坏的形式趋于稳定(图9~0):在4 个裂纹尖端出现翼裂纹(I型)起裂并沿近似竖直方向扩展(图9(a)和10(a));接着尖端B和C处的翼裂纹相向扩展至贯通(图9(b)和10(b));当荷载继续增加,在A和D处出现反翼裂纹(II型)扩展(图9(c)和10(c)),最后A和D尖端处翼裂纹扩展方向逐渐转向平行与原裂纹面的方向直至扩展到边缘导致试件破坏(图9(d)、10(d))。由图4~6 和图8~10 可以得出,随着中心间距s的增大,2 种模型模拟结果的差异性(包括起裂扩展方向、二次裂纹种类和破坏模式)没有明显变化(同s=15 mm时情况)。
2.2.3 2种复合型相场模型模拟结果比较
关于裂纹起裂的比较:T/C-PFM 和V/D-PFM的模拟结果中均为翼裂纹(I 型)起裂,但起裂点与起裂扩展方向不同。前者两条裂纹在不同的s情形下均为4个尖端同时沿着垂直于原裂纹面的方向起裂,后者并非同时起裂,当s较小时最先由2 个外尖端(A和D)出现翼裂纹起裂,当s较大时,2 个内尖端(B和C)距离变近、相互影响变大,导致内尖端(B和C)处起裂扩展更快(起裂扩展方向沿近似竖直方向)。
关于二次裂纹的比较:T/C-PFM 和V/D-PFM的模拟结果中次生裂纹虽然都为II型裂纹,但前者模拟出现的为共面二次裂纹,而后者模拟中出现的为反翼裂纹,这是因为2 种复合型相场模型的II型裂纹驱动力HII(式(16)和(17))的差别很大,前者认为受压部分应变能不驱动II型裂纹扩展。
关于岩桥贯通与破坏模式的比较:当s较小时,T/C-PFM 和V/D-PFM 的模拟结果中虽然岩桥贯通的轨迹相同(均为尖端B和C分别于尖端D和A间形成贯通),但前者为I 型裂纹贯通(图3(d)),而后者为II 型裂纹贯通(图7(d))。当s不断增大,2 种相场模型模拟的岩桥贯通与试件的最终破坏形式都趋于稳定:模拟结果均为2个内尖端(B和C)产生裂纹相互贯通,但前者模拟结果的贯通裂纹是加载一段时间后在2个内尖端(B和C)处新萌生的倾斜次生裂纹(图6(b)),而后者模拟结果中的贯通裂纹为内尖端(B和C)最先出现的翼裂纹相向扩展形成(图10(b))。分析最后的破坏形式,前者模拟为共面次生裂纹扩展至试件边缘导致最终破坏,而后者模拟则为翼裂纹扩展至边缘导致最终破坏。
可见,双平行裂纹的中心间距对裂纹的起裂点位置和起裂方向影响较小,均在4个裂纹尖端发生I 型起裂(形成4 条翼裂纹),但对翼裂纹扩展导致的岩桥贯通模式和二次萌生裂纹(发生在原裂纹尖端)较大。当中心间距较小时,2条裂纹之间2组较近的尖端(A,C和B,D)干涉作用较大,形成了2 个应力场增强区而导致了2 组贯通裂纹,原裂纹外尖端因应力得到释放而避免了二次裂纹萌生;当中心间距较大时,2 条裂纹之间仅较近的内尖端(B和C)裂尖干涉作用较大,只产生了一个应力场增强区和内尖端之间的一组贯通裂纹,2 个外尖端仅发生翼裂纹扩展对原裂尖的应力场影响较小,故较易出现二次萌生裂纹。中心间距对最后的破坏轨迹基本上无影响,均为2个裂纹外尖端的翼裂纹扩展导致试件破坏。
总之,上述2 种复合型相场模型均可模拟出I型和II 型裂纹扩展,但2 种模型驱动II 型裂纹扩展的II 型历史场变量HII差别较大(见式(9)和(10)),从而导致模拟的II型裂纹形式明显不同:T/C-PFM模拟出共面次生裂纹(扩展方向平行原裂纹面),V/DPFM 模拟出反翼裂纹(扩展方向与翼裂纹方向相反),2 种模型在模拟断裂问题的有效性和适用范围需要进一步试验验证。
3 试验验证
3.1 试验方案
采用与2.1 计算模型相同的双平行裂纹试件进行单轴压缩试验进行验证。岩石材料选取产自云南楚雄市武定县的红砂岩,其基本力学参数同表1。试件尺寸为150 mm×150 mm×40 mm,采用水刀切割机预置不同中心水平间距s的双平行裂纹(裂纹长30 mm,裂纹与水平方向夹角45°,s=15,30,45 和60 mm)。试验设备为SANS 微机控制伺服刚性试验机(图11),采用力控加载方式,加载速率为50 N/s,通过数码相机拍摄记录试件的最终破坏形式。

图11 SANS微机控制伺服刚性试验机Fig. 11 Computer control electro-hydraulic servo universal testing machine
3.2 试验结果与分析
图12 为单轴压缩下含双平行裂纹的红砂岩试件断裂轨迹。当s=15 mm时(图12(a)),双平行裂纹间相互作用影响明显,只在A尖端处出现翼裂纹(I型)扩展,并且起裂扩展方向受裂纹间相互作用影响近似为竖直方向,D处因为岩石不均匀性未出现对称翼裂纹。并且在4个裂纹尖端均出现了与反翼裂纹(II 型)扩展,最后A和D尖端处的反翼裂纹分别扩展至C和B尖端处形成岩桥贯通。当s增大时断裂轨迹发生改变(s=30 mm,图12(b)),首先在B,C和D尖端处均萌生翼裂纹起裂并沿近似垂直于原裂纹面方向扩展,其次在4个尖端处都出现了反翼裂纹扩展,值得注意的是A尖端除了出现了反翼裂纹还出现了共面次生裂纹,这说明2 种II型裂纹都是合理的,但该试验中反翼裂纹更易萌生。岩桥贯通模型变为内侧尖端(B和C)的翼裂纹扩展至另一条裂纹形成贯通破坏。随着s的继续增大(图12(c)和12(d))裂纹间相互作用影响变小,试验的断裂轨迹变得相似:4 个尖端均会出现翼裂纹起裂并沿近似垂直于裂纹面方向扩展,在裂纹外尖端(A和D)会出现反翼裂纹和共面次生裂纹(图12(c))。裂纹间岩桥贯通模式为B和C尖端的翼裂纹相向扩展至贯通形成破坏。

图12 红砂岩试件断裂轨迹试验结果(不同的中心平行间距s)Fig. 12 Fracture trajectories of the double-cracked sandstone specimen (with different s)
3.3 试验结果与模拟结果对比分析
对比分析试验与模拟结果,当s较小时,2 种相场模型都能模拟出试验中2 个外尖端的翼裂纹(I型)扩展,但相比于前者,后者成功地模拟出4 个尖端的反翼裂纹,并且岩桥贯通模式也与试验相同均为反翼裂纹贯通。当s=30 mm 时,T/C-PFM和V/D-PFM 2种模型成功模拟出4个裂纹尖端处的翼裂纹扩展;并且2种相场模型模拟的岩桥贯通模式与试验吻合均为内尖端的翼裂纹(I 型裂纹)相互扩展至另一条裂纹处形成贯通。随着s的继续增大(s=45 mm 和60 mm),后者模拟的结果与试验结果更为贴合,可以准确地模拟出2 个外尖端的翼裂纹、反翼裂纹的扩展和2 个内尖端之间的翼裂纹贯通。
综上所述,2 种复合型相场模型均能较好地模拟单轴压缩下含双裂隙岩石试件的I 型、II 型裂纹扩展,但V/D-PFM 模型比T/C-PFM 模型能更准确地模拟出双裂纹外尖端(A和D)的II 型裂纹扩展轨迹(反翼裂纹)和双裂纹内尖端(B和C)的岩桥贯通轨迹(翼裂纹直接扩展贯通)。这是因为T/C-PFM 模型仅考虑了拉应变能对II型裂纹扩展的影响,而实际上压应变能也将影响II 型裂纹扩展;V/D-PFM 模型因同时考虑拉、压应变能对II型裂纹扩展的影响而更具有优越性。
4 结论
1) 基于能量断裂F-准则,给出了基于球/偏应变能分解的复合型相场模型;通过自行设计ABAQUS 软件的本构子程序UMAT 和驱动相场变量演化子程序HETVAL,建立了基于拉/压和球/偏应变能分解2 种复合型相场模型的交错求解方法,实现了复杂环境下多裂纹扩展模拟。
2) 2 种复合型相场模型模拟的双平行裂纹具有相同的起裂机理(I 型)和扩展机理(II 型)、不同的起裂点位置和方向(T/C-PFM 模型为4 个裂纹尖端同时沿垂直于原裂纹面方向起裂扩展、V/D-PFM 模型为2 个裂纹外尖端沿竖直方向起裂扩展)、二次萌生裂纹扩展轨迹(T/C-PFM 模拟为共面次生裂纹、V/D-PFM 模型为反翼裂纹)和岩桥贯通轨迹(T/CPFM模型为2个内尖端的翼裂纹之间出现新裂纹扩展贯通、V/D-PFM 模型为2 条翼裂纹相向扩展贯通。
3) 采用2种复合型相场模型模拟分析了平行裂纹的中心间距对裂纹扩展全过程的影响规律,即中心间距对裂纹起裂点位置和起裂方向(I 型翼裂纹)影响较小,但影响岩桥贯通轨迹(如间距较小时,相邻的2 组裂纹尖端相向扩展为2 条贯通裂纹;间距较大时,相邻的一组内裂纹尖端相向扩展为一条贯通裂纹)和二次萌生裂纹(如间距较小时出现在2 个内尖端、间距较大时出现在2 个外尖端)。最后的破坏轨迹基本上不受中心间距的影响,均为2个裂纹外尖端的翼裂纹扩展导致试件破坏。
4) 通过开展不同中心水平间距s下含双平行裂纹的红砂岩试件单轴压缩试验,验证了2种复合型相场理论模型均能有效地模拟岩石多裂纹I 型、II型裂纹扩展,但基于球/偏应变能分解的复合型相场模型模拟的反翼裂纹(II 型)扩展轨迹和岩桥贯通轨迹(2 条翼裂纹相向扩展贯通)与试验结果更为吻合,更适合于复杂加载条件下多裂纹扩展行为模拟。

