“四新”建设背景下基于问题驱动的大学数学教学模式探索——以高等数学教学为例

于莉琦，贺树立，吴方亮

（1.黑龙江东方学院 黑龙江 哈尔滨 150066 2.哈尔滨市第十四中学 黑龙江 哈尔滨 150000）

1 高等数学教学现状

大学数学学习是数学核心素养培育的关键期。高等数学课是众多专业培养计划中必须开设的基础课程，为学生后续专业学习提供必要的理论支撑。但目前高等数学教学存在着亟待解决的痛点问题。首先，作为重要的专业基础课，高等数学的教学中普遍存在重理论推演少实践应用的现象，教师在教学中对知识的应用性讲授不足。其次，传统数学课程的教学模式单一，学生的课堂参与度不高，课堂教学主要以教师讲授为主，师生互动不充分。随着信息技术的迅猛发展，当下智慧课堂越来越受到人们的关注和认可，如何构建高效的信息化课堂教学模式，解决数学教学中的痛点问题是当下一线教师面临的主要挑战。

课程是人才培养的核心要素，教学改革改到深处是课程。在“四新”建设理念的引领下，近年来，大学数学教学创新研究不断深入。黄华等系统研究了大学数学“金课”建设的路径，通过分析大学数学“金课”建设面临的困难和挑战，立足地方高校，进行了创新制度、创新课程、课程思政、学科竞赛和师资队伍建设五个方面的探索实践。曾祥艳等以大学生创新实践能力的培养为目标，通过创新教学思维，开设数学软件实验课、将教师科研方向与教学相结合等方式来激发学生的自主创新精神。史永堂、俞能福等在大学数学教学中充分发掘思政元素，不断探索课程思政的新途径，提升课程教学的温度，将育人育才相结合。

依托黑龙江省教育科学规划课题的开展，课题组针对教学中的痛点，从教学内容设计、教学活动设计、教学评价与考核三个重要环节进行了改革实践，构建了以“三引导一融入”为教学创新点，以线上线下混合式教学为依托，以全过程评价为衡量标准的教学模式，旨在提升学生的数学核心素养，促进学生全面发展。

2 采用“三引导一融入”方式创新教学内容设计

高等数学的主体内容是微积分，微积分知识体系的产生源于人们在生产实践中对实际问题的研究，并在实际应用中不断深化和完善。在高等数学课程的教学中，通过设计情境问题，引导学生一步步地探索求知，有意识地培养学生的数学思维，提高学生应用数学知识思考问题、解决问题的能力。在教学内容的设计中，课题组采用了“三引导一融入”的方式。

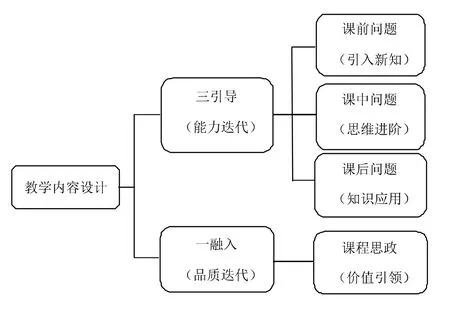
图1 三引导一融入

三个引导问题的设计目的在于重现知识发生、发展的过程，有意识地培养学生的数学思维和应用数学的意识。课前问题的设计要适应本节课的教学主题，同时具有可操作性，问题最好是开放性的，让学生们以小组讨论的形式完成，如此进行新知引入有利于培养学生的抽象思维能力和建模能力。课中问题的设计要突出本节课教学的重点和难点，教学过程中要注意启发学生进行逻辑推理，并提升学生的数学计算能力。课后问题的设计要突出知识的应用性，课后问题需要具有一定的创新性和挑战度，目的是让学生加深对所学知识的理解，提升数学应用的能力。下面以可分离变量微分方程的教学为例进行教学内容的设计。

课前问题：新中国成立以后，先后于1953年、1964年和1982年进行了3 次人口普查。1990年进行了第四次人口普查，自1990年后每10年进行一次人口普查，目前已进行人口普查七次（普查数据包括人口总数和人口增长率），请根据前六次的人口普查数据预测第七次普查的人口数，并验证你的结果，分析误差原因。

课中问题：如何利用不定积分的知识，求可分离变量微分方程：dy=f x g y dx的通解。

课后问题：①已知物体的温度为100℃，将其放置在空气为20℃的环境中冷却，试求物体温度随时间的变化规律。(已知物体温度的变化率与物体温度和当时空气温度之差成正比)。②放射性元素铀由于不断地有原子放射出微粒子而变成其他元素，铀的含量就不断地减少，这种现象称为衰变。由原子物理学知道，铀的衰变速度与当时未衰变的原子的含量I成正比，已知t=0时，铀的含量为I0，求在衰变过程中铀的含量I t随时间t变化的规律。③一地区发生某传染病，该地区人口数目800 人，12 小时后有3 人发病，由于这种传染病没有早期症状，故传染者不能被及时隔离，已知60 小时后有被感染检测设备运到，试估计设备到达时已有多少人被感染。

一融入：长期以来，人类与传染性疾病进行了不屈不挠的斗争。传染病动力学是对传染病进行理论性定量研究的重要方法，它是根据疾病发生和传播的规律，建立能够反映传染病动力学特性的数学模型，通过对模型的研究揭示疾病流行的规律，预测其发展的趋势。在数学建模的过程中，微分方程起到了十分重要的作用。1911年公共卫生医生ROSS 博士利用微分方程模型对疟疾在蚊子与人群之间传播的动态行为进行了研究，其结果表明如果将蚊子数量控制到一个临界值以下，疟疾的流行就可以得到有效的控制，他的这项研究获得了Nobel 医学奖。通过建模分析研究传染病的动力学性质，能够为疾病防控提供理论支撑，为守护人类健康做出贡献。

以问题为导向构建教学内容，可以很好地让学生体会数学思想、数学文化和数学精神，有利于激发学生的学习兴趣，增强学生应用数学知识研究问题、解决问题的能力。在教学过程中注重课程思政，将知识传授与价值引领有机结合，让高校课堂更好地肩负起育人育才的责任。

在“三引导一融入”课程内容构建理念下，教学团队通过不断挖掘，建立了知识应用案例库和课程思政案例库，收集案例的过程中，教师的知识应用水平和课程思政能力也得到了很大的提升。

3 借助教学软件，开展线上线下联动式教学活动

教学创新改革得以实现的重要原因是信息技术的发展进步，尤其是近几年教学辅助软件不断升级，线上教学资源越来越丰富。在此条件下，开展线上线下联动的教学活动，不仅能够丰富教学内容，提高教学效率，更重要的是加强了师生之间的交流，学生有更多的机会向老师请教，教师也能够更准确地了解学生的学习情况和学习需求，有利于因材施教，真正做到以学生为中心。

线上线下混合教学可分为课前、课中、课后三个阶段。以可分离变量微分方程教学为例，课前，教师创建自学任务：①自学微分方程基本概念并完成相应测试题；②发布课前问题，分组讨论人口预测的方法，每组推选代表进行课上阐述。课中，教师总结课前自学和测试完成情况，重点讲授可分离变量微分方程通解的计算方法，并进行课堂练习、测试以及绘制本节知识的思维导图。期间引入课程思政。课后，教师布置两项任务：①基本计算练习；②知识应用题。同学完成作业后回传到指定平台，教师可以随时批阅，了解学生的作业情况，教师可以根据教学需要随时上传学习资源，辅助学生课后学习。

同时注意到，大学数学中一些基本概念和基本计算方法已经在高中教学中有所体现，比如极限、连续、导数、积分等概念。高中阶段学生对这部分知识掌握情况不尽相同，但这些内容对于后续学习又十分重要，教师仍需抓重点讲详细。由于学生对于上述知识已经初步学习，虽然掌握的程度基本达不到大学数学的学习要求，但重新讲授可能会导致一些学生失去学习兴趣，故教师要特别注意，建议采用问题驱动教学方法，将基本概念以资源形式进行线上分享，线下活动设计更具有高阶性和挑战度的问题来激发学生的学习兴趣，效果更佳。

在线上线下混合教学模式下，教学内容、教学设计与教学模式要相辅相成，相互促进，才能更好地发挥混合式教学的优势，提升教学效果。

4 改革考核方式、施行全过程评价

数学课程的考试方式多以试卷考试为主，但近年来，随着教学改革的不断深入，在考核考试方面有了很大的改变，教师加强了学生日常学习过程中的考查，更加注重学生学习过程中的效果和学习的常态化检测。

目前，我们对学生的考核采取“五五分”的考核标准，总评成绩100 分，其中学生过程性评价占50 分，期末试卷成绩占50 分。过程性评价标准与教师的教学内容设计与教学活动相对应，分为课前评价、课中评价和课后评价三部分，如表1 所示。

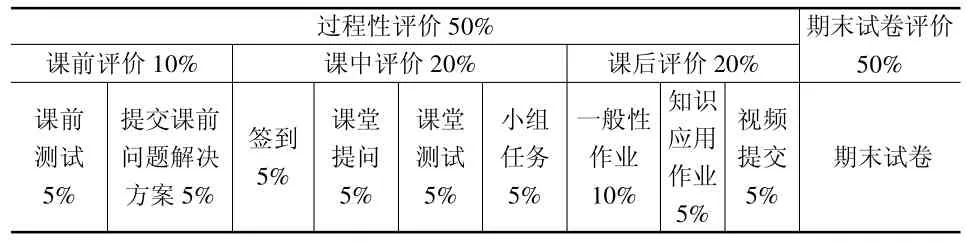
表1 综合评价构成

在过程性评价中，学生日常学习的任务更加具体，学习效果能够得到量化，这样不仅能督促学生养成好的学习习惯，同时也能激发学生学习的动力。

5 参加竞赛，提升能力

数学类学科竞赛主要包括全国大学生数学竞赛和数学建模竞赛。近几年来，课题组教师在学生入学的第一节数学课上都特别开设课程导论，除了介绍课程发展史、课程特点外，还必须介绍数学各类竞赛的情况，并积极宣传学校学生已取得的优异成绩，目的是激发学生参与竞赛的激情和欲望。对于各类竞赛，课题组教师都会积极组织并参与，通过几年的努力，学校师生参与各项竞赛活动的人数逐年上升，竞赛成绩也逐年提高。

6 结论

大学数学教学创新研究是适应新时代、新要求，推进高校教育改革的必然选择。在“四新”建设背景下，针对教学过程中存在的痛点问题，教学团队从教学理念、教学方式方法、考核方式三个方面进行改革实践，努力实现知识传授与价值引领的有机结合，构建了“三引导一融入”的教学设计方法，依托线上线下相结合的方式提升了教学效率，通过对学生的全过程评价激发了学生学习的积极性。通过不断地探索实践，高等数学课程的教学效果有了显著的提升，为学生全面发展打下坚实的基础。