基于长期健康监测数据的混凝土单箱三室箱梁遮阴效应

寇越，刘金义，马彦阳，张峰

(1.中国铁建投资集团有限公司，北京 100855； 2.山东大学岩土与结构工程研究中心，济南 250061)

桥梁结构在服役期长期暴露于露天环境中，在太阳辐射、日温变化、年温变化、寒流等多因素的影响下，结构内部逐渐形成不均匀温度分布，对桥梁结构的内力影响显著，由此产生的温度应力与变形在桥梁设计荷载中占有很大比重[1-2]。在太阳辐射条件极端的时间和地区，日照温度作用的影响甚至超过恒载和活载成为第一控制作用，对桥梁的耐久性与安全运营造成较大的危害。

结构温度场研究的主要通过少量测点结合数值模拟实现。叶见曙等[3]通过对南京长江二桥的现场实测分析，得出双幅分离的箱梁桥结构竖向温度梯度分布规律。郭棋武等[4]、颜东煌等[5]、王伟[6]、Xu等[7]也通过简单的数值模拟与实测数据对比的方法，证明了箱梁内部的温度场是非线性的。徐丰[8]借助ANSYS内嵌的辐射矩阵生成器，实现了混凝土箱梁外表面在任意时刻日影单元与非日影单元的区分。尹冠生等[9]利用光线追踪法编制了ANSYS子程序，准确模拟了混凝土拱桥拱上主梁的遮阴作用。Zhu等[10]建立了混凝土斜拉桥的三维温度场遮阴精确模型。对于单箱三室梁而言，多个箱室的存在导致对流边界条件极其复杂，解决这一问题需要在单箱三室箱梁截面埋置大量测点。仅凭借少数测点和数值模拟结合的手段难以有效准确地反映单箱三室箱梁的温度场实际情况，这也是目前很多研究所遇到的瓶颈。

相比有限元数值模拟，通过对实桥或模型的长期测试可以反映桥梁结构真实的温度分布状态。Maes等[11]依托加拿大阿尔伯塔省轻轨大桥提出加拿大温度规范的修正方法。Shushkewich等[12]基于全年的实测数据证实了AASHTO规范中正负温度梯度的规定。Peiretti等[13]基于桥面板的长期测量试验，认为每日温差大于10 ℃的地方需要重新考虑最大温度梯度。Hedegaard等[14]发现使用AASHTO的规范进行有限元软件建模的结果显著低于测量结果。上述这些研究还是基于传统的研究方法，验证或者改进了规范中的取值。Barsotti等[15]运用数理统计计算98%上限值对应的温度梯度。顾瑞海等[16]基于实测数据分别计算了重现期为50年和100年的箱梁竖向温差代表值。王毅[17]用假设检验和参数分析提出计算混凝土箱梁温度作用代表值的方法。雷笑[18]采用系统聚类分析与非参数统计方法对混凝土箱梁日最大竖向温差进行研究，相应分别得到了最大正温差和最大反温差所对应的标准值、频遇值和准永久值。陶翀等[19]对箱梁的竖向最大正温差与环境气温之间的关系进行统计分析，并建立了基于极值统计理论的正温度梯度曲线。然而这些研究基于单箱单室或者预制混凝土梁，对于复杂的单箱三室梁是否适用仍然存在疑问。

目前针对单箱三室箱梁的温度场研究较少。程曙光等[20]以西安西咸新区红光路沣河大桥为研究对象,在混凝土表面布置了58个温度传感器，并在南北两支座处布置了2个位移传感器，结果表明根据形心点温度进行支座位移计算时误差较小。然而该研究仅仅考虑了箱梁整体的位移，并未考虑箱梁细部的开裂问题。潘旦光等[21]以西安西咸新区沣河大桥的单箱三室预应力混凝土箱梁为研究对象，在混凝土外表面粘贴了65个温度传感器研究混凝土温度场分布规律。然而混凝土是一种离散性较大的非金属材料，仅在混凝土表面粘贴传感器不能反映实际桥梁的温度规律，因此在单箱三室梁截面内部埋置大量的温度场传感器十分必要，现通过在王家河特大桥埋置大量温度测点进行测试，研究适用于单箱三室箱梁的温度场分布规律，以期对其他同类型桥梁提供参考。

1 箱梁温度试验

王家河特大桥全长2 014.829 m(图1)，主桥为五塔六跨预应力混凝土矮塔斜拉桥，采用塔、墩、梁固结刚构体系，主跨为230 m。为研究该桥单箱三室箱梁温度分布规律，选择王家河特大桥12号主墩大里程方向26#断面开展温度测试。

图1 王家河特大桥Fig.1 Wangjiahe grant bridge

26#横断面梁高为3.8 m，桥面板宽度为29.5 m，底板宽度为18.6 m (图2)，测试截面共布置89个温度传感器(图3)。

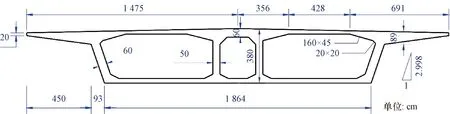
图2 测试截面尺寸图Fig.2 Dimensional diagram of the test section

图3 测点布置图 Fig.3 Measurement point layout

测试截面的温度传感器采用的是预埋式JMT-36C智能温度传感器，太阳辐射传感器采用的是JMGD-1G传感器，采用无线远程自动化采集模块进行温度和太阳辐射测试，采集频率为1次/h，现场测试布置测试如图4所示。

图4 现场测试图Fig.4 Field test diagram

采集模块由JMTX-2020型DTU手机上网模块连接，以实现远程数据采集。采集模块和DTU上网模块安装于全密封标配机箱内，以保证采集设备的稳定性，测试设备如图5所示。

图5 测试设备示意图Fig.5 Schematic diagram of the test equipment

2 环境因素分析

基于已有箱梁温度效应的研究表明[22-23]，影响箱梁温度梯度的主要因素为大气温度、风速和太阳辐射，因此介绍测试期间大气温度传感器、风速传感器、太阳辐射传感器的测试值。选取大气温度进行分析，测试期间为2020年10月6日—2021年10月6日，测试期间太阳辐射和温度情况如图6所示。

图6 测试期间气象参数统计Fig.6 Statistics of meteorological parameters during the test

测试期间2021年4月20日—5月18日太阳辐射传感器和风速传感器出现故障。由图6(a)可以看出，日最大太阳辐射值随季节变化明显，夏季太阳辐射值高于冬季。日最大太阳辐射值出现在2021年6月5日，为1 024.89 W/m2，冬季(12—次年2月)最大太阳辐射值为664.02 W/m2。由图6(b)可以看出，日平均风速范围在1.0～3.0 m/s，试验期间记录的最大风速约为5.94 m/s，而日最小风速为0.11 m/s，无明显季节分布规律。测试期间大气温度分布状态见图7。

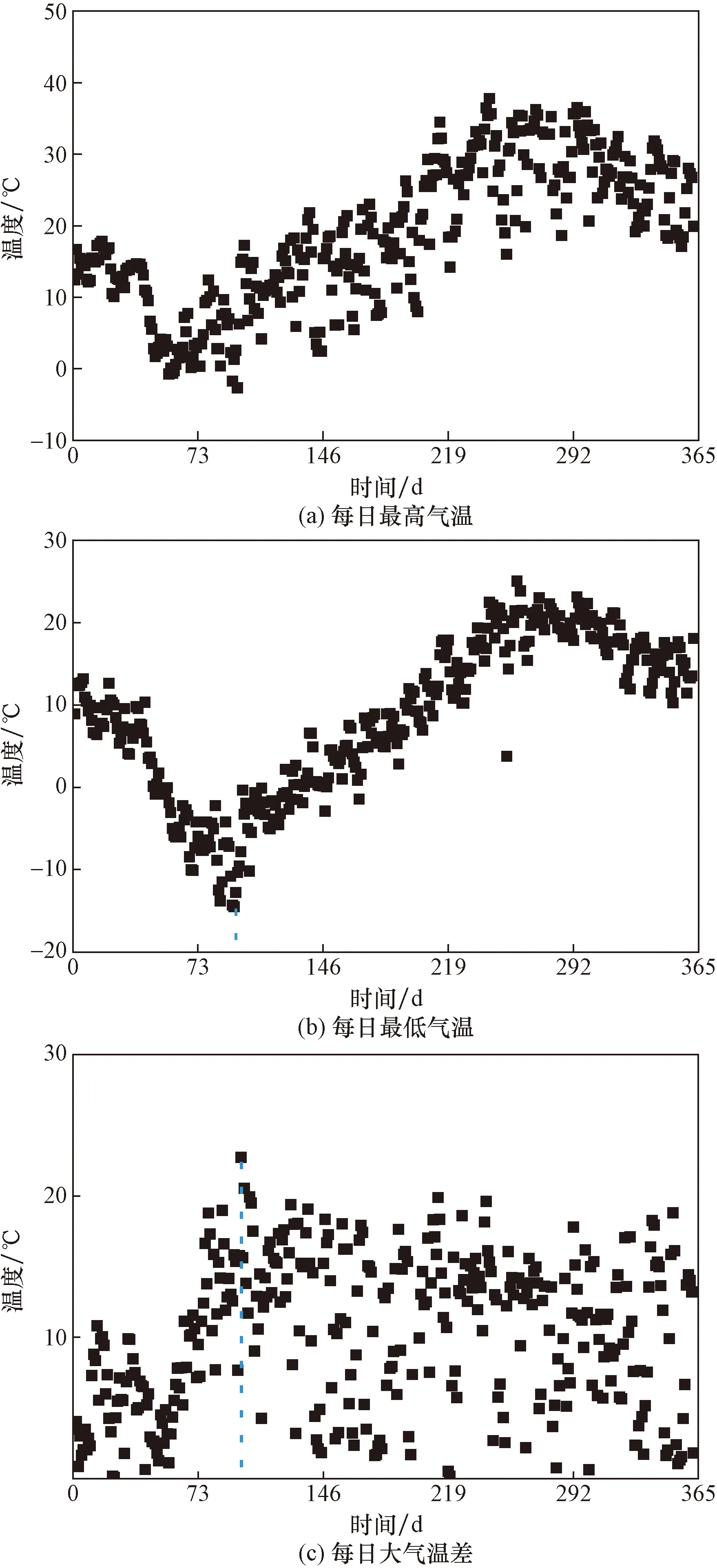
图7 测试期间每日大气温度记录Fig.7 Daily atmospheric temperature records during the test period

由图7可知，采集的大气温度最高气温出现在8月1日，气温为36.5 ℃；最低气温出现在1月8日，气温为-14.5 ℃。统计梁体平均温度和大气温度的关系(图8)，提出箱梁平均温度预测公式分别为

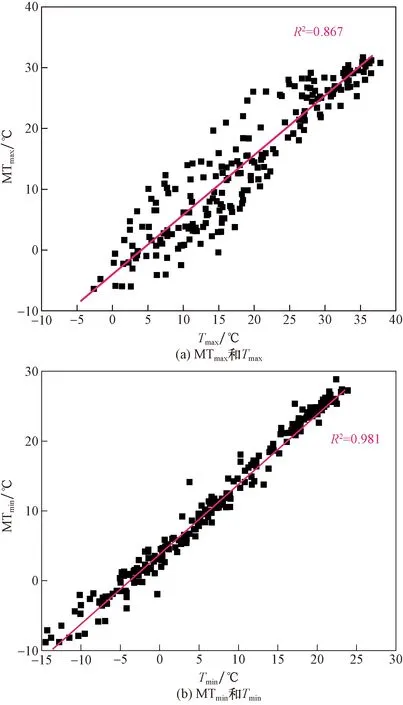
图8 桥梁每日平均温度Fig.8 Average daily temperature of the bridge

MTmax=0.97Tmax-4.094 7

(1)

MTmin=1.01Tmin+4.078 4

(2)

式中：MTmax为梁体最高平均温度，℃；MTmin为梁体最低平均温度，℃；Tmax为大气最高温度，℃；Tmin为大气最低温度，℃。

由图8看出，箱梁梁体平均温度和大气温度密切相关，MTmax和Tmax之间的决定系数R2值为0.867，MTmin和Tmin之间的决定系数R2值为0.981，因此可通过式(1)和式(2)预测箱梁截面每日平均温度的最大值和最小值。

为表征不同季节箱梁平均温度与环境温度的相关性，分别绘制温度场模型秋季(2020年10月9日)、冬季(2020年1月14日)、春季(2021年4月10日)以及夏季(2021年8月5日)平均温度与大气温度对比曲线，如图9所示。

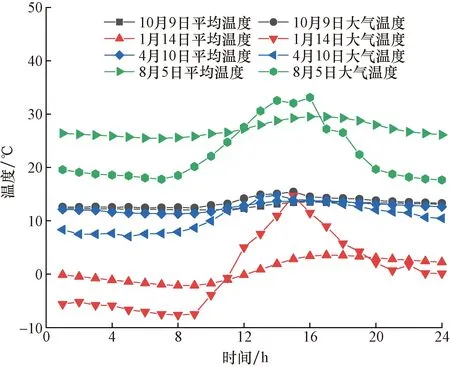
图9 梁体平均温度和大气温度对比Fig.9 Comparison of average beam temperature and atmospheric temperature

分析图9可以看出，箱梁梁体平均温度相比大气温度变化存在滞后性，单日平均温度变化不如大气温度变化显著。夏季与冬季大气温度变化显著，春季与秋季大气温度变化较小。

3 温度场测点分布规律

对于单箱三室箱梁而言，太阳辐射作用和大气散热作用错综复杂，以上作用可导致箱梁表面和内部产生较大温差，使混凝土发生开裂风险，因此对箱梁竖向温度和横向梯度展开分析。

3.1 箱梁竖向温度梯度

分别选取左腹板测点3、14、15、16、17、18、19、20、21的实测数据，左中腹板测点9、30、31、32、33、34、35、36、37的实测数据，右中腹板测点61、38、39、40、41、42、43、44、45的实测数据和右腹板测点67、82、85、86、87、88、89的实测数据进行分析，其中83、84传感器在夏季出现故障。以混凝土最底部为坐标原点，选取2021年8月5日(太阳辐射量最大)分别绘制两个边腹板及两个中腹板处的温度分布规律，如图10所示。

图10 腹板竖向温度时程分布曲线Fig.10 Time distribution curve of vertical temperature of the web

由图 10可知，受对流作用影响，两个中腹板测试数据[图10(b)、图10(c)]，除了最顶部测点和最底部测点，其余测点变化极小，单日最大温度变化为0.5 ℃。两个边腹板[图10(a)、图10(d)]各测点均产生较大的温度变化。受太阳辐射作用影响，向阳侧边腹板最大竖向温度梯度大于背阳侧[图10(a)、图10(d)]。向阳侧最大竖向温度梯度为13.3 ℃，背阳侧最大竖向温度梯度仅为4.2 ℃。

3.2 箱梁横向温度梯度

3.2.1 顶板横向温度梯度

分别选取1月14日和8月5日绘制夏季与冬季单箱三室箱梁底板横向温度梯度分布曲线，如图11所示。

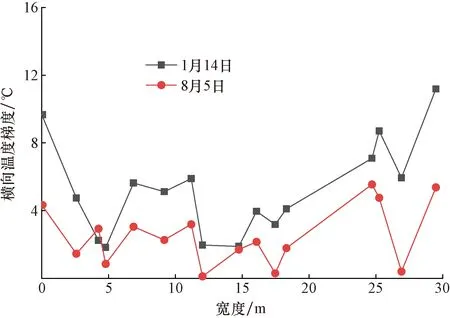
图11 夏冬季顶板温度梯度分布Fig.11 Temperature gradient distribution of summer and winter top plate

由图 11可以看出，夏季箱梁横向温度梯度最小于冬季横向温度梯度。以最右侧测点为例，夏季为5.372 ℃，而冬季达11.184 ℃。因此冬季顶板横向温度梯度大于夏季。

3.2.2 底板横向温度梯度

分别选取1月14日和8月5日绘制夏季与冬季单箱三室箱梁底板横向温度梯度分布曲线，如图12所示。

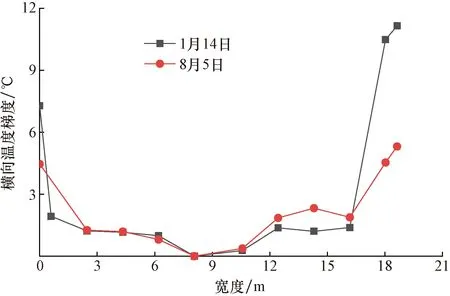
图12 夏冬季底板温度梯度分布Fig.12 Temperature gradient distribution of bottom plate in summer and winter

由图 12可以看出，由于冬季太阳高度较低，最大横向温度梯度值为12.0 ℃，大于夏季的4.7 ℃。底板的横向温度分布近似呈U形。根据目前现行的《铁路桥涵钢筋混凝土结构设计规范》(TB 10092—2017)(以下简称中国铁路规范)中对箱梁横向温度梯度的规定，如图13所示。

b为底板宽度；b1为翼缘板宽度；δ为顶板厚度；h为箱梁高度；T02为沿宽度方向的温度梯度；T01为沿高度方向的温度梯度图13 中国铁路规范箱梁温差分布图Fig.13 Distribution of temperature difference of standard box girder of Chinese railroad

由图13可以看出，中国铁路规范仅认为向阳侧存在温度峰值，其规定横向温度梯度计算公式为

Tx=T02e-ax

(3)

式(3)中：T02为沿宽度方向的温度梯度，取值为16 ℃；a为系数，取值为7 m-1；x为计算点至箱梁外表面的距离。

底板2020年1月14日横向温度梯度分布与中国铁路规范的对比，如图14所示。

图14 中国铁路规范-实测对比图Fig.14 Comparison of standard box girder of Chinese railroad and measured

由图 14可以看出，目前存在的中国铁路规范在横向温度梯度的计算上存在不足，特别是对于背阳侧的横向温度梯度效应存在明显误判：中国铁路规范认为背阳侧横向温度梯度趋近于0 ℃，而根据实测统计结果，底板背阳侧横向温度梯度为7.4 ℃，这是由于外界环境产生的热量使箱梁表面混凝土温度升高。

因此在考虑箱梁横向温度梯度时，还需考虑背阳侧表面混凝土的横向温度效应。筛选每日12：00—16：00向阳侧和背阳侧的温度梯度，横向温度梯度，如图15所示。

图15 横向温度梯度直方图Fig.15 Histogram of lateral temperature gradient

由图 15可知，背阳侧和向阳侧分别服从参数为W(1.359,2.372)和W(1.256,3.690)的Weibull分布。取温度作用代表值的重现期为50年，《公路桥涵设计通用规范》(JTG D60—2015)中规定桥梁的设计基准期为100年,则温度作用设计基准期内超过代表值的次数为2，超越概率为98%，分别计算得到实桥背阳侧、实桥向阳侧、模型背阳侧和模型向阳侧代表值分别为6.472 ℃和10.931 ℃。对式(3)进行改进，得

Tx=T02e-ax+T03e-a(b-x)

(4)

式(4)中：b为底板宽度，m；T03为背阳侧横向温度梯度，℃；a为系数。

针对本试验中实桥适用横向温度梯度计算公式为

Tx=10.931e-ax+6.472e-a(b-x)

(5)

3.2.3 腹板横向温度梯度

欧洲规范[24]指出，如果在大型混凝土箱梁桥梁的内/外腹板之间可能出现明显的温差，则在设计此类结构时需特别注意。由于冬季太阳高度角低，因此选取冬季向阳侧腹板温度梯度进行讨论。以测点83为例，测点83和测点75的温度差值为其横向温差。1月14日测点83、84、85、86和87处横向温差时程曲线，图16所示。

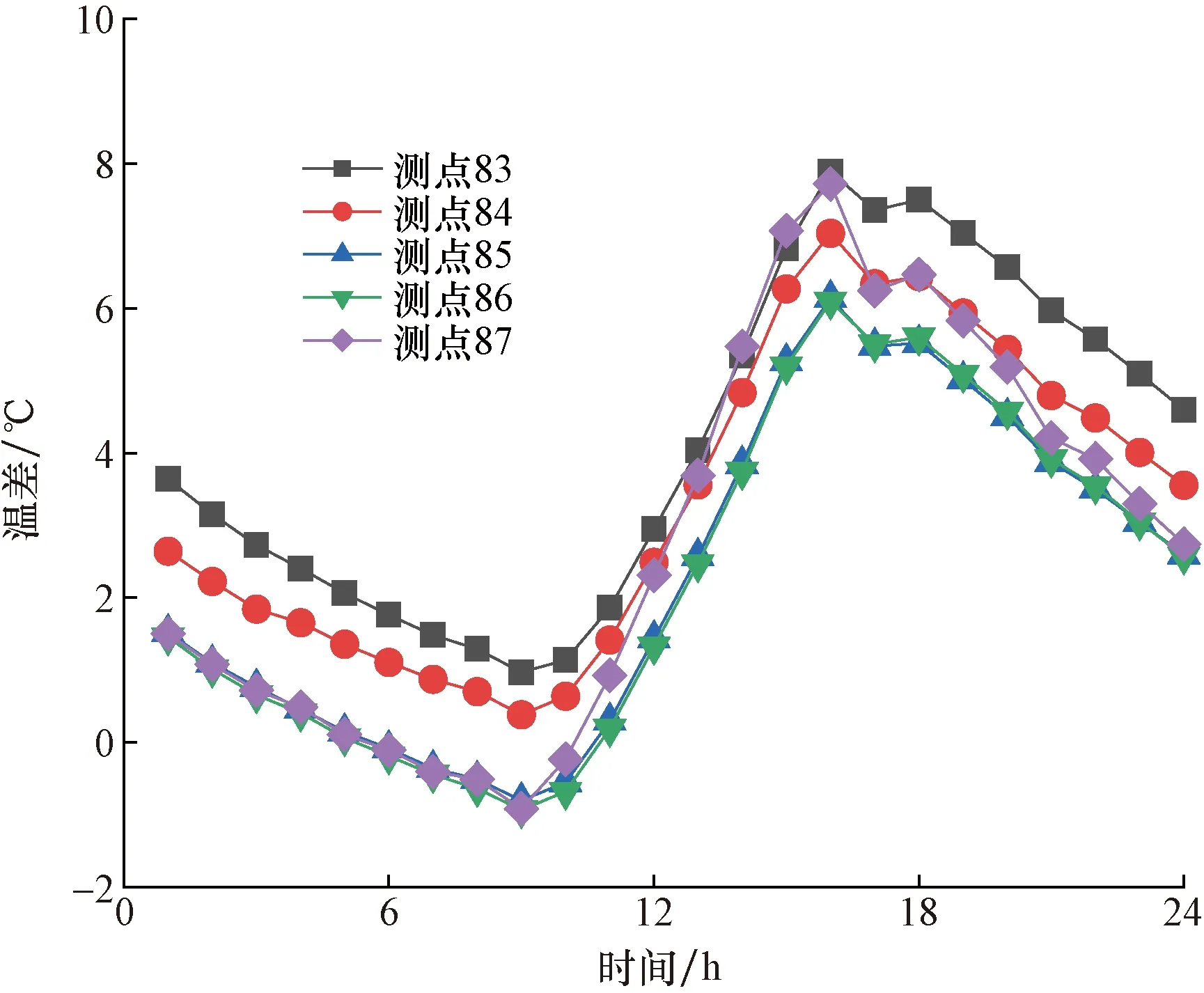
图16 横向温差分布图Fig.16 Distribution of lateral temperature difference

由图16可知，向阳侧腹板最大横向温差时刻出现在16时，最大值出现在测点83处，为7.9 ℃。不过沿腹板厚度仅有两排测点，需通过数值模拟进行准确分析。

4 有限元分析

4.1 材料属性设置

混凝土的比热容为单位质量混凝土温度升高1 ℃所需的热量，计算公式[25]为

C=∑piCi

(6)

式(6)中：pi为配合比各组分百分比；Ci为各组分比热。

混凝土热工参数如表1所示，计算得该模型的比热容为0.882 kJ/(kg·℃)。

表1 混凝土热工参数Table 1 Thermal parameters of concrete

4.2 边界条件设置

4.2.1 对流边界条件

根据第二类边界条件，混凝土箱梁各表面对流散热满足条件[1]为

箱梁顶板：hs=4.67+3.83v

(7)

箱梁底板：hs=2.17+3.83v

(8)

箱梁腹板：hs=3.67+3.83v

(9)

箱梁内壁：hs=3.5

(10)

式中：hs为对流换热系数；v为实测风速，m/s。

4.2.2 辐射边界条件

翼板对腹板有遮蔽作用，在建模过程中，需考虑翼板遮阴效果的影响[17]如图17所示。

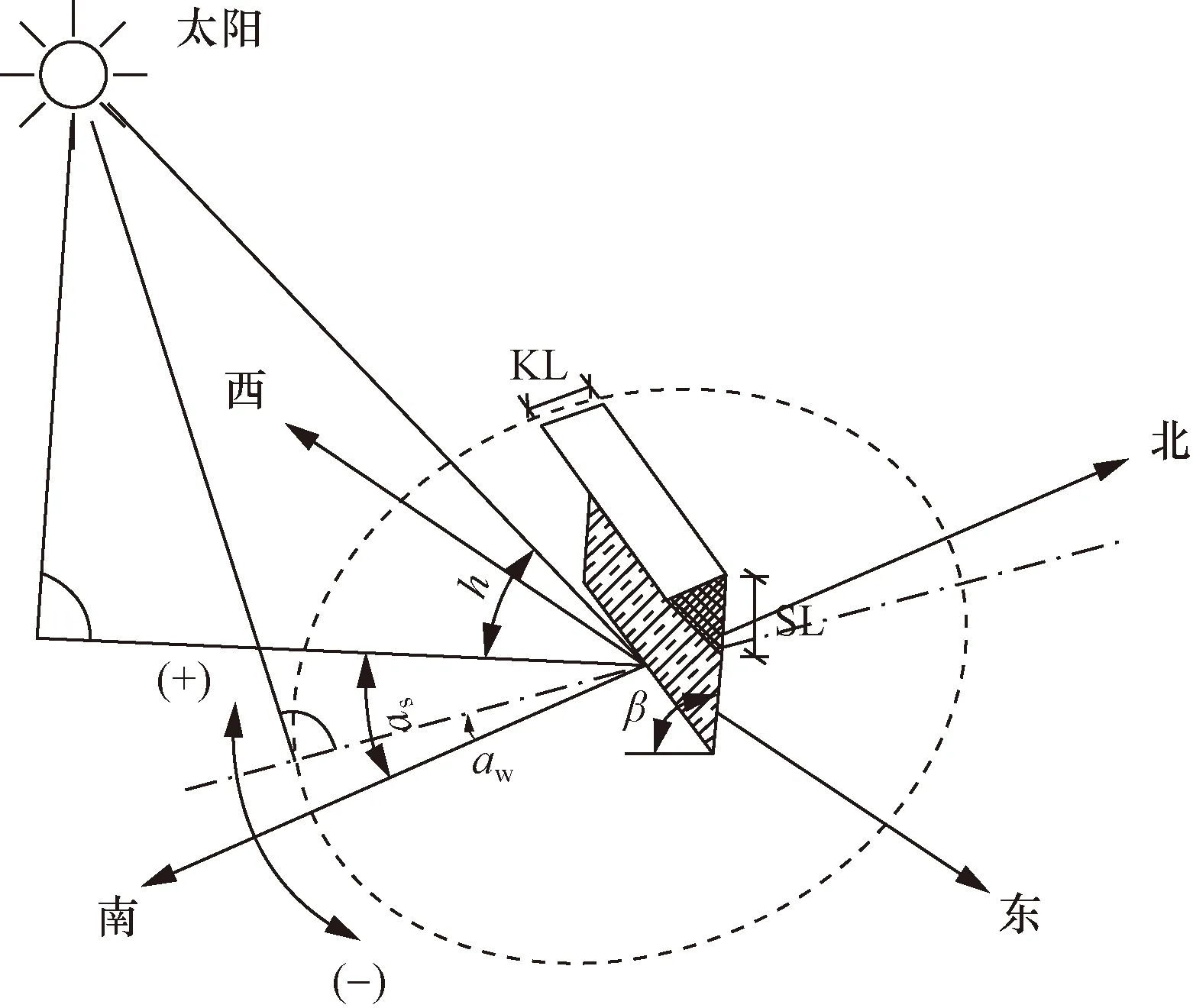
h为太阳高度角；aw为壁面方位角；as为太阳方位角；β为壁面与水平面的夹角(78°)；KL为悬臂长度(4.5 m)；SL为阴影长度图17 翼板对腹板遮阴作用Fig.17 Shading effect of the airfoil on the web

太阳时角τ可由当地时间进行计算，公式为

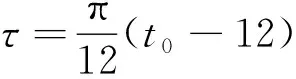
(11)

式(11)中：t0为当地时刻，h。

太阳赤纬δ可由式(12)进行计算，公式为

(12)

式(12)中：D为一年中计算日的天数；dspr为当年春分距离当年元旦的时间,d。

太阳高度角θ可由式(13)进行计算，公式为

θ=arcsin(sinψsinδ+cosψcosδcosτ)

(13)

式(13)中：ψ为当地的纬度，取桥址纬度为109°。

壁面方位角as可由式(14)进行计算，公式为

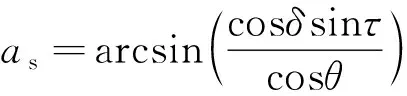
(14)

阴影高度可由式(15)进行计算，公式为

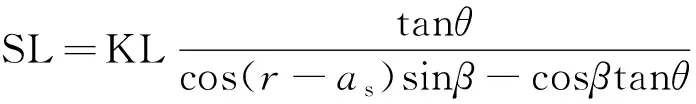
(15)

式(15)中：r为桥梁外法线方向角，取20°。

以16点为例，绘制2021年全年的腹板遮阴长度分布图，如图18所示。

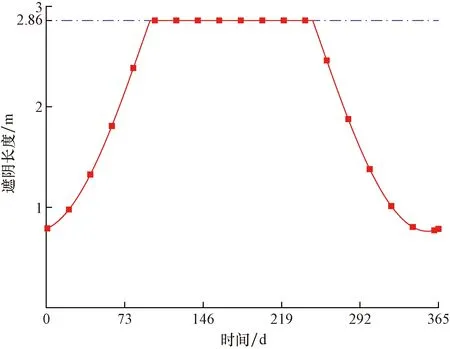
图18 全年16：00遮阴长度分布图Fig.18 Distribution of shade length at 16：00 throughout the year

由图18可知，在全年的第96～246天(2021年4月7日—9月4日)，向阳侧腹板16：00均被翼缘板阴影覆盖，在其他日期内，向阳侧腹板最底部测点均会在16：00被太阳直射。因此针对遮阴处和直射处需分开讨论。以1月14日为例，将实测太阳辐射和太阳散射数据施加到边界上，如图19所示。

图19 太阳直射-散射关系图Fig.19 Solar direct-scattering relationship

4.3 单元尺寸划分

采用DIANA软件建立数值模型，共划分10 572个HX24L实体单元，热边界划分3 960个BQ4HT对流边界单元。在热边界上输入大气温度时程曲线。

4.4 数值模型验证

分别计算1月14日和8月5日温度场分布状态。以8月5日为例，选取顶板(测点67)、底板(测点45)、向阳侧(测点85)与背阳侧(测点17)实测值与计算值进行对比，如果如图20所示。

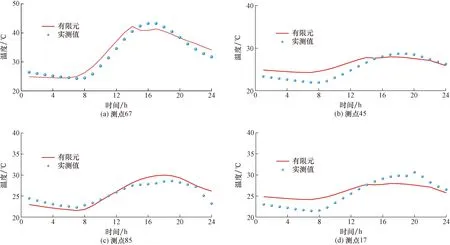
图20 理论-实测对比图Fig.20 Theoretical-measurement comparison chart

由图20可以看出，图20(a)～图20(d)的实测值与计算值的决定系数R2分别为0.940、0.899、0.913和0.929，数值模拟的结果对实测温度预测准确，证明有限元结果与单箱三室箱梁全截面温度测试结果吻合。

分别绘制1月14日和8月5日20时温度场分布云图，如图21和图22所示。

图21 1月14日温度场分布云图Fig.21 Cloud map of temperature field distribution on January 14th

图22 8月5日温度场分布云图Fig.22 Cloud map of temperature field distribution on August 5th

由图21和图22可知，由于夏季太阳辐射高于冬季，夏季竖向温度梯度明显大于冬季。以20：00为例边腹板最大竖向温度梯度分别为12.4 ℃和5.3 ℃。由于冬季太阳高度角低于夏季，腹板横向温度梯度明显大于夏季。选取向阳侧腹板，绘制夏季和冬季腹板横向温差曲线图，如图23所示。

图23 向阳侧腹板横向温度时程曲线图Fig.23 Time course graph of transverse temperature of sunny side webs

由图23可知，腹板中点处在冬季和夏季被太阳直晒的时间分别为16：00和18：00，由于太阳直射作用大于太阳散射，因此冬季外表面温度峰值出现在16：00，夏季外表面峰值出现在18：00。冬季腹板最大横向温度梯度峰值出现在16：00，为12.8 ℃，夏季腹板最大横向温度梯度峰值出现在18：00，为5.07 ℃。说明温度峰值出现在腹板受太阳直射时，辐射值最大的时刻，而非太阳辐射最大的14：00。

5 结论

在王家河特大桥桥址放置了混凝土箱梁温度场监测模型，在箱梁截面上埋设大量温度测点，实现了箱梁全截面的二维太阳辐射温度场实时测量，在被测截面上建立局部坐标系，得到结论如下。

(1)太阳辐射测试结果存在季节性，夏季太阳辐射强烈。风速测试结果无季节性特征。箱梁平均温度在夏季和冬季变化较大，分别为5.2 ℃和4.1 ℃，平均温度的每日最值可用大气温度进行估计。

(2)受对流作用影响，中腹板除顶底部测点外变化极小可被忽略。受太阳辐射作用影响，向阳侧边腹板竖向温度梯度大于背阳侧竖向温度梯度。夏季竖向温度梯度大于冬季温度梯度。

(3)受太阳高度角影响，冬季向阳侧照射时间比夏季长。冬季箱梁最大横向温度梯度为12.0 ℃，大于夏季的4.7 ℃。

(4)箱梁横向温度梯度呈U形分布，背阳侧横向温度梯度的98%超越概率值为6.472 ℃。基于向阳侧和背阳侧温度梯度首次提出基于中国铁路规范的修正公式。

(5)建立考虑遮阴长度的温度场模型，揭示了向阳侧腹板横向温度梯度冬季大于夏季的原因。