连续管注入头与滚筒液压系统的耦合动力学

李银银，周志宏,*，曾华，王汤

(1.长江大学机械工程学院，荆州 434023； 2.中石化江汉石油工程有限公司页岩气开采技术服务公司，武汉 430000)

连续管可带压连续作业，装置具有占地面积小、作业效率高、搬迁安装方便等诸多常规作业机不具有的优点，广泛应用于油气开采的各个领域[1-2]。连续管平时储存在滚筒上，作业时从滚筒上展开，经鹅颈导向器和注入头注入井中，或者由注入头从井中起升，经鹅颈导向器导向滚筒，再由滚筒卷绕到滚筒上[3-4]。在注入头和滚筒之间的连续管必须有一定的张力，保证连续管的有序展开或卷绕整齐。张力不能太小，否则可能造成乱管[5]；也不能太大，太大会造成中性层偏移，影响连续管的疲劳寿命[6]。连续管注入头和滚筒都采用液压马达经减速器驱动，注入头和滚筒各自形成一个相对独立的子系统，经过连续管将二者的运动状态联系起来。注入头和滚筒的运动状态对它们之间的连续管的张力有很大的影响。如果张力变化幅度过大，可能产生张力过载，造成连续管的损伤；如果张力产生一定频率的振动，有可能激起连续管的共振，造成连续管的损伤[7]。

近几年来，研究人员对注入头与滚筒间的连续管的张力进行了研究。彭嵩等[8]研究和设计了连续管测井机注入头液压系统，解决注入头与滚筒协同控制问题；张建庆[9]研究了注入头和滚筒间液压同步的问题；杨高[10]、刘平国等[11]研究了滚筒液压系统的溢流压力控制张力的问题；刘远波等[12]、段文益等[13]通过将滚筒液压系统改成电液来解决张力控制的问题；马卫国等[14]则通过MATLAB模拟滚筒液压系统来分析张力的变化问题。但目前所有的研究均未考虑注入头液压系统、滚筒液压系统之间的动力耦合以及在作业中动力参数的变化对张力的影响。

实际上，注入头-滚筒-连续管构成了一个动力系统，注入头和滚筒的液压系统是其中的子系统。在这个系统中任何一个子系统的状态变化将会影响到另一个子系统的状态。现通过有限元及MATLAB/Simulink软件，建立连续管注入头与滚筒液压系统的耦合动力学模型，考虑注入头液压系统、滚筒液压系统之间的动力耦合以及在作业中动力参数的变化对连续管上张力的影响，分析不同操作速度下，满滚筒和空滚筒起升注入过程中连续管上张力变化情况，解决导向器与滚筒之间连续管的张力过载及管体振动问题，为连续管注入头与滚筒液压系统设计及作业提供指导。

1 注入头和滚筒液压系统

注入头的液压系统原理图如图1所示。

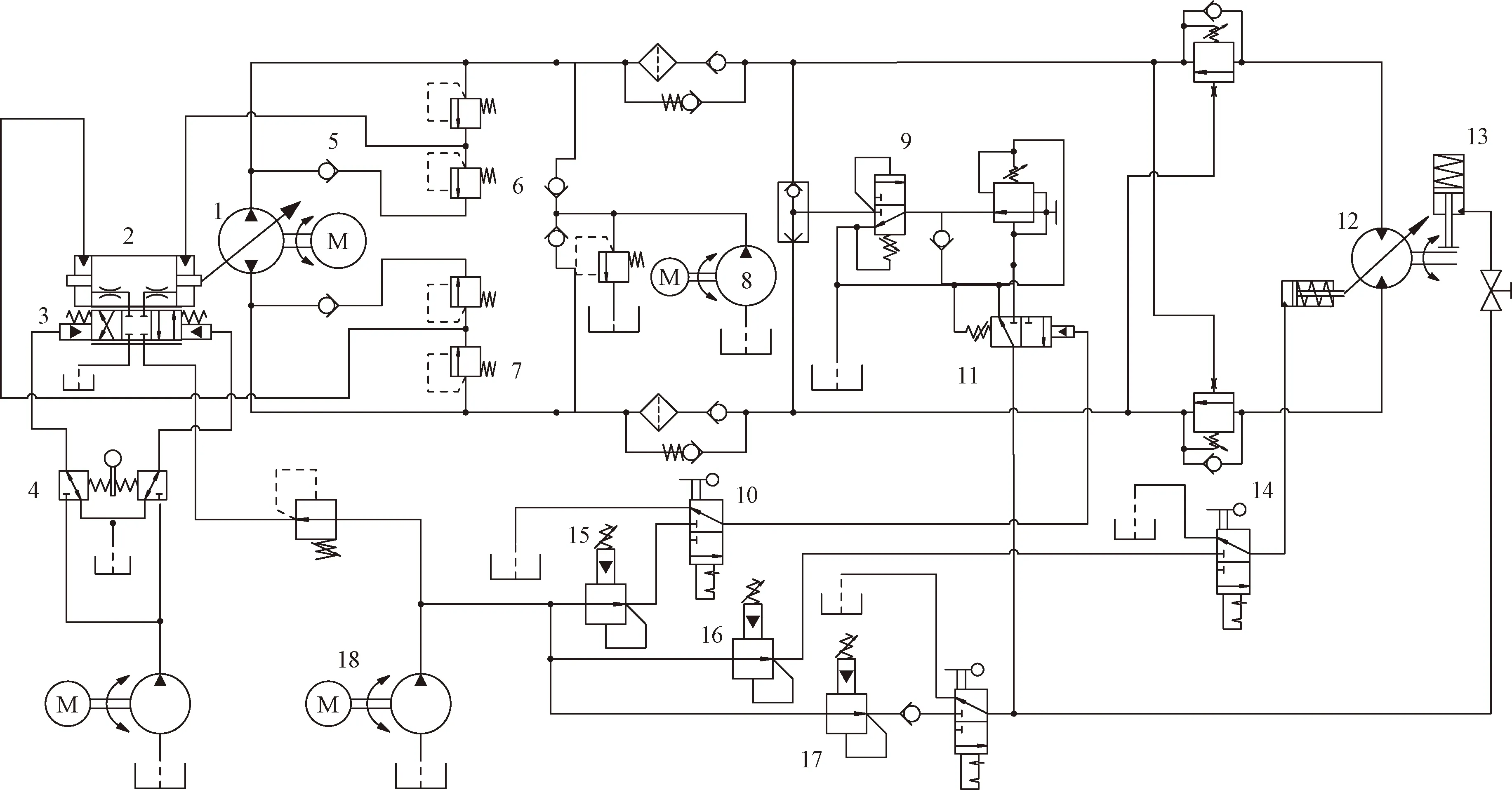
1为变量泵；2为液缸；3为三位四通阀；4为比例阀；5为单向阀；6，7为溢流阀；8，18为液压泵；9为跟随阀；10为控制阀；11为液动换向阀；12为液压马达；13为刹车液缸；14为手动控制阀；15，16，17为减压阀；M代表电机图1 注入头液压系统原理图Fig.1 Schematic diagram of hydraulic system of injection head

注入头液压系统的工作原理如下：注入头由变量泵驱动双速变量马达，变量马达可以在高速和低速两档之间更换，在高速档或低速档时，都可以通过控制台的阀的控制变量泵输出不同流量供给液压马达实现注入或起升连续管的两档中的速度调节。注入头的液压马达上有常闭式刹车，不工作时，刹车的液压回路没有压力油，刹车在弹簧的压力下刹住液压马达的轴，工作时，液压油进入刹车回路，使刹车打开。变量泵1和液压马达12组成闭式主回路，液压泵8为闭式液压系统补油。液压泵18提供控制系统的液压油，通过减压阀15和控制阀10将刹车先导油导入阀11，接通阀11，如果变量泵1没有启动，通过减压阀17的压力油通过阀11，和单向阀进入阀9后直接回油箱，刹车依然无法开启；如果变量泵1启动了，高压端通过梭阀迫使阀9关闭通往油箱的油路，连通变量泵的高压回路，高压油将进入刹车液缸13，打开刹车。通过减压阀16和手动控制阀14来控制液压马达的高低速档。

在高速或低速挡位上进一步的速度控制通过控制变量泵的流量来实现。改变变量泵的斜盘的角度就可以调节变量泵的排量，斜盘的角度由液缸2的活塞来推动。为了保证液缸活塞能按确定的要求推动斜盘，三位四通阀3的阀壳体与控制活塞相连，当比例阀4的动作使三位四通阀右边压力高时，其阀芯向左运动，接通右边的阀位，液缸右边充压，带动活塞向左运动，阀壳体跟随运动，使活塞回到中间的阀位，反之亦然。当变量泵1压力下面高时，如果压力超过允许的压力，通过溢流阀7，使压力油进入液压缸2左边的腔中，腔中压力液推动活塞运动，将右边腔室的液压油通过溢流阀6和单向阀5挤回泵的低压回路中。

滚筒的液压系统相对于注入头来说比较简单，如图2所示。主回路采用开式油路，由主油泵供油给马达，滚筒的正反转采用换向阀变换动力液的方向，从而控制滚筒的正转和反转。安装在操作台上的远控溢流阀，通过对此阀的调节，可使回路压力在0～17.5 MPa 调节，进而控制滚筒的转矩来控制连续管的张力。

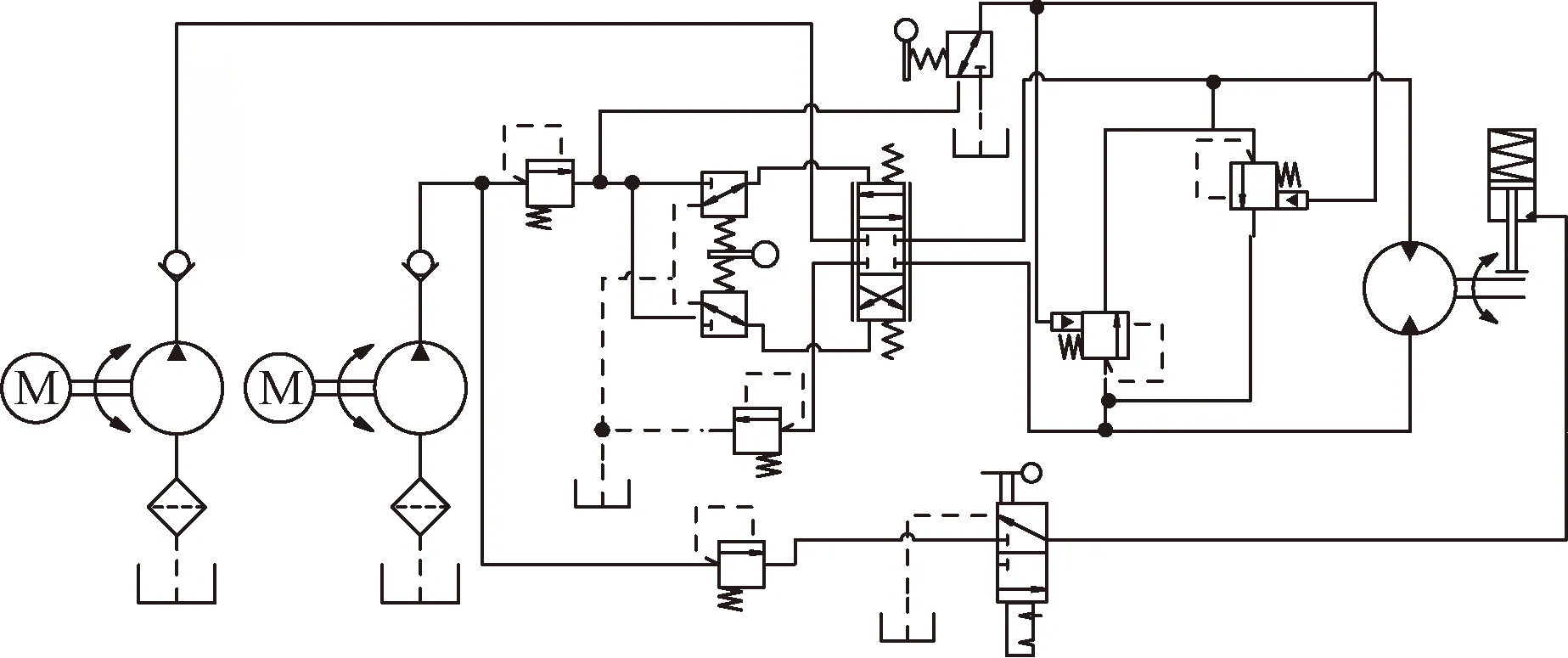
图2 滚筒液压系统原理图Fig.2 Schematic diagram of hydraulic system of reel

2 滚筒与导向器间连续管张力分析

定义滚筒与鹅颈导向器间连续管的松弛度R为实际连续管长度与完全绷紧状态的差。这样滚筒与鹅颈导向器间连续管的张力T与松弛度R就存在一定的函数关系，采用有限元来计算张力与松弛度的关系。为了减少计算规模，在与滚筒和鹅颈导向器相接触的部分连续管用三维模型，而在没有接触的地方用梁单元，如图3所示。

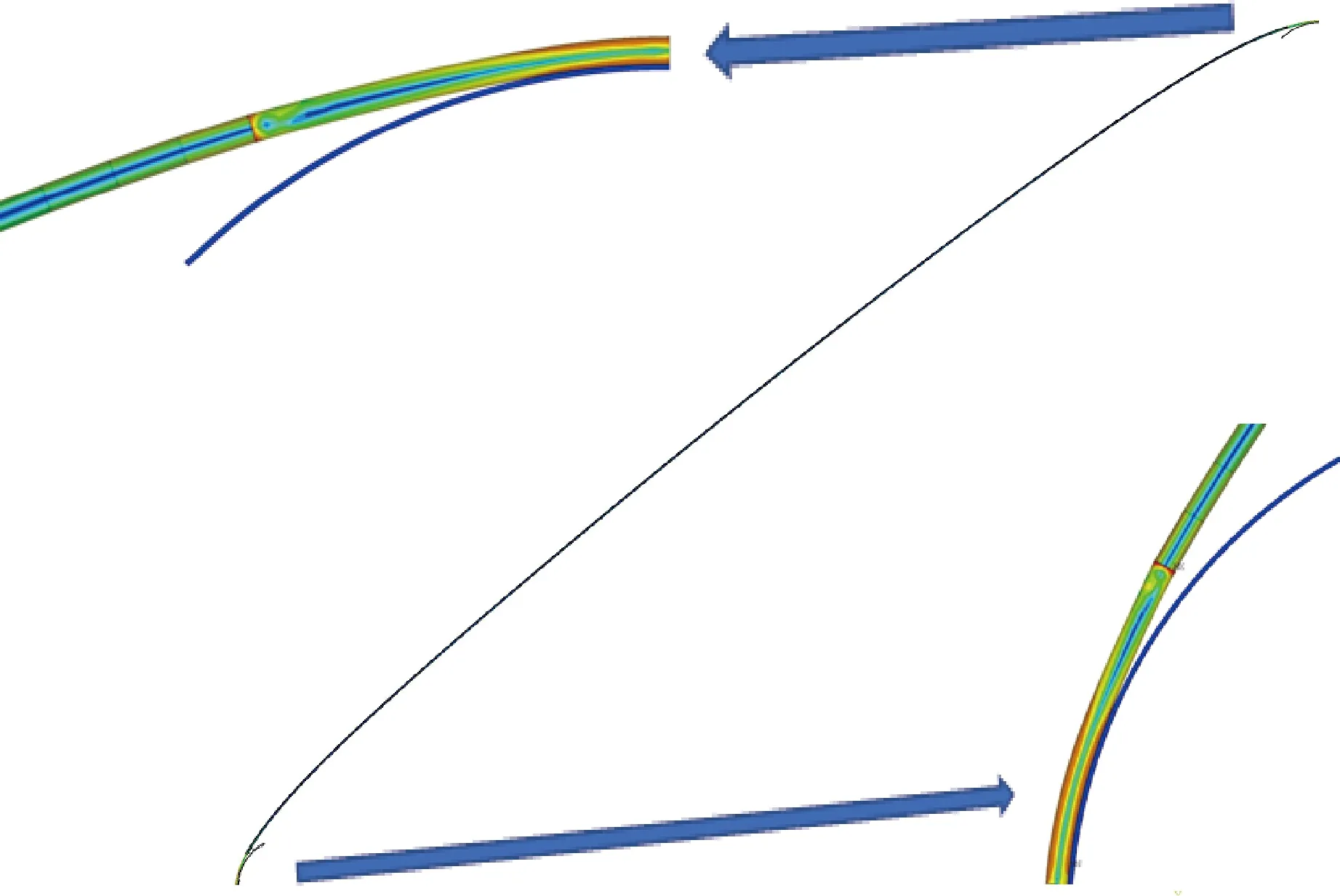
图3 有限元模型计算结果与细节Fig.3 Calculation results and details of the finite element model

在计算中，固定滚筒的位置，移动鹅颈导向器逐步连续管张紧，可计算出张紧力与松弛度之间的关系。以QT900钢级，外径为50.8 mm、壁厚为4.445 mm的连续管为例，假设滚筒边缘与鹅颈导向器顶部的水平距离25 m，滚筒中心到鹅颈导向器顶部的垂直距离为20 m。用有限元计算出松弛度大于零的张力，考虑到连续管的张紧程度有可能超过绷直的情况，即松弛度为负，连续管处于拉伸变形，可拟合出函数关系式(1)，拟合曲线如图4所示。

图4 滚筒与鹅颈导向器间连续管张力与松弛度之间的关系Fig.4 Relationship between tension and relaxation of the coiled tubing between reel and gooseneck guide

(1)

式(1)中：R为松弛度，mm；T为张紧力，N。其他单位已包含在拟合常数中。

3 注入头与滚筒液压系统的耦合模型

注入头-滚筒-连续管构成了一个动力系统，注入头与滚筒液压动力系统通过之间的连续管耦合在一起。当启动注入头注入连续管或是起升连续管，一般将连续管加速直到设定的速度；当运动的连续管需要停止时，连续管就会减速直到静止，这些过程涉及动力响应，加速或减速的时间长短非常重要。另外，在运行过程中这些系统中的动力参数也在变化，例如滚筒上卷绕的连续管的长度不一样，转动惯量不一样。同样，下入到垂直井中的连续管长度不一样，注入头夹持的连续管的惯性也不一样。因此系统表现的动力特征也不一样，由惯性效应产生张力变化也有很大的差别。用Simulink建立注入头与滚筒液压系统的耦合的动力学模型，如图5(a)所示，其中的T-R model模块如图5(b)所示。

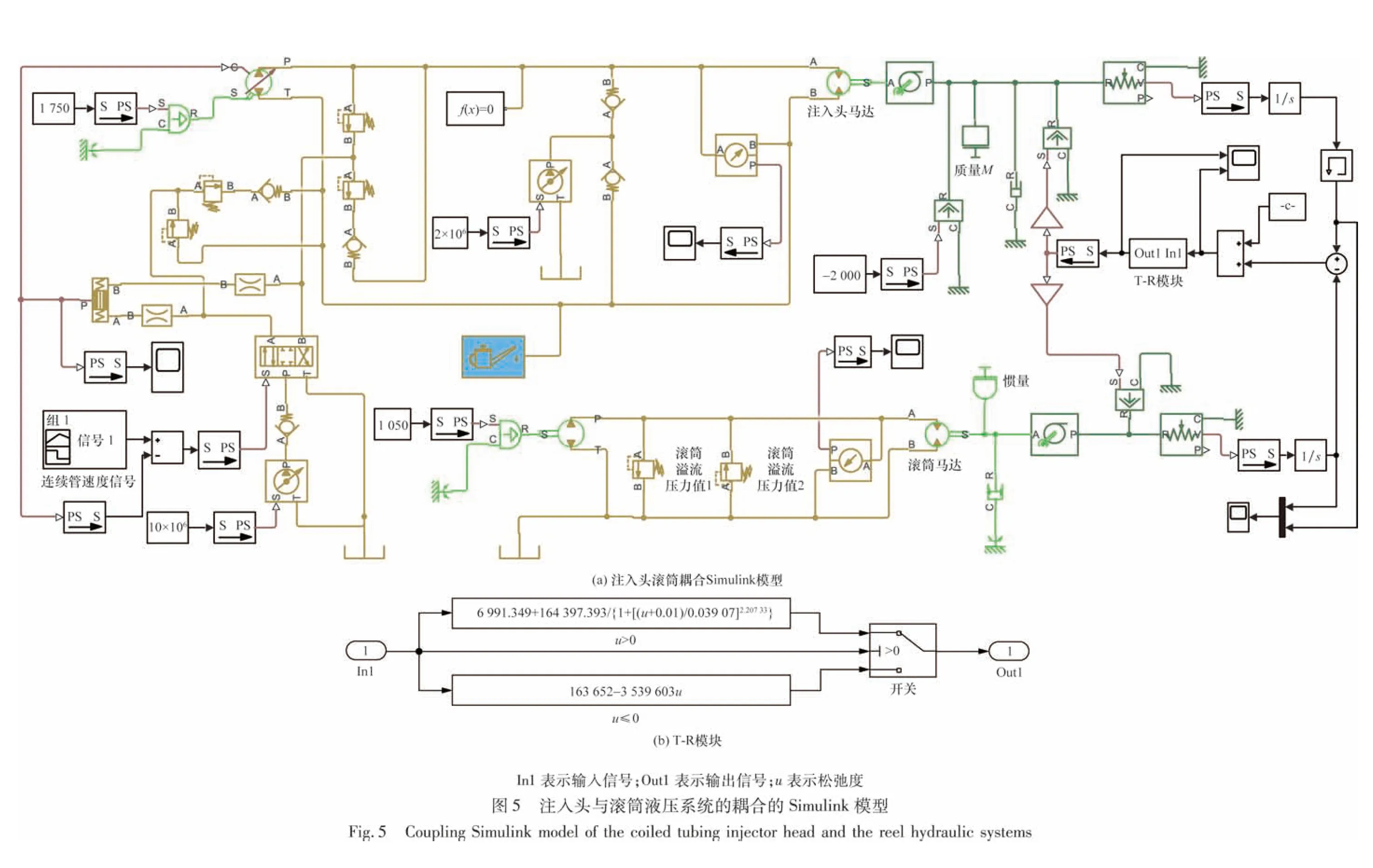
在运行过程中，影响系统的参数主要是惯性和滚筒液压系统的溢流压力。注入头动力部分的质量主要是悬垂于井中的连续管，在图5(a)中用M来表示，这部分质量还产生了向下的重力。滚筒的转动惯量包括滚筒和滚筒上的连续管的转动惯量，图5(a)中的“惯量”，设置时满滚筒时为89 000 kg·m2，滚筒上仅缠绕一层连续管时，约为1 700 kg·m2。假设滚筒的减速比100，折算在滚筒液压马达轴上的转动惯量分别是8.9 kg·m2和0.17 kg·m2。滚筒的液压压力由溢流阀设置，可通过司钻台远程控制，滚筒溢流压力分别设置为5 MPa和10 MPa。

4 计算结果

在模拟时，连续油管的张力依靠滚筒马达的溢流阀维持马达的反扭矩，即图5(a)中的滚筒溢流压力值1和滚筒溢流压力值2。连续油管的注入速度和起升速度依靠连续管速度信号模块提供信号，假设加减速均为匀加减速。图6(a)所示的是起升过程，在第14秒开始加速，1 s加速到最大速度；第40秒开始减速，1 s内减到零。图6(b)所示的是注入过程，第14秒时开始加速注入，1 s内以匀加速到最大注入速度；第40秒开始减速，1 s内以匀减速使注入速度为零。在计算中，假设加减速时间为0.1、1、3 s。

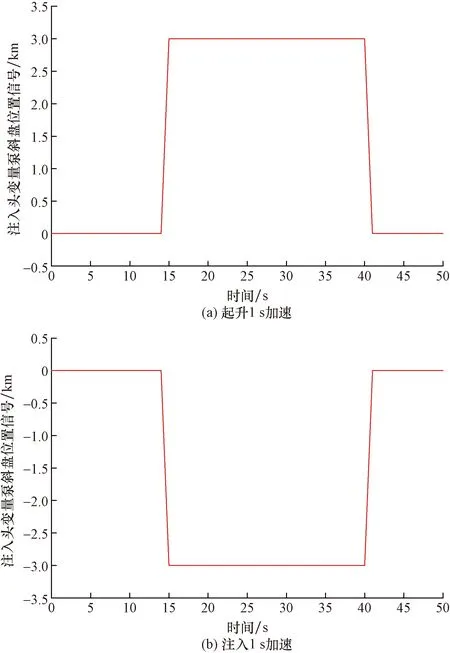
图6 注入头变量泵输入信号Fig.6 Input signal of injector head variable displacement pump

4.1 满滚筒起升

设连续管的最大起升速度为1 m/s，处于满滚筒状态，滚筒的溢流压力为5 MPa或10 MPa，操作起升速度从0到最大起升速度的时间为参数，连续管松弛度和张力随时间的变化如图7所示。

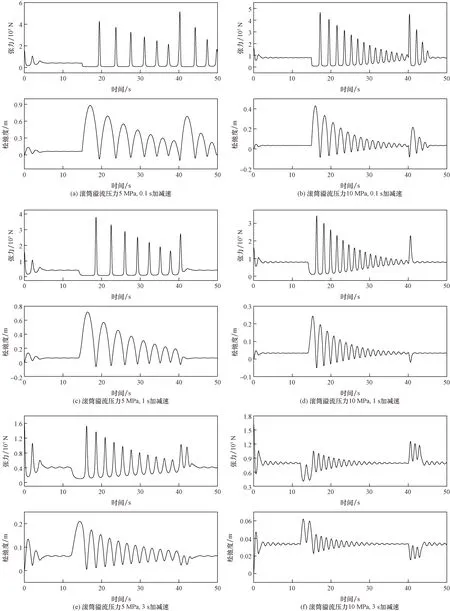
图7 起升时滚筒惯性矩89 000 kg·m2的松弛度与连续管张力Fig.7 Relaxation and tension of the coiled tubing when inertia moment of reel is 89 000 kg·m2 during lifting

在注入头加速期间，滚筒的加速度来不及跟上注入头的加速度，导致连续管的松弛度增加，与作业现场滚筒和导向器之前连续管松弛现象一致[15]。加速时间越长，加速度越小，产生的松弛度和张力的变化越小。如果滚筒溢流压力设定为5 MPa，当加速时间为0.1 s时，连续管有一段时间的松弛，松弛度达0.9 m，然后连续管张力迅速升至400 kN以上，形成过载；可以看出，如果滚筒溢流压力设定为10 MPa，虽然松弛度只有0.4 m，但连续管张力仍然高达450 kN，过载严重。如果缓慢加减速，例如用3 s加减速到最大速度时，张力只达到150 kN。

4.2 满滚筒注入

设连续管的最大注入速度1 m/s，处于满滚筒状态，滚筒的溢流压力为5 MPa或10 MPa，操作起升速度的手柄从0 m/s到最大起升速度的时间为参数，连续管松弛度和张力随时间的变化如图8所示。很明显，在注入头加速期间，滚筒的加速度来不及跟上注入头的加速度，导致连续管的松弛度增加，加速时间越长，加速度越小，产生的松弛度和张力的变化越小，最低加速时间不能低于3 s。

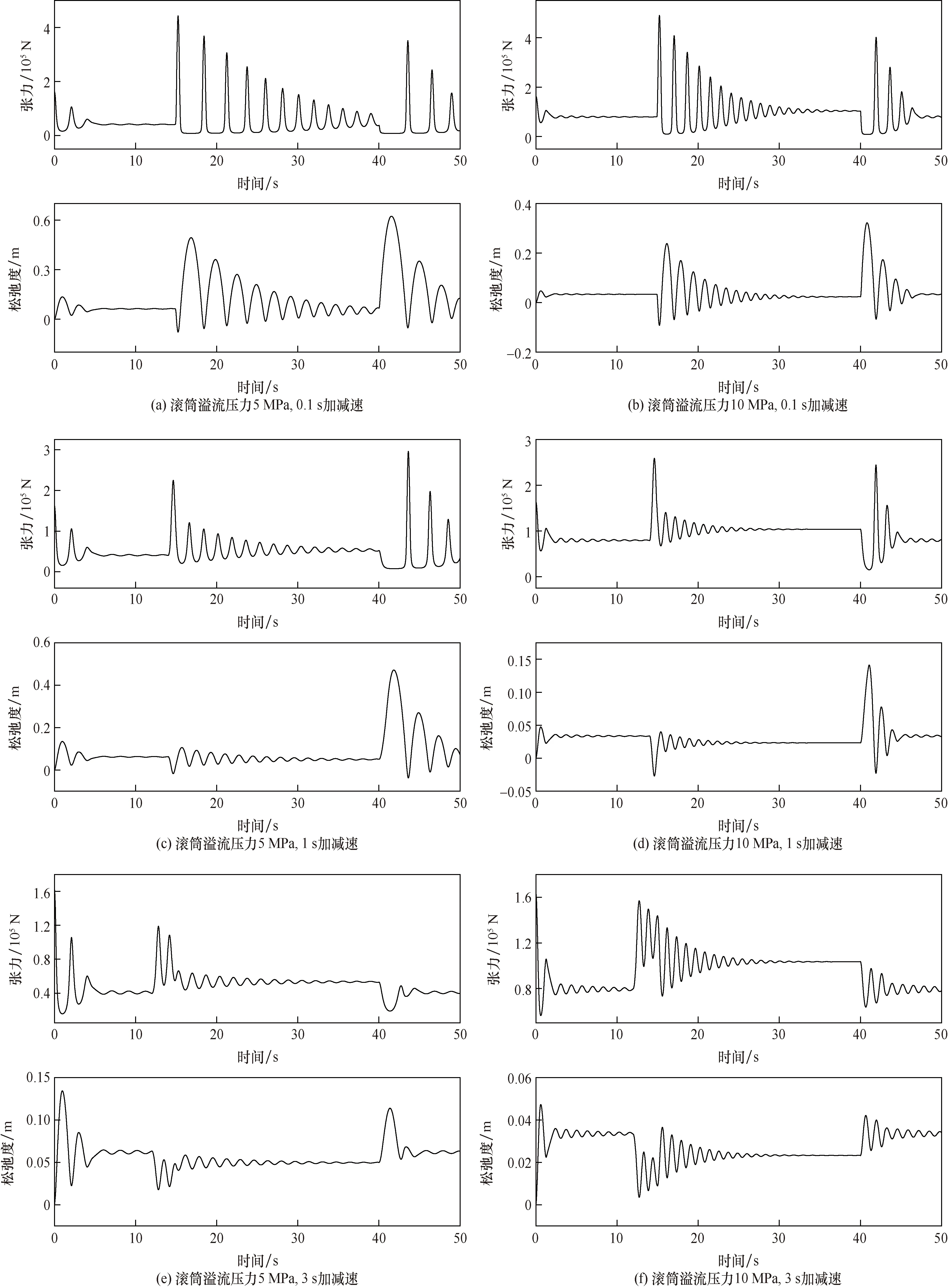
图8 注入时滚筒惯性矩89 000 kg·m2的松弛度与连续管张力Fig.8 Relaxation and tension of the coiled tubing when inertia moment of reel is 89 000 kg·m2 during injecting

4.3 空滚筒注入与起升

设连续管的最大注入速度1 m/s，当滚筒上只有少量的连续管，滚筒转动惯量为1 700 kg·m2，滚筒的溢流压力为5 MPa或10 MPa，操作起升速度的手柄从0 m/s到最大起升速度的时间为参数，连续管松弛度和张力随时间的变化的细节如图9所示。很明显，发生了较长时间的张力振动，滚筒溢流不同，振动的频率不同，溢流压力越大，频率越高。在连续管作业现场，当操作引起的振动的频率与连续管故有频率接近时，将引起导向器与滚筒之前的连续管发生共振。

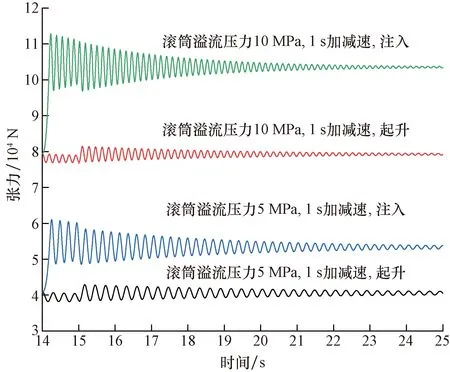
图9 滚筒惯性矩1 700 kg·m2的连续管张力Fig.9 Tension of the coiled tubing when inertia moment of reel is 1 700 kg·m2

5 结论

针对注入头液压系统与滚筒液压系统的耦合动力学进行了研究，得出以下结论。

(1)所提出的模型可以很好地模拟注入头液压系统与滚筒液压系统的耦合动力学问题。

(2)当滚筒上卷绕大部分连续管时，滚筒惯性很大，如果操作连续管注入和起升时过于猛烈，容易造成连续管张力变化过大，如果张力过小，会乱管；如果张力过大，会造成连续管的损伤。建议缓慢加速或减速，加减速时间不得小于3 s。

(3)在滚筒仅卷绕一层左右连续管时，操作连续管加减速可能导致较长时间的耦合振动，如果与连续管的固有频率接近，将产生系统共振。