基于PSO-ELM的水平井自喷期“多段式”产量预测方法——以玛湖油田百口泉组致密砾岩油藏为例

王林生，黄长兵，朱键，覃建华，张景，李文涛

(1.中石油新疆油田公司，克拉玛依 834000； 2.西南科技大学固体废物处理与资源化教育部重点实验室，绵阳 621010； 3.新疆油田公司勘探开发研究院，克拉玛依 834000)

随着生产时间的推移，水平井单井产量递减特征更为清晰，掌握其递减规律，对油藏管理和生产规划具有重要的意义。由于致密砂砾岩储层非均质性强，物性纵横向变化，渗流规律极其复杂，综合导致产量预测难度极大[1]。目前传统的水平井产量预测方法主要是公式法和数值模拟法[2]，但无论是公式法还是数值模拟法，均需要利用早期的生产数据进行拟合再进行预测。由于水平井产量受储层环境、后期改造等多种因素的影响，呈“多段式”生产特征，而传统预测方法主要基于理论模型，参数选取主要依靠经验，容易受短期生产特征的影响，预测结果误差大，难以满足实际需求[3-5]。

近年来，随着人工智能技术的飞速发展，机器学习方法在单井产量预测方面得到了越来越广泛的应用[6]。纪天亮等[7]利用反向传播(back propagation，BP)神经网络预测水平井产能，得到了较好的应用效果。陈娟等[8]在BP神经网络初始权值和阈值计算中，利用遗传算法进行优化，应用在页岩气水平井产量预测中，预测精度明显提高。陈浩等[9]基于支持向量机建立致密油藏水平井产量预测模型，并在参数选取方面分别利用常规式和嵌入式进行优化，应用于大庆油田水平井产能预测中，预测效果明显优于BP神经网络模型。张蕾等[10]提出了基于时域卷积神经网络模型的水驱油田单井产量预测方法，进一步提高了水平井单井产量预测精度。然而，传统的机器学习法由于需要人为设置参数，在计算速度和适用性方面，仍存在一定的不足。现根据玛湖油田水平井生产“多段式”特点，充分结合实际生产资料，利用主成分分析法优选主控因素，并最终提出利用粒子群优化的极限学习机法，建立水平井产量预测模型。相较于传统机器学习法，该方法具有计算速度快，预测结果可靠性高等优点[11]，以期为致密砾岩油藏水平井产量预测提供指导。

1 玛湖油田水平井生产概况

玛湖油田百口泉组发育斜坡背景下的大规模浅水扇三角洲沉积，储层主要发育在河道和砂坝中，储集岩体砂砾岩叠置连片，储层致密，属于典型的致密砾岩储层。为了提高单井产量，研究区水平井主要采用大段多簇、极限限流射孔、段内暂堵压裂工艺。自喷期实际具有波动稳产或波动递减的特征，因为此阶段地层能量相对较高，每当产量下降到一定程度，采油管理单位就会采取钻塞、冲砂、放大油嘴等措施维持产量。MaHW1325井与MaHW6112井自喷期产量变化图像如图1所示。

图1 MaHW1325井与MaHW6112井自喷期产量Fig.1 Production of MaHW1325 well and MaHW6112 well during the self-injection period

由产量图像分析可知，玛湖油田水平井自喷期的产量受地层环境以及压裂工艺等因素影响，具有典型的多段式递减的特征，这也导致常规的公式或者数值模拟很难准确预测水平井单井产量。

2 主控因素分析和评价

2.1 水平井自喷期产量主控因素分析

玛湖油田致密砾岩储层水平井自喷期产量受到多种因素的影响，主要包括：①储层物性参数，如孔隙度、渗透率、含油饱和度等；②油藏基本条件，如油压、油层厚度等；③水平井压裂参数，如水平段长度、井距、压裂簇数、簇间距、总液量、加砂量等。由于玛湖油田水平井实际生产仪器、技术等限制，只能得到部分生产资料，在已有的数据资料中，选择水平井自喷期产量主控因素。表1为研究区随机选取的15口水平井自喷期产量数据。

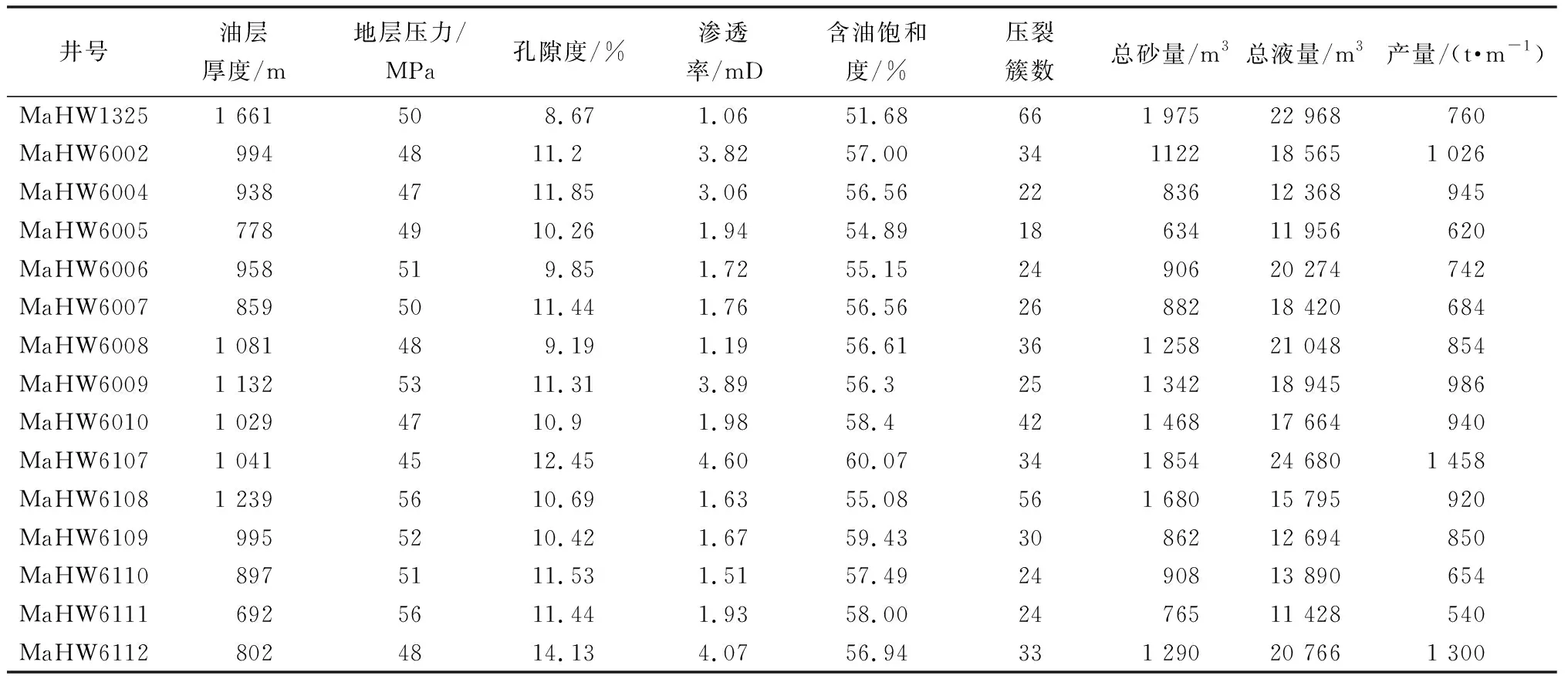
表1 研究区选取的15口水平井自喷期产量数据Table 1 Production data of 15 horizontal wells selected in the study area during flowing period

2.2 主控因素选取评价

在建立水平井产量预测模型过程中，主控因素的选择尤为关键，参数选择过多、过少，都会影响预测模型效率以及结果的可靠性。因此，在模型参数选择方面，一定是尽可能选取与预测结果相关性较高的影响因素。主成分分析法(principal component analysis, PCA)，通过“降维”的思想，在多元数据分析中，利用变量之间的相关性，结合统计分析法在多个变量中提取几个主成分，从而降低问题复杂性和难度，在主控因素评价方面有着广泛应用[12]。本文采用主成分分析法，用来判断各影响因素与产量的相关性，结果如表2所示。

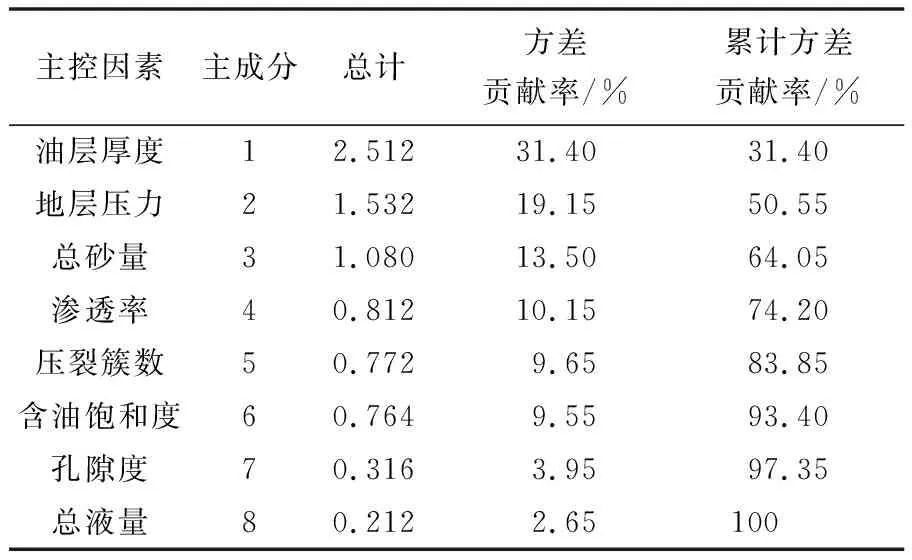
表2 主成分分析结果Table 2 Results of principal component analysis

根据累积方差贡献率大于85%，选取油层厚度、地层压力、总砂量、渗透率、压裂簇数、含油饱和度6个因素作为输入参数，建立水平井产量预测模型。

3 PSO-ELM模型原理

3.1 ELM原理

极限学习机(extreme learning machine，ELM)作为一种有监督学习，对比其他机器学习算法，具有所需训练参数少、学习速度快、泛化能力强等优点，在数据预测方面有着良好的表现[13]。极限学习机是一种单隐层前馈神经网络，选用极限学习机结构模型如图2所示。

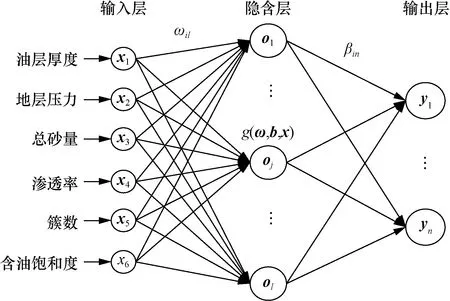
图2 极限学习机结构图Fig.2 Support vector machine structure diagram

极限学习机算法原理：n个训练样本(Xi，Yi)，输入为Xi=[xi1,xi2,…,xin]T，输出为Yi=[yi1,yi2,…,yin]T，隐含层节点个数为l，激活函数为g(x)，输入层与隐含层连接权值为ωi=[ωi1,ωi2,…,ωin]T，隐含层与输出层连接权值为βi=[βi1,βi2,…,βin]T，隐含层偏置为bi=[bi1,bi2,…,bil]T。极限学习机算法表达式为

Y=Hβ

(1)

式(1)中：H为隐含层输出矩阵，表示为

通过求式(2)方程组最小二乘解，确定隐含层与输出层连接权值为

(2)

3.2 PSO优化ELM参数

由于ELM的输入层与隐含层连接权值及隐含层偏置是随机选出的，这样做虽然可以使过程简化、计算速度更快，但也容易影响模型的稳定性及预测结果的准确性。通过增大隐含层节点数来提高预测精度，又会出现样本适应能力差、泛化能力下降等问题。因此，为了能够使模型具有更好的性能，需要在样本训练前，选择最优输入权值和隐含层偏置，确保ELM在最优隐含层节点时具备最佳预测效果。常用的参数寻优方法主要有启发式优化法和网格搜索法，后者主要的缺点是计算量大，计算成本高，因此，采用启发式优化法中的粒子群算法(particle swarm optimization，PSO)进行参数寻优[14-15]。粒子群算法(PSO)是一种基于群体的优化搜索方法，在ELM参数寻优中有着不错的应用效果。其具体流程如下。

步骤1初始化粒子群，在n维空间，粒子的位置矢量表示为xi=(x1,x2,…,xn)，粒子速度矢量表示为vi=(v1,v2,…,vn)。

步骤2评价粒子的适应度。

步骤3寻找局部最优解。

步骤4更新全局最优解。

步骤5通过迭代式(3)和式(4)，调整微粒速度和位置。

vi=ωvi+c1α(pi-xi)+c2β(gi-xi)

(3)

xi=xi+vi

(4)

式中：ω为惯性权值；c1和c2为学习因子，取常用值2；α和β为介于(0,1)的随机数；pi为个体最优位置；gi为全局最优位置。

惯性权值ω对寻优结果有着重要影响。若ω值偏大，则全局寻优能力强，局部寻优能力弱；偏小则全局寻优能力弱，局部寻优能力强。为了更好地平衡全局和局部搜索能力，选择动态ω，采用线性递减权值公式，即

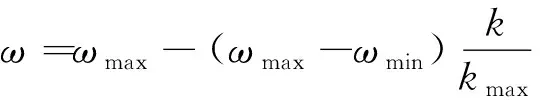
(5)

式(5)中：ωmax为权值最大值；ωmin为权值最小值；kmax为最大迭代次数。

步骤6达到结束条件则结束输出最优权值和偏置，否则转步骤2。

PSO-ELM模型算法流程图如图3所示。

图3 PSO-ELM算法流程图Fig.3 PSO-ELM algorithm flow chart

4 应用实例分析

4.1 建立产量预测模型

建立产量预测模式首先要选定好训练集和测试集。结合玛湖油田水平井自喷期产量主控因素分析，以油层厚度、地层压力、总砂量、渗透率、压裂簇数、含油饱和度作为输入，选取20口水平井，每口井各12个月的月生产资料，共计240个样本作为ELM学习样本组成训练集，再随机选取2口水平井共计24个样本作为测试集。其次，由于不同输入参数的量纲不同，从而使得数据间的数量级差距过大，从而影响模型的计算速度和准确性。因此在学习训练前，还需要对数据预处理。采用Z-Score标准化方法，将所有数据样本标准化，公式为

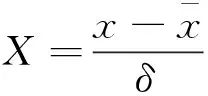
(6)

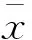
利用PSO寻找最优ELM输入权值与隐含层偏置，PSO参数设置为粒子群数M=50，粒子维数D=150，最大迭代数次数K=100，惯性权值ωmin=0.3，ωmax=0.7。最后，利用选定好的权值和偏置，进行ELM训练、预测。

ELM模型隐含层节点个数选择，直接影响预测结果准确性。优选最常用的Sigmoid函数[式(7)]作为激励函数，利用选好的样本进行测试，从而确定隐含层节点个数。隐含层节点个数初始值设为10，之后每次增加10，从而得到不同节点个数的预测正确率(图4)。

图4 不同隐含层个数预测正确率Fig.4 Correct prediction rate with different number of hidden layers

(7)

通过测试结果分析可知，预测结果的正确率随着隐含层节点个数的增加而提高，当节点个数大于100时，预测正确率趋于稳定，ELM模型隐含层节点个数取l=110。

4.2 模型应用分析

为了验证模型的性能，分别利用建立好的PSO-ELM水平井产量预测模型和单一ELM模型，对20口水平井组成的训练集进行预测，预测结果如图5所示，通过结果对比分析，发现PSO-ELM预测模型与常规ELM模型预测产量与实际数据的平均误差分别为0.53%和4.13%。

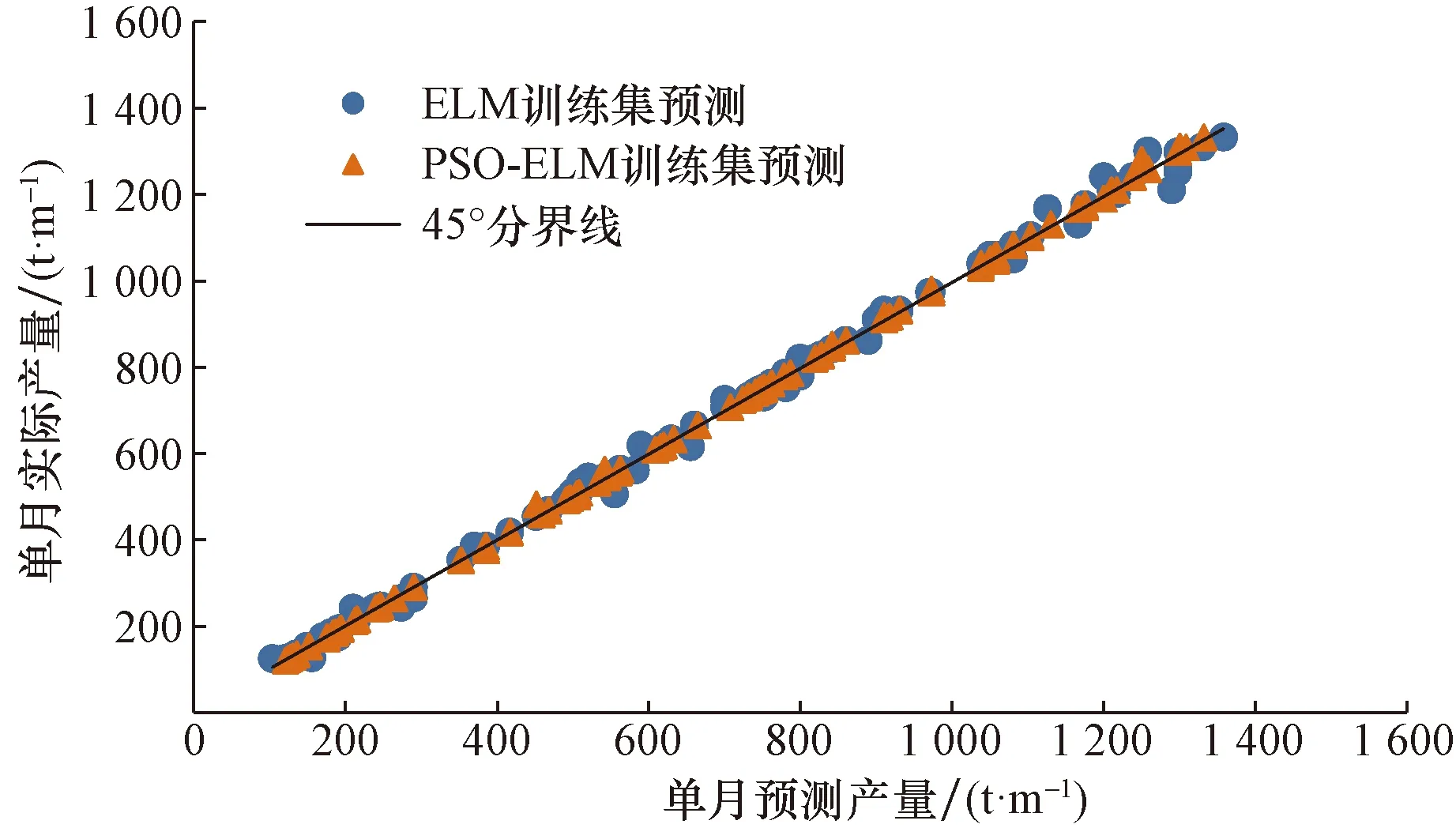
图5 训练集预测结果Fig.5 Prediction results of the training set

再分别利用单一ELM和PSO-ELM两种预测模型，对两口测试集水平井MaHW6105以及MaHW6106进行产量预测，预测结果如图6、图7所示，两种模型均能很好地反映研究区水平井“多段式”产量特征。通过数据分析对比，发现PSO-ELM模型预测效果明显优于单一ELM模型，预测产量与实际产量数据吻合度更高。其中水平井MaHW6105的PSO-ELM模型预测产量与实际产量平均相对误差为3.63%，相同模型下，水平井MaHW6106预测产量与实际产量平均相对误差仅为2.45%。

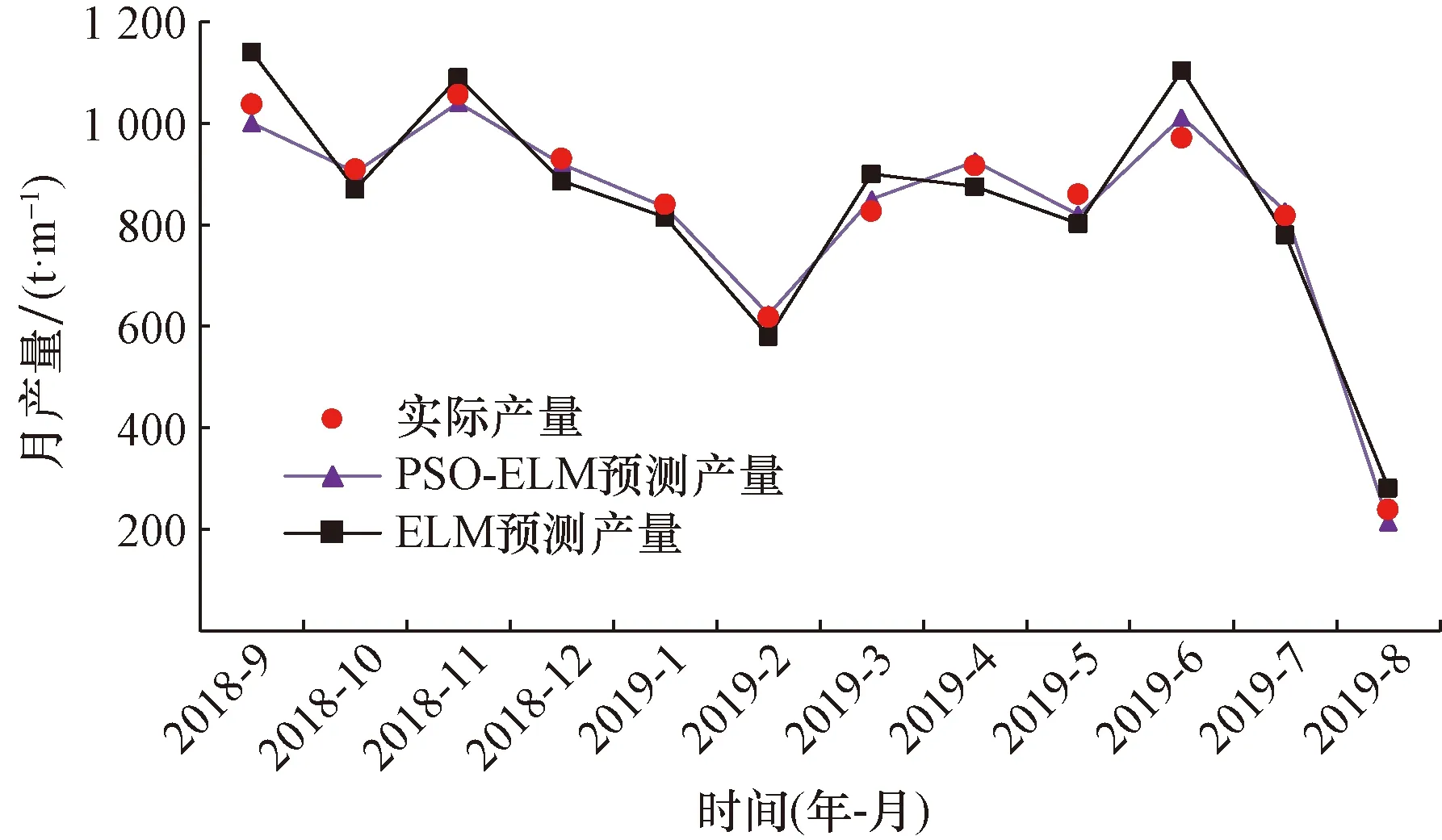
图6 MaHW6105水平井产量预测结果图Fig.6 MaHW6105 horizontal well production forecast results

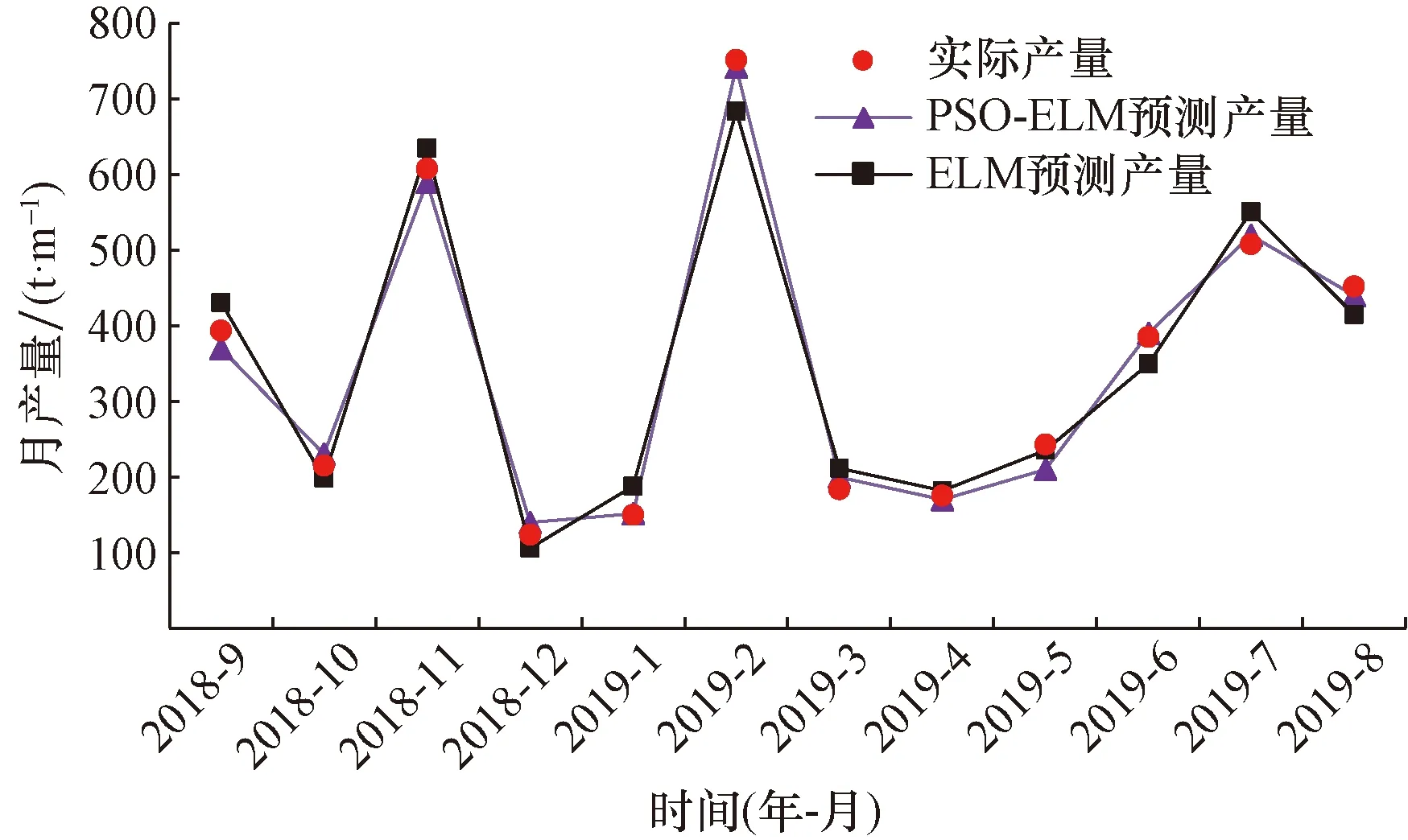
图7 MaHW6106水平井产量预测结果图Fig.7 MaHW6106 horizontal well production forecast results

为了更好地验证PSO-ELM产量预测模型的性能，在训练样本和测试样本外另选取5口水平井进行产量预测，预测结果见表3。预测产量与实际产量的平均相对误差在2.14%～5.28%，从而说明PSO-ELM模型在玛瑚油田水平井自喷期产量预测方面有着较好的应用效果。

表3 PSO-ELM模型预测结果Table 3 Results of PSO-ELM prediction

5 结论

(1)模型输入参数的选择，直接影响支持向量机产量预测模型的准确率。利用主成分分析法分析不同影响因素与产量间的相关性，确定了6类主控因素作为输入参数，从而提高了模型预测结果的准确性。

(2)粒子群算法在极限学习机参数寻优方面有着较好的应用效果。利用PSO选择ELM最优输入权值和隐含层偏置，建立水平井自喷期产量预测模型，预测结果与实际产量“多段式”特征吻合度高，效果显著。

(3)PSO-ELM产量预测模型，与传统的预测方法相比，具有计算速度快、泛化能力强、预测精度高等优点，在玛湖油田“多段式”特征水平井产量预测方面，有着良好的表现。