基于随钻测井数据预测破裂压力

郭大立，王玉基，张小栓，辛骅志，康芸玮

(1.西南石油大学理学院, 成都 610500; 2.新疆油田公司, 克拉玛依 834000)

破裂压力是压裂施工时的一项重要参数，能够较精确地预测出破裂压力值，对于安全施工具有重大意义。因准格尔盆地MH区块特殊的地质条件，该区块的油田开发效益遭受严重影响，施工现场在压裂过程中普遍存在油压过大、排量提升困难、施工压力高等严重问题，导致施工不能正常进行，酸化预处理是降低破裂压力的一种方式[1]，酸化预处理对岩石破裂压力的影响也有很多定量的计算方法[2-3]，主要是依据酸损伤变量预测任意时刻的破裂压力[4-5]。现有的方法大多仅依赖于应力分布和岩石性质等主要因素，缺乏对随钻测井数据的利用。通过对流体扫描成像(flow scanner image，FSI)产出剖面测井资料进行全面分析，建立数据驱动的机器学习模型，能够更好地适应不同区块的地质条件，发挥更加优良的效果。

目前国内外已经有很多关于破裂压力的数值模拟预测方法，如Hubbert-Willis(H-W)公式、Haimson-Fairhurst (H-F)公式、黄氏公式等。然而，随钻测井参数和实测破裂压力的回归预测模型却鲜有报道。数值模拟方法具有一定的缺陷，主要是一些参数求取困难且模型不能适用于任何地层。在开发过程中收集到一定的压裂数据资料时，应用数理统计的方法结合其已有的数据资料可以较准确地预测破裂压力，可以为后续开发提供基础信息并且节省开发成本，因此，FSI产出剖面测井技术在MH区块得到了应用，随钻测井资料是在施工时直接测量的，受外界影响较小，为预测破裂压力提供了一些数据资料，所以可以更真实地反映地层岩石特征。但单井一天的FSI测井花费近百万，极大地增加了该区块致密砾岩油藏的开发成本，将已经测出的157簇数据作为样本，利用统计数据建立破裂压力预测模型，进而降低压裂成本。

用统计模型预测破裂压力已经有相关文献。Ahmed等[6]采用5种方法(包括功能网络、人工神经网络、支持向量机、径向基函数和模糊逻辑)预测破裂压力并对比分析预测效果，结果表明人工神经网络预测精度最高；Yan等[7]分别将粒子群优化算法(particle swarm optimization，PSO)与反向传播(back propagation，BP)神经网络、极限学习机(extreme learning machine,ELM)和支持向量机(support vector machine，SVM)相结合预测破裂压力，并将它们预测结果与传统多元回归分析(multiple regression analysis，L-MRA)进行比较，预测精度按PSO-SVM、PSO-ELM、PSO-BPNN和L-MRA的递减顺序排列；李昌盛等[8]建立用遗传算法优化BP神经网络并将其应用于破裂压力预测，结果表明预测精度高于数值模拟方法。

准格尔盆地MH区块的致密油储层具有低孔和低渗的特点，H-W模型是目前使用最多的模型，但H-W模型预测精度较低，效果较差。非线性映射能力强和学习速度快是广义回归神经网络(generalized regression neural network，GRNN)模型的两大优点，最终网络收敛到样本量积聚较多的优化回归面，它对样本较少时的预测效果比其他神经网络模型更优，对于不稳定的样本数据也能较好地处理[9]，十分契合所选用的数据特点，与其他模型相比，GRNN模型方便设置参数，操作简便，只需要调整一个光滑因子就可以调整网络的性能，对石油工程而言，其具有重要的实用性，所以尝试利用GRNN建立模型预测破裂压力。

为降低MH区块的开发成本和施工危险，现基于MH区块FSI测井资料，首次提出将GRNN模型应用于该区块的破裂压力预测，并对比分析及进行现场实验，证明该预测模型的有效性，以期为该区块的油井开发节约成本，并降低施工风险。

1 MH区块概况

1.1 地质概况

MH区块位于准格尔盆地玛湖凹陷中部，探矿面积7 300 km2。该地区地质独特，主要特点是埋藏深、物性差、非均质性强、岩石塑性，砾石粒径变化大、天然裂缝不发育等[10-11]，主要是靠压裂形成的人工裂缝实现石油增产[12-13]。岩性以中砾岩为主，其次为小砾岩和细砾岩。

1.2 资源分布概况

准格尔盆地MH区块是世界上迄今规模最大的砾岩油田，石油资源丰富，石油资源量156亿t，目前已探明的石油储量为68亿t[14]，如图1所示。

图1 MH区块资源分布图Fig.1 Resource distribution map of MH block

2 模型建立

2.1 数据来源

针对MH区块所有致密油井，利用FSI产出剖面测井资料和压裂施工秒点数据共匹配出157簇样本，其中经过酸预处理后的样本有51簇，未泡酸的样本有106簇。MH区块所有井的酸化预处理工序均一致，采用15%盐酸，酸液用量固定为5 m3，现场泡酸时间均为30～60 min。

2.2 破裂压力的计算

根据现场压裂施工秒点数据可以得到每一级首个发生起裂的簇在起裂瞬间(破裂点)的施工压力、排量和井底压力，此时的井底压力就是首个起裂簇的缝口压力，而在岩石起裂的瞬间缝口压力就等于该簇的破裂压力。任意时刻任意一簇的缝口压力计算公式为

pf=ps+py-Δpt-Δpm

(1)

式(1)中：ps为井口压力，MPa；py为液柱压力，MPa；Δpt为孔眼摩阻，MPa；Δpm为垂直段和水平段的沿程摩阻，MPa。

孔眼摩阻和沿程摩阻的计算公式如下。

(1) 孔眼摩阻[15]计算公式。

(2)

式(2)中：qi为裂缝入口处的流量，m3/min；ρ为压裂液的密度，kg/m3；np为该簇的射孔数量；dp为射孔孔眼的直径，m；Kd为流量系数，孔眼完好时Kd∈[0.5,0.6]，孔眼被完全磨蚀时Kd=0.95。

(2) 沿程摩阻[16]计算公式。

(3)

式(3)中：σ为降阻比；Δp0为清水摩阻，MPa；Q为流体排量，m3/min；D为管柱内径，mm；L为管长，m；CHPG为稠化剂的浓度，kg/m3；Cp为支撑剂的浓度，kg/m3；当Cp=0(即不加支撑剂)，化简式(3)就可得出前置液阶段的降阻比计算公式。

2.3 参数选取

影响破裂压力的因素众多，主要与地层条件、施工条件、裂缝产生方式、油气井完井方式有关。分析对比已有的破裂压力预测模型发现其主要与埋深(DEP)、岩石密度(DEN)、泊松比(μ)、自然伽马(GR)、弹性模量(E)、声波时差(AC)、补偿中子(CNL)、地层电阻率(RT)这8个参数(如表1所示)有关，由埋深、岩石密度和声波时差可以得出上覆地层压力与孔隙压力[17]；泊松比主要反映岩石的塑性，泊松比越大表明破裂压力越大；自然伽马主要可以用来划分岩性；弹性模量可以用来衡量岩石的刚度，其值越大表明破裂压力也越大；补偿中子可以反映出孔隙度大小；随着埋深增加，电阻率减小，则孔隙度也相应地减小。

表1 参数详情Table 1 Parameters for details

2.4 破裂压力预测GRNN模型

1991年，美国学者Donald F.Specht首次设计并提出了GRNN模型其结合数理统计知识，可根据样本数据中的隐含关系不断地逼近真实值，它是一种基于径向基函数(radical basis function，RBF)改进之后的神经网络模型，GRNN和RBF的主要区别是在RBF的隐含层与输入层之间将原来的RBF模型中的权值连接替换成了求和层，训练集的转置是连接隐含层与求和层间的权值。GRNN网络结构[18-19]如图2所示。

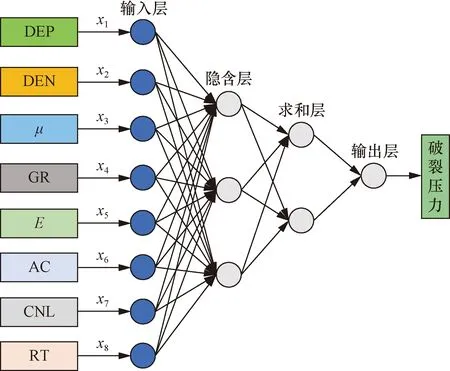
x1～x8表示8个变量图2 GRNN模型结构图Fig.2 GRNN model structure diagram

(1) 输入层。对应网络的输入为X=[DEP,DEN,μ,GR,E,AC,CNL,RT]，神经元个数和输入向量维数相同，先将所有输入数据标准化处理后再代入模型之中，然后传递到隐含层。

(2) 隐含层。隐含层神经元的数量由训练样本的数量决定，样本数据在这一层进行核函数运算后再传递到求和层[20]，其中传递函数为

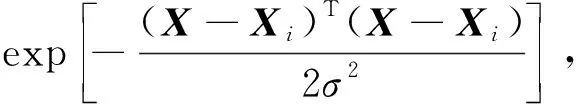
i=1,2,…,n

(4)

式(4)中：X为输入向量；Xi为第i个学习样本；σ为光滑因子。给出X，则变量X与学习样本Xi之间的Euclid距离的平方就作为神经元Pi的输出值，则为

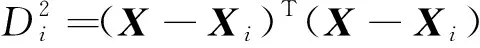
(5)

(3) 求和层。该层节点个数为输出层节点个数加1,求和层共有两个输出节点，其中一个节点的输出为隐含层输出结果的算术和，计算公式为

(6)

另一个节点的输出为隐含层的输出结果进行加权之后的和，计算公式为

(7)

(4) 输出层。该层的节点数与训练样本的输出变量个数相同，其计算方式是用上一层的输出比上上一层第一节点输出结果，该层节点个数为1，即破裂压力，计算公式为

实现方式：在施工开始前或深化设计过程中利用BIM技术的可视化及可协调特性对各个专业（建筑、结构、给排水、机电、消防等）的设计进行空间协调，检查各个专业管道之间的碰撞以及管道与结构的碰撞，避免施工中管道发生碰撞和拆除重新安装的问题（见图15、图16）。

yi=SD/SNj,j=1,2,…,k

(8)

反复调整网络参数以获取最优的网络结构。网络训练的方式是交叉验证，主要优化参数是σ，σ表示GRNN的光滑因子。适应度函数表达式为

fitness=argmin(MSEpredict)

(9)

用训练后的均方误差(mean squared error，MSE)作为适应度函数。MSE误差越小，说明预测数据与原始数据的吻合度就越高。最终优化的输出未泡酸样本为0.2，泡酸样本为0.1。

GRNN预测破裂压力技术路线如图3所示。

图3 技术路线图Fig.3 Technology roadmap

2.5 模型评价

选取均方根误差(root mean squared error，RMSE)与平均百分比误差(mean absolute percentage error，MAPE)两项评价预测模型误差，计算公式如下。

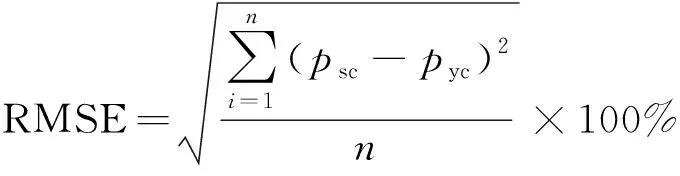
(10)

(11)

式中：psc为破裂压力实测值，MPa；pyc为破裂压力预测值，MPa；n为样本数量。

3 实例分析

为了验证GRNN预测破裂压力的可行性，现场组织实施了测验活动，以MH区块MH-1井为例，施工井段4 120～4 900 m，水平段长度1 858 m，压裂20级33簇，分为泡酸和未泡酸样本，泡酸样本为10簇，未泡酸样本有23簇。将上述8个参数作为输入，破裂压力作为输出值，并将该井预测结果与BP神经网络预测结果及H-W模型预测结果以可视化方式展现出来，可以更直观地突出GRNN模型相比于其他破裂压力预测模型的优势。

表2给出了MH区块MH-1井部分测井数据，表2中的1～23序号数据为未泡酸样本，24～33序号数据为泡酸样本。

表2 MH区块MH-1井部分测井数据Table 2 Partial log data from well MH-1 in Block MH

从单井各级的施工曲线可以得到每一级第一个发生起裂的簇在起裂瞬间(破裂点)的施工压力、排量和井底压力，此时的井底压力等于第一个起裂簇的破裂压力。计算井底压力的过程中，需要根据秒点数据时刻考虑排量、砂浓度和井口压力的变化，这样得到的缝口压力才具有可靠性。各个簇在起裂的瞬间，压裂液仅在管柱中压缩形成憋压状态，孔眼处无压裂液经过，故此时的孔眼摩阻为0。一旦某一簇被压开，井筒中的压裂液会以该簇的射孔为突破口挤入缝内，不会经过该簇之后的所有簇，故该簇之后的沿程摩阻为0。

应用FSI流动扫描技术可以得到不同井各级的产出剖面测井解释结果，如图4所示。从解释结果可以确定不同簇的射孔位置处是否有产出(产油、产水和产气)，故可以确定该簇是否被压开，从而可以明确任意一段具体是哪几簇已经起裂。

根据压裂施工秒点数据可以得到不同井各级的施工曲线。如图5所示，施工曲线上井底压力的首个峰值即是最小主应力最小的簇的破裂压力。砂堵后(第一次加砂完毕后)继续压裂，施工曲线上的井底压力会出现第二个峰值，若该值大于第一个峰值则表明砂堵成功，施工曲线出现两次峰对应的FSI产液剖面测井资料也应该对应出现两个射孔有液体产出，这样才能确定是有新的簇被压开，意味着最后发生起裂的簇是破裂压力更大的新簇，也是所有起裂的簇中破裂压力最大的簇，其对应的最小主应力在所有起裂的簇中也最大。若第二个峰值小于第一个峰值则表明砂堵失败，意味着没有新簇发生起裂，只是在砂堵前就已经起裂了的老簇再次被打通，故此种情况下的第二个峰值便无参考意义。

图5 MH区块MH-1井第20级施工曲线Fig.5 Construction curve of class 20 of well MH-1 in MH Block

根据测井数据可以计算得到破裂点的井底压力(即起裂簇的破裂压力，如图5所示)，利用FSI产出剖面测井资料可以准确得出单井每段具体是哪几簇起裂(如图4所示)。各簇按照破裂压力由低到高的顺序(也是最小主应力由低到高的顺序)依次起裂，故综合两个结果就可以将破裂压力与起裂的簇进行匹配，从而确定首次和末次发生起裂的两个簇的破裂压力真实值，中间发生起裂的簇其破裂压力无法进行匹配。

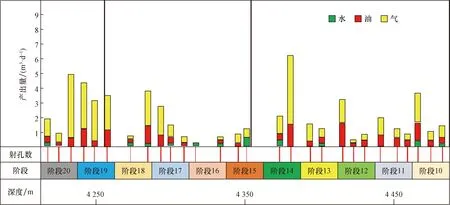
图4 FSI生产剖面测井解释结果图Fig.4 FSI production profile log interpretation result diagram

3.1 不同模型对比

为讨论酸预处理对岩石破裂压力的影响，对泡酸样本和未泡酸的样本分开建立GRNN模型，并与BP神经网络模型和H-W模型预测的结果进行比较，H-W模型的计算方式为

pb=3σh-σH+σf-po

(12)

式(12)中：pb为破裂压力，MPa；σh为最小主应力，MPa；σH为最大主应力，MPa；σf为岩石抗张强度；po为孔隙压力，MPa。

3种预测模型预测结果与实测破裂压力值的对比分析结果如图6所示。

图6是对泡酸样本和未泡酸样本分开建立3种模型，对比分析预测效果，可以直观看出，无论是泡酸样本还是未泡酸样本，3个模型中GRNN模型预测效果都是最佳。由于无法对泡酸后的岩石样本进行现场取样，所以没有进行电镜扫描实验，故无法确定酸处理后岩石弹性模量和脆性指数等参数的取值，因此不能利用H-W公式计算泡酸后的岩石破裂压力。故仅对未泡酸的样本进行破裂压力H-W模型计算。根据建立的模型分别对泡酸和未泡酸样本进行预测精度对比分析，结果如表3所示。

图6 未泡酸样本和泡酸样本的预测结果与实测值对比图Fig.6 Comparison of predicted results and measured values of unfoamed acid and foamed acid samples

由表3可知，GRNN模型的预测误差在3个模型中是最小的，而且无论是未泡酸样本还是泡酸样本，GRNN模型的预测误差浮动较小，所以,GRNN模型可以更好地预测MH区块的破裂压力值。

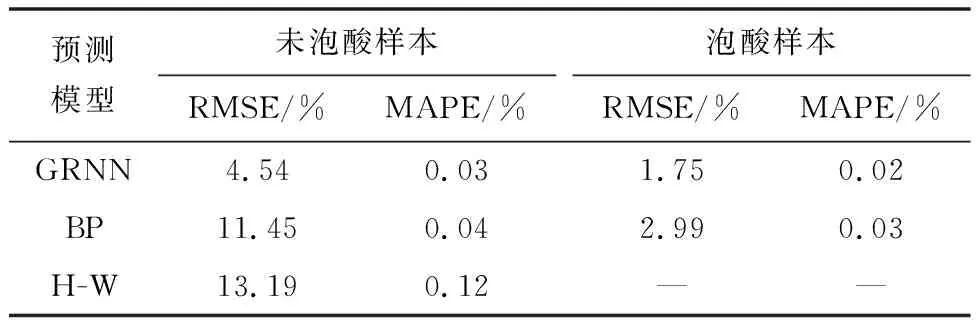
表3 3个模型预测误差对比Table 3 Comparison of prediction errors of the three models

3.2 泡酸分析

针对MH区块的所有致密油井，按现场的区块划分为A、B、C三大区块并分别统计了泡酸和未泡酸井的平均破裂压力，并从数据的角度出发，根据统计结果给出了不同区块的酸化预处理建议，具体结果如表4所示。

从表4可以看出，A区块的井泡酸与否结果并无明显差异，根据统计结果可建议A区块的井压裂施工不进行酸化预处理，这样能够在保证同等压裂效果的同时降低一定成本。B、C区块经过泡酸之后，破裂时的排量明显较大，这表明酸化预处理能够为大排量施工提供保障，而且能降低压裂过程中的风险。

表4 MH区块井分区块统计结果Table 4 Statistical results of well blocks in MH block

同时，经过酸化预处理之后，B、C区块的破裂压力显著下降，为压裂过程中井底憋压提供了更大空间，降低了施工风险，因此建议B、C区块其余井同样进行酸化预处理。

3.3 应用于不同区块对比分析

在研究了MH区块后，对AH区块136条数据进行预测并与MH区块进行对比分析。将AH区块的8个主控因素作为输入，利用GRNN 模型进行预测，预测误差分析如表5所示。

由表5可以得出，GRNN模型预测AH区块破裂压力效果较好，与MH区块的预测误差对比浮动较小，所以GRNN模型预测破裂压力具有普适性。

表5 AH与MH区块对比分析Table 5 Comparative analysis of AH and MH block

4 结论

由于MH区块的酸化预处理工序固定且单一，因此仅从统计角度进行定性分析给出不同区块的酸化预处理建议。针对不同的酸液类型以及酸液浓度、酸液用量和酸化时间进行大量的实验从而给出最优的酸化预处理方案仍是值得研究的问题。通过综合分析得出以下结论。

(1) 综合利用FSI产出剖面测井资料和现场压裂施工秒点数据确定了单井各段不同簇的破裂压力真实值。

(2) 综合利用FSI产出剖面测井数据资料和地质参数建立预测岩石破裂压力的GRNN模型。GRNN模型考虑了埋深、泊松比、弹性模量、岩石密度、自然伽马、声波时差、补偿中子、地层电阻率这8个主要影响因素，通过现场实验验证，结果证明，该模型相比于BP神经网络和H-W模型具有更好的普适性及可靠性。

(3) 酸化预处理可以起到降低储层破裂压力作用，为压裂过程中的井底憋压提供更大的空间，合理地对油井进行酸化预处理不仅可以降低施工风险，保证压裂施工的有效性，而且可以为油井开发节省成本。