矩形平板的声辐射效率计算

钟 策，陈 赫

（上海索辰信息科技股份有限公司，上海 201204）

振动结构的声辐射效率是其声辐射性能的一个重要表征参量，反映了振动结构向周围介质中辐射声能量的能力，是工程技术人员在进行声学结构设计时需要考虑的重要参数。其中平板的辐射效率计算是统计能量分析方法的基础问题，可用于平板与声腔耦合结构的声振问题求解。

Xie 等[1]使用瑞利积分求得球坐标系下远场任意一点的声强，再将声强对球面进行积分，得到了矩形简支板各阶模态辐射效率的解析表达式。梁健等[2]推导了带刚性障板的平板各阶弯曲振动模态的声辐射效率幂级数表达式，计算了不同边界条件下平板的声辐射效率。任惠娟等[3]通过声强对辐射面积分，得到了四边简支矩形板的模态辐射声功率的精确解析表达式，并采用了十节点的高斯-勒让得求积法进行数值计算，计算精度较高。张凯等[4]基于Mindlin 厚板理论建立了四边简支矩形平板的振动声辐射数学计算模型，通过Rayleigh 积分法得到模态声辐射系数，并得到结论：由于Mindlin 厚板模型考虑了板的横向剪切变形和转动惯量，其动力学计算结果比经典薄板理论更精确，但由于声辐射仅与平板的横向振动相关，因此2 种模型计算出来的平均辐射效率没有明显区别。

1 辐射效率积分

假设一个面积为S（00 的半无限大空间。基于Rayleigh 积分，板对空间的时域平均辐射功率为

对于简支板，板的模态振型可表示为

式中：kx=mπ/a，ky=nπ/b 分别表示x 和y 2 个方向的波数分量。

对波数进行无量纲化

板的辐射效率σ 可表示为

进行变换

射效率σ 可表示为

可将积分式化为

积分区间：C（10<θ<θ0），θ0），C4（π-θ0<θ<π），C5（π<θ<π+θ0），C6（π+θ0<θ<3π/2），C7（3π/2<θ<2π-θ0），C8（2π-θ0<θ<2π），其中θ0=arctan（b/a），积分函数如下

注意到积分函数Gn是连续函数，其中l（θ）=1-αcos θ-βsin θ。

2 奇点近似处理

在计算积分时需要把l（θ）=0 的奇点排除，如图1所示，2 个切点即为奇点，给定任意点（α，β）可以画出单位圆的2 条切线，对应2 个零点θ1、θ2。图1 中给出了对一个特定的（α，β）对应的2 个零点θ1、θ2的几何结构。2 个零点的位置在图2 中表示，若（α，β）在Z28区域，则其中一个零点在C2范围内，另外一个零点在C8范围内。当（α，β）穿过边界线Lij，一个零点从Cn穿越到另一个范围。

图1 l（θ）的零点几何结构图

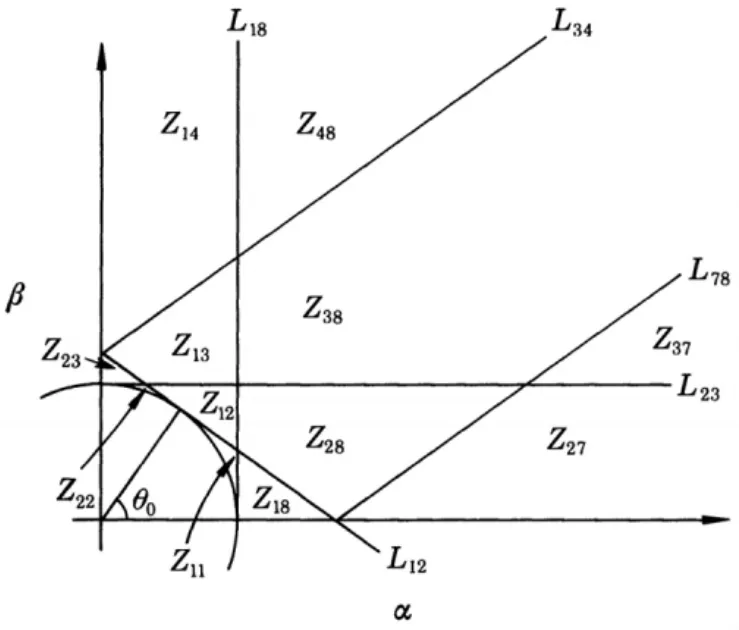
图2 波数图（Zij 表示奇点位于Ci 和Cj）

由式（9）—式（12）可知，积分项主要贡献来自于奇点附近，将积分公式化为分段积分，并在奇点附近进行简化可得出近似公式[5]。近似公式分为3 种情况：①α2+β2<1-∊；②α2+β2≈1；③α2+β2>1+∊。不同α 和β 的取值分别计算出对应的σ，平均辐射效率σ¯需要对所有可能的模态进行平均

式中：α=μcosφ，β=μsinφ，小量∊的定义为∊=π（k2ab）-0.5。

在不考虑Transition region（上图中各边界线附近区域）的情况下，有如下几种形式

3 过渡区

3.1 过渡线L18

假设（α，β）靠近L18（α+1），但是不太靠近β=0，在这种情况下将会存在2 个分开的奇点，其中一个奇点θ*靠近θ=0，此奇点会对σ 产生附加项

式中：sgn（1-α）为±1，符号由1-α 的符号确定，Si（x）=dt。

3.2 过渡线L23

L23与L18同理，可以得到附加项

其余过渡线对辐射效率产生的附加项为0。

4 数值算例

4.1 半无限声场辐射

以1 m×1 m×0.005 m 的方形铝板为例计算辐射效率，材料参数：杨氏模量E=7.0×1010Pa，密度ρ=2700kg/m3，泊松比μ=0.33。计算结果与成熟商业软件VAONE 计算结果进行对比，图3 为辐射效率对比曲线，图4 为辐射效率偏差曲线。

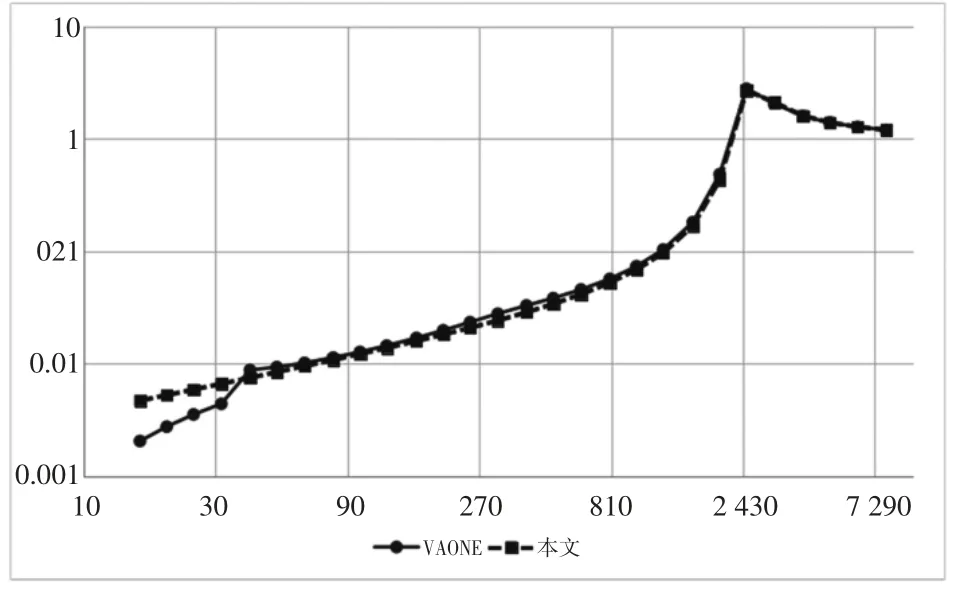
图3 辐射效率对比曲线

由图3 和图4 可知，平板辐射效率计算结果在主要频率范围内均与VAONE 吻合较好，考虑过渡区与不考虑过渡区计算结果区别较小，当固定过渡区小量时，在高频时计算结果出现较大偏差，是由于频率增加，小量∊=π（k2ab）-0.5也增加，固定的小量不满足计算精度要求。

图4 辐射效率偏差曲线

添加一个半无限场，半无限场与平板耦合连接，声学介质为空气，密度ρ=1.225 kg/m3，声速c=343 m/s。计算平板辐射声压；载荷采用1 N 点力，计算频率为1/3倍频程100～8000 Hz，统计能量模型如图5 所示。得到半无限声场的声压曲线，如图6 所示。

图5 平板与半无限场耦合统计能量模型

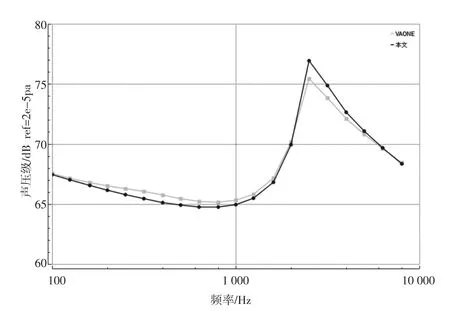
图6 半无限场声压曲线

4.2 平板与声腔耦合

以平板与声腔耦合为例，平板结构为1 m×1 m×0.005 m 的方形铝板，材料参数：杨氏模量E=7.0×1010Pa，密度ρ=2700 kg/m3，泊松比μ=0.33，声腔几何尺寸为1 m×1 m×1 m，声学介质为空气。建立统计能量模型，子系统包括一个平板结构子系统和一个声腔子系统，平板与声腔直接建立一个面连接，统计能量模型如图7 所示。将本文计算结果与成熟商业软件VAONE 计算结果进行对比，平板结构的平均速度曲线如图8 所示，声腔的声压级1/3 倍频程曲线如图9所示。

图7 平板与声腔耦合统计能量模型

图8 平板平均速度曲线

由图8 和图9 可知，平板速度结果与VAONE 软件结果基本一致，同时采用本文方法计算得到的声腔声压级结果与VAONE 计算结果基本吻合，表明本文方法平板声辐射效率与成熟振动噪声商业软件VAONE 结果一致，验证了结果的准确性。

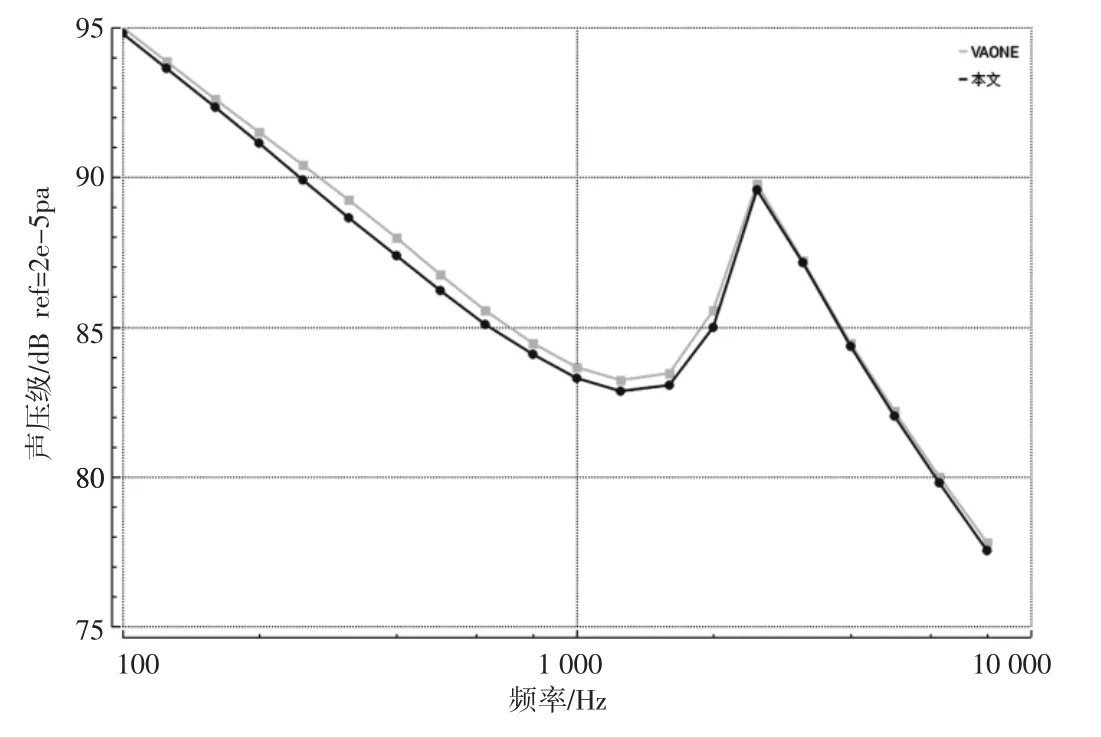
图9 声腔声压级曲线

5 结论

本文基于Rayleigh 积分推导了四边简支平板结构的声辐射效率积分表达式，对奇异点处进行了近似处理。最后计算了1 m×1 m×0.005 m 矩形铝板结构与半无限场和声腔耦合下的声辐射效率，振动噪声计算结果与振动噪声领域成熟商业软件VAONE 进行对比，计算结果吻合较好，验证了本文方法可应用于统计能量分析中平板的声辐射效率计算。