Influence and Correction of Wavefront Primary Aberrations for Radio Telescopes using Aberration Theory

Bin-bin Xiang ,Wei Wang ,You Ban ,Shang-min Lin ,Zhi-gang Wen ,Da-lin He ,and Ming-hui Cai

1 School of Mechanical Engineering,Xinjiang University,Urumqi 830017,China;xiangbinbin031@163.com

2 School of Mechano-Electronic Engineering,Xidian University,Xi’an 710071,China

3 Xi’an Institute of Optics and Precision Mechanics,Chinese Academy of Sciences,Xi’an 710119,China

4 Xinjiang Astronomical Observatory,Chinese Academy of Sciences,Urumqi 830011,China

Abstract Dual-reflector antennas are widely used in astronomical observations and satellite communication.Structural deformations of the reflectors for radio telescopes are inevitable in outside working conditions due to exterior environment loads,which will cause distortion in the surface of the primary reflector and displacement of the subreflector,then lead to gain degradation and misalignment.In this paper,the influence and correction of misalignment in a dual-reflector antenna have been studied.From the perspective of wavefront aberration,a method is proposed to correct the wavefront primary aberration by adjusting the subreflector position.The characteristics of wavefront errors caused by structural deformation of the reflector have been analyzed,and relationships between the position motions of the subreflector and the Seidel wavefront aberrations are derived.The adjustment quantities of the subreflector are also derived.The results show the appropriate positional change of the subreflector in the lateral and axial directions can effectively correct the effects of the tilt and defocus in the primary aberrations caused by antenna structural deformations.

Key words: telescopes–methods: analytical–instrumentation: miscellaneous

1.Introduction

Because of the high gain and low sidelobes,dual-reflector antennas are widely used in astronomical observation,satellite communication,radar,and so on.Because of usual outside working conditions,the structural deformations of dual-reflector antennas,typical for radio telescopes,are usually inevitably caused by environmental loads,such as gravity,thermal effects,and wind (Imbriale 2001;Duan &Wang 2009;Li et al.2012).These environmental loads would induce antenna structural deformation,typical for the reflector surface distortion and subreflector displacement.Moreover,the fabrication of antenna parts would cause reflector surface distortion.It is well known that the distortion of the reflector surfaces will cause degradation in antenna electromagnetic performance (EMP),such as gain loss,sidelobe increase,and beam pointing deviation.Moreover,the effect of structural deformation on the EMP will vary with the variation of working conditions.The gain loss induced by the surface distortion may be calculated approximately by the root mean square (rms) error of the reflector according to the Ruze formula(Ruze 1966).Whereas,there is no expression to estimate approximately the influence of the misalignment of the dualreflector antenna on the EMP.

In order to reduce the effects of structural deformations,deviation compensation is generally necessary to improve antenna EMP.The adjustment of subreflector position is a low cost and effective means to compensate path length difference(PLD)caused by the surface distortion,misalignment,and beam boresight pointing deviation (Wang et al.2018).In optical telescopes and radio antennas,such an approach has been an important correction technique for misalignment and wavefront error,and it has been studied and used extensively (Thompson et al.2009;Schmid et al.2010;Wang et al.2014a;Duan 2016;Ju et al.2016;Xu et al.2016).

In optical telescopes,wavefront aberration can be measured directly with a dedicated wavefront sensor.With the measured aberration,misalignments can be solved by aberration modes decomposition,which relies on the relationship between aberration and movements of the secondary mirror(Schmid et al.2010).This method has been widely implemented in optical telescope engineering,such as the three-mirror anastigmat(Thompson et al.2009),the New Solar Telescope (Ju et al.2016),etc.

The reflector positional deviation of the dual-reflector antenna,which is a typical misalignment,can cause EMP degradation.The influence of misalignment can be separated into two components,one is induced by the subreflector translation,the other is induced by the subreflector rotation,then the beam deviation and gain loss can be computed separately(Zarghamee&Antebi 1985;Kim et al.1996);such a process operates in the Tianma 65m(TM65m)telescope,which obtains the optimal position of the subreflector by moving the subreflector and measuring intensity change (Wang et al.2014a).The subreflector’s positional adjustment can be determined by the best fitting paraboloid method (Wang et al.2014b;Yuan 2022).The best fitting is accomplished by adjusting the subreflector position to match the best fitting paraboloid,then which can be used to get the fitted position of the primary focus or subreflector.The position of the subreflector can be determined to maximize the antenna gain(Doyle 2009;Ban et al.2018;Xiang et al.2018).The best fitting paraboloid is an optimal geometric matching method,and the maximizing gain method is an optimal EMP method.Furthermore,the adjustment value of the subreflector for all elevation angles can be obtained by an interpolation calculation of the deformed surface data (Duan 2016).It seems to us that these methods can obtain the optimal position of the subreflector,but these cannot make everyone understand the characteristic of wavefront errors with and without adjustment.

It is well known that geometrical optics can compute the PLD or wavefront errors induced by the reflector deformations according to the deformed reflector surface.Furthermore,the wavefront phase of an antenna may be measured indirectly by a microwave holography technique in practice,which utilizes the Fourier transform relation between the complex far-field radiation pattern of the antenna and the complex aperture distribution to reconstruct the wavefront phase from the far-field radiation pattern (Rochblatt &Seidel 1992;Wang et al.2017),and it can provide a basis for the wavefront feature analysis.We think that the analysis of the influence of misalignment from electromagnetics and optics may be of great value.Therefore,in the present work geometrical aberration theory is used to study the influence of misalignment,and a method of subreflector positional adjustment is proposed.In this paper,the effects on wavefront aberrations induced by structural deformation are analyzed based on the Seidel aberration.The formulas of the Seidel aberration induced by the subreflector misalignment are derived.Based on the idea of minimizing the primary aberration,the determination method of subreflector adjustment position is proposed.The results,obtained for a 25 m Cassegrain antenna,indicate a suitable translation of the subreflector in the focal length and lateral directions can effectively correct the effects of tilt and defocus in the primary aberrations caused by antenna structural deformations.

2.The Wavefront Error of the Aperture Field Induced by Structure Deformation of Dual-reflector Antennas

In this paper,we only consider the phase errors due to subreflector displacements induced by antenna structural deformation.Based on the principle of geometrical optics,the total PLD in the aperture plane for a dual-reflector antenna is mainly the sum of the PLD due to the surface distortion of the primary reflector and the subreflector displacements and can be expressed as

where (r′,θ′) is the polar coordinate of a point in the aperture plane,δ0is the total PLD,δpis the PLD due to surface distortion of the primary reflector,and δsis the PLD due to subreflector displacements.Because the PLD of each location in the aperture plane is different,it results in the phase difference of different positions in the whole aperture plane,or in other words the phase errors in the whole aperture plane.The relationship between phase errors and PLD can be expressed as

wherek=2π/λ,and λ is the antenna working wavelength.The configuration of the Cassegrain antenna is illustrated in Figure 1.

Figure 2.The effect of subreflector displacement on the Seidel aberration coefficient.

Figure 3.Schematic of the effect of subreflector displacement of the Cassegrain antenna on the wavefront aberration.

Figure 4.The geometry of the 25 m Cassegrain antenna.

Figure 5.Wavefront errors associated with the gravity deformations of the reflectors at 10°,45°,and 80°,from left to right respectively.

Figure 6.Residual wavefront errors with the subreflector position adjustment at 10°,45°,and 80°,from left to right respectively.

The PLD caused by the surface distortion of the primary reflector is equal to twice the product of the displacement vector and the normal vector at the distortion point(Zarghamee 1982).Let {Up}=[Δxp,Δyp,Δzp]Tbe a displacement vector at a point on the primary reflector,then the PLD induced by the surface deviation is given by

where {Cp}=(c osα,cosβ,cosγ)is a unit normal vector at{Us}=[Δxs,Δys,Δzs]Tis the translation vector and that point.

Suppose the deformation of the antenna structure will cause rigid-body displacements of the subreflector,where{φs}=[Δφx,Δφy]Tis the rotation vector.The PLD caused by subreflector displacements of the Cassegrain antenna are shown in Table 1,and total PLD can be expressed as(Ruze 1969)

Table 1 Form of PLD for Subreflector Displacement (Ruze 1969)

3.Influence of the Subreflector Misalignment on Geometrical Aberration

It is well known that subreflector displacement will cause misalignment,PLD,and geometrical aberration.From the distribution of the wavefront errors,the misalignment causes global wavefront variation,which has the characteristics of primary geometrical aberration according to Seidel aberration theory,typical for piston,tilt,defocus,astigmatism,and spherical aberration (Wyant &Creath 1992;Xiang et al.2019a,2019b).

Let us rewrite Equation (4) in polar coordinates,and combine like terms,then the different primary aberrations can be obtained (Xiang et al.2019b).The PLD caused by the subreflector axial translation Δzscan be expressed as

The PLD caused by subreflector lateral translation Δrsat anglecan be expressed as

The PLD caused by the subreflector rotation/tilt Δαsat anglecan be expressed as

According to Seidel aberration,it is known to us from Equations (5)–(7) that the subreflector axial translation will cause the primary aberrations of spherical,defocus,and piston;the subreflector lateral translation will cause tilt and coma;the tilt of subreflector will cause tilt and coma.We also find that the primary aberrations induced by the subreflector lateral translation and tilt are almost the same as those induced by tilt and coma.

The effect of the subreflector displacement on the Seidel aberration coefficient is shown in Figure 2.As can be observed,under the case of the same small displacement range,the subreflector axial translation will mainly induce the aberration characteristic of the defocus,while the subreflector lateral translation and tilt will mainly induce the aberration characteristic of tilt.According to Equations (5)–(7),the total PLD caused by the subreflector displacements can be expressed as

It can be found that the aberrations caused by the subreflector displacements are mainly the low order errors and the large scale space errors.According to the Seidel aberration,Equation (8) can be rearranged as:

It is seen from Equation (9) that the subreflector lateral displacement will induce the tilt and coma,the subreflector axial displacement will induce the piston,defocus and spherical aberration,and the effect of subreflector rotation/tilt is the same as lateral displacement.Moreover,the relations between subreflector displacements and aberration coefficients are linear.The schematic of the effect of subreflector displacement in a Cassegrain antenna is drawn in Figure 3.As is apparent in Equation (9) and Figure 3,considering that the lateral translation and rotation of the subreflector almost have the same effect on aberration,we mainly consider the effect and correction of the axial and lateral translation in the following parts.

Figure 7.Radiation patterns computed with and without the subreflector position adjustment at 10°,45°,and 80°.

Figure 8.Primary aberrations with adjustment of the position of the subreflector with various elevation angles.

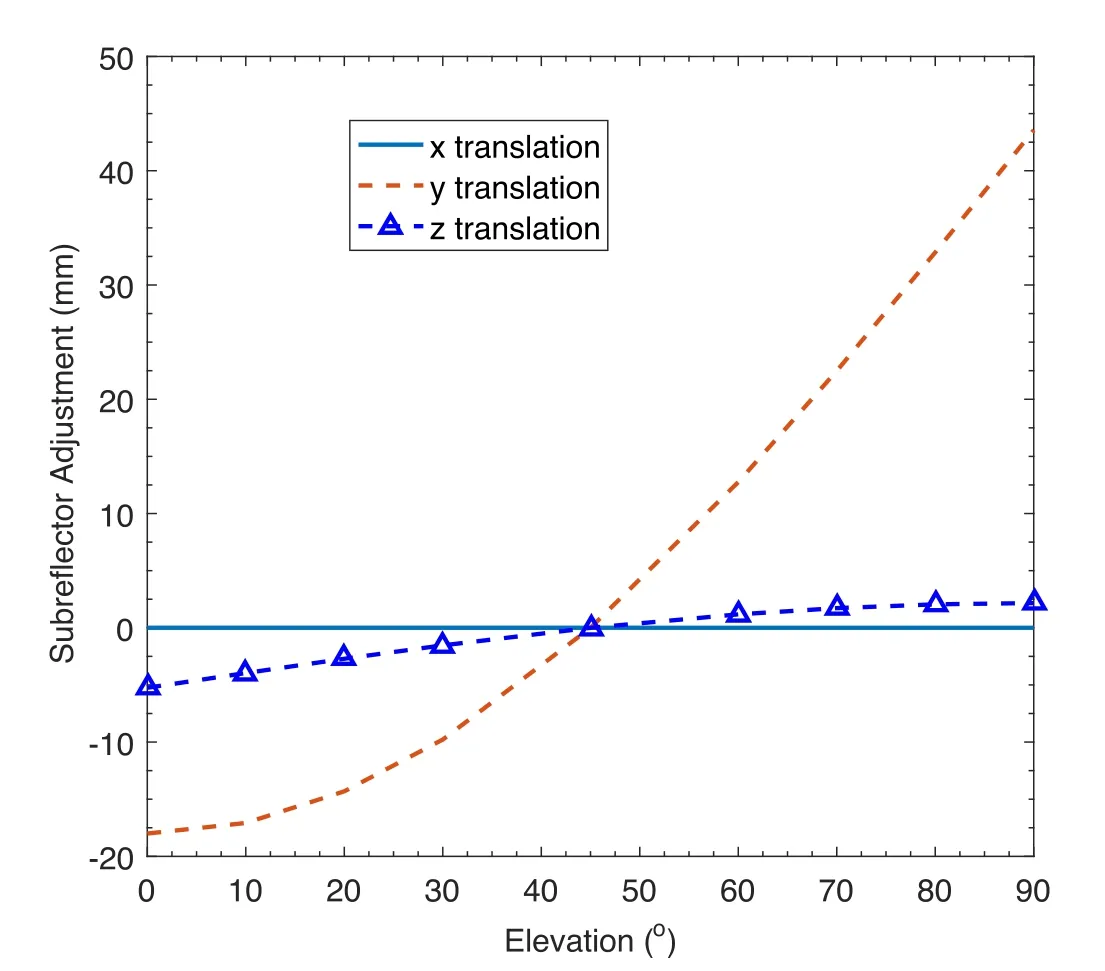
Figure 9.Variation of lateral translation x,y, and axial translation z of the subreflector with various elevation angles.

The total wavefront errors caused by subreflector displacements can be written as

where θ1,θ2,θ3are reference angles of the tilt,astigmatism,and coma caused by the subreflector displacements,respectively;the coefficients (A0–A5) are given by:

For circular aperture antennas,the PLD(or wavefront errors)can be described by Zernike circle polynomials as

where αiis the Zernike coefficient,andican be set as 21,which can be obtained by least squares fitting.According to the relationship between Seidel aberration coefficients and Zernike coefficients (Xiang et al.2019b),the Seidel aberration coefficientsbican be obtained by:b1=a1,b2=a3,b3=a2,b4=a5,b5=a6,b6=a4,b7=a9,b8=a8,b9=a13.Then,the aberration coefficients caused by subreflector displacements can be expressed with Zernike coefficients as:

4.Correction of the Primary Aberration by Adjusting Subreflector Position

It is pointed out in the previous section that subreflector displacement will cause the primary aberrations in cases such as piston,tilt,defocus,coma,and spherical aberration.The wavefront error produced by these aberrations over the antenna aperture is a function of the aperture coordinatesr′,θ′ and it can be calculated by Equation (9).One can always adjust the subreflector position to reduce the wavefront aberrations.

We can tell from the relationships of the subreflector displacements with the aberrations that the displacements of the subreflector position are determined by the decomposition between the wavefront errors and the primary aberrations.Therefore,for the wavefront caused by the antenna structural deformation,we can actively adjust the subreflector position to correct the main primary wavefront aberrations,such as the tilt,defocus,coma,and spherical aberration.Here,a new method of subreflector positional adjustment based on the aberration correction is proposed.

Let δ0be the wavefront error when the subreflector position is not adjusted,then the residual aberration with the subreflector adjustment can be given byδr=δ0+δ′,whereδ′ denotes the wavefront error induced by the subreflector adjustment.From Equation (4),the residual aberration can be expressed as

Given that the effect of the subreflector rotation is the same as lateral translation,here we only consider the axial and lateral translations of the subreflector to correct the aberration.

In order to eliminate the effects of the primary wavefront aberrations,the adjustment of the subreflector position must satisfy the condition that the residual primary aberrations are minimum,such that as δr→0,thenδ0≅-δ′.In the previous section,the relationships of aberration coefficients with the subreflector displacements are established from Equations (11)to (15).

For determining the adjustment of the subreflector position,one can fit the wavefront errors by the Zernike polynomial to obtain the coefficients,then calculate the aberration coefficients based on the Seidel aberration theory,and finally obtain the required amount of adjustment for the subreflector position by the relationship between the wavefront aberrations and the subreflector displacements.It is obvious that active adjustment of the subreflector can correct some primary aberrations,but astigmatism and high order aberrations cannot be corrected by the subreflector positional adjustment.

In this paper,we mainly consider correcting the wavefront aberrations which consist of all the tilt and defocus,and part of the coma and spherical aberration.To correct the defocus aberration from the subreflector by axial translation,we can determine the amount of adjustment for the subreflector in the axial direction by

Similarly,we can correct the tilt aberration to determine the amount of adjustment for the subreflector in the lateral direction by

The amount of adjustment for the subreflector axial and lateral translation can be obtained rapidly.After the subreflector axial adjustment,the defocus aberration can be corrected,that is,A2=0,and the part consisting of spherical aberration can also be corrected as

After the subreflector’s lateral adjustment,the tilt aberration can be corrected,that is,A1=0,and the part consisting of coma aberration can also be corrected as

with the reference angle at θ1.

From Equations (23) to (24),we can estimate rapidly the amount of adjustment for the subreflector’s lateral and axial translation under the current working condition;through this adjustment,some primary aberrations can be corrected,such as the tilt and defocus,and there is some residual coma,spherical aberration,and astigmatism.

5.Example Illustrating Correction of Wavefront Primary Aberrations with Adjusting the Subreflector Position

To verify the validity and effectiveness of a new method of subreflector adjustment based on correction to the primary aberrations,a computer program presented above has been developed,which can compute the primary aberration distribution and the positional adjustment of the subreflector when there are structural deformations induced by gravity.The data of gravity deformations are obtained by finite element analysis.The adjustment values of the subreflector position are calculated in order to eliminate some aberrations and compensate the wavefront error by moving the subreflector.

An example of a dual-reflector antenna dealing with the subreflector adjustment to correct wavefront errors due to gravity deformations is performed.For a Cassegrain antenna with the scale of primary reflector diameterDp=25 m,subreflector diameterDs=3 m,focal lengthf=7.8 m,semimajor axis distance of subreflectora=2.25 m,and semi-focal length of subreflectorc=3.05 m,the geometry of the dualreflector is depicted in Figure 4.It is assumed that the antenna structure will deform which is induced by gravity load,so the primary reflector surface and subreflector are aligned in such a way that the antenna is pointing at some intermediate elevation angle EL0.The presented method in this paper will be used to determine the adjustment quality to correct wavefront errors.The antenna structural deformation induced by gravity is obtained by a finite element model.In this example,we consider the adjustment of the subreflector position in the axial and lateral directions only.The cases of reflector pointing at elevation angles between 0° and 90° are computed.

Figure 5 displays the wavefront errors induced by gravity deformations of the reflectors at 10°,45°,and 80°,and Figure 6 shows the residual wavefront errors with subreflector positional adjustment.It can be seen from the error figures that the wavefront errors due to gravity deformations of the reflectors are almost dominated by tilt and coma.After the subreflector position is adjusted,the errors are reduced significantly and the residuals are almost dominated by astigmatism and higher order aberrations.

For evaluating the effects of the subreflector displacements on the EMP,the gain loss is calculated(Xiang et al.2019b)and compared with the original one without the adjustment.The results at 10°,45°,and 80°are plotted in Figure 7.The results indicate that the method of adjusting the subreflector position exhibits some good performances.It can be seen that the beam pointing deviations induced by the reflector’s gravity deformation almost are eliminated,moreover,the gain losses and near sidelobes are reduced compared with the theoretical curve.The deviations of the far sidelobes are still significant.

Figure 8 shows the primary aberrations of the 25 m Cassegrain antenna when the position of the subreflector is adjusted and the reflector surface is aligned at a 45° elevation angle.The values of the lateral translationx,y,and of axial translationzfor various elevation angles are displayed in Figure 9.Considering that the piston has no effect on the aperture phase,its effect will not be considered here.The results indicate that the wavefront errors due to gravity without adjustment of the position of the subreflector have more influence on the tilt,defocus,and coma than astigmatism and spherical aberration,and astigmatism have the least influence.It is found from Figure 8(b) that after adjusting the position of the subreflector used by the proposed method,almost all the effects of tilt and defocus due to gravity deformation are corrected,and the effect of coma is corrected in part.The residual aberrations are very small.This affirms that the reflector distortion caused by gravity will mainly cause the first three-order wavefront aberrations,and significant wavefront aberrations may occur due to the subreflector positional displacement.Furthermore,the wavefront aberrations of a Cassegrain antenna may be reduced significantly by appropriate lateral translation and axial translation of the subreflector.

From the above results,it is found that suitable lateral and axial translations of the subreflector can effectively correct the effects of the tilt,defocus,and coma in the primary aberrations caused by gravity deformations,but the spherical aberration,astigmatism,and high order aberrations almost cannot be corrected by the subreflector motion,therefore,the deformable reflector may need to be used to correct the residual aberrations.

6.Conclusion

This paper proposes a new method of subreflector adjustment with wavefront aberration elimination.The characteristic of wavefront errors caused by subreflector displacement of a dual-reflector antenna has been studied,and the relationships between the positional displacement of the subreflector and the Seidel wavefront aberrations are derived.From these relationships,it is known that the subreflector axial translation will induce the aberration characteristics of spherical,defocus,and piston,the subreflector lateral translation will induce the aberration characteristics of tilt and coma,and the subreflector tilt will induce the aberration characteristic of tilt and coma.The relationships of the aberration coefficients with the subreflector displacements are linear.The subreflector tilt has the same effect on aberration with the subreflector lateral translation.With the same amounts of displacement of the subreflector position,it has a greater influence on the tilt and defocus of the wavefront aberrations.

Based on the relationships between positional motions of the subreflector and Seidel wavefront aberrations,we present a method of correcting the wavefront aberrations to determine the amount of adjustment for the subreflector position rapidly in order to compensate the structural deformation induced by gravity.The results of an example demonstrate that suitable lateral and axial translations of the subreflector can effectively correct the effects of the first three primary aberrations caused by gravity deformations.Still,other high order primary aberrations almost cannot be corrected by positional adjustments of the subreflector.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (NSFC,Grant No.U1931137) and the National Key Basic Research Program of China(2018YFA0404702).

ORCID iDs