The Oblique Alfvén Ion Beam Instability in the Earthʼs Ion Foreshock

Yuhang Yao,Jinsong Zhao,Huasheng Xie,Wen Liu,and Dejin Wu

1 Key Laboratory of Planetary Sciences,Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210023,China;js_zhao@pmo.ac.cn

2 School of Astronomy and Space Science,University of Science and Technology of China,Hefei 230026,China

3 Hebei Key Laboratory of Compact Fusion,Langfang 065001,China

4 ENN Science and Technology Development Co.,Ltd.,Langfang 065001,China

Abstract How ions evolve in the Earth’s ion foreshock is a basic problem in the heliosphere community,and the ion beam instability is usually proposed to be one major mechanism affecting the ion dynamics therein.This work will perform comprehensive analyses of the oblique ion beam instability in the Earth’s ion foreshock.We show that in addition to two well-known parallel instabilities (i.e.,the parallel fast-magnetosonic whistler instability and the parallel Alfvén ion cyclotron instability),the oblique Alfvén ion beam (OA/IB) instability can also be triggered by free energy relating to the relative drift dV between the solar wind proton and reflected proton populations.For slow dV (e.g., dV ≾2.2VA,where VA denotes the Alfvén speed),it only triggers the OA/IB instability.When dV ≿2.2VA,the growth rate in the OA/IB instability can be about 0.6 times the maximum growth rate in parallel instabilities.Moreover,this work finds the existence of two types of OA/IB instabilities.The first one appears at slow dV and in the small wavenumber region at fast dV,and this instability can be described by the cold fluid model.The second one arises in large wavenumber regions at fast dV,and this instability only appears in warm plasmas.Furthermore,through the energy transfer rate method,we propose that the OA/IB instability is driven by the competition among the Landau and cyclotron wave-particle interactions of beam protons,the cyclotron wave-particle interaction of core protons,and the Landau wave-particle interaction of electrons.Because oblique waves can experience significant damping,the importance of the OA/IB instability may be the effective heating of ions in the Earth’s foreshock.

Key words: plasmas–instabilities–waves–(Sun:) solar-terrestrial relations

1.Introduction

The Earth’s bow shock is generated by the interaction of the solar wind with the Earth’s magnetosphere (e.g.,Eastwood et al.2005;Yang et al.2016;Lu et al.2020).Upstream of the bow shock,there exists a region known as the foreshock,filled with incident solar wind particles and particles reflected by the bow shock(e.g.,Eastwood et al.2005).In addition to particles,the Earth’s foreshock also contains prevailing ultra-low frequency (ULF) waves and large-scale structures,e.g.,shocklets,and short large-amplitude magnetic structures(SLAMS) (e.g.,Hada et al.1987;Scholer 1993;Scholer et al.2003;Tsubouchi &Lembège 2004).Similar to the bow shock,shocklets and SLAMS can reflect a part of solar wind ions,forming beams propagating in the anti-Earth direction in the foreshock region(e.g.,Scholer&Burgess 1992;Wilkinson et al.1993;Mann et al.1994;Wilson et al.2013).These reflected ions can further become diffuse superthermal ions through acceleration in the interactions with ULF waves and/or in the trapping between upstream ULF waves and the shock front (e.g.,Su et al.2012;Wu et al.2015;Hao et al.2016,2021).

Due to free energy relating to the relative drift between incident solar wind ions and reflected ions,the instability can be easily triggered,and previous instability analyses predict the existence of three types of electromagnetic instabilities in the foreshock region (e.g.,Sentman et al.1981;Winske &Leroy 1984;Gary&Tokar 1985;Gary et al.1986;Gary 1991;Akimoto et al.1993;Malovichko et al.2018): right-hand resonant instability,right-hand non-resonant instability,and left-hand resonant instability.The three instabilities are dominated at different ion beam conditions (e.g.,Sentman et al.1981;Winske&Leroy 1984;Gary 1991;Wilson 2016).The right-hand resonant instability can be preferentially excited by tenuous ion beams withVi≿VA(e.g.,Sentman et al.1981;Winske &Leroy 1984;Gary 1991),whereVidenotes the drift speed of the ion beam,andVAdenotes the Alfvén speed.The right-hand non-resonant instability is dominantly produced by cool and dense ion beams with large drift speeds (Vi≫VA),(e.g.,Sentman et al.1981;Winske &Leroy 1984;Gary 1991).The left-hand resonant instability can mainly be driven by warm ion beams withVi≿VA(e.g.,Gary 1991).Because these instabilities drive the waves with different mode natures,e.g.,the parallel fast-magnetosonic whistler wave in the right-hand resonant instability(e.g.,Gary 1991),the firehose mode wave in the right-hand non-resonant instability (e.g.,Winske &Leroy 1984),and the Alfvén ion cyclotron wave in the left-hand resonant instability(e.g.,Gary 1991),they are named as the parallel fast-magnetosonic whistler(PFM/W)instability,the firehose-like instability,and the parallel Alfvén ion cyclotron (PA/IC) instability in this study.

According to the preferential excitation condition of each instability,the two ion beam populations (i.e.,reflected ions and diffuse ions) in the ion foreshock can trigger different instabilities.Because reflected ions are relatively cool and their drift speed is much larger than the local Alfvén speed(e.g.,Bonifazi&Moreno 1981a,1981b;Kucharek et al.2004;Kucharek 2005;Miao et al.2009;Wilson et al.2013),these ions can drive the PFM/W instability and/or the firehose-like instability (e.g.,Winske &Leroy 1984;Gary 1991).For diffuse ions,compared to reflected ions,they exhibit hotter temperature and slower drift speed (e.g.,Bonifazi &Moreno 1981a,1981b;Kis 2004;Kis et al.2007;Wilson et al.2009;Meziane et al.2011),and they preferentially produce the PFM/W instability and/or the PA/IC instability(e.g.,Winske&Leroy 1984;Gary &Tokar 1985).The PFM/W instability induced by diffuse ions is often proposed to be the excitation mechanism of large-amplitude ULF waves in the ion foreshock.

Actually,in addition to the aforementioned parallel instabilities,the ion beam can easily trigger two types of oblique instabilities,i.e.,the oblique Alfvén ion beam (OA/IB) instability (e.g.,Daughton &Gary 1998;Daughton et al.1999;Lu et al.2006,2009;Liu et al.2021) and the oblique fast-magnetosonic whistler instability(e.g.,Montgomery et al.1976;Liu et al.2021).In particular,the OA/IB instability,which is generated as the Alfvén ion cyclotron mode wave and the ion beam mode wave are coupled together (Liu et al.2021),is believed to be one of two main types of ion instabilities in solar wind environments (Daughton &Gary 1998;Liu et al.2021).However,to our knowledge,comprehensive analyses of oblique instabilities are not yet performed under the plasma parameters representing the Earth’s ion foreshock environment.Hence,their importance in the Earth’s ion foreshock is still unknown.

This paper will perform a preliminary analysis of the oblique ion beam instability in the Earth’s ion foreshock environment.We exhibit the existence of the OA/IB instability with the growth rate being of the order of that in parallel ion beam instabilities,and we also find one new type of the OA/IB instability that is not reported yet.The rest of this paper is structured as follows.Section 2 introduces the model and method we used.Section 3 exhibits our results.Section 4 contains the conclusion and discussion.

2.Model and Method

We consider an ideal model consisting of a core proton,beam proton,and electron components,where the two former components are used as proxies of incident solar wind protons and reflected protons in the Earth’s ion foreshock.These particle populations are assumed to follow the drifting Maxwellian distribution,i.e.,

wherensdenotes the number density,denotes the parallel thermal speed,denotes the perpendicular thermal speed,Vsdenotes the drift speed,msdenotes the mass,andTs∥andTs⊥denote the parallel and perpendicular temperatures for the species “s” (“pc” proton core,“pb” proton beam,and “e” electron),respectively.We also assume all particles have isotropic temperatures,i.e.,Ts∥=Ts⊥=Ts.In this paper,for the proton core(the solar wind proton population),the plasma parameters arenpc=15 cm−3andTpc=2.5 eV.The number density and temperature of the moderate dense proton beam (the reflected proton population)are assumed asnpb=npc/2 andTpb=Tpc.We also performed the instability analyses in the case ofnpb=npc/9 and obtained results similar to the case ofnpb=npc/2 used in this paper.For the electron population,we assume thatne=npc+npbandTe=Tpc.This study considers a varying drift speed of the proton beamVpbto perform a comparison between parallel and oblique ion beam instabilities.Based on the proton core frame whereVpcis zero,the zero-current condition leads to the relation ofnpbVpb=neVe.Besides,the background magnetic field strength used in this paper isB0=7 nT.

Because charged particles are weakly collisional in the foreshock,the Vlasov equation can be used to describe the particle dynamics therein.Combining the Vlasov equation and Maxwell’s equations,the wave dynamics is controlled by the following equation

and the solutions correspond to the eigenmodes of plasma waves.Here,k is the wavevector,ω is the wave frequency,E is the wave electric field,∊is the dielectric tensor,andcis the light speed.This study uses a newly developed numerical solver BO/PDRK (Xie &Xiao 2016;Xie 2019)to perform the instability analysis,and the most advantage of this solver is that all unstable wave modes can be found at the same time.

One key problem in the instability study is which mechanism contributes to the instability excitation.Recently,an energy transfer rate method has been developed to quantify wave-particle interactions for stable and unstable waves (Liu et al.2021;Zhao et al.2022).This method is helpful for analyzing different wave-particle interaction mechanisms,and it was applied to study the ion kinetic instability in the solar wind (Liu et al.2021).This paper will use this method to analyze the ion beam instability in the Earth’s ion foreshock.Using Equation(2) and Maxwellian’s equations,we can calculate energy transfer rates between unstable waves and particles through the following expressions

whereWEBdenotes the electromagnetic energy of the wave,J denotes the current density,J∥(J⊥)denotes the current density in the parallel (perpendicular) direction,and E∥(E⊥) denotes the electric field in the parallel (perpendicular) direction.The superscript “*” denotes the complex conjugate.Moreover,we will use the energy transfer rate in velocity space to show more details of the oblique ion beam instability (the method for calculating such energy transfer rate is explained by Zhao et al.2022).

3.Results

3.1.Parallel Versus Oblique Ion Beam Instabilities

In order to exhibit the differences between parallel and oblique ion beam instabilities triggered in the ion foreshock environment,Figure 1 presents the distributions of the maximum growth rate γm(normalized by Ωcp),the wave frequency ωr(normalized by Ωcp),and the argument arg (EyEx) of the ratio between two electric field componentsEyandEx.From two-dimensionalVpb−θ distributions shown in Figures 1(a)–(c),we clearly see the existence of three types of ion beam instabilities that have different characteristics of ωr/Ωcpand arg (Ey).The PA/IC and PFM/W instabilities produce the left-hand waves with arg (EyEx)=-90° and the right-hand waves with arg (EyEx)=90°,respectively.These two parallel instabilities also generate waves that have different frequencies,i.e.,ωr<Ωcpin the PA/IC instability and ωr≿Ωcpin the PFM/W instability.The oblique instability arising at large θ corresponds to the OA/IB instability clarified by Liu et al.(2021).This instability produces the waves with ωr<Ωcpand with highly varying arg (EyEx).The latter is strongly dependent on θ.For example,the excited nearperpendicular waves behave as the linear polarization,i.e.,arg

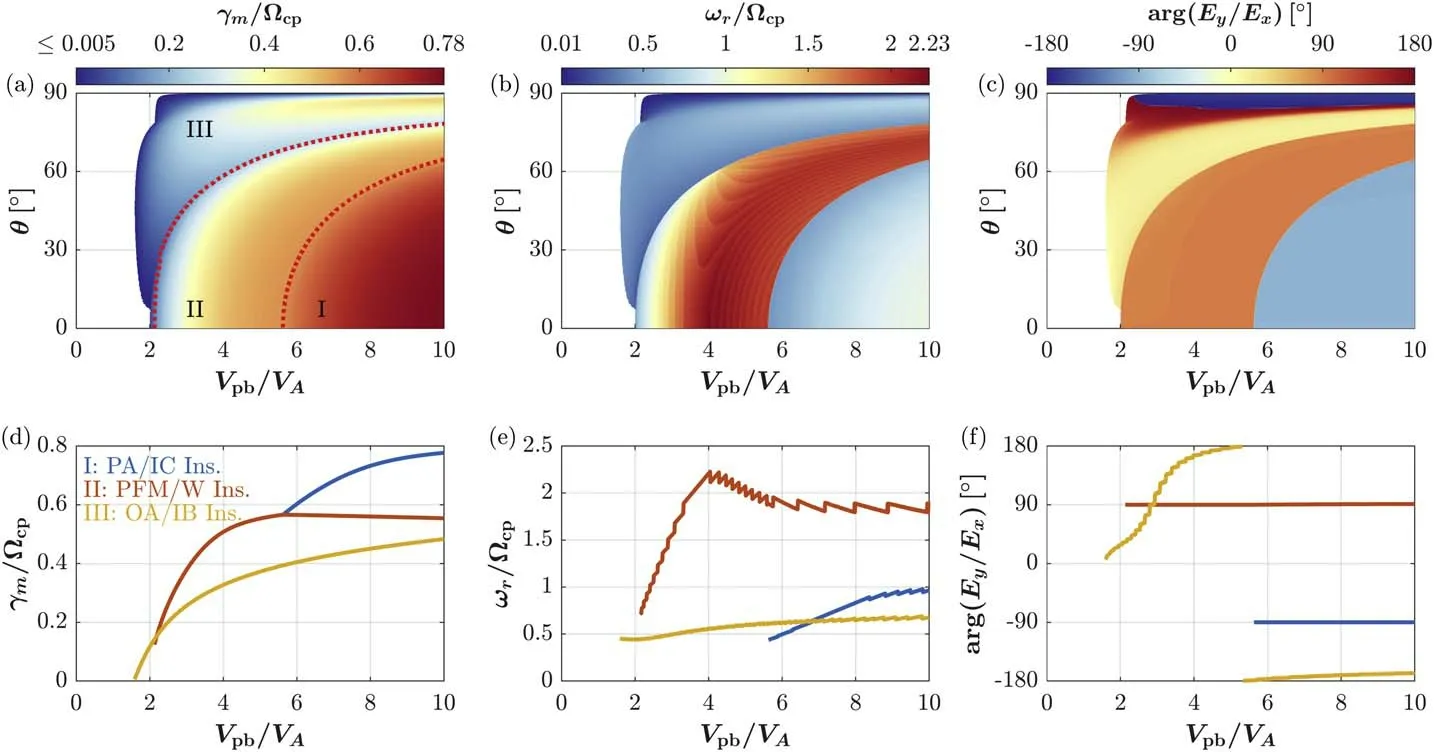
Figure 1.Parallel and oblique ion beam instabilities.(a) The maximum growth rate γm (normalized by the proton cyclotron frequency Ωcp) as functions of the drift speed of the proton beam Vpb and the wave normal angle θ.(b) The distribution of the real frequency ωr (normalized by Ωcp) in Vpb −θ space.(c) The argument arg (E y Ex)of the ratio of two electric field components Ey and Ex in Vpb −θ space.(d)The maximum γm at each Vpb for three ion beam instabilities.(e)ωr at positions of γm in panel(d).(f)arg (Ey Ex)at positions of γm in panel(d).The symbols“I”,“II”,and“III”denote the PA/IC instability,the PFM/M instability,and the OA/IB instability,respectively.The dotted curves in panel (a) label the boundaries among the three instabilities.

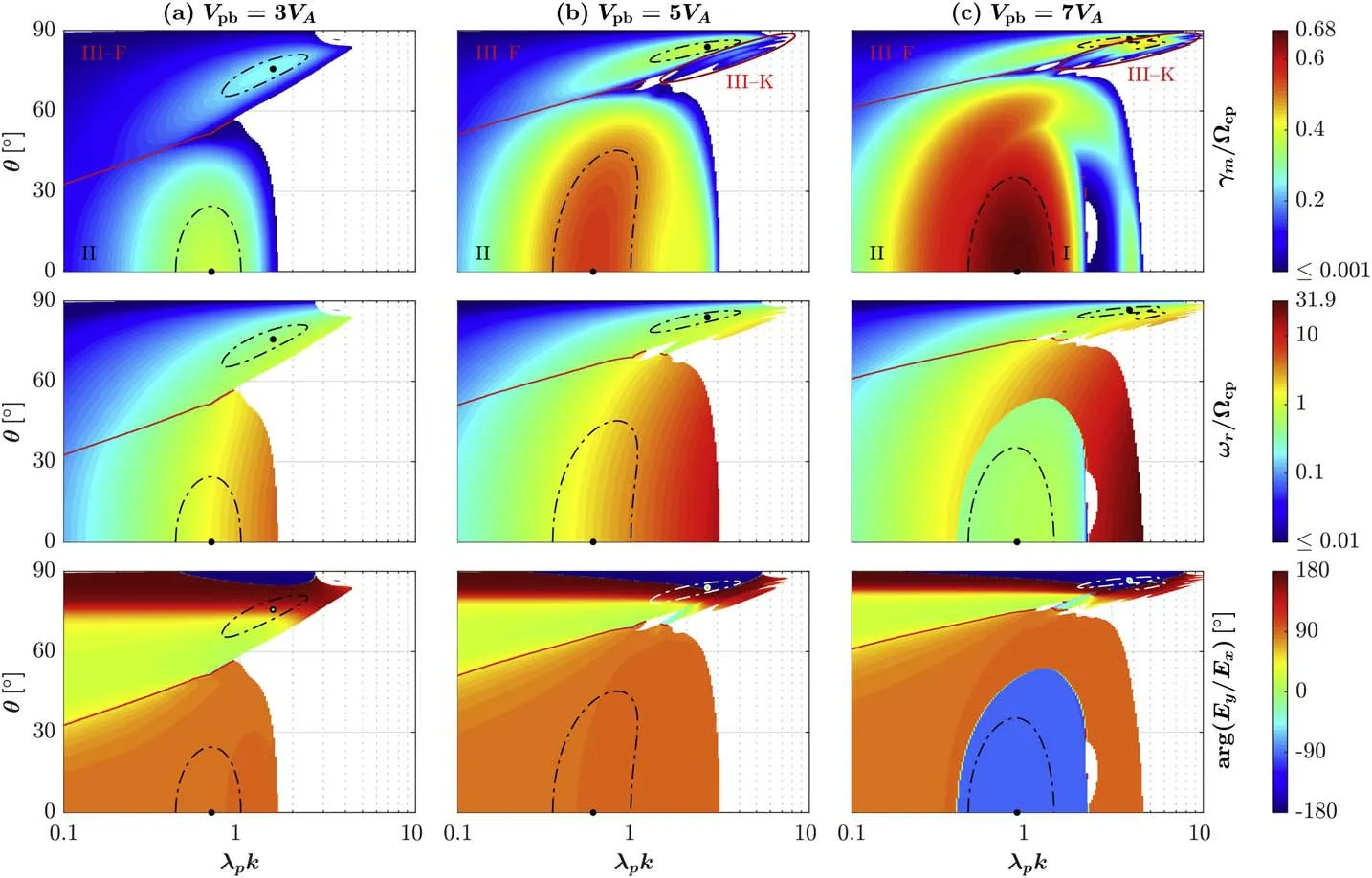
Figure 2.The k −θ distributions of parallel and oblique ion beam instabilities driven by proton beams with (a) Vpb=3VA,(b) 5VA,and (c) 7VA.(Top panels) the maximum growth rate γm normalized by Ωcp;(middle panels)the normalized real frequency ωr/Ωcp at positions of γm;and(bottom panels)the argument of Ey/Ex at positions of γm.The black points label the maximum growth rate γm in each type of instability,and the dashed–dotted curves label the contour lines of γ=0.9γm.I=the PA/IC instability;II=the PFM/W instability;III-F=the OA/IB-F instability;and III-K=the OA/IB-K instability.

Figures 1(d)–(f)present the distributions of γm/Ωcp,ωr/Ωcp,and arg (Ey) at positions of the maximum γm/Ωcpat eachVpb.The PFM/W and PA/IC instabilities are strongest in the parallel propagation,and θ associated with the strongest OA/IB instability varies withVpb,e.g.,θ ∼60° atVpb=2VAand θ ∼87° atVpb=10VA.From Figure 1(d),one interesting finding is that the OA/IB instability is the dominant instability as the proton beam is relatively slow,i.e.,Vpb≃1.8–2.2VA,and the growth rate of this instability is about 0.6 times the maximum growth rate in the parallel instability asVpb≿2.2VA.Consequently,the OA/IB instability can experience considerable growth in the case of fast beaming protons.

Figure 2 compares the OA/IB instability to the two parallel instabilities triggered by the proton beam with three different drift velocities,i.e.,Vpb=3VA,5VA,and 7VA.This figure exhibits that the transition from the PFM/W instability into the OA/IB instability arises at large θ.This transition is evident in the distribution of γm/Ωcpbut not in ωr/Ωcpand arg (EyEx)distributions,and the transition normally corresponds to the minimum γm/Ωcpat eachk.Moreover,this transition occurs at larger θ for largerVpb.Compared to the unstable region in the OA/IB instability triggered byVpb=3VA(Figure 2(a)),the unstable regions atVpb=5VAand 7VAcan be separated into two parts (labeled by III-F and III-K in Figures 2(b) and (c)).As explained in the following subsections,the III-F region roughly coincides with the unstable region under the cold plasma condition in which the waves follow the fluid behavior,and the III-K region is mainly induced by kinetic effects such as cyclotron wave-particle interactions.

Figure 3.The unstable and related stable mode waves in parallel and oblique ion beam instabilities driven by proton beams with(a)Vpb=3VA,(b)5VA,and(c)7VA under the cold plasma condition.From top to bottom,θ=0°,50°,70°,and 75°.The labels with yellow and green colors denote the waves propagating forward and backward direction in plasmas where Vpb is zero.I=the PA/IC instability;II=the PFM/W instability;and III-F=the OA/IB-F instability.AIBW=the Alfvén Ion Beam mode Wave;AICW=the Alfvén Ion Cyclotron mode Wave;and FMWW=the Fast-Magnetosonic Whistler mode Wave.

3.2.Generation Mechanism of the OA/IB Instability

For understanding the generation mechanism of the OA/IB instability,we follow the method introduced by Liu et al.(2019)and Liu et al.(2021).We will first show the dispersion relations of unstable waves at the cold plasma condition,which will provide useful clues to exhibit the generation mechanism in the fluid model.Figure 3 presents such results in the OA/IB instability and two parallel instabilities at the cold plasma condition.We note that due to the effect of the ion beam,the backward propagating Alfvén ion cyclotron mode wave can couple with the ion beam mode,and this results in a coupled wave mode that is named the Alfvén ion beam mode wave (Liu et al.2021).In order to give a clear description for the wave-wave coupling in Figure 3,we use “forward” and“backward” to label the wave which propagates forward or backward relative to the background magnetic field in plasmas whereVpbis zero.

Figure 3(a) shows the unstable and related stable waves at four typical angles in ion beam instabilities triggered atVpb=3VA.This figure shows that the PA/IC and PFM/W instabilities arise at θ=0°.The former is induced by the coupling between forward Alfvén ion cyclotron and backward fast-magnetosonic whistler mode waves,and the latter results from the coupling between forward fast-magnetosonic whistler and backward Alfvén ion beam mode waves.When θ=50°,the backward Alfvén ion beam mode wave,which decouples with the forward fast-magnetosonic whistler mode wave,couples with the forward Alfvén ion cyclotron wave at small λpk,inducing the OA/IB instability,and the PFW/W instability still exists at large λpk.At larger θ,e.g.,θ=70°and 75°,the PFW/W instability disappears,and only the OA/IB instability exists.

Figure 4.An example for showing the unstable and related stable mode waves with θ=80°at(a)Vpb=3VA,(b)5VA,and(c)7VA in warm and cold plasmas.(Top panels) The dispersion relations overlaid the color representing the growth rate γ in warm plasmas;(middle panels) the dispersion relations overlaid the color representing the polarization information in warm plasmas;and(bottom panels)the dispersion relations overlaid the color representing γ in cold plasmas.AIBW=the Alfvén Ion Beam mode Wave;AICW=the Alfvén Ion Cyclotron mode Wave;and FMWW=the Fast-Magnetosonic Whistler mode Wave.

Similar to theVpb=3VAcase,Figures 3(b)and(c)show the unstable and related stable waves atVpb=5VAand 7VA,respectively.These two figures exhibit the coupling between the backward Alfvén ion beam and forward Alfvén ion cyclotron waves arising at larger θ for largerVpb.Therefore,the OA/IB instability occurs at larger θ for largerVpb.

Although the OA/IB instability can arise in cold plasmas,the lack of the kinetic effect (i.e.,wave-particle interactions)makes such a theoretical prediction to be incomplete.To show this incompleteness,Figure 4 exhibits the OA/IB instability under both cold and warm plasma conditions.AtVpb=3VA,the unstable region in cold plasmas is nearly consistent with that in warm plasmas,as shown in Figure 4(a).We also find the coupling of the two wave modes to be responsible for the instability predicted from cold plasmas.This is the reason for labeling this unstable region as the OA/IB-F region,in which the instability is mainly controlled by the fluid behaviors in cold plasmas.At largeVpb,i.e.,Vpb=5VAand 7VAshown in Figures 4(b) and(c),the unstable regions at large λpkin warm plasmas are beyond the predictions in cold plasmas,and the unstable waves are connected to fast-magnetosonic whistler mode waves which are not predicted by the cold plasma model.Actually,the kinetic effects dominate the unstable region at large λpkin warm plasmas,and we hence label this region as the OA/IB-K region to emphasize the role of kinetic effects.

Figure 5.The energy transfer rate in the OA/IB-F and OA/IB-K instabilities triggered at Vpb=5VA and θ=80°:(a)the total energy transfer rate,Ps;(b)the parallel energy transfer rate,Ps∥;and(c)the perpendicular energy transfer rate,Ps⊥.The solid and dotted curves denote the OA/IB-F and OA/IB-K instabilities,respectively.The blue,red,and yellow colors denote the energy transfer rate of the proton beam,proton core,and electron component,respectively,and the black color denotes the net energy transfer rate.The circuses label the positions of the maximum growth rates in OA/IB-F and OA/IB-K instabilities.

3.3.Energy Transfer Rates in the OA/IB Instability

Using the energy transfer rate method introduced by Liu et al.(2021),we can quantify wave-particle interactions between unstable waves and particles.Therefore,this method can explore the generation mechanism responsible for the OA/IB-F and OA/IB-K instabilities.

Figure 5 presents the distributions of totalPs,parallelPs∥,and perpendicularPs⊥energy transfer rates in the OA/IB instability triggered atVpb=5VAand θ=80°.This figure evidently exhibits the energy flowing channel: energy flowing from the proton beam population into unstable waves(Ppb<0),and then a part of the energy of unstable waves flowing into the proton core and electron populations (Ppc>0 andPe>0).Owning toPe∥>Ppc∥shown in Figure 5(b) andPpc⊥>Pe⊥shown in Figure 5(c),electrons gain more energy than core protons in the parallel direction,whereas the latter gain more energy than the former in the perpendicular direction.The most interesting finding is thatPpc⊥would be larger thanPpb⊥in the whole OA/IB-K regime and at largekin the OA/IB-F regime,which induces the loss of wave energy in the perpendicular direction.Therefore,we propose that the excitation of the OA/IB instability is determined by the interplay of Landau and cyclotron type wave-particle interactions relating to beam protons,Landau type waveparticle interaction of electrons,and cyclotron type waveparticle interaction of core protons.

One important consequence of the instability is the redistribution of energy.To show this consequence,Figures 6 and 7 present the energy transfer rates in velocity space at the strongest instability in OA/IB-F and OA/IB-K regimes shown in Figure 5.Both instabilities induce a similar distribution in the velocity space: the loss of energy for beam protons atvpb∥≃9VTpb∥,and the gain of energy for core protons atvpc∥=0 and for an electron atve∥=0.However,the obvious difference between OA/IB-F and OA/IB-K instabilities occurs in the distributions ofPpb⊥(v∥,v⊥)andPpc⊥(v∥,v⊥).Compared to Figures 6(a3)and(b3)in which nearly all beam protons emit energy and all core protons absorb energy in the OA/IB-F instability,beam protons withvpb∥≾9VTpb∥can absorb energy and core protons withvpb∥≿1.6VTpb∥can emit energy in the OA/IB-K instability,as shown in Figures 7(a3)and(b3).This elaborate variation of the energy transfer is mainly controlled by the perturbed proton distribution function in velocity space,in which the terms relating to the Bessel function are highly varying at largerk⊥v⊥/Ωcpas explored in Zhao et al.(2022).

Figure 6.The two-dimensional v∥−v⊥distributions of the energy transfer rate in the strongest OA/IB-F instability shown in Figure 5:from top to bottom,the proton beam,the proton core,and the electron component.(a1,b1,and c1)The total energy transfer rate,Ps(v∥,v⊥);(a2,b2,and c2)the parallel energy transfer rate,Ps∥(v∥,v⊥);and (a3,b3,and c3) the perpendicular energy transfer rate, Ps⊥(v∥, v⊥).The data are normalized by the maximum |Ppb|,and the values labeled in each panel denote the energy transfer rate integrated in velocity space.

4.Conclusion and Discussion

This work focuses on the oblique ion beam instability in the plasma environment being a proxy of the Earth’s ion foreshock.We exhibit that in addition to the two parallel instabilities,i.e.,the PA/IC instability and the PFM/W instability,the OA/IB instability can control the excitation of the waves at large θ.We also exhibit that the OA/IB instability is the only single instability triggered by the slow proton beam withVpb≃1.8–2.2VA,and this instability would have a considerable growth rate (about 0.6 times of the maximum growth in the parallel instabilities) asVpb≿2.2VA.Different from circularly polarized unstable waves excited in the parallel instabilities,the OA/IB instability produces the waves mainly behaving as the linear polarization.

This work finds the existence of two types of OA/IB instability,i.e.,the OA/IB-F instability and the OA/IB-K instability.Normally,the OA/IB-F type instability arises in the smallkregion,and this instability can be roughly described by the fluid model(under the cold plasma condition that excludes kinetic wave-particle interactions).The OA/IB-K instability arises in the largekregion,which merely arises in warm plasmas where kinetic wave-particle interactions are included.We also show that the unstable wave in the OA/IB-F instability nearly corresponds to the coupling mode wave between the Alfvén ion cyclotron mode wave and the Alfvén ion beam mode wave,and the unstable wave in the OA/IB-K instability is associated with the coupling mode wave of the fast-magnetosonic whistler mode wave with the ion beam mode wave.

Moreover,this paper analyzes the energy transfer rate in two typical OA/IB-F and OA/IB-K instabilities.We explore that the instability excitation is mainly determined by the interplay of Landau and cyclotron-type wave-particle interactions of beam protons,cyclotron-type wave-particle interaction of core protons,and Landau-type wave-particle interaction of electrons.One major difference between OA/IB-F and OA/IB-K instabilities is that the energy emission of beam protons exceeds the energy absorption of core protons in the perpendicular direction (due to cyclotron-type waveparticle interaction) in the OA/IB-F instability,whereas the former is lower than the latter in the OA/IB-K instability.We also exhibit the energy transfer in the velocity space,which clearly shows how energy flows among different particle populations.

The finding of two types of OA/IB instability improves our understanding of ion beam instability (e.g.,Daughton &Gary 1998;Daughton et al.1999;Lu et al.2009;Liu et al.2021).Compared to previous studies of the OA/IB instability in the solar wind environments (e.g.,Daughton &Gary 1998;Liu et al.2021),because the relative speeds between the core and beam ions therein roughly distribute in the range of 0.5–2VA(e.g.,Marsch &Livi 1987;Ďurovcová et al.2019),only the OA/IB-F type instability is explored via instability analyses by Daughton&Gary (1998)and Liu et al.(2021).The OA/IB-K instability arises at a large streaming speed of the proton beam population (e.g.,Vpb>3VA,see Figure 4),which implies that this instability would be excited in the Earth’s ion foreshock environment whereVpbcan be 10VA(e.g.,Wilson 2016).

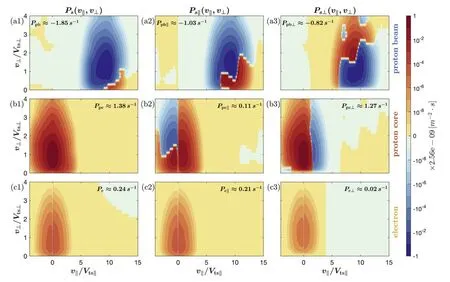
Figure 7.The two-dimensional v∥−v⊥distributions of the energy transfer rate in the strongest OA/IB-K instability shown in Figure 5:from top to bottom,the proton beam,the proton core,and the electron component.The descriptions for each panel are the same as those in Figure 6.

Our theoretical results imply that reflected ions and diffuse ions can trigger the OA/IB instability in the Earth’s foreshock.The importance of this instability is the effective energization of solar wind ions by the excited waves which have a frequency residing at about 0.5–2Ωcp.Also,these waves can scatter the reflected ions similar to the roles of other kinds of waves.Because the excited waves are obliquely propagating,they may experience damping more rapidly than the parallel waves triggered by parallel instabilities proposed in previous works.One may be interested in the problem of whether the waves excited by the OA/IB instability were reported in previous observational works.According to the frequency of the excited waves(∼0.5–2Ωcp)being roughly consistent with“30 s waves”(in whichf∼0.01–5Ωcpin the plasma frame,see Wilson 2016),we compared the features of the waves excited by the OA/IB instability with that of “30 s waves” summarized by Wilson(2016),and we concluded that they are totally different because the latter is the magnetosonic wave mode which is proposed to be produced by the right-hand resonant ion/ion instability (e.g.,Wilson 2016).Therefore,to our knowledge,previous observational works did not report the waves produced by the OA/IB instability in the ion foreshock,and the reasons for these waves being untraceable may be due to two facts,i.e.,(1) these waves can experience significant damping as they propagate outside their excitation source,and(2) the mixing of these waves with the waves excited by the parallel instabilities (i.e.,PA/IC and PFM/W instabilities)would result in the former being suppressed by the latter.Lastly,we note that the particle-in-cell and hybrid simulations could provide direct evidence for the excitation and evolution of the OA/IB instability in the ion foreshock,which will be performed in the future.

Acknowledgments

This work was supported by the National Key R&D Program of China 2021YFA1600502 (2021YFA1600500) and the NSFC 41974203.The author YHY appreciates the discussions with Dr.Yufei Hao.

ORCID iDs