突出数学核心概念 凸显核心素养导向——2022年中考“随机事件的概率”专题命题分析

杨 军，刘 栋

（山东省济南教育教学研究院；山东省济南稼轩学校）

《义务教育数学课程标准（2022年版）》（以下简称《标准》）的颁布，驱动了考试评价从能力立意向素养立意的转变.“随机事件的概率”是初中数学学习的重点内容之一，属于“统计与概率”领域的一个主题.从2022年全国各地区中考“随机事件的概率”相关试题的设计来看，更加关注对随机现象的考查，强调用定量的方法刻画随机事件发生可能性的大小，重点考查学生的数据观念、模型观念和应用意识.文章结合《标准》的要求，在对60份选自全国各地区的2022年中考试卷中“随机事件的概率”试题的各项数据进行统计、分析和整理的基础上，归纳了中考“随机事件的概率”试题的主要特点和命制思路，并对2023年中考备考提出一些建议.

一、考查内容分析

随机事件的概率是对随机现象的定量描述.随机现象的特征是可能发生也可能不发生，且发生的可能性大小不确定.但是许多随机现象发生的可能性大小是可以预测的.这是一种不确定的思维方式，主要培养学生从不确定的角度观察现实世界的能力.《标准》对此部分内容的要求是：（1）能通过列表、画树状图等方法列出简单随机事件所有可能的结果，以及指定随机事件发生的所有可能结果，了解随机事件的概率；（2）知道通过大量重复试验，可以用频率估计概率.

2022年全国各地区中考“随机事件的概率”试题普遍选取了丰富的设问情境，从不同角度对“随机事件的概率”内容进行了全面考查，如表1所示.主要考点有三个：（1）随机事件的相关概念及随机现象的特点；（2）运用概率的古典定义求事件的概率；（3）从数据分析的角度用频率估计概率.相关试题注重两步试验概率的计算，经常与统计知识一起考查，用频率估计概率的考查占比最小，随机事件概念的考查较往年略有下降.

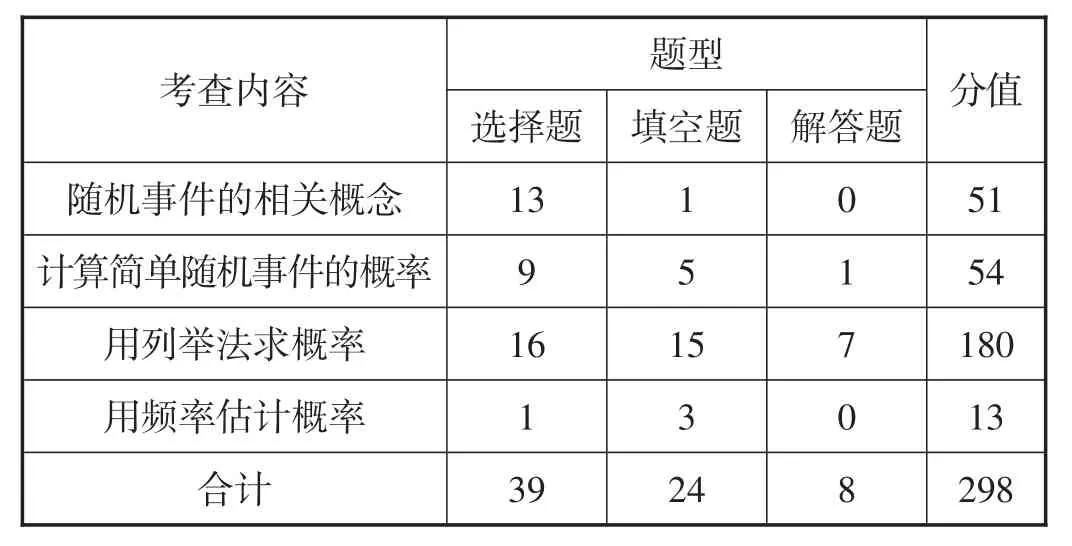
表1 60份试卷中“随机事件的概率”试题考查内容与题型

抽样的2022年全国各地区中考“随机事件的概率”试题涉及选择题、填空题和解答题.其中，填空题约占36.2%，选择题约占25.2%，解答题约占38.6%.填空题和选择题主要考查学生随机事件的概率相关的基础知识和基本技能，以及对随机事件的概率相关概念的简单应用；解答题则侧重考查学生综合运用随机事件的概率相关知识的能力.从分值来看，全国各地区中考数学试卷的满分多为120分或150分，在抽样的60份的试卷中，“随机事件的概率”试题的总分值为298分，对于卷面总分的平均占比为3.81%.其中，占比超过5%的试卷有21份，占比低于3%的试卷有26份.总体来看，所占比值与《标准》要求的“随机事件的概率”课时占比基本相符.

2022年中考“随机事件的概率”试题的考查内容涉及多种数学思想和方法.例如，在“摸球”过程中以“放回”与“不放回”为基本数学模型，考查学生的建模思想和分类讨论思想.该部分内容还涉及对学生数据观念、模型观念、应用意识、创新意识、运算能力等素养的考查.对2022年全国各地区中考“随机事件的概率”试题中涉及核心素养情况的统计如图1所示，其中考查模型观念占比最多，说明建立古典模型求概率仍然是此部分内容考查的重点.

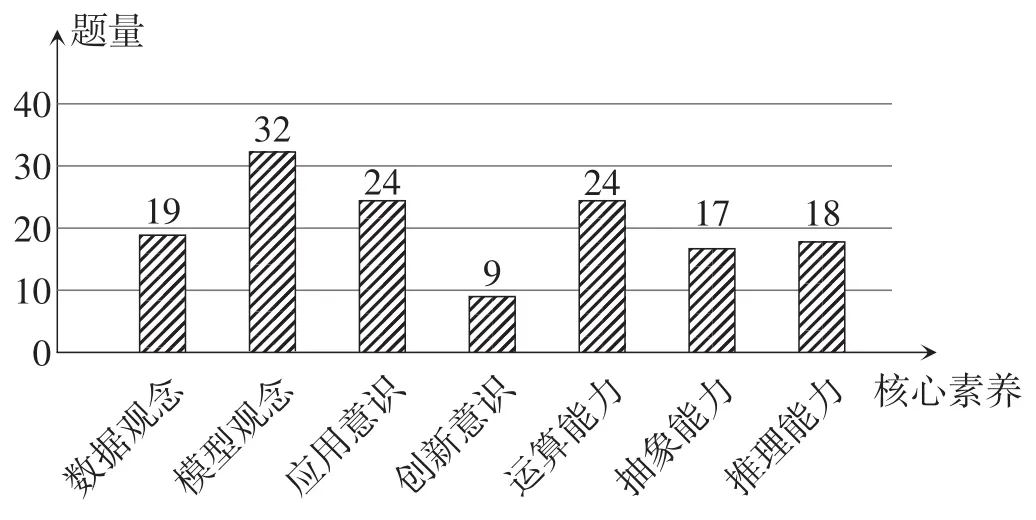
图1

二、命题特点分析

1.全面考查基础知识，突出对核心概念的理解

随机事件的概念是认识随机事件概率的基础，以实际生活中常见的随机现象为情境素材，设置判断必然事件、随机事件、不可能事件的问题是中考相关试题的一般性命题思路.随机事件概率的意义一般从随机事件在每次试验中是否发生，以及发生的可能性大小的角度来考查.

例1（湖北·武汉卷）彩民李大叔购买1张彩票，中奖.这个事件是（ ）.

（A）必然事件 （B）确定性事件

（C）不可能事件 （D）随机事件

答案：D.

考查目标：随机事件、必然事件、不可能事件的概念.

命题意图：此题主要考查学生对随机事件、必然事件、不可能事件概念的掌握情况.在解决问题的过程中，侧重引导学生意识到数学情境来源于现实生活，着重考查学生的数据观念和应用意识.

命题评价：此题属于基础题.通过对随机事件、必然事件、不可能事件概念的考查，引导教师在教学活动中注重通过多列举生活中常见的随机现象来引导学生理解核心概念的意义，从而强化学生对基础知识的掌握.

例2（湖北·襄阳卷）下列说法正确的是（ ）.

（A）自然现象中，“太阳东方升起”是必然事件

（B）成语“水中捞月”所描述的事件，是随机事件

（C）“襄阳明天降雨的概率为0.6”，表示襄阳明天一定降雨

答案：A.

考查目标：事件的概率和事件发生的随机性之间的关系.

命题意图：通过“太阳东方升起”“水中捞月”“降雨的概率”“抽奖活动的概率”等生活实例考查学生对概率意义的理解，考查学生对事件的概率和事件发生的随机性之间关系的掌握情况.在解决此类问题的过程中，需要运用到大量的生活常识和跨学科知识，着重考查了学生的应用意识和创新意识.

命题评价：此题属于基础题.在引导学生辨析事件的概率和事件发生的随机性之间的关系的同时，教师要引导学生应用数据观念去分析生活常识及跨学科事例.

例3（贵州·贵阳卷）某校九年级选出三名同学参加学校组织的“法治和安全知识竞赛”.比赛规定，以抽签方式决定每个人的出场顺序.主持人将表示出场顺序的数字1，2，3分别写在3张同样的纸条上，并将这些纸条放在一个不透明的盒子中，搅匀后从中任意抽出一张，小星第一个抽，下列说法中正确的是（ ）.

（A）小星抽到数字1的可能性最小

（B）小星抽到数字2的可能性最大

（C）小星抽到数字3的可能性最大

（D）小星抽到每个数的可能性相同

答案：D.

考查目标：基本事件发生的可能性大小.

命题意图：此题以抽签活动为背景，考查基本事件发生的可能性大小，考查学生在学习过程中获得数学基本活动经验的情况，以及是否具备了应用意识，是否能用数学的眼光观察现实世界.

命题评价：此题属于基础题.概率试题的问题情境都是生活中常见的随机现象，且大部分情境在教材中都有所呈现，一般通过选择题或填空题的形式进行考查.通过对基本事件发生的可能性大小的考查，引导教师在教学活动中要注重学生基本活动经验的获得，并培养学生的“数学眼光”.

2.重点考查数学方法，突出模型观念

（1）古典概型.

用列举法求随机事件的概率是定量研究随机现象的重要内容.通常以摸球、抛硬币、抽扑克牌等学生熟悉的随机试验为载体，通过画树状图或列表呈现出基本事件及所求随机事件的结果，用古典概型公式求解.从2022年中考“随机事件的概率”部分的试题来看，在考查基本模型的基础上，命题背景的设计更加新颖，突出考查了学生的建模思想和化归思想.

例4（北京卷）不透明的袋子中装有红、绿小球各一个，除颜色外两个小球无其他差别.从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么第一次摸到红球、第二次摸到绿球的概率是（ ）.

答案：A.

考查目标：古典概型——摸球模型.

命题意图：让学生在列出所有等可能出现的结果（红，红），（红，绿），（绿，红），（绿，绿）后，根据结果（红，绿）出现的次数，再利用概率公式进行计算.此题考查学生用画树状图法或列表法解决两步试验的概率问题的同时，考查学生区别两步试验中的“放回”和“不放回”模型的能力，以及学生的模型观念和运算能力.

命题评价：此题属于基础题.此类问题属于概率部分的重点问题，在中考试题中经常出现.在教学中，教师要引导学生经历“建模—识模—用模”的过程，注重让学生在过程中获得数学经验、提升模型观念.

例5（山东·济南卷）某班级计划举办手抄报展览，确定了“5G时代”“北斗卫星”“高铁速度”三个主题，若小明和小亮每人随机选择其中一个主题，则他们恰好选择同一个主题的概率是（ ）.

答案：C.

例6（江西卷）某医院计划选派护士支援某地的防疫工作，甲、乙、丙、丁4名护士积极报名参加，其中甲是共青团员，其余3人均是共产党员.医院决定用随机抽取的方式确定人选.

（1）略；

（2）若需要从这4名护士中随机抽取2人，试用画树状图法或列表法求出被抽到的两名护士都是共产党员的概率.

考查目标：可以化归为摸球模型的古典概型.

命题意图：例5和例6可以化归为摸球模型，考查了学生识模、用模的能力.注重考查学生正确识别，并利用树状图或列表表示“放回”模型和“不放回”模型的能力.在解决问题的过程中，学生应该具备模型观念和应用意识.

命题评价：例5属于基础题，例6属于中档题.两道试题都突出了数学在实际生活中的应用价值.通过画树状图法或列表法求概率依然是今后中考考查的重点内容，命题设计更加重视试题情境的随机性和等可能性，注重基本模型的抽象，考查学生的转化思想、抽象能力和模型观念.采用解答题的形式考查此部分内容，能够呈现出随机试验的基本事件结果和随机事件结果，充分体现《标准》的要求.复习中，教师要引领学生基于核心要素，剥去“背景”的外衣，抓住数学内容的本质；教学中，教师要注重培养学生的模型观念，注重让学生经历获得数学经验的过程.

例7（辽宁·阜新卷）如图2，是由12个全等的等边三角形组成的图案，假设可以随机在图中取点，那么这个点取在阴影部分的概率是（ ）.

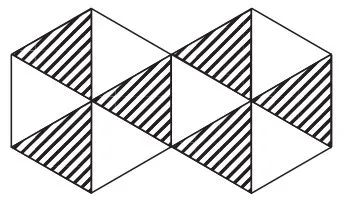
图2

答案：D.

考查目标：几何概型.

命题意图：此题考查学生对几何概型和古典概型的共同点是随机事件发生的等可能性，以及几何概型中随机事件发生的可能结果的无限性的认识情况.

命题评价：此题属于基础题.命制试题时，常常用线段长度、图形面积、几何体体积作为基本事件和随机事件的结果数，再利用概率公式计算.《标准》对此部分内容要求不高，各版本的教材对这部分内容的处理也不一样，这就要求教师在复习教学中应该注意题目不宜过难，要将教学重点放在将其转化为古典概型上，以加深学生对随机事件的概率的理解.

（2）用频率估计概率.

刻画随机事件概率的方法有两种：古典概型公式和用频率估计概率.用频率估计概率更具有一般性.《标准》对此部分内容的要求是：知道通过大量重复试验，可以用频率估计概率.此类试题一般给出试验的数据，通过数据估计概率，考查的目的是求概率不能停留在对古典概型的训练上，而应该培养学生的一般观念，即随机思想.渗透随机思想是把握“可能性”的重点，引导教师在教学中强调让学生经历试验活动，在试验活动中积累活动经验，培养数据观念.

例8（甘肃·兰州卷）2022年3月12日是我国第44个植树节，某林业部门为了考察某种幼树在一定条件下的移植成活率，在同等条件下，对这种幼树进行大量移植，并统计成活情况，表2是这种幼树移植过程中的一组统计数据.

表2

估计该种幼树在此条件下移植成活的概率是____.（结果精确到0.1.）

答案：0.9.

考查目标：通过大量重复试验，用频率估计概率.

命题意图：学生对用概率刻画随机事件发生可能性的大小有了一定的体会，但是对其反映的随机性的内涵认识不足，容易停留在“比值”层面.此题考查学生对在大量重复试验的过程中频率所呈现出的稳定性和规律性、频率与概率之间的关系，以及利用频率估计概率的掌握程度.

命题评价：此题属于基础题.在教学中，教师要引导学生经历大量重复试验的过程，让学生在过程中体会频率所呈现出的稳定性和规律性，进而认识到频率与概率之间的关系，并进一步运用频率估计概率.

3.加强应用性，体现试题情境的育人价值

《标准》要求命题要突出知识的应用性，考查学生分析问题和解决问题的能力.数学教育承载着立德树人的根本任务，不仅体现在课堂教学中，也体现在考查目标里.以数学文化为素材的概率试题逐渐成为中考试卷的一个亮点.

例9（内蒙古·包头卷）2022年2月20日北京冬奥会大幕落下，中国队在冰上、雪上项目中，共斩获9金4银2铜，创造了中国队冬奥会历史最好成绩.某校为普及冬奥知识，开展了校内冬奥知识竞赛活动，并评出一等奖3人.现欲从小明等3名一等奖获得者中任选2名参加全市冬奥知识竞赛，则小明被选到的概率为（ ）.

答案：D.

例10（山西卷）“二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界誉为“中国第五大发明”.小文购买了“二十四节气”主题邮票，他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小文将它们背面朝上放在桌面上（邮票背面完全相同），如图3，让小乐从中随机抽取一张（不放回），再从中随机抽取一张，则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是（ ）.

图3

答案：C.

考查目标：德育背景下的古典概型.

命题意图：通过可以转化为摸球模型的概率问题，考查学生的模型观念和应用意识.与此同时，例9以冬奥会为背景，通过介绍我国体育事业的发展来树立学生的民族自信；例10以“二十四节气”为背景，彰显我国优秀传统文化的博大精深，树立学生的文化自信.

命题评价：例9和例10都属于基础题.试题情境已经成为评价试题的重要维度.2022年中考“随机事件的概率”相关试题，特别突出应用性，在情境设置上更加丰富，选取了与日常生活、环保健康、传统文化、民俗风情、社会热点问题相关的情境，将社会主义核心价值观和优秀传统文化融入试题中，充分发挥了中考试题的育人功能.教学中，教师应该注重教学情境的设置，以充分发挥数学学科的育人价值与作用.

例11（江苏·盐城卷）如图4，电路图上有A，B，C共3个开关和1个小灯泡，闭合开关C或同时闭合开关A，B都可以使小灯泡发亮.任意闭合其中的1个开关，小灯泡发亮的概率是________.

图4

例12（四川·南充卷）老师为帮助学生正确理解物理变化与化学变化，将6种生活现象制成看上去无差别卡片（如图5）.从中随机抽取一张卡片，抽中生活现象是物理变化的概率是________.

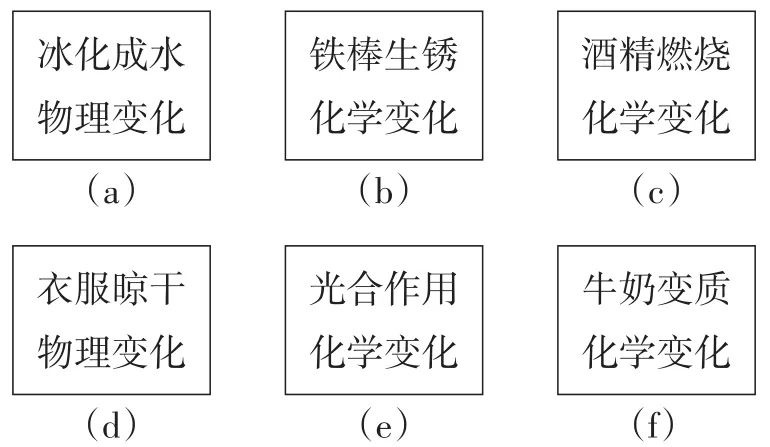
图5

考查目标：求解以跨学科情境为背景的概率问题.

命题意图：通过以跨学科情境为背景命制的概率试题，考查学生运用跨学科知识解决问题的能力.例11以物理学中的电路图为背景命制；例12以化学中的物理变化和化学变化为背景命制，考查学生综合运用数学和其他学科知识与方法解决问题的能力，考查学生的应用意识和创新意识.

命题评价：例11和例12都属于中档题.2022年中考“随机事件的概率”相关试题不仅关注了学生情感、态度和价值观的发展，还设置了跨学科的情境问题，这是中考改革的一个重要方向.数学与物理、化学、生物等学科联系密切，在学科交会处命制试题有较多的素材可选择.教学中，教师要注重引导学生体会不同情境中蕴含的数学问题.

4.注重知识的综合性，体现核心素养导向的考查

2022年中考“随机事件的概率”试题的综合性有所提升.通过知识的交叉、渗透和组合来考查数学知识之间、数学与其他学科之间、数学与生活之间的联系，考查相关知识与方法、能力与素养.

例13（广东·深圳卷）某工厂进行厂长选拔，从中抽出一部分人进行筛选，其中有“优秀”“良好”“合格”“不合格”.

（1）本次抽查总人数为_______，“合格”人数的百分比为_______；

（2）补全如图6所示的条形统计图；

图6

（3）如图7，扇形统计图中“不合格”人数的度数为_______；

图7

（4）在“优秀”中有甲、乙、丙三人，现从中抽出两人，则刚好抽中甲乙两人的概率为_______.

答案：（1）50人，40%；（2）略；（3）115.2°；（4）

考查目标：同领域主题间的概率问题.

命题意图：此题考查学生对条形统计图和扇形统计图，以及频数和样本概念的理解.同时，全面考查学生的数据观念、模型观念、运算能力和应用意识.

命题评价：此题属于中档题.同领域主题间的知识综合是中考命题的一种趋势.教学中，教师要注重知识上的融合，并逐步在知识的内在联系与融合上实现创新.

例14（广西·玉林卷）问题情境：在数学探究活动中，教师给出了如图8所示的图形及下面三个等式：①AB=AC；②DB=DC；③∠BAD=∠CAD.若以其中两个等式作为已知条件，能否得到余下一个等式成立？

图8

解决方案：探究△ABD与△ACD全等.

问题解决：

（1）当选择①②作为已知条件时，△ABD与△ACD全等吗？_________（填“全等”或“不全等”），理由是________；

（2）当任意选择两个等式作为已知条件时，试用画树状图法或列表法求△ABD≌△ACD的概率.

例15（江苏·常州卷）在5张相同的小纸条上，分别写有语句：①函数表达式为y=x；②函数表达式为y=x2；③函数的图象关于原点对称；④函数的图象关于y轴对称；⑤函数值y随自变量x增大而增大.将这5张小纸条做成5支签，①②放在不透明的盒子A中搅匀，③④⑤放在不透明的盒子B中搅匀.

（1）从盒子A中任意抽出1支签，抽到①的概率是__________；

（2）先从盒子A中任意抽出1支签，再从盒子B中任意抽出1支签.求抽到的2张小纸条上的语句对函数的描述相符合的概率.

考查目标：随机事件的概率与图形的性质、函数的图象及性质等知识的综合.

命题意图：例14和例15分别是对随机事件的概率与图形的性质、函数的图象及性质相结合的跨领域内容的考查，设计新颖、难度适中，通过画树状图或列表解决问题.试题实现了跨领域内容的考查，是对学生数学核心素养的综合考查.

命题评价：例14和例15都属于中档题，都是跨领域主题的综合试题，具有一定的难度.教学中，教师要注重培养学生的综合能力，注重培养学生灵活运用数学基本活动经验和基本思想解决问题的能力，注重培养学生的应用意识和创新意识，从而让学生在解决问题时能做到举一反三、触类旁通.

三、复习教学建议

1.立足“四基”“四能”，坚持“依标定教”

结合上文的分析，笔者认为2023年中考“随机事件的概率”试题的命制仍然会保持稳定中有所创新，坚持考查“四基”“四能”，试题以简单题和中等难度题为主，内容主要涉及随机事件的概念、随机事件概率的意义、用画树状图法或列表法求概率和用频率估计概率.复习教学中，教师要认真研读《标准》，进一步明确《标准》对随机事件的概率的学习要求和质量评价标准，准确把握复习内容的深度、广度和难度，不随意超标或提高难度.例如，对于随机事件概念的复习，由于它是从小学阶段的定性描述逐步转向初中阶段的定量分析，故应该通过设置简单易懂的情境，引导学生感悟随机事件.复习教学中，教师要选择生活中常见的随机现象加深学生对随机事件概念的理解，不要以过多的数学知识为背景，避免削弱学生对随机事件概念的理解.在利用画树状图法或列表法求随机事件的概率时，建议以两步试验为主，不要涉及三步及以上的随机试验问题，以免加大学生求解概率的计算量.教材是教学的主要载体，立足基础就要回归教材，挖掘和改编教材例题和习题，充分发挥教材例题和习题的功能.

2.突出思想方法，坚持素养立意

《标准》要求在教学设计和实施时要坚持素养导向，充分关注核心素养在教学中的达成情况.因此，复习教学更要指向学生核心素养的发展.“随机事件的概率”内容中蕴含着随机思想、转化与化归思想、分类讨论思想、模型思想等丰富的数学思想.在没有学习排列组合知识的情况下，画树状图和列表是解决古典概型计算问题的重要方法.在复习教学中，一方面，可以让学生画思维导图或鱼骨图建立知识结构，明确知识之间的内在联系，感悟数学本质和基本思想；另一方面，可以围绕基本模型，通过对具有典型性、拓展性和探究性的变式题的练习，将其内化为学生的认知结构，从而培养学生的数据观念、模型观念、抽象能力、运算能力等素养.

3.注重综合应用，坚持育人导向

《标准》指出，要适当提高应用性、探究性和综合性试题的比例，题目设置要注重创设真实情境.因此，2023年中考“随机事件的概率”试题仍然会密切结合生活实际和社会热点进行命制.复习教学中，教师要重点选择统计与概率综合的题目，并兼顾与其他领域知识联系的综合性题目，以及从不同角度考查学生的思维能力、体现数学内涵和价值的题目.同时，还要关注情境的教育性，注意挖掘能激发学生爱国情怀、弘扬数学文化的素材，真正实现复习教学激发兴趣、培养习惯、立德树人的目标.

四、典型模拟题

1.如图9，湖边建有A，B，C，D共4座凉亭，某同学计划将这4座凉亭全部参观一遍，从入口处进，先经过凉亭A，接下来参观凉亭B或凉亭C（已经参观过的凉亭，再次经过时不作停留），则最后一次参观的为凉亭D的概率为（ ）.

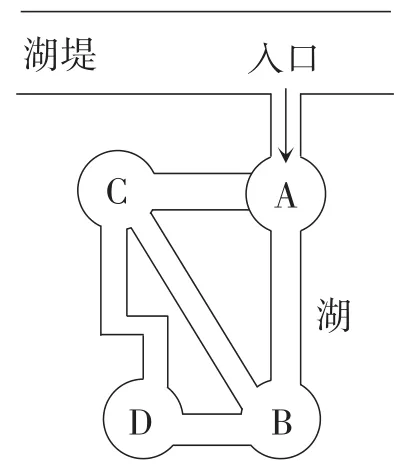
图9

答案：C.

2.如图10，有4张反面无差别的卡片，其正面分别印有国际数学家大会的会标，现将4张卡片正面朝下放置，混合均匀后从中随机抽取2张，则抽到的卡片正面图案都是中心对称图形的概率为（ ）.

图10

答案：C.

3.林业部门要考查某种树苗在一定条件下的移植成活率，表3是这种树苗在移植过程中的一组统计数据.估计该种树苗在此条件下移植成活的概率为_______.（结果精确到0.01.）

表3

答案：0.88.

4.中华文化源远流长，在文学方面，《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表，被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况，就“你读完了几部四大古典名著”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如图11和图12所示的两个不完整的统计图，试结合图中信息解决下列问题.

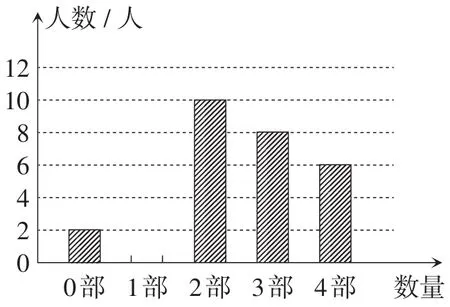
图11

图12

（1）本次调查一共抽取了_______名学生；扇形统计图中“1部”所在扇形的圆心角的度数为_______；

（2）被抽取学生阅读四大名著的平均本数为_____；

（3）若该中学有1 000名学生，试估计至少阅读3部四大古典名著的学生有多少？

（4）没有读过四大名著的2名学生准备从四大古典名著中各自随机选择一部来阅读，求他们选中同一名著的概率.

答案：（1）40，126°；（2）2.05；（3）350名；（4）