面向软件定义车联网的链路故障快速恢复方法

顾源，张震，段通

（1.战略支援部队信息工程大学 信息技术研究所，郑州 450002；2.国家数字交换系统工程技术研究中心，郑州 450002）

0 引言

车联网（Internet of Vehicles，IoV）是智能交通系统的重要组成部分，通过车联网与路侧基础设施进行信息交换，可为车辆提供辅助驾驶、异常提醒、躲避拥堵等多种服务信息；但紧耦合的网络设备操作方式以及对可扩展性、灵活性、可靠性需求的增长导致传统车联网难以满足未来网络的发展需求［1］。软件定义网络（Software Defined Network，SDN）作为一种新型网络结构，通过三层架构实现了控制平面与数据平面的分离［2］，并由控制平面的控制器实现网络控制［3］，满足了车辆的连通性和通信需求［4］，同时具有加入蜂窝网络和车联网的潜力［5］。软件定义车联网（Software-Defined Internet of Vehicles，SDIV）架构［6］支持车联网开放统一的接口，数据层与控制层的分开和逻辑上的集中控制使SDIV 架构具有很高的可扩展性和网络可管理性，如图1 所示。

图1 SDIV的三层架构Fig.1 Three-layer architecture of SDIV

图2 中的车路协同通信是车联网中一种典型的实时查询类通信场景，在这种场景下车联网需与路侧基础设施进行V2I（Vehicle to Infrastructure）通信，从路侧的信息服务器（Information Server，IS）中获取实时道路导航、充电设施位置、交通拥堵等信息。路侧单元（RoadSide Unit，RSU）通过无线信道与车联网相连，同时通过路由器与IS 相连，从而将车联网所请求的数据信息从IS 发送至车联网。在SDIV 架构中，RSU 和IS 之间的路由器均为SDN 交换机，而从IS 到RSU 之间的数据流量传输路径也被SDN 控制器所控制，因此具有较高的灵活性。然而，当RSU 与IS 之间的通信系统发生链路故障时，SDN 控制器需要根据实时网络状态更新交换机的流表规则，以快速恢复传输。同时，此类场景中车辆的快速移动特性以及所连RSU 潜在的切换特性需要快速的故障恢复能力，以保持车联网的服务质量，最终满足用户需求。

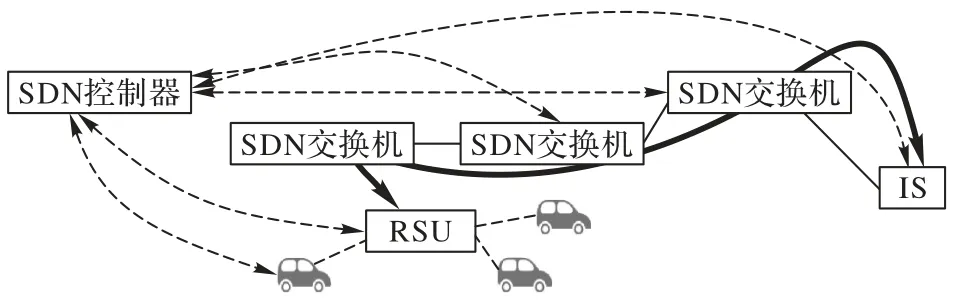
图2 实时查询类通信场景Fig.2 Real-time query communication scenario

对于链路故障恢复问题，文献［7-10］中提前安装了备份路径的转发规则。当链路出现故障时，数据平面交换机自动激活备份路径，在提前配置备份路径的转发规则方案中，不涉及SDN 控制器，因此能够快速地从链路故障中恢复。但工作路径和备份路径相关，每次改变工作路径时，都需要重新分配备份路径，因此容易导致交换机和链路带宽资源耗尽，并不适用于车联网场景中复杂且动态变化的网络环境。

文献［11］中提出了一种基于最短路径优先算法的响应式链路故障恢复方法。该方法将每条路径上的报文分为高优先级和低优先级，保证了高优先级数据包的最小延迟，还通过在可用路径上平均分配流量以避免拥塞。因此，随着网络规模的扩大，该方法的复杂度也随之增加。该方法的另一个缺点是为实现机制提供的信息不足；此外，还没有在标准的互联网拓扑数据集上进行测试。文献［12］中表示忽略流表处理时间的基于最短路径恢复可能无法快速恢复流表时延。

根据文献［13-14］的研究，SDN 交换机中插入一条流表的延迟为0.5～10 ms。文献［15-16］中关注了恢复过程中的流表处理时间，考虑了异构网络中节点具有不同规格的路径交换延迟问题，并基于处理时间最短的交换机选择备选路径。文献［17］中提出一种考虑恢复过程中的交换机流表处理时间和网络带宽的方法。文献［18］中提出基于社区检测的方法和基于路径解剖的方法。文献［19］中在替代路径选择时，鼓励选择具有更好的链路质量和最小的关键交换机数量的路径。文献［15-19］考虑了流表更新时延，但没有综合考虑路径开销和流表更新权衡问题，其中文献［15-17］从降低每个交换机处理时间的角度，降低恢复时延；文献［18-19］从减少路径恢复过程中流表更新数量的角度，降低恢复时延。文献［20］中考虑了路径开销和流表更新权衡问题，并在一定条件下找到最优解和次优解，但没有将路径开销和流表更新次数统一为时间标准后进行权衡，并且只能在系数特定的情况下求解。

基于以上研究现状，为解决软件定义车联网实时查询类通信场景中的单链路障恢复问题，本文引入恢复过程时延和恢复之后路径传输时延作为链路参数，并设计相应的路径恢复方案。本文的主要工作有：1）对故障恢复时延建模，综合考虑恢复过程时延和恢复之后路径开销这两个关键性能指标：2）在流表更新时延可以忽略和流表更新时延不可忽略的情况下，分别提出两种路径恢复算法，理论分析和实验结果表明，本文算法具有较小的计算时延和故障恢复时延。

1 问题描述与模型构建

1.1 问题描述

SDIV 架构下链路故障恢复机制的优劣主要由以下性能指标评估：1）恢复过程的时延开销trecovery，由故障发现时延tdiscovery、openflow 消息通道时延topenflow（包括packet-in 消息上传及packet-out 消息的下发等）、路径计算时延tcompute和流表更新时延tupdate构成。其中：tdiscovery和topenflow由通信系统本身的性能决定，无法优化；tupdate则由旧路径切换到新路径所需要的流表规则增删操作次数决定。2）恢复之后的路径传输时延tnewpath，一般由路径的端到端时延所定义，以实现最小的新路径传输时延。因此在求解链路故障恢复问题时，tcompute、tupdate、tnewpath可以优化，且tupdate和tnewpath可以参数化。本文首先将tupdate和tnewpath参数化，并统一到链路故障恢复的优化目标中；其次，在求解优化问题的过程中，在最小化tupdate和tnewpath的同时考虑tcompute，寻找统筹上述关键性能指标的最优解。

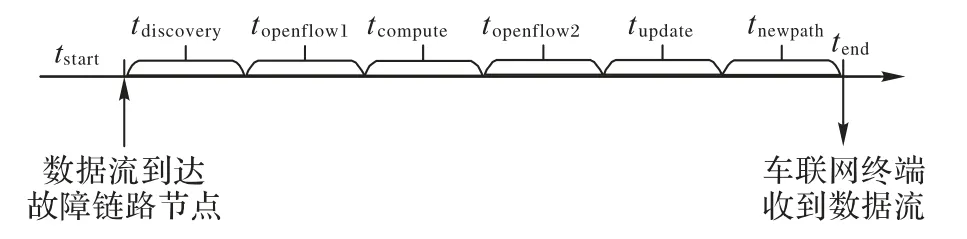
图3 SDIV架构下链路故障恢复机制时延Fig.3 Delay of link faulure recovery mechanism under SDIV architecture

1.2 模型构建

网络拓扑结构表示为G=(V，E)，其中：V={vi}表示拓扑中的节点集合，vs为路径上的源节点，vt为路径上的目的节点；E={ei，j}表示拓扑中的链路集合，ei，j表示节点vi和vj之间的边，efailure表示故障链路。Pold={xi，j}定义为拓扑中一系列连续节点组成的旧路径，本文假设该路径为一条不包含环路的简单路径，每个xi，j为该路径中相邻节点vi、vj组成的一段链路，其中：xi，j=1 表示路径经过ei，j；xi，j=0 表示路径不经过ei，j。对恢复传输后的新路径定义为Pnew={yi，j}，假设该路径为一条不包含环路的简单路径，每个yi，j为该路径中相邻节点vi、vj组成的一段链路，其中：yi，j=1 表示路径经过ei，j；yi，j=0 表示路 径不经过ei，j。用{ci，j}表示链 路传输时延，新路径Pnew={yi，j}的路径传输时延为

图4 是一个含有7 个节点的拓扑，除c2，7=c7，4=2 外，剩余边的链路传输时延均为1。如果原传输路径为P1：1-2-3-4，在链路e2，3发生故障时，需要重新选择路径恢复传输，备选路径有P2：1-2-5-6-4 和P3：1-2-7-4。P2 和P3 的路径传输时延可以由计算得出，分别是4 和5。

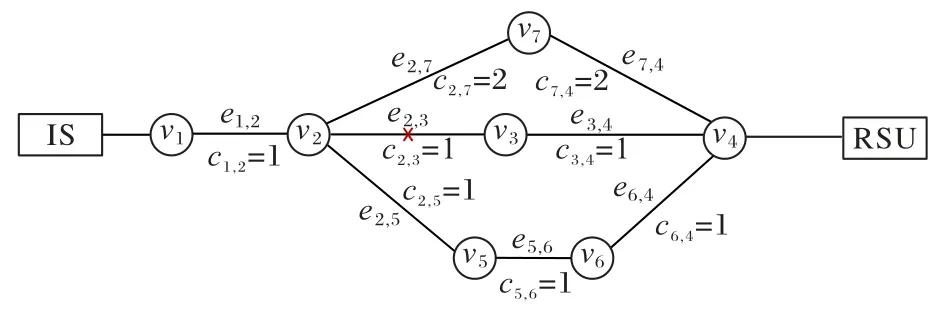
图4 SDIV架构下链路故障恢复示例Fig.4 Example of link failure recovery under SDIV architecture

路径Pold上存在一段故障链路efailure。由于tdiscovery、topenflow均由通信系统本身性能决定，无法优化，对于trecovery，主要考虑tupdate。在路径切换时，相应的SDN 交换机需要在流表中增添或删除流条目，此类操作的总数是流表规则更新次数。tupdate由旧路径Pold切换到新路径Pnew所需要的流表规则更新次数决定。

其中：xi，j表示去掉故障链路efailure后，旧路径中包含的边数量；wi，jyi，j表示去掉故障链路efailure后，新路径中的每个边如果与旧路径中的边相同就减1，如果与旧路径中的边不相同则加1，相当于对两条路径上不同边的数量进行统计。

由于式（1）中第1 项由旧路径中包含链路的数量决定，在备选新路径比较中固定不变，在求解优化问题过程中可将xi，j项去掉，有：

tupdate为更新次数与每次更新所需时间乘积，用tope表示一次流表更新的时间开销，tupdate可表示为：

图4 中拓扑原传输路径为P1：1-2-3-4，在链路e2，3发生故障时，需要重新选择路径恢复传输，备选路径有P2：1-2-5-6-4 和P3：1-2-7-4。如果选择P2，需要将经过e2，5、e4，6、e6，4的流表条目添加到对应节点的流表中，此外还要删除穿过e3，4的流表对应条目，因此需要4 次流表更新，由式（1）也可算出P2 的流表规则操作次数Cope_nonop=4，在后续优化问题过程中，按式（2）将xi，j项去掉后Cope=2。如果选择P3，则需将经过e2，7、e7，4的流表条目分别添加到节点v2和v7的流表中，并且删除节点v3中e3，4对应的流表条目，因此需要3 次流表操作，去掉xi，j项后Cope=1。因此P2 的流表更新时延为tupdate=2tope，P3 的流表更新时延为tupdate=tope。

在SDIV 链路故障恢复求解过程中，要找到一条总时延开销最低的路径，需要满足min(tupdate+tnewpath)。新路径Pnew={yi，j}应为一条没有环路的简单路径，并且需要满足流表的连通性或守恒条件，即：

其中：bi是拓扑中从节点vi的流出，表征流存在状态。对于从源节点vs到目的节点vt之间的流，有：

综上，为统筹恢复过程的时延开销和恢复之后的路径时延开销，本文将SDIV 链路故障恢复问题（SDIV Link Fault Recovery Problem，SLFRP）描述如下：

图4 拓扑在原传输路径P1：1-2-3-4 中链路e2，3发生故障的情况下，备选路径P2 的时延开销为tP2=tupdate+tnewpath=4+2tope，备选路径P3 的时延开销为tP3=tupdate+tnewpath=5 +tope，对于该拓扑，只需比较tP2和tP3，选择总时延最小的路径作为新路径即可。

2 故障快速恢复算法

由式（6）可以看出，SLFRP 本质上是在边权值为wi，jtope+ci，j的新拓扑中求解最短路径，可通过Dijkstra 算法等最短路径算法求解。然而，重新运行Dijkstra 算法计算最短路径的复杂度O(N2)偏高，会导致tcompute过大。由于边权值的改变，先前构建的原始最短路径的计算结果又似乎难以复用。为此，本文分析SLFRP 和先前构建的原始最短路径之间的联系，力图最大化复用已有计算结果，提出基于拓扑划分的路径恢复算法（Path Recovery Algorithm based on Topology Partition，PRA-TP）和基于单链路搜索的路径恢复算法（Path Recovery Algorithm based on Single Link Search，PRA-SLS）：在流表更新时延tupdate相较于tnewpath不可被忽略的情况下，PRATP 复用链路故障产生的两个子树节点集合，降低了计算复杂度；在流表更新时延tupdate可被忽略时，PRA-SLS 复用链路故障产生的两个子树路径集合，降低了计算复杂度。

2.1 基于拓扑划分的路径恢复算法

对于流表更新时延tupdate相较于tnewpath不可被忽略情况下的SLFRP，故障链路中断后，拓扑链路权值为wi，jtope+ci，j，与原权值相比发生变化。对于这种情况，PRA-TP 通过复用故障链路划分的原最短路径生成树的两个子树中节点集合求解问题。在链路故障恢复场景中，当以vs和vt为源点和目的点的路径Pold={xi，j}中的某条链路发生故障时，需要找到一条以vs和vt为源点和目的点的新路径Pnew={yi，j}。Told为链路故障前以源点vs为根节点的原最短路径生成树，Pold在Told上，表示源点vs到目的节点vt的原最短路径，Pnew表示恢复传输后的新最短路径。在Pold中选择某链路efailure作为故障链路，将故障链路efailure从Told中移除，Told被分割成两个子树Told_s和Told_t，分别包含源点vs和目的点vt。假设vi为Told_s中的某节点，vj为Told_t中的某节点。ei，j为一条链路，头节点为vi，尾节点为vj，且ei，j∈Eefailure，满足上述条件的所有ei，j的集合表示为L，即：

用dis_to_vs(i)表示vs到vi的距离，distance(i，j)表示边ei，j的距离，dis_to_vt(j)表示vj到vt的距离。当且仅 当dis_to_vs(i)、Cost(i，j)、dis_to_vt(j)之和最小的时候链路ei，j在最短路径上，即ei，j∈Pnew当且仅当：

当故障链路efailure从Told中移除时，点集V={vi}被分割成点集Vs和点集Vt，其中Vs包含Told_s中全部节点，Vt包含Told_t中全部节点，显然vs∈Vs，vt∈Vt。对于Vs中任意节点vi，存在一条vi到vs的最短路径，该路径中不包含Vt中节点；对于Vt中任意节点vj，也存在一条vj到vt的最短路径，该路径中不包含Vs中节点。在计算Pnew时，对原拓扑G=(V，E)删除故障链路，只保留点集Vs中的节点和首尾节点均在点集Vs中的链路，得到拓扑Gs=(Vs，Es)，对Gs以vs为根节点生成最短路径树Tnew_s，而后对原拓扑G=(V，E)删除故障链路，只保留首尾节点均在Vt中的链路和节点，得到Gt=(Vt，Et)，并以vt为根节点生成最短路径树Tnew_t，再遍历L中所有ei，j，计 算dis_to_vs(i)、Cost(i，j)、dis_to_vt(j)之和并比较结果，最小的值即为新最短路径。

图4 拓扑中，v1为源点vs，v4为目的点vt，原传输路径Pold：1-2-3-4，故障链路为e2，3，原最短路径生成树Told以及被故障链路划分的子树Told_s和Told_t如图5（a）所示。点集Vs={v1，v2，v5，v6，v7}，点集Vt={v3，v4}，集合L={e6，4，e7，4}。在原拓扑中只保留首尾节点均在Vs中的链路，拓扑中剩余点为点集Vs，剩余边为{e1，2，e2，5，e5，6，e2，7}，生成最短路径树Tnew_s。在原拓扑中只保留首尾节点均在Vt中的链路，拓扑中剩余点为点集Vt，剩余边为{e3，4}，对其生成最短路径树Tnew_t，Tnew_s和Tnew_t如图5（b）所示，而后遍历集合L={e6，4，e7，4}中ei，j，其中：e6，4的时延 为dis_to_vs(6)+distance(6，4)+dis_to_vt(4)=4+2tope，e7，4的时延为dis_to_vs(7)+distance(7，4) +dis_to_vt(4)=5 +tope，二者中更小的即为最短路径。

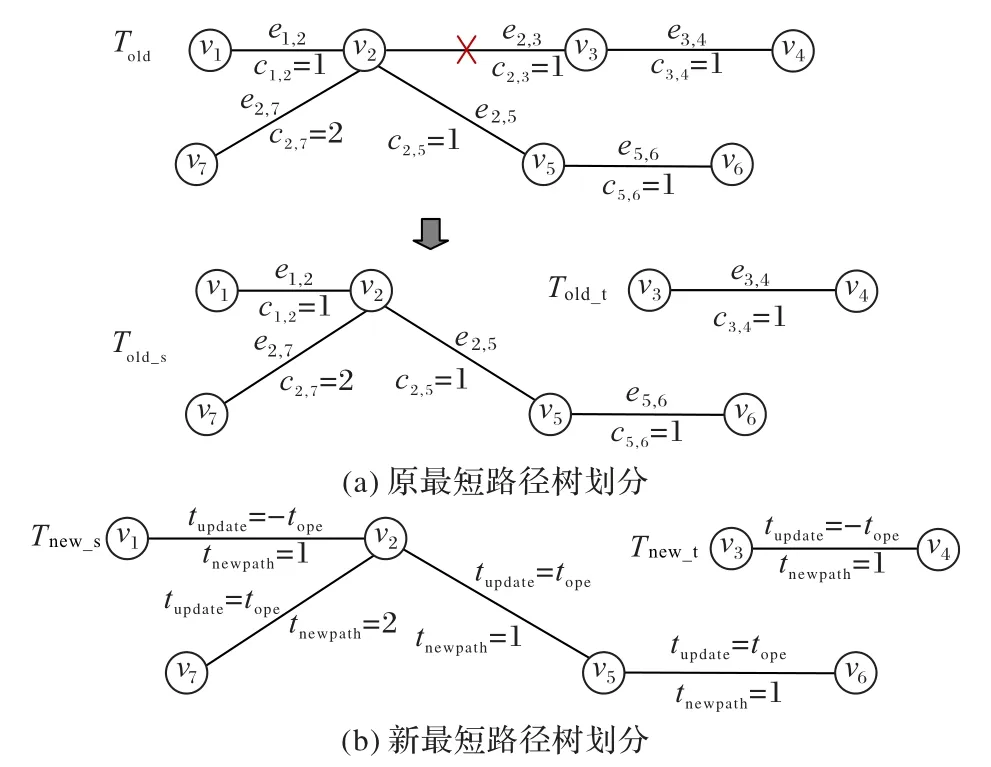
图5 最短路径树划分Fig.5 Shortest path tree partition

为便于描述算法，定义如下操作。

Cost(G)：计算拓扑G中链路权重。

Divide(Told，efailure，Told_s，Told_t)：将故障链路efailure从Told移除后，分割出两个子树，包含源点vs的子树为Told_s，包含目的点vt的子树为Told_t。

Distance(T，i)：找到最短路径生成树T上，点vi到根节点的距离。

Path(T，i)：返回最短路径生成树T上，点vi到根节点的路径。

CpyNodes(V，G)：拓扑G中所有的点复制到V中。

Relax(i，Cost(ei，j)，j)：遍历L中的ei，j，找到使Distance(Tnew_s，i)、Cost(ei，j)、Distance(Tnew_t，j)之和最 小的i和j。

2.2 基于单链路搜索的路径恢复算法

对于流表更新时延远小于路径传输时延情况下的SDIV链路故障恢复问题，PRA-SLS 通过复用故障链路划分产生的两个子树的路径集合求解问题。对忽略流表更新时延的SLFRP 可以描述如下：

由于忽略流表更新时延tope，拓扑Gs=(Vs，Es)上的链路参数与原拓扑G=(V，E)相比没有发生变化，拓扑Gs上的最短路径生成树也没有变化，Tnew_s可以直接由原最短路径树得出，即Tnew_s=Told_s。对Gt=(Vt，Et)，以vt为根节点生成最短路径树Tnew_t，而后遍历L中所有ei，j，计 算dis_to_vs(i) +Cost(i，j)+dis_to_vt(j)结果并比较，其中值最小的即为新的最短路径。

2.3 算法时间复杂度分析

假设拓扑G中去掉故障链路后有N条链路，用故障链路划分拓扑和原最短路径树后，Gt中有M条链路，集合L中有K条链路。PRA-TP 中步骤的时间开销主要有：1）遍历拓扑G划分Gs、Gt和集合L，时间复杂度为O(N)；2）Dijkstra(Gs)的时间复杂度为O((N-M-K)2)；3）Dijkstra(Gt)的时间复杂度为O(M2)；4）遍历集合L的时间复杂度为O(K)，PRA-TP 的时间复杂度为O((N-M-K)2+M2)，略小于Dijkstra 算法，当Gs和Gt中链路数量相同时，时间开销最小。PRA-SLS 时间开销主要有：1）遍历拓扑G，划分Gs、Gt和集合L，时间复杂度为O(N)；2）Dijkstra (Gt)的时间复杂度为O(M2)；3）遍历集合L的时间复杂度为O(K)。PRA-SLS 时间复杂度为O(M2)。

3 实验与结果分析

通过比较算法计算时延和路径恢复时延，评估路径恢复方案。选取SNDlib［21］和topology zoo［22］中的不同拓扑进行实验，拓扑结构描述如表1 所示。

表1 拓扑结构Tab.1 Topology structure

首先比较算法计算时延，实验环境为Intel Core i7-8700、3.20 GHz、32 GB RAM，Windows 7 操作系统。选择Dijkstra算法与PRA-TP、PRA-SLS 进行比较。随机选择路径并设置单链路故障，由于拓扑较小，为使测量时间更准确，分别对3种算法重复100 次实验，得到平均算法计算时延。实验结果如图6 所示，随着拓扑规模增大，3 种算法的平均计算时延均随之增加，其中Dijkstra 算法的平均计算时延最高。相较于Dijkstra 算法，PRA-TP 的平均计算时延降低了25%，PRA-SLS的平均计算时延降低了60%。虽然PRA-TP 需要两次最短路径计算，但每次被计算的拓扑均为分割后的拓扑，规模较小，因此整体时延较低；PRA-SLS 只需对一部分拓扑做一次计算，减小了时间开销，因此时延最低。

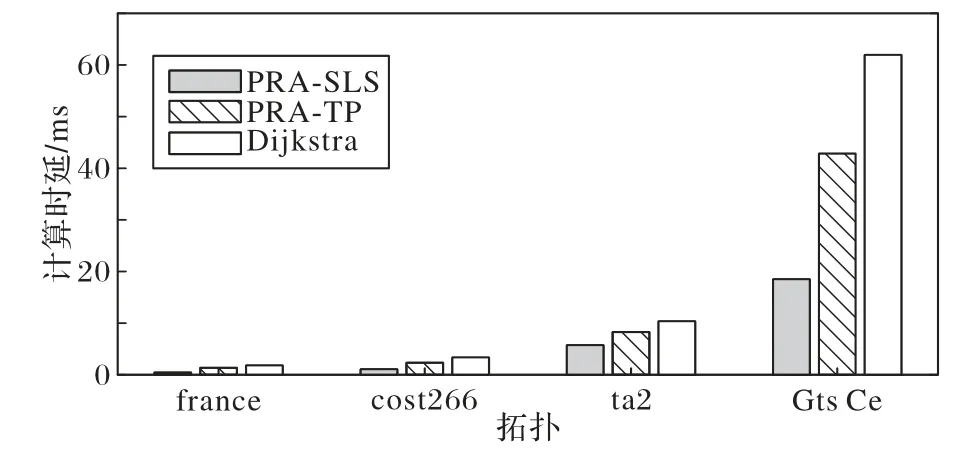
图6 算法计算时延对比Fig.6 Comparison of algorithm calculation delay

在PRA-TP、PRA-SLS 中，不同位置的故障链路切割出不同大小的Gs和Gt，会导致计算时延发生变化。在拓扑ta2 和拓扑Gts Ce 中，随机选择路径并设置单链路故障，使故障链路切割出不同大小的Gs，选择Dijkstra 算法与PRA-TP、PRA-SLS 进行比较，结果如图7、8 所示，横轴 |Es|表示Gs中边的数量，纵轴为计算时延。实验结果表明，不同的故障链路位置对Dijkstra 算法的时延没有影响。对于PRA-TP，在Gs中边的数量极小和接近原拓扑 |E|时，它的计算时延和Dijkstra算法计算时延基本相等；在Gs中边的数量接近原拓扑中边的数量一半时，PRA-TP 计算时延最低，相较于Dijkstra 算法相比，计算时延减小了接近一半。对于PRA-SLS，计算时延随着Gs中边的数量增多而不断降低，在Gs中边的数量接近原拓扑时，PRA-SLS 的计算时延最低，因为PRA-SLS 只需要对Gt进行遍历，Gt规模越小，时间开销越小。

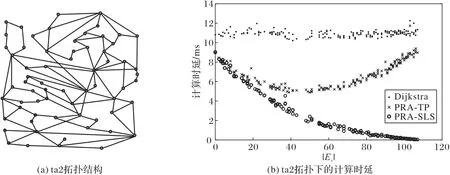
图7 ta2拓扑结构和计算时延Fig.7 ta2 topology structure and calculation delay

为比较路径恢复时延时，在Mininet 仿真平台上搭建拓扑ta2，随机选择路径并设置单链路故障，使故障链路在距离源节点不同位置处，由Ryu 控制器完成链路故障检测、路径选择及流表下发。选择Dijkstra 算法与PRA-TP 进行对比，实验结果如图9 所示。实验结果表明采用了PRA-TP 的恢复时延更短，相较于Dijkstra 算法，PRA-TP 的平均路径恢复时延降低了40%。这是由于路径恢复时延主要由故障发现时延、openflow 消息通道时延、算法计算时延和流表更新时延构成。由于实验中故障发现时延、openflow 消息通道时延相同，同一路径上的同一处链路故障，故障恢复时所需的流表更新时间也一致，因此计算时延更小的算法，恢复时延更短。此外，在拓扑ta2 中，不同位置的链路故障，在路径恢复时，流表更新次数不同，具有不同的流表更新时延，不同的流表更新时延也会影响路径恢复时延。

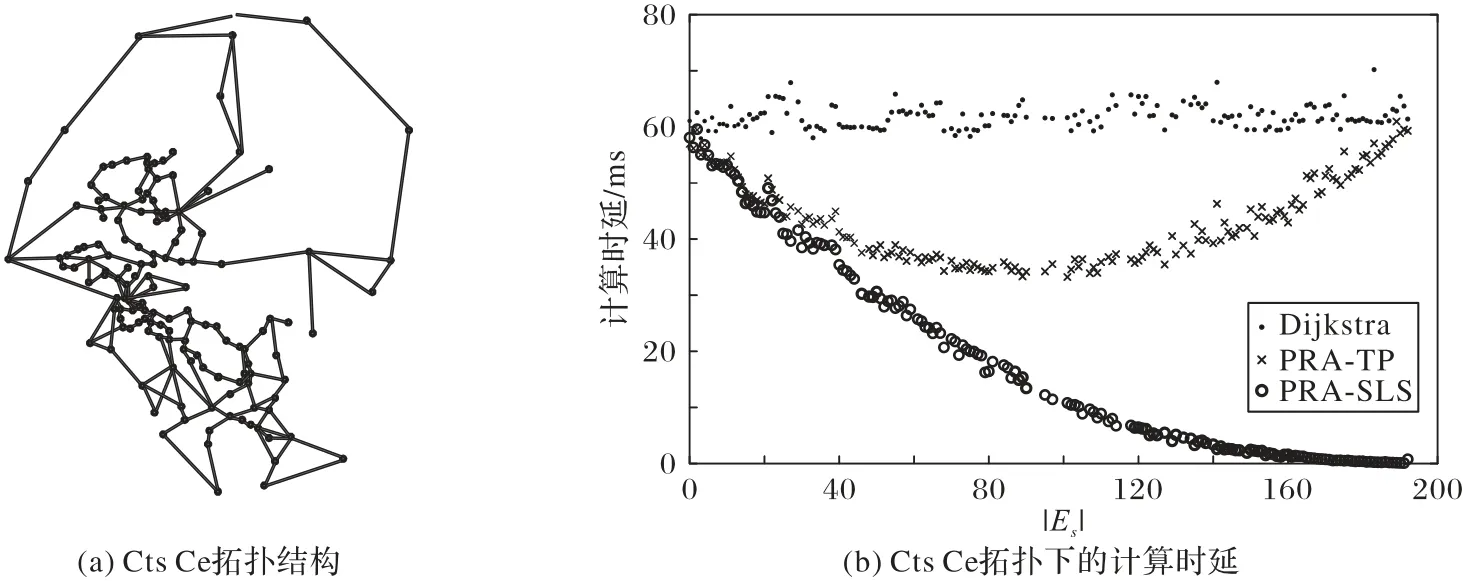
图8 Cts Ce拓扑结构和计算时延Fig.8 Cts Ce topology structure and calculation delay

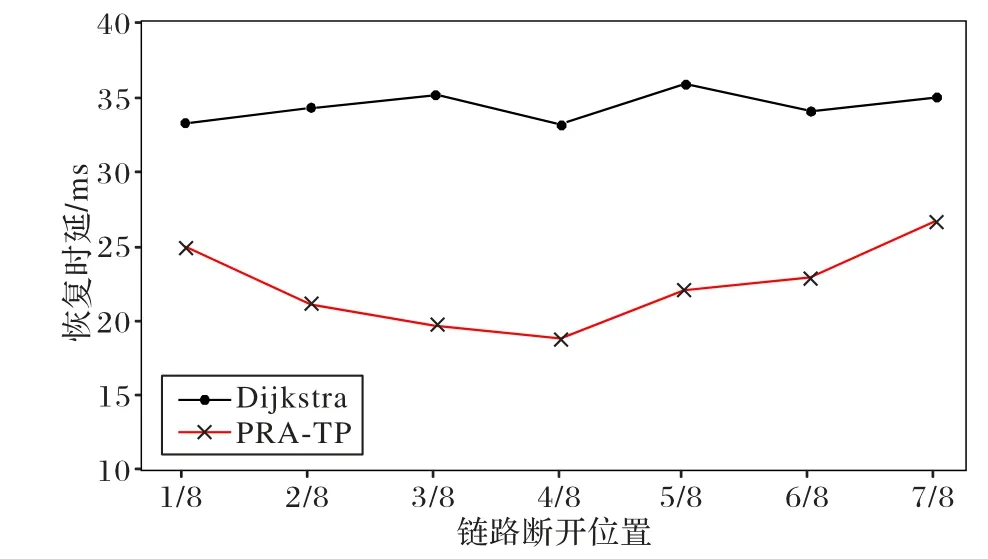
图9 路径恢复时延对比Fig.9 Comparison of path recovery delay

4 结语

本文针对SDIV 架构中车-路实时查询类通信场景中的单链路故障问题，同时考虑恢复过程时延和路径传输时延作为链路参数，对单链路故障恢复问题中的恢复时延进行建模，而后提出了基于拓扑划分的路径恢复算法（PRA-TP）和基于单链路搜索的路径恢复算法（PRA-SLS）。实验结果表明，本文综合考虑恢复过程时延和路径传输时延的方法以及两种算法能有效降低算法计算时延和路径恢复时延。对于PRA-SLS，故障链路位置越接近目的节点，算法计算时延越低，相较于Dijkstra 算法，PRA-SLS 的平均计算时延降低了60%；对于PRA-TP，故障位置划分的两个子树节点数目相近时，算法计算时延和路径恢复时延最低，相较于Dijkstra 算法，平均计算时延降低了25%，平均路径恢复时延降低了40%。但本文仅考虑了单链路故障的问题，无法应对多链路故障的情景，在下一步工作中，将研究多链路故障情况下的解决方案。