平面几何解题思路探析*
合肥师范学院数学与统计学院 唐亚军 唐永生 贺小雪 李亚文
1 问题提出
初中平面几何内容具有很强的实用性和基础性,它不但在现代生活和生产中的应用非常广泛,而且是进一步学习数学和其他学科必不可少的基础[1].其中,平面几何解题在培养学生的逻辑思维能力和科学的思维方法上起着非常重要的作用.但是学生在解答平面几何问题时,常停留在记忆与模仿的阶段,导致解题思维混乱,不知道从哪里入手以及需要遵循哪些规则等[2].因此,探析平面几何解题的最优化思路仍是数学教学研究的重要问题.
2 平面几何解题思路
波利亚指出,问题解决的模式是一个不断发展的过程,数学解题要探求解题模式的一般性.就平面几何而言,几何解题要严格遵守解题的各项规则,注重问题的识别与理解,注重制定与执行解决问题的条件和对结果的检验[3].教会学生解题的思路,有利于形成学生的解题心理定式,这样学生在不同的情境中都能快速地反应并解决问题.平面几何问题的解题思路如图1所示.

图1
2.1 问题情境
格式塔心理学派问题解决观认为,问题解决是对问题情境的整体理解.问题情境是个体所面临的数学问题以及由问题所引起的旧的知识结构的再现.学生在面临问题情境时,回想是否遇到过相似情境及其解决方法,或是以前的方法是否可以迁移.对问题的理解不同,学生思考问题的方向与思维习惯就会不同,进而所采用的方法也会不同.
2.2 数学阅读
阅读的目的是理解阅读材料,提取其中有意义的信息.平面几何解题中,数学阅读则是摒弃几何问题中的无关要素,对题设和图形进行分析,提取出解决问题的关键性信息.数学阅读是问题解决的起始环节和基础步骤.题设阅读是清楚所给的已知条件与结果,对题设所给的文字、符号等在脑海中进行预设与理解;几何图形阅读就是学生根据所学知识对所给图形进行识别.学生要善于将复杂的几何图形分解为有必然联系的简单基础几何图形去把握图形的本质[4],进而为后面的解题提供基础.(如图2所示)

图2
2.3 转化、分析、激活
转化,是指将题目中所给的数学语言(文字语言、符号语言、图形语言)进行转化,从而达到对问题的正确表征,把握问题的本质.分析,是指对已知条件与结果以及它们之间的关系进行分析.对已知条件的分析,即采用综合法,逼近结果,由条件可以顺推若干个几何关系T1,T2,……,Tn;结果分析,即采用分析法,逼近条件,由结果溯流而上可以逆推若干个几何关系Q1,Q2,……,Qn.推出条件T和Q的过程就是激活认知结构中条件与结果相关知识的过程.激活是一个搜寻与提取信息的过程,这个过程需要学生拥有非常丰富的知识结构.
2.4 构造联系
构造联系,是在分析条件与结果、激活相关知识的基础上,建立已知与未知之间的联系.比较T1,T2,……,Tn和Q1,Q2,……,Qn,如果其中的Ti和Qi之间存在明显的关系或者Ti=Qi的话,通过综合与分析,便可以构造未知与已知之间的联系[5],这样问题便得到了解决;若比较T1,T2,……,Tn和Q1,Q2,……,Qn,通过已有的条件很难将两者联系起来,条件与结论之间存在着中间的未知条件M1,M2,……,Mn,其中有条件Mi存在于Ti和Qi之间,沟通了Ti和Qi或者Ti=Mi=Qi,从而顺利地从条件到结果.未知条件M往往是通过巧妙地添加辅助线而得到,因此,一条好的辅助线往往能使复杂的问题变得简单,辅助线的建立是解题的关键一步.(如图3所示)

图3
2.5 回顾整理
回顾,即重新思考分析问题的认知过程,是一种对自我认知的检查.分析问题的时候难免会出现思维与逻辑上的错误,即使是正确的分析过程和解题思路,也要在回顾的过程中进行调整、修改、补充等,寻求解答过程的最优化.整理,即整理分析过程,在这过程中,要注意数学语言的正确使用,尽量多使用数学符号语言,力求过程的精简化;过程要符合语义和法则,注意正确把握各步骤间的逻辑推导关系.
3 平面几何解题思路的应用
安徽省合肥市2021年压轴题第21题是一道几何题,非常典型,尤其是第(3)小问非常考验学生的解题思维.
例如图4-1,在四边形ABCD中,∠ABC=∠BCD,点E在边BC上,且AE∥CD,DE∥AB,作CF∥AD交线段AE于点F,连接BF.
(1)求证: △ABF≌△EAD;
(2)如图4-2中,若AB=9,CD=5,∠BCF=∠AED,求BE的长;


图4-1
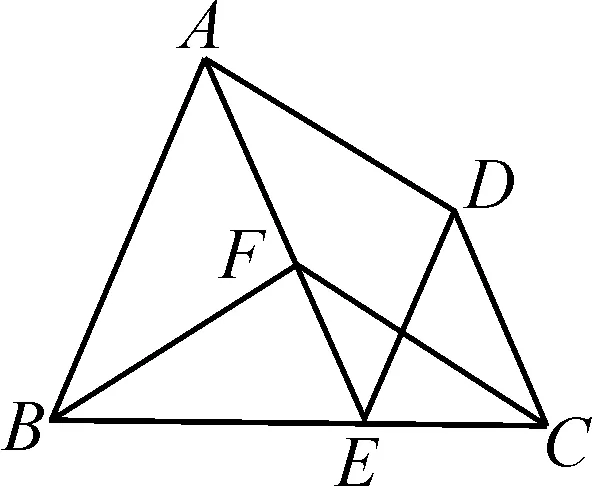
图4-2

图4-3
问题情境:这种多个问答的问题往往前一问的方法或者结论可以为下一问做参考.
数学阅读:题干中给了7个条件,即四边形ABCD,∠ABC=∠BCD,点E在边BC上,AE∥CD,DE∥AB,CF∥AD,CF与AE交于点F;所给图形中,以三角形为主,这个复杂的图形可以看成:△ABE和△DEC顶点相连,也可以看成△ABE与梯形AECD拼成.问题(1)是证明全等;(2)是给定值,然后求BE的长;(3)中给定BF的延长线过AD的中点M,求比值.
转化:将上述需要转化的条件进行如下语言的转化,

分析与激活:对已知条件进行如下分析.
①AE∥CD⟹∠AEB=∠DCE,∠AED=∠CDE,∠DCF=∠CFE;②DE//AB⟹∠ABE=∠DEC,∠BAE=∠AED;③∠ABC=∠BCD⟹∠ABE=∠AEB= ∠DEC=∠DCE⟹△ABE与△DEC为等腰三角形⟹AB=AE,DE=DC;④由①和②条件⟹∠BAE=∠AED=∠CDE;⑤CF//AD⟹∠DAF=∠CFE⟹∠DAF=∠CFE=∠DCF;⑥由③⑤⟹AFCD是平行四边形⟹AF=CD⟹AF=CD=DE.
对第(1)问进行分析:(1)要求证△ABF≌△EAD⟸只需满足SSS,SAS,ASA,AAS中的一个⟸边角等量关系.
解析:(1)由上面分析可知,在△ABF和△EAD中AB=AE,∠BAE=∠AED,AF=DE,所以 △ABF≌△EAD(SAS).
由△ABF≌△EAD,可得AD=BF=CF,∠DAF=∠ABF=∠CFE=∠DCF.

解析:(2)由上述分析可知△ABE∽△BFE,则
因为AE=9,EF=4,所以BE2=36,即BE=6.



4 平面几何解题思路的思考
任何解题的教学都是在学生已有的知识基础之上的再发现、再建构的过程,在这个过程中学生对自己的思维进行监控与调整.
4.1 学生的认知结构是解题思路的基础
学生的已有知识总量和知识贮备方式等主观因素是问题解决的根本因素.认知结构是学生由知识结构内化而形成的,是学生将学得的知识按照自己的理解组织起来的心理系统,它既是知识的建构方式,也是知识的贮备方式.学生头脑中知识的良好结构和联系与问题解决之间存在着明显的相关性[6],可以快速进行知识提取,全面激活关于条件与结论的相关知识点,更好地促进问题解决.任何解题思路都离不开学生原有的知识与经验,这是学生学习的基础.
4.2 解题思维过程的整体推进
解题步骤不是前后相继的关系,而是在某个环节的基础上同时进行的.学生在阅读的同时,也进行着转化的操作,边阅读,边理解,边转化,这样才能更加透彻地把握题目的全部内容.当转化到一定的条件时,也就开始了分析与激活.因此,这几个环节是环环相扣、不可分离的关系.后面步骤是在前面步骤的基础上展开的,但此时并不意味着前面步骤的结束.
4.3 根据问题难易程度做出相应调整
虽然研究几何解题思路是为了学生更好地解决问题,但是一味按照思路来解题势必限制学生的思维,形成思维定式.因此,在几何解题的过程中,应该根据问题的难易程度做出相应的调整、删减等.对于稍微简单一点的问题,在转化的过程中就可以将问题解决;对于比较难的数学证明,则需要在分析的基础上多次阅读与转化.
5 结论
平面几何解题的过程中,学生的心理与思维起到关键的作用.学生提取自己的认知结构,对自己解题过程进行监控,从而使问题得以解决.因此在教学中教师应该注重培养学生数学阅读能力,完善学生认知结构,提高学生自我元认知,以此培养学生的几何思维,提高学生的平面几何的解题能力.

