基于阻抗辨识的沽源地区风电并网系统次同步振荡控制策略

薛 峰，吴家龙，崔晓丹，冯佳期，许剑冰，徐海波

（1.南瑞集团有限公司（国网电力科学研究院有限公司），江苏省 南京市 211106；2.智能电网保护和运行控制国家重点实验室，江苏省 南京市 211106）

0 引言

中国河北沽源电网是一个典型的大规模风电集群经串补送出系统，风电装机占比达80%以上，区域内无同步机组。近年来，该地区电网发生了多起次同步振荡事件，严重威胁电网的安全稳定运行和新能源消纳［1］：2010 年10 月首次出现谐振，2012 年12 月 出 现4 次 振 荡，2013 年6 月 出 现1 次 振 荡，2016年4 月、6 月、7 月共计出现4 次振荡，振荡频率为4～8 Hz［2］。风机附加阻尼控制［3］、站内加装柔性交流输电系统（FACTS）设备［4］、电网网架“三站四线”切改［5］等措施一定程度上减少了次同步振荡的频次。随着该地区新能源装机规模增大，次同步振荡风险依旧存在，目前现场一般采取退出送出线路串补的方式抑制振荡［5-6］。这不但缺乏量化分析的依据，而且因削弱电网强度存在产生次生安全稳定问题的风险。总之，多年来该地区存在的次同步振荡问题一直未能有效解决。

为防止次同步振荡演化扩大影响电网安全运行，当前各相关地区部署了宽频振荡控制系统（或宽频振荡监测系统）［5，7-9］：基于安全稳定控制装置识别振荡，并通过切除相关风场馈线来实现振荡抑制。然而其控制策略缺少成熟的机理依据，适应性不足往往导致控制措施粗放。文献［10］介绍了目前工程上常用的基于振荡分量幅值整定的控制策略，认为振荡相对幅值越大，切除相应馈线对振荡抑制越有效，但大量仿真表明，采用该方法切除风场馈线后可能加剧振荡。文献［11］提出采用阻抗法来分析和抑制次同步振荡，将风电并网系统聚合成RLC 电路模型，基于阻抗分析得到次同步振荡机理及参数灵敏度，但并未提出有效的控制策略。文献［12-16］指出由于阻抗耦合特性，不能简单地将系统划分为正负序解耦系统进行判稳，提出通过耦合项等效形成单输入单输出系统。文献［15-16］指出可以通过求取高阶阻抗模型特征根或基于广义奈奎斯特判据判稳，但难以应用于实际系统，因为该方法需要阻抗的全频域模型，而实际系统阻抗拓扑难以获取，振荡路径存在不确定性。总之，当前的次同步振荡控制存在应用于实时控制的动作判据缺失、新能源馈线及电网阻抗时变性［17-18］导致阻抗辨识难［19］等问题。

为此，本文针对沽源地区大规模并网系统次同步振荡的实际场景，提出基于阻抗分析方法的稳控装置动作判据及基于阻抗辨识的次同步振荡控制策略。针对实际电网中系统阻抗难以准确获取的痛点，提出了电网侧阻抗极限值预估方法和风场支路阻抗在线测量方法。最后，利用沽源地区实际电网数据，构建了基于PSCAD/EMTDC 的电磁暂态仿真平台，验证了所提次同步振荡控制策略的有效性。

1 次同步振荡控制原理及策略

1.1 基于阻抗法的次同步振荡控制原理

本文所提次同步振荡控制的主要思路是采用稳控装置识别主导次同步振荡频率下的系统等效正负序阻抗，通过阻抗判据切除部分风场馈线，使切除后系统阻抗满足稳定条件。下面以多风场经串补长线路并网引发的次同步振荡机理分析系统为例，介绍适用于大规模风电并网系统次同步振荡控制原理及判据，典型结构如附录A 图A1 所示。对于关注的振荡频率，可以采用系统聚合阻抗的振荡特性量化分析方法［11］。在谐振点ωs附近，系统聚合阻抗虚部为0；在次同步振荡频率fs邻域{f|0 ≤|f-fs|＜h}（h为一个很小的正常数）内，系统聚合阻抗可以表征为：

式中：Zsys(f)、ZL(f)和ZW(f)分别为系统总阻抗、电网侧阻抗和风场总阻抗；RΣ(f)和XΣ(f)分别为聚合电阻和聚合电抗。

次同步振荡在频率fs时的稳定性可以通过聚合电阻和聚合电抗斜率乘积的正负来确定，对于风电并网系统来说，次同步振荡点处的电抗斜率通常为正，因此其稳定性由聚合电阻正负值决定［8］。如果通过稳控装置切除部分风场馈线来改变系统阻抗，使其满足式（2），那么在次同步振荡频率fs下系统稳定。

式中：下标p 和n 分别代表正序和负序。

根据式（1）和式（2）可知：

1）通过切除若干风场馈线，使得次同步振荡频率fs下系统阻抗实部大于零，可消除次同步振荡，此为基于阻抗法的次同步振荡控制的动作判据。

2）计算系统阻抗时，需要获取电网侧和各风场支路的阻抗，阻抗辨识的精准度直接决定了稳定性判断的准确性。

1.2 基于阻抗法的次同步振荡控制策略

假设大规模风电并网电力系统含N个风场支路（见附录A 图A1），系统发生次同步振荡时，稳控装置实时采集主要线路在次同步振荡频率fs下的有功振荡分量。当振荡分量达到预设阈值时，实时测量各风场馈线在次同步振荡频率fs下的阻抗并计算系统总阻抗。按切除1 个到N个风场馈线的次序，分别计算各切除方案下系统总阻抗，如果切除风场组合中i(i≥1)个馈线时的系统总阻抗满足式（2），则说明存在有效抑制次同步振荡的切除方式，将停止进一步试探切除更多馈线的其他方案。

按照排列组合，切除i(i≥1)个风场馈线的切除组合方式有种，对应需要计算个系统总阻抗值，将其中第k种切除组合对应的系统正序阻抗记为：

式中：Zsys，ik，p和ZW，jk，p分别表 示 切除i个风场 的第k种切除组合下系统总正序阻抗和风场总正序阻抗。电网侧正序阻抗ZL，p可通过离线方式计算得到，系统负序阻抗计算关系同式（3）。如果种切除方式中存在多种组合满足式（2），即均可以抑制次同步振荡，则选择切机量最小的方案作为最终切机策略。

理论上，只要正负序阻抗同时满足式（2），则该频率下系统稳定，但考虑到实际工程中稳控装置测量存在误差，且切除部分风场可能造成振荡频率偏移，如果按当前次同步振荡频率下序阻抗值切除风场后次同步振荡无法消除，还可通过迭代继续追加“切机”轮次，确保次同步振荡得到抑制。基于阻抗法的次同步振荡控制策略流程如图1 所示。

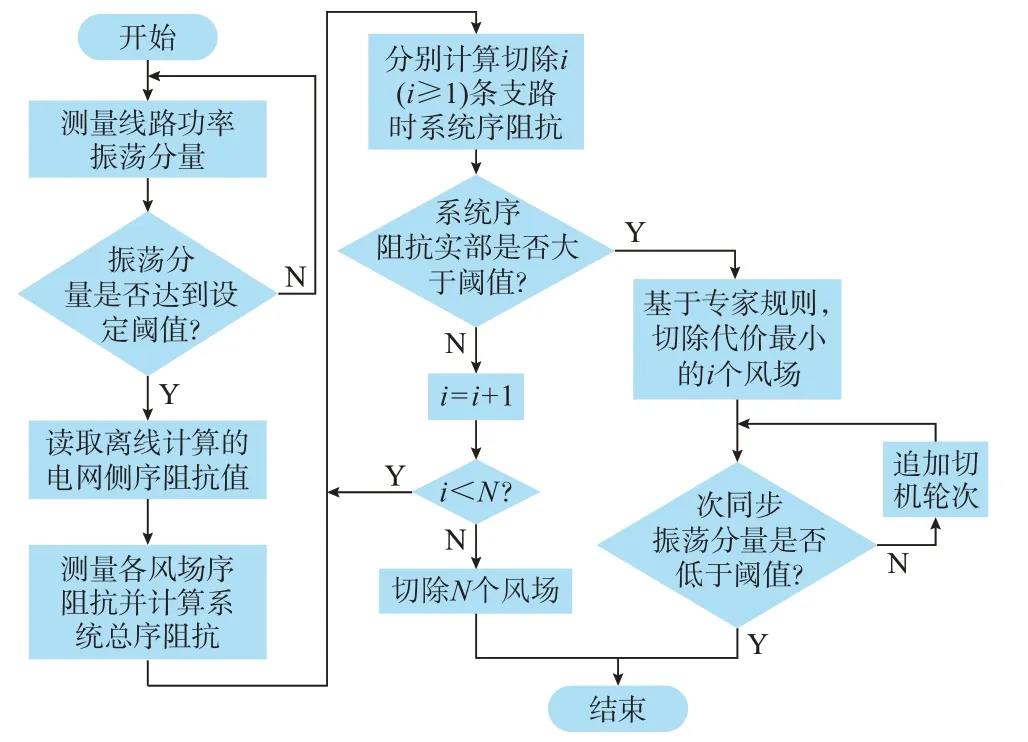
图1 基于阻抗法的次同步振荡控制策略流程图Fig.1 Flow chart of control strategy of sub-synchronous oscillation based on impedance method

2 系统阻抗辨识方法

2.1 电网侧阻抗辨识

对于实际系统来说，电网侧一般由包含源网荷的复杂线路串并联而成，在线辨识电网侧阻抗难度极高。理论上，可以通过测量各节点次同步电压和各支路次同步电流识别出次同步振荡路径，然后依据识别出的网络拓扑，根据预先获得的线路参数聚合得到电网侧阻抗。但是，考虑到实际电网中次同步振荡路径及范围的不可预知性，不可能针对每个节点布置测量装置，加之电网侧阻抗受运行方式影响较大，在实际电网计算过程中，不可能获取准确的电网侧阻抗值。

从式（1）和式（2）可知，在其他条件不变的情况下，电网侧聚合电阻越小，系统越容易发生次同步振荡。即如果电网侧聚合电阻最小的运行工况下的振荡得以抑制，那么其他任何工况下的振荡都能够被抑制。因此，通过离线求取电网侧聚合电阻最小值，将该值用于次同步振荡控制策略的计算过程中，就可以得到满足任意电网运行方式下的“切机”策略。需要说明的是，通过离线求取电网侧聚合电阻最小值得到的控制策略具有一定保守性，可能会存在风场“过切”的情况，但是只要满足一定裕度，工程上是允许的。因此，本文提出一种电网侧聚合电阻极限值预估方法。

风电集群一般通过长线路并入大电网，假设发生次同步振荡的系统中各风场经过多条长距离线路分别接入区域电网1、区域电网2、…、区域电网j、…、区域电网m，如附录A 图A2 所示，可求得电网侧阻抗Z为：

式中：Zgj=Rgj+jXgj为区域电网j的阻抗；ZLj=RLj+jXLj为 线 路 阻 抗；下 标j∈[1，m]表 示 电 网 编号，其中，m为区域电网总数。

电网侧聚合电阻为：

根据式（5）可知，电网侧聚合电阻最小值就是求多元变量函数RLine，total的最小值，下面分3 种情况介绍求取方法。

1）如果函数RLine，total在定义域内二阶连续可导，且存在驻点，那么可以联立如下方程。

通过式（6）可以求得所有驻点，令驻点是长度为2m的一维向量M，引入黑塞（Hessian）矩阵H(M)，求出所有极小值。一般来说，电网j阻抗的实部和虚部均会被限定在某一区域范围内，即Rgj∈[Rgj，min，Rgj，max] 和Xgj∈[Xgj，min，Xgj，max]，其 中，j∈[1，m]。如果函数RLine，total在闭域区间连续，那么函数RLine，total在闭域区间上可求得最小值，其最小值可能为区域内极小值，也可能为边界最值，取所有的极小值及边界最值中的最小值，即为函数RLine，total在闭域区间内的最小值，这样就得到了电网侧聚合电阻的最小值。

2）如果函数RLine，total在定义域内一阶可导且无驻点，但是存在严格单调性，即存在式（7）或式（8），那 么，函 数RLine，total在 闭 域 区 间Rgj∈[Rgj，min，Rgj，max]和Xgj∈[Xgj，min，Xgj，max]内的最小值为边界最值。

3）如 果 多 元 变 量 函 数RLine，total无 法 通 过 构 建Hessian 矩阵或者基于单调性求取电网侧聚合电阻最小值，则可以采用优化算法获取。将函数RLine，total作为 目 标 函 数 ，Rgj∈[Rgj，min，Rgj，max] 和Xgj∈[Xgj，min，Xgj，max]作为约束条件，利用计算机迭代寻优［20］得到的目标函数最小值就是电网侧聚合电阻最小值。

2.2 基于稳控装置的风场支路阻抗在线测量

当存在频率耦合特征的风电机组通过线路并网时，以端口处注入正序扰动电压为例，风电机组并网系统各频率分量耦合关系［21］见附录B 图B1。根据文献［12-14，21］可知，风电机组的公共连接点（point of common coupling，PCC）考虑频率耦合等价 折 算 后 的 正 序 导 纳Yinv，p和 正 序 阻 抗Zinv，p分 别 为：

由于风电机组并网线缆一般为三相平衡的无源线路，不存在频率耦合特征，线路在频率fs和fc时阻抗可以分别表示为ZLs和ZLc。风电机组经长线路并网，馈线端口处等价正序阻抗表示为：

同理可以求出等价负序阻抗。

实际工程中，稳控装置安装在风场馈线上，需实时测量主导次同步振荡频率下风场各馈线阻抗，从而用于计算候选控制策略下的系统总阻抗。然而，实际风场参数很复杂且难以辨识，阻抗在线测量尚无成熟的实施方法。本文参考风电机组的等价序阻抗的计算方式，从式（10）可知，频率fs下的序阻抗为该频率下序电压扰动分量与同频率同相序电流响应分量的比值。基于次同步振荡稳控系统实际场景及工程需求，采用基于波动量法［22］的风场馈线支路阻抗在线测量的工程方法（见附录B 图B2），通过提取风场馈线端口次同步振荡时电压和电流序分量，风场馈线处的正序阻抗为：

3 基于实际电网的分析验证

基于沽源地区电网某一典型运行方式数据，对风场做如下简化处理：如果沽源（或察北）下属馈线支路含多个风场，那么该支路只保留一个等效风场，该等效风场的风机单元类型数量、控制参数和集电系统根据实际电网数据进行适当化简［23］。简化后的沽源地区风电并网系统网架结构如图2 所示。实际工程中配置了2 个稳控主站，分别为沽源站和察北站。沽源站下属的4 个风场和察北站下属的6 个风场馈线处均部署稳控子站。整个系统阻抗分为电网侧阻抗和风场总阻抗，电网侧阻抗采用离线计算方式获取，风场支路阻抗采用稳控装置在线测量，并基于拓扑结构计算风场总阻抗。沽源风电并网系统网架及测量布点如图2 所示。

3.1 沽源地区电网侧阻抗极限值预估

如图2 所示，沽源风电并网系统电网侧拓扑侧阻抗包括变压器阻抗ZT、汗沽线阻抗ZL1、太沽线阻抗ZL2、内蒙古电网等效阻抗Zg1和华北电网等效阻 抗Zg2，其 中，Zx=Rx+jXx(x=L1，L2，g1，g2)。ZT、ZL1和ZL2可以通过拓扑参数聚合获得，内蒙古电网和华北电网中拓扑连接关系复杂，次同步振荡路径无法准确获取，Zg1和Zg2两个阻抗需做极限预估。将沽源500 kV 母线到内蒙古电网以及沽源500 kV 母线到华北电网等效成附录B 图B3 所示的电路拓扑，线路并联后的等效阻抗为：

通过式（10）计算得到的等效阻抗的实部为：

式中：A=RL1+Rg1，B=RL2+Rg2，C=XL1-Xg1，D=XL2-Xg2。

内蒙古电网及华北电网阻抗实部和虚部取值范围的计算方法为：遍历计算所有典型运行方式下的电网阻抗，选取其实部及虚部的最大值和最小值作为其取值范围。即多变量函数RLine，total为闭域区间函数，其 变 量 取 值 范 围 为：RL1∈[RL1，min，RL1，max]，RL2∈[RL2，min，RL2，max]，XL1∈[XL1，min，XL1，max]，XL2∈[XL2，min，XL2，max]。一 般 而 言，电 网 呈 阻 感 特 性，RL1，min、RL2，min、XL1，min和XL2，min均大于0。根据2.1 节，通过MATLAB 可知函数RLine，total在区间范围内无驻点，其一阶偏导函数为：

根据2.1 节可知，函数RLine，total在(RL1，min，RL2，min，XL1，min，XL2，min)处可取得最小值，即此处电网侧阻抗实 部 最 小。 采 用RLine，total(RL1，min，RL2，min，XL1，min，XL2，min)得到的次同步振荡控制策略适用于任意运行方式下内蒙古电网和华北电网，同步求出电网侧阻抗值为ZLine，total。

3.2 沽源地区风场总阻抗辨识

沽源地区风场总阻抗包括沽源220 kV 母线下属所有风场支路、沽察线和察北站下属所有风场支路的阻抗。所有风场支路阻抗测量位置如图2 所示，采用2.2 节中的在线阻抗测量方法，对于并联的风场，直接测量支路导纳将更便于进行下一步运算。

定义察北站下属第i个风场的导纳值为YWCBi，那么察北站的总阻抗ZWCB，total为：

式中：YWCB，total为察北站的总导纳。

沽察线的线路阻抗可通过拓扑参数直接计算得到，记 为ZGC，line。沽 察 线 和 察 北 站 的 总 导 纳YGC，total为：

假设沽源220 kV 母线下属第k个风场的导纳值为YWGYk，那么沽源220 kV 母线下属所有风场的总导纳YWGY，total为：

沽源地区的风场总阻抗ZWind，total为：

沽源地区系统总阻抗Zsys为：

由式（2）可知，当沽源风电并网系统发生次同步振荡时，需要保证切除风场后的系统阻抗实部Re(Zsys)＞0，系统次同步振荡消除。

3.3 基于实际电网的控制策略仿真验证

基于PSCAD/EMTDC 构建沽源地区大规模风电并网系统电磁暂态仿真研究平台，对阻抗辨识方法及控制策略进行验证。通过降低风速激发次同步振荡，对沽源220 kV 上送线路电流进行监测，对其进行快速傅里叶变换（FFT）分析，得到电流谐波分量分布图，如附录C 图C1 所示。可以看出，次同步振荡电流的主导频率为8 Hz。

按照1.2 节的次同步振荡控制策略，当检测到次同步振荡分量超过设定阈值，开始测量各风场支路阻抗，并按式（19）计算系统阻抗。如附录C 图C2所示，系统出现次同步振荡时，其系统正、负序阻抗实部计算结果分别为-0.086 Ω、-0.081 Ω（称之为“不切除风场馈线时系统阻抗实部”）。此时，正、负序阻抗实部均为负值，阻抗辨识结果与系统振荡情况相符。根据式（2）给出的次同步振荡阻抗判据，如果切除风场后，系统总序阻抗实部为正，那么次同步振荡即可抑制。

3.3.1 切除1 条风场馈线后系统阻抗计算及仿真验证

根据第1.2 节的次同步振荡控制策略，首先计算仅切除1 条风场馈线后的系统总阻抗。如图2 所示，简化后的沽源风电并网系统包含10 个风场，切除1 条风场馈线的方式有种，分别计算不同切除方式对应的系统总阻抗实部，结果如附录C 图C2 所示。可以看出，正、负序阻抗实部都小于0，这意味着，该工况下，切除任意1 条风场馈线均无法抑制次同步振荡。从基于阻抗法的计算结果来看（切除后系统阻抗计算值更加接近0），切除恒泰、莲花、九龙风场馈线能改善振荡，切除其他风场馈线会加剧振荡。在PSCAD/EMTDC 中对切除1 条风场馈线进行仿真验证，图3 所示为分别切除恒泰和友谊风场馈线后的两次仿真结果。可以看出，在12 s 后，切除恒泰风场馈线后次同步振荡电流分量变小，振荡得以改善；切除友谊风场后次同步振荡电流分量变大，会加剧次同步振荡。仿真结果与基于阻抗法的计算分析结果一致。

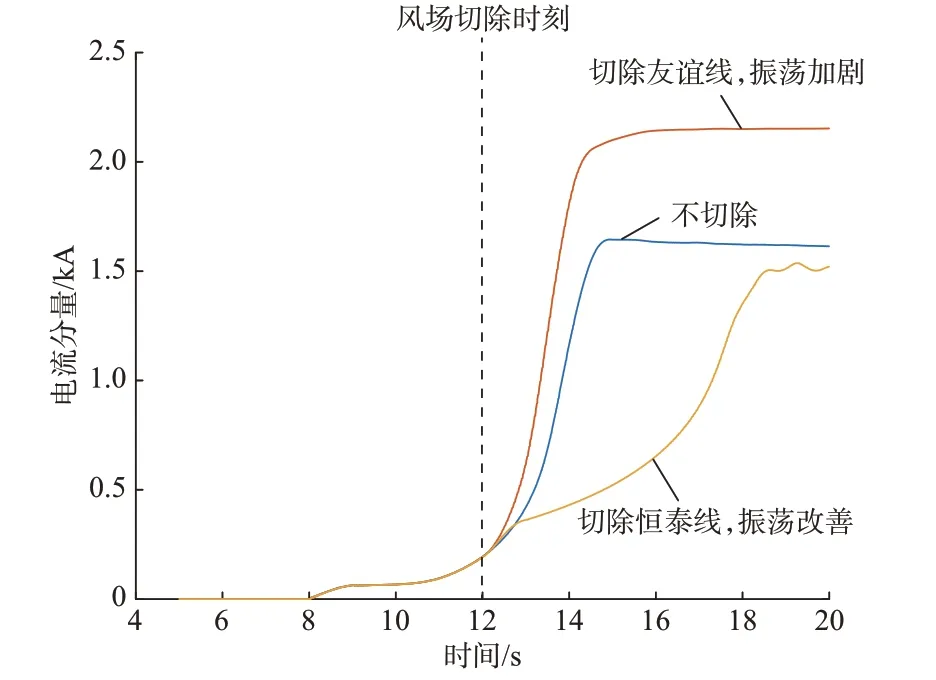
图3 切除1 条风场馈线后次同步振荡电流分量仿真结果Fig.3 Simulation results of sub-synchronous oscillating current component after removing one wind farm feeder

3.3.2 切除2 条风场馈线后阻抗计算及仿真验证

根据前文仿真结果可知，切除1 条风场馈线无法抑制系统次同步振荡。根据控制策略，需要计算切除任意2 条风场馈线后的系统总阻抗。切除2 条风场馈线的方式有种，选取几种典型切除方式计算对应的系统总序阻抗实部，如附录C 图C2 所示。由此可知，分别切除恒泰和莲花、九龙和恒泰、天立和恒泰、九龙和莲花中任一组合的风场馈线后，均可以完全抑制次同步振荡；切除天立和莲花、九龙和天立中任一组合可以改善振荡；同时切除察北下属任意2 条风场馈线，均会加剧次同步振荡。在PSCAD/EMTDC 中进行仿真验证的结果如图4 所示。可以看出，同时切除恒泰和莲花后次同步振荡电流分量逐渐消失，次同步振荡得到抑制；同时切除天立和莲花，次同步振荡电流分量减小。切除东湾和绿脑、友谊和绿脑任一组合后，次同步振荡电流分量变大，会加剧次同步振荡。仿真结果与基于阻抗法的计算分析结果一致。

图4 一次性切除2 条风场馈线后次同步振荡电流分量仿真结果Fig.4 Simulation results of sub-synchronous oscillating current components after removing two wind farm feeders at one time

综上所述，基于阻抗法的计算结果与基于PSCAD/EMTDC 的仿真结果相互验证，表明所提控制策略可行。

4 结语

本文提出了一种基于阻抗辨识的次同步振荡控制实现框架及计算方法，解决了实际电网中电网侧阻抗和风场阻抗难以准确辨识的问题，为采用稳控装置对电网中实际发生的次同步振荡进行控制提供了关键思路和方法。主要结论如下：

1）仿真结果表明，不合理的风场切机策略不但无法消除次同步振荡，还可能加剧振荡。基于阻抗法的次同步振荡控制机理明确，恰当的风场切机策略可保障系统电阻为正，系统次同步振荡能得到有效抑制。

2）通过电网侧阻抗极限值离线预估和风场支路阻抗实时测量方法得到稳控系统切除风场馈线组合方案下的系统总阻抗，进而确定次同步振荡控制策略；按照切除更少的馈线或切除相量馈线数量下切除容量更少的原则选择切除组合，保障了控制的经济性；实时监视、量测、计算以及迭代追加轮次的总体框架思路保障了所提控制策略的工程可靠性和有效性。

文中着重研究了应对次同步振荡的控制实现方法，但其技术思路和策略计算方法同样适用于高比例新能源并网系统下中低频振荡控制。下一步，将深入研究所提方法在其他复杂振荡场景下的适应性，并通过现场实际应用迭代完善。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。