实验室内细颗粒泥沙沉降速度与悬沙浓度关系评估

唐杰平，陈德志，李高聪

（1.广东海洋大学电子与信息工程学院，广东 湛江 524088；2.自然资源部第四海洋研究所，广西 北海 536009）

悬浮泥沙的沉降速度是沉积动力学中一个重要参数，准确获得泥沙沉降速度数值，对于使用数值模型评估沉积物分布、扩散和输运等至关重要。影响泥沙沉降速度的因素很多，例如泥沙粒径[1-2]、悬沙浓度[3]、水体物理特征[1]和絮凝[4]等。尤其对于细颗粒黏性泥沙，在悬沙浓度较低时，絮凝作用明显，而当悬沙浓度较高时，会形成沉降阻碍效应，这使得准确评估泥沙沉降速度变得十分困难。很多学者一直致力于使用简单的理论数学公式来表达泥沙沉降速度。目前，获取泥沙沉降速度的方法主要有两种：①使用半经验半理论公式；②通过现场或者室内实验测量。经验公式法最早可以追溯到150 多年前，Stokes 通过实验给出了计算球形泥沙颗粒的沉降速度经验公式[1]。Dietrich 于1982年在Stokes理论公式的基础上，针对自然界中形状不规则泥沙颗粒，提出了改进的泥沙沉降速度计算公式[2]。到目前为止，对于黏性细颗粒泥沙的沉降速度，考虑阻碍沉降效应，学者们也总结了很多半经验半理论的数学公式[4-8]。然而，这些经验公式中的参数对于不同区域的泥沙，由于泥沙颗粒差别很大且所处环境不同，直接使用这些经验公式评估泥沙沉降速度会导致较大的误差。

通过现场实验获得悬浮泥沙沉降速度主要依据平衡扩散理论。当泥沙分布处于动态平衡时，在垂向上：水流驱动导致的向上扩散的泥沙质量等于由于自身重力作用导致的向下沉降的泥沙质量。LI Y等[7]在2018年使用先进的海洋仪器，测量了高频的悬沙浓度和流速数据，然后使用平衡方程结合“box”模型，评估了泥沙沉降速度，该方法的结果最为准确，但是受测量精度和野外动力条件复杂等因素影响，原始数据获取难度大、成本高，计算结果的稳定性无法得到有效保障。典型的室内测量泥沙沉降速度的实验方法有Griffth 沉降管法、底部取样管法（Bottom Withdraw Tube，BWT）、改进底部取样管法（Modified Bottom Withdraw Tube，MBWT）和重复深度吸管法[9-11]，然后使用Oden 理论[12]或者Exact 理论[11]对实验数据进行分析，进而评估泥沙沉降速度。上述室内实验方法均需要在沉降过程中采集水样，取样过程容易对泥沙沉降产生影响，并且实验装置均为专门定制，增加了实验难度。

本文在重复深度吸管法基础上进行改进，介绍了一种更加简捷有效的室内实验方法——静水沉降实验。实验泥沙样品采集于野外现场，本实验结果可以表征当地沉积物沉降速度特征，其结果可以用于数值模型计算。

1 材料与方法

1.1 室内静水沉降实验

本文静水沉降实验中使用的悬浮泥沙样品，来自2017年3 月至4 月在废黄河口采集的100 L 海水样品。水样带回实验室之后，首先静置48 h，使悬浮泥沙全部沉降到容器底部，然后将上层清澈海水和底部泥沙分离开来，清澈海水保留20 L 满足实验使用即可，其余海水废弃。选择容量约30 L的水桶作为标定桶，将海水和泥沙全部放入标定桶中，同时在距离水面0.05 m、0.15 m、0.25 m 3 个层位各放置一个浊度计（图1）。本实验中使用的浊度计为光学后向散射浊度计（OBS-3A，Campbell Scientific 公司），该仪器可以测量水体浊度和电导率。然后，使用搅拌器搅拌海水水样，使得桶中泥沙颗粒均匀悬浮分布，之后，停止搅拌，让泥沙在重力作用下自然沉降，同时使浊度计开始工作，测量3 个层位海水的浊度值。一直持续至海水变得清澈，浊度计浊度值停止下降时，结束实验。从以上实验中，我们将获得静水条件下，距离水面0.05 m、0.15 m 和0.25 m 3 个层位的海水浊度时间序列数据。要计算泥沙颗粒沉降速度，还需要将浊度计测量的浊度数据转换成悬沙浓度数据，因此，还需要对浊度计进行标定。

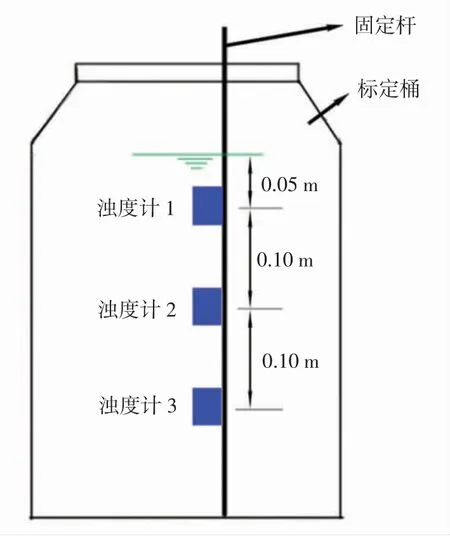
图1 室内静水沉降实验装置

1.2 悬沙浓度标定

悬沙浓度是影响悬浮泥沙沉降的一个重要因素，在上述静水沉降实验中浊度计测量获得的是水体浊度值，因此，需要将浊度值转换为悬沙浓度。要将浊度值转换为悬沙浓度值，需要对浊度计进行标定，确定每个浊度计的浊度值和悬沙浓度之间的线性关系，具体步骤如下：①通过静置沉降，将海水和悬浮泥沙分离，清澈海水放置于标定桶中，泥沙样品放置于烧杯中；②将浊度计固定在清澈海水中并使仪器开始工作；③向清澈海水中添加少量泥沙样品，使用搅拌器将泥沙搅拌均匀，使水体浊度上升约100 NTU，等待浊度计的浊度值稳定之后，记录此时各个浊度计测量的浊度值和电导率；④在执行③步骤中记录浊度数值的同时，采集水样，记录水样体积，并使用0.45 μm 滤膜（滤膜提前烘干称重） 对水样进行过滤，然后，对过滤后的滤膜进行烘干、称重，从而计算得到水样的悬沙浓度；⑤重复③④两个步骤，直至泥沙样品消耗完毕。最终，可以获得每个浊度计不同浊度值对应的悬沙浓度数值，以此建立各个浊度计的浊度值与悬沙浓度之间的线性关系。

光学浊度计虽然拥有很好的测量精度，但是量程一般有限，研究表明当悬沙浓度小于10 g/L 时，浊度值与悬沙浓度之间有着较好的线性关系[13]。但是，当悬沙浓度过大时，浊度计的浊度值会停止增长，甚至会减小。有研究表明，海水电导率和悬沙浓度之间有着良好的负相关性[14-15]。本实验中当悬沙浓度小于1 g/L 时，悬沙浓度（S） 与浊度值（T）有很好的线性关系，相关系数平方R2达到0.99 以上（图2（a）至图2（c））。而当悬沙浓度大于1 g/L时，悬沙浓度与浊度值之间的线性关系减弱，但是电导率（C） 和悬沙浓度（S） 之间表现出很好的线性关系，相关系数平方R2达到0.95 以上（图2（d）至图2（f））。因此，本文中，将浊度计测量结果转换为悬沙浓度结果时，当悬沙浓度小于1 g/L 时，使用浊度值反演悬沙浓度，而当悬浮沙浓度大于1 g/L 时，则使用电导率反演水体悬沙浓度。最终，使用图2 中的线性关系，将1.1 节静水实验中测量获得的浊度值或电导率全部转换成悬沙浓度结果，最终得到3 个层位静水沉降过程中悬沙浓度时间序列结果。

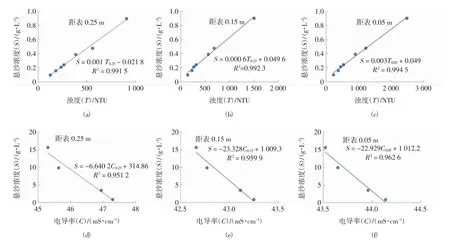
图2 悬沙浓度标定结果

1.3 泥沙沉降速度计算理论

取一个微元体（图3），假定其长度为△x，高度为△z，厚度为1，垂向上泥沙沉降量梯度可以表示为∂（ωS）/∂z。坐标系设置z 轴垂直向上，x 轴水平。在△t 时间内，进入微元体内的泥沙质量为，在重力作用下沉降离开微元体的泥沙质量为ωS△t△x，二者的差值为△t△x△z，这个差值表征着微元体内泥沙质量随时间的变化率，该变化率的直接数学计算公式为△t△x△z，由于质量守恒，并约去△t△x△z，则可以得到式（1）。

图3 二元水流中进出微元体的泥沙量

对公式（1）在垂向上进行空间积分，通过简单变换，同时规定沉降速度向下为正，可得到泥沙沉降速度表达式[16]。

2 实验结果

2.1 泥沙粒级分布特征

泥沙粒径对于沉降速度具有重要的影响。本次实验使用的泥沙样品来自废黄河口现场采集的海水水样中的悬浮泥沙。使用Mastersizer2000 激光粒度仪对水样中的沉积物进行粒度分析，结果显示，泥沙中值粒径为6.73 μm，全部由淤泥质组成，泥沙粒级分布概率曲线为单峰，粒度分选性较差（图4）。沉积物颗粒最大粒径不超过52.48 μm。

图4 泥沙样品粒度分布特征图

2.2 悬沙浓度结果

通过标定实验，我们得到了静水实验过程中3个层位水体悬沙浓度随时间变化的情况（图5（a））。结果显示，实验开始时，悬浮泥沙基本均匀分布于水体中，悬沙浓度为15.8～19.4 g/L。随着时间的推移，上层（距表0.05 m） 和中层（距表0.15 m） 两个层位的悬沙浓度持续降低；而底层（距表0.25 m）位置的悬沙浓度，随着时间推移先增加最大值达到37 g/L，在约10 min 之后，悬沙浓度开始快速下降（图5（a））。实验结果说明，悬浮泥沙在距表0.25 m层位产生了聚集，表现为开始的悬沙浓度升高。吴宋仁[17]于2008年在沉降筒实验中同样观察到，当初始悬沙浓度超过某个临界值之后，泥沙在静水条件下自然沉降，数分钟之后在某一层位会出现明显的清浑水交界面，之后，浑水界面将缓慢下沉，这和本实验中观测到的底部悬沙聚集现象相吻合。图5（b）展示了悬沙浓度随时间的变化率（∂S/∂t），结果显示当悬沙浓度在5～8 g/L 时，3 个层位的悬沙浓度时间变化率均出现了一个峰值（0.042 g/（L·s-1））；对于距表0.05 m 和0.15 m 两个层位，当悬沙浓度小于5 g/L 时，悬沙浓度时间变化率随着悬沙浓度的增加而增加，而当悬沙浓度大于8 g/L 时，悬沙浓度时间变化率随着悬沙浓度的增加而减小。

图5 静水沉降实验中3 个层位悬沙浓度随时间变化情况

2.3 沉降速度计算结果

使用式（2）分别计算3 个层位悬浮泥沙沉降速度，计算结果显示，悬浮泥沙的沉降速度极大地受到悬沙浓度的影响（图6）。当悬沙浓度在1.5～2.5 g/L 时，悬沙的沉降速度达到峰值（约2 mm/s），而当悬沙浓度小于1.5 g/L 时，悬沙沉降速度随着悬沙浓度的增加而增加，而当悬沙浓度大于2.5 g/L时，悬沙沉降速度随着悬沙浓度的增加而减小，说明发生了沉降阻碍效应。对于细颗粒泥沙，随着悬沙浓度增加，泥沙发生絮凝，使得沉降速度增加；然而，当悬沙浓度超过某个临界值以后，随着悬沙浓度的增加，絮凝体之间的空隙进一步减小直至近似或者小于絮凝体本身尺寸，此时絮凝体相互影响并阻碍沉降，导致整体的泥沙沉降速度下降，这种现象被称为沉降阻碍效应。3 个层位的悬沙沉降速度与悬沙浓度之间的对应关系十分接近，这在一定程度上说明本实验结果的可靠性。实验结果能够反映样品采集区域悬浮泥沙沉降速度特征，对于评估样品采集区域的沉积动力过程具有重要的参考价值。

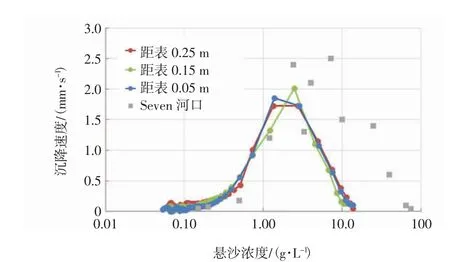
图6 沉降速度和悬沙浓度关系

3 讨 论

3.1 静水沉降实验及泥沙沉降速度评估

细颗粒泥沙在静水中的沉降一般可以分为4 个阶段[17]：①悬沙浓度较低时的絮凝沉降阶段，在该阶段絮凝作用导致泥沙颗粒链接成絮团，泥沙沉降速度增加；②悬沙浓度超过一定数值后的阻碍沉降阶段，在该阶段絮团进一步胶结在一起形成更大的规模，它们之间相互影响导致沉降速度下降；③含沙量进一步增大后的群体沉降阶段，在该阶段絮团之间形成具有一定刚性的网架结构，泥沙颗粒之间保持一种近似稳定的状态，沉降速度大幅降低，在本实验开始的几分钟内，最底层悬沙浓度增加，并在达到30 g/L 左右时，保持着约5 min 的基本稳定，正属于这一情况；④密实阶段，该阶段絮团网架结构之间的孔隙水受挤压排出，沉降速度很小，泥沙处于固结阶段。阻碍沉降效应对于沉积物运动、物质输运和沉积过程都有着重要的影响，其通常发生于悬沙浓度在2～10 g/L[18]，和本实验结果及Severn河口的数据相吻合（图6）。本次实验中观测到了细颗粒泥沙在静水中沉降的前3 个阶段，最后的固结阶段，由于没有对桶底沉积物进行测量，则未有数据记录。本次针对高悬沙浓度静水条件下的沉降实验过程和前人的观测结果基本吻合，表明实验过程是可靠的。

本实验分析计算泥沙沉降速度所依据的原理和重复深度吸管法[14]的计算原理相同（式（2））。在实际实验操作中，垂向上仅仅布置了3 个仪器，导致数值积分计算时存在一定的误差，也即垂向悬沙测量的分辨率越高，计算的结果将越加准确，但是需要更多的悬沙浓度测量仪器。本文中不同水层的悬沙浓度使用光学浊度计测量获得，以避免直接采样过程对静水沉降过程的干扰，遗憾的是在高悬沙浓度时期，浊度超出浊度计的量程，进而使用电导率来进行悬沙浓度反演，由于电导率的精度不足，导致计算结果存在误差。实验开始时，悬沙理论上应该均匀分布，然而3 个层位的结果保持在15.8～19.4 g/L 范围，产生的误差最大约12%。此外查看浊度计仪器标准，得到浊度计浊度误差最大不超过5%。将这些误差带入式（2），综合推算得到实验中分析计算获得地泥沙沉降速度极限误差在40%以内。对于重复深度吸管法，需要通过抽吸方法获得测量层位水样，并对水样进行过滤获得其悬沙浓度，实验装置复杂，且采样过程会影响泥沙沉降过程，导致无法获得准确实验结果。对比而言，本实验方法更加简洁实用，实验快捷。通过实验计算获得的沉降速度表征的是泥沙颗粒群体沉降速度，这个数值可以直接用于沉积动力模型分析。

3.2 絮凝对沉降速度影响

本文介绍的评估泥沙沉降速度的实验主要研究细颗粒黏性泥沙的群体沉降速度，导致沉降速度复杂化的机理主要是细颗粒泥沙的絮凝现象。MIKKELSEN O 等[19]和WINTERWERP J C[20]依据Stokes 理论总结出了针对絮凝体的沉降速度经验公式ΔρgMZ2/（18 μ），其中，Δρ 为絮凝体有效密度，MZ是絮凝体直径，g 为重力加速度，μ 为水体动力黏滞系数。然而，由于泥沙粒径、含盐量、水温、悬沙浓度及湍流等因素均对絮凝过程有不可忽略的影响，因此，絮凝体的有效密度和絮凝直径等参数，目前还没有通用的理论公式可以对其进行计算[18]。

相对来说，含盐量和温度对沉降速度的影响较小[21]，而且海洋里面的盐度和温度的时空变化相对平缓。而悬沙浓度和湍流结构由于受到周期性的潮流和风浪等动力影响，在短时期内就可能有很大的变化，在空间上也有很大差异，尤其是近岸海域。湍流涡旋最小尺度，科尔莫戈罗夫尺度（Kolmogorov Scale）[22]，其计算公式为（ν3/ε）1/4，其中，ν 为水体分子黏滞系数，ε 为湍流耗散率，控制着絮凝体的最大尺度：当絮凝体的尺寸大于这个参数时，湍流剪切会破坏絮凝体结构，而当絮凝尺寸小于这一尺度时，絮凝体则会被湍流涡旋聚集在涡内[4，23]。另一个重要的研究湍流对絮凝影响的参数是耗散参数（G），计算公式为（ε/ν）1/2，该参数是湍流耗散率的函数[24]。MANNING A J 等[25]于1999年的研究表明沉积物絮凝体平均尺寸和G-m成正比，其中，指数m 在悬沙浓度为0.08～0.20 g/L 时，数值为0.47～1.29；WANG Y P 等[4]于2013年在九龙江口进行了现场观测，通过统计分析得出絮凝体平均尺寸与悬沙浓度和G 均存在负相关关系。

悬沙浓度对悬浮泥沙沉降速度的影响也有很多研究。当悬沙浓度较低时，沉降速度可以表示为γSn，其中，γ 和n 是经验参数。而当悬沙浓度较高时，沉降速度则表示为（1-S）m，其中，m 是经验参数。SOULSBY R L 等[18]在2000年依据大量实验数据，给出了一个通用的泥沙沉降速度和悬沙浓度之间的经验计算公式。然而，对于不同的研究区域，以上经验公式中的参数并不相同，仍然需要通过实验方法来确定。总体来说，细颗粒沉积物中的泥沙颗粒的沉降速度评估主要依据半理论半经验公式，目前为止还没有适用于所有区域的准确且通用的计算方法，公式中很多的参数具有地域特性，因此对于细颗粒泥沙的沉降速度评估，尤其是将室内试验结果推广到自然环境条件下，还有很多工作需要完成。

4 结论

本文介绍了一种简单便捷地在室内实验室评估细颗粒沉积物群体沉降速度的实验方法。针对现场采集的细颗粒悬浮泥沙样品，通过简单的室内静水沉降实验，使用光学浊度计测量悬沙浓度，进而通过数学分析计算获得泥沙沉降速度，同时评估沉降速度与悬沙浓度之间的关系，实验结果较为准确可靠，能够为数值模型和沉积过程分析提供准确的参数。

在本文的实验中，测量了3 个层位的悬沙浓度随时间的变化结果，通过理论分析和数学计算，分别得到了3 个层位泥沙沉降速度与悬沙浓度之间的关系，计算结果比较接近，说明实验结果可靠。实验结果显示，当悬沙浓度小于1.5 g/L 时，随着悬沙浓度的增加，沉降速度快速增加，最大值约为2 mm/s，接着随着悬沙浓度的进一步增加超过2.5 g/L时，沉降速度开始随着悬沙浓度地增加而减小，当悬沙浓度达到14g/L 时，沉降速度下降至约0.16mm/s。该实验给出了细颗粒黏性沉积物中的泥沙颗粒群体沉降速度与悬沙浓度之间的对应关系，可以直接表征研究区域的泥沙沉降速度特征。实验方法比较简单、便捷，易于在室内实现，能够极大提高沉积物沉降速度评估效率和准确度。

本文仅仅评估了悬沙浓度和沉降速度的关系。然而，研究表明，水动力条件，尤其是湍流结构会影响细颗粒泥沙的絮凝过程，进而影响泥沙沉降速度。这是本文静水实验中没有考虑的因素，也是我们后期将要进一步研究的内容。