基于蚁群算法的物流多任务分配中路径规划研究*
金梦圆,王勇畅,刘敬琪
(西北工业大学计算机学院,陕西 西安 710129)
0 引言
自2013年以来,国家大力推进“一带一路”发展理念,不断加大电商业务发展的支持力度[1],且随着社会分工和服务的不断精细化,“懒人经济”成为消费升级的衍生产物[2]。在电商与懒人经济的双重推动作用下,我国快递行业的业务量呈逐年上升的趋势,从2013 年的1441.7 亿元上升至2021 年的10332.3 亿元[3]。2019~2021 年分别为7497.8 亿元、8795.4 亿元、10332.3 亿元。同期全国GDP 数据分别为98.65 万亿、101.36 万亿、114.37 万亿。由此可以计算出快递业务量分别占GDP 总量的0.76%、0.87%和0.90%,占比呈上升趋势。可见快递业务对于方便人们生活的重要性。因此,如何设计好上门收货的最短路线问题对于快递行业的发展、提升社会生产效率有着重要意义。
事实上,路径优化许多学者已经做了大量的研究工作[4-9],不过已有的工作未能考虑到多任务下可能出现在某一任务中存在孤立点的情况。孤立点的存在使得路径的计算更加复杂,本文试图借助其他任务中的收货点使得路径计算变得简单一些。
1 问题描述
某公司有五位快递员C1~C5负责上门收货,有八个仓库W1~W8用于临时存放所收货物,所收货物位于200个收货点R1~R200,仓库及收货点位置如图1所示。现在公司有20 个任务单A1~A20,每个任务单包括收货点编号,快递员先到某个仓库领取任务单,然后到任务单上每件货物对应收货点收取货物,收完该任务对应货物后再到某个仓库交回收取的货物,待完成该任务后才能领取下一任务。
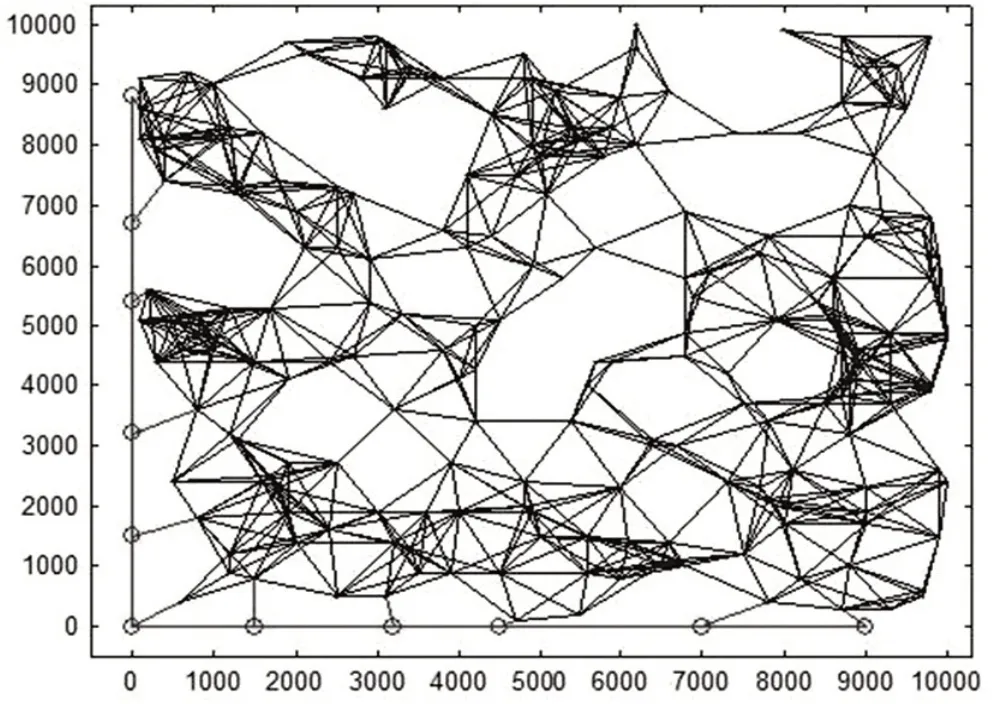
图1 仓库及收货点位置
图1 中红色的圆圈代表仓库,蓝色的点代表收货点,仓库与仓库之间、仓库与收货点之间、收货点与收货点之间的连线,表示两点之间可以直接通达,否则表示不能直接通达。
为了解决上述问题,我们建立如下数学模型:
模型一若快递员C1从仓库W1领取任务单A1,完成任务A1后可回到任意一个仓库交货,建立模型求解最优路线;
模型二若W1~W4四个仓库可使用,快递员C1需要完成任务A1~A4共四个任务,并自行确定每次领取任务的仓库和交货的仓库,在模型一的基础上求解最优路线;
模型三若八个仓库W1~W8都可使用,快递员C1~C5共需要完成任务A1~A20共20 个任务,在模型二的基础上求解最优路线。
对于这三个模型,本文利用Floyd 算法计算两点之间最优距离,用蚁群算法求解任务路径最优解。
2 算法简介
2.1 Floyd算法
Floyd 算法是在给定的加权图中计算多个源点之间最短路径[10]。本文利用Floyd算法进行数据预处理,求出模型一的任务单A1中的收货点和m 个仓库所有位置点中任一两点之间的最短路径,为后续利用蚁群算法求解任务最优解决方案提供基础。
文中使用Dis(i,j)表示收货点i 到收货点j 的最短路径的距离。计算任意两个收货点i、(ji≠j)的之间的距离有以下两种可能。
⑴直接计算两个收货点之间的欧几里得距离。如果收货点i 可以直接到达收货点j,则可以利用两点位置坐标关系进行计算;如果收货点i 不能直接到达收货点j,则可以定义Dis(i,j)=∞。
⑵间接计算。从收货点i经过若干个其他收货点k(k≠i,j,k∈S,其中S为不包括收货点i、j 的所有收货点集合)到达收货点j,此种情况,需要分别计算Dis(i,k)和Dis(k,j),判断
是否成立,如果不成立,证明收货点i 直接到达收货点j之间的距离为最优距离;否则,令
表明从收货点i 经收货点k 再到收货点j 的路径比从收货点i直接到收货点j的路径更优。每执行一次式⑴的判断,则将k从S中删除,当S为空时,则Dis(i,j)的值便是收货点i和收货点j两点之间的最优距离。
通过Floyd 算法可算得模型一中任一两收货点之间和收货点与仓库之间存在的最短路径,通过蚁群算法可得到遍历所有收货点的最短总距离。由于所有收货点以及仓库点之间有连线的距离为这两点的欧几里得距离,故可根据两位置点的横纵坐标表示两点之间的距离:
2.2 蚁群算法
蚁群算法在求解旅行商问题、指派问题、调度问题、图着色问题和网络路由问题等方面获得广泛的应用。实践证明,蚁群算法具有鲁棒性强、收敛性好等特点,是解决上述问题的一种非常实用的优化算法[11]。
蚁群算法模拟蚂蚁在寻找食物源时,会在沿途释放一种分泌物——信息素,同时能够感知其他蚂蚁在附近释放的信息素。路径的远近可以通过信息素的浓度值来表示,信息素浓度越高,表示蚂蚁离信息素源越近,即对应的路径越短。通常,蚂蚁会以较大的概率选择信息素浓度较高的路径,同时,为了使其他蚂蚁也最大可能选择同样的路径,该蚂蚁会释放一定量的信息素以增强该路径上的信息素浓度。另外,信息素浓度也会随着时间的流逝而逐渐减少。
不失一般性,设整个蚂蚁群体中蚂蚁的数量为m,收货点的数量为n,收货点i 与收货点j 之间的距离Dis(i,j)(i,j=1,2,3,…,n),t时刻,用τij(t)来表示收货点i与收货点j 之间的信息素浓度。任务开始时刻,假设各个收货点(包括仓库点)间连接路径上的信息素浓度相同,设τij(0)=τ0。
t 时刻,蚂蚁(即快递员)k(k=1,2,…,m)选择下一个收货点,是根据该时刻路径上的信息素浓度来决定的,设(t)表示t 时刻蚂蚁k 从收货点i 转移到收货点j的概率[12],其计算公式为:
其中,ηij(t)为启发函数,(其中Dij根据式⑶计算)表示蚂蚁从收货点i转移到收货点j的期望程度;allowk(k=1,2,…,n)为蚂蚁k待访问收货点的集合,开始时,allowk中有(n-1)个元素,即包括除了蚂蚁k出发站点的其他所有站点,随着任务进度的推进,allowk中的收货点不断减少。当所有收货点均访问完毕时,allowk为空;α为信息素重要程度因子,其值越大,表示信息素的浓度在转移中起的作用越大;β为启发函数重要程度因子,其值越大,表示启发函数在转移中的作用越大,即蚂蚁会以较大的概率转移到距离短的收货点。
由蚁群算法思想可知,在蚂蚁释放信息素的同时,各个收货点间连接路径上的信息素也在逐渐消失,设参数ρ(0<ρ<1) 表示信息素的挥发程度。因此,当所有蚂蚁完成一次循环后,各个收货点间连接路径上的信息素浓度需进行实时更新。
其中,Q为常数,表示蚂蚁循环一次所释放的信息素总量,Lk为第k个快递员经过路径的长度。
3 实验数据
针对前述模型一,取任务单号A1作为研究对象,其中的货物收取点和所有仓库的位置关系如图2所示。图2 中的连线表示收货点与收货点、收货点与仓库之间可以直接通达。
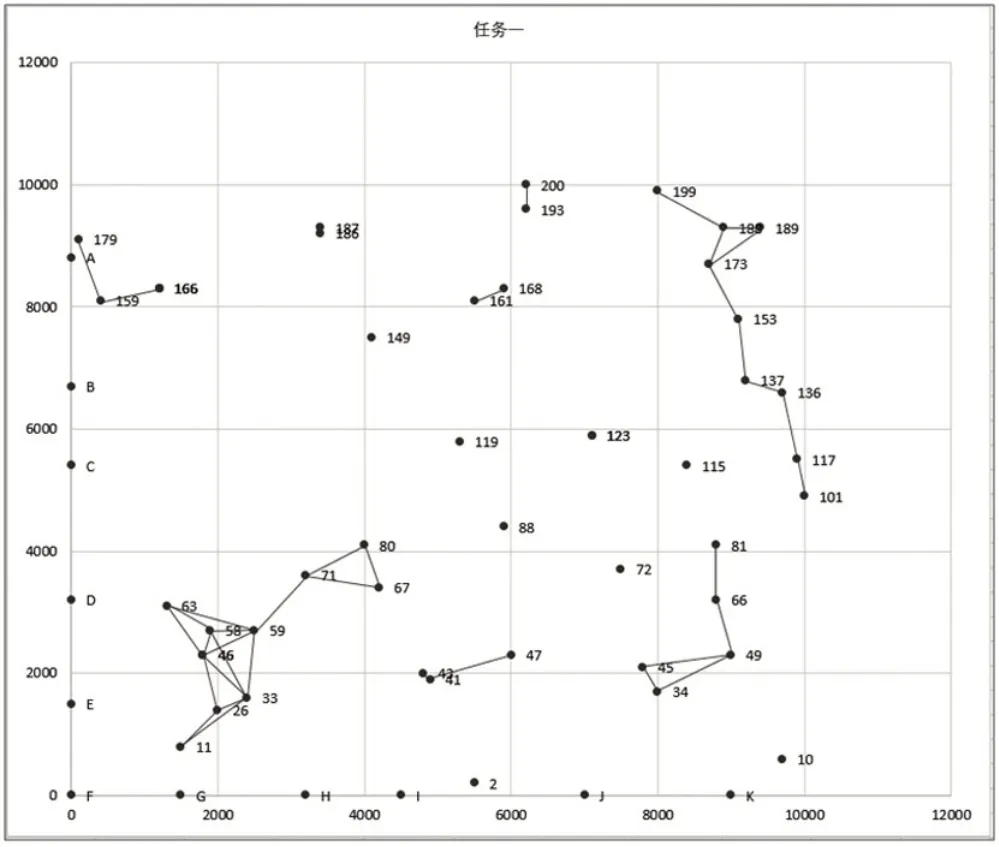
图2 任务单号1收货点及仓库位置图
由图2可以看出,在任务A1存在许多孤立点,这是和其他学者研究的不同之处。由图1 可以看出,这些孤立点可以借助该任务之外其他收货点间接到达任务A1中的其他收货点。所求得路径和路径长度如表1所示。
针对模型二,在模型一的基础上进一步对模型二进行求解。由于模型二中的出发点和终止点在本研究中未做要求,故在模型一的基础上结合动态规划进行一定的修改,可求得执行第i 个任务(i=1,2,3,4)的最短路径。
模型二中的任务单号、任务单对应的收货点编号、路径和路径长度如表1 所示。表1 中路径中涉及到其他收货点,是由于存在收货点之间不能直接到达,借助于其他收货点间接到达。模型二中快递员C1接到4 个任务单,按照A4-A3-A2-A1顺序执行收货任务,可以缩短所走路径。

表1 实验数据
针对模型三,在模型二的基础上拓展至八个仓库可用,且需要五个快递员同时完成20个任务。对模型二进一步分析可知,快递员C1分配得到任务A1~A4即可得出领取任务的仓库点和交接货物的仓库点,以及执行任务的先后顺序,从而得出遍历所有收货点的路线图。其他快递员领取到对应的任务单后,以同样方法根据模型二进行处理,可以得出每个快递员的任务执行顺序和路线。
因篇幅所限,本文只给出了模型一、模型二中的实验数据,模型三数据与模型二类似。
4 结束语
实验数据表明,结合Floyd 算法和蚁群算法,可以快速有效地解决在多任务分配情况下的路径选择问题,为快递员提供最优的路径选择决策方案。此方法同样可以应用于机器人配送、无人机配送中路径选择决策场景中。

