FR-ICP算法在倾斜摄影测量点云配准中的应用
任镤 孙晓敏 李源 徐崇斌 王树辉
FR-ICP算法在倾斜摄影测量点云配准中的应用
任镤1孙晓敏2李源3徐崇斌2王树辉4
(1 北京印刷学院,北京 102600) (2 北京空间机电研究所,北京 100094) (3 西安博物院,西安 710054) (4 北京几何维度科技有限公司,北京 100162)
倾斜摄影测量技术在大场景三维重建应用中,需要通过多片点云数据的刚性配准来实现数据融合。传统迭代最近点(Iterative Closest Point,ICP)算法在实际应用中存在收敛速度慢、易受异常值影响、精度低等具体问题。文章将一种快速且鲁棒的ICP算法(FR-ICP)引入航空倾斜摄影测量应用领域,通过引入Welsch函数描述配准误差,提高缺失点云数据的配准精度;通过李代数形式表示变换矩阵,将优化求解过程转换为固定点迭代加速,大大提高了算法的收敛速度。在小雁塔真实测绘三维点云数据集上验证了算法有效性,实验结果表明FR-ICP算法可解决航空倾斜摄影在古建筑数字化保护应用中多源、大尺度海量点云数据融合处理问题,提高基于倾斜摄影测量重建三维点云的数据精度。
迭代最近点 倾斜摄影测量 三维点云 点云配准 遥感应用
0 引言
随着无人机和传感器硬件的发展,以及基于计算机视觉的图像三维重建技术的提高,无人机倾斜摄影测量技术已在许多领域取得广泛应用,改变了传统的航空摄影测量只能从垂直角度拍摄地物的局限性。完整的倾斜摄影系统通过在一台无人机上搭载多台摄像机和传感器,可以同时从垂直和侧视的不同角度采集数据,生成带有空间位置信息的高分辨率图像,进而在算法支持下实现目标表面的三维重建。目前,无人机倾斜摄影测量作为航空摄影测量应用中的重要技术手段,已经从科学研究阶段走向成熟的行业应用,成为我国航空遥感监测体系的重要补充。
利用航空倾斜摄影测量完成古建筑的三维数据采集,是遥感测绘技术在文化遗产数字化保护领域的重要应用。与二维遥感数据处理不同,三维数据采集要求测量系统完成地面目标在空间中的三维点云计算,这对测量系统整体的稳定性、拍摄图像分辨率和重复区域面积都有较高要求。由于中国古建筑体量大、结构复杂,且存在大量自遮挡等问题,实际作业中需要多次拍摄计算点云并进行配准[1]。此外,地面激光扫描(Terrestrial Laser Scanning,TLS)在古建筑数字化中可直接获取高精度的三维点云数据,但是在高空作业中应用受限。将高空倾斜摄影测量技术重建生成的三维点云与激光扫描点云进行配准融合,可大大提高数据的精度和完整度,目前已成为古建筑三维数字化的标准技术方案。其中,点云数据配准的鲁棒性和精确度将直接决定数据结果的质量。
在理想的刚性配准结果中,目标空间表面同一位置在不同点云中的采样位置应完全重合。为接近这个理想目标,文献[2]、[3]引入迭代优化思想,逐渐形成早期经典迭代最近点(Iterative Closest Point,ICP)算法。传统的ICP算法多采用二范数来描述配准误差,导致结果易受异常值和缺失数据的影响,收敛于局部最优。针对这些问题,许多学者从不同角度出发对算法提出了改进,如通过改进初始配准、改进收敛函数、改进点对搜索方式提高算法效率等[4]。考虑初始位置会影响ICP算法配准结果,许多研究通过粗配准,在计算点云对应阶段加入几何结构特征来提高初始配准精度,如:文献[5]利用SIFT特征检测计算特征点集,同时将特征融合在对应点的计算过程中,提高对应点搜索的准确性;文献[6]利用拐点特征实现点云数据降采样,提高ICP算法在大规模点云数据中的有效性;文献[7]提出GICP方法,通过计算高斯分布得到最优变换矩阵,提升算法对噪声和离群值的鲁棒性。为扩大算法收敛范围,文献[8]提出go-ICP算法,使用八叉树将初始空间细分为子空间,利用分支定界搜索满足条件的子空间找到全局最优变换,解决算法易收敛于局部极小值的问题。文献[9]提出MVGICP算法,在多尺度体素上计算均值和方差,再带入GICP模型中,提高了计算效率。为降低缺失数据和异常值的影响,文献[10]提出Sparse-ICP算法,通过定义度量函数降低远距离对应点的影响,提高配准精度,但是该方法求解速度低于传统ICP方法。文献[11]提出利用Anderson加速的AA-ICP算法,从改进收敛函数和搜索方式两方面提升算法效率。AA-ICP算法采用欧拉角作为刚性变换的参数化形式,将传统两步交替迭代的测量合并为一步固定点迭代,提出两种启发式策略来解决Anderson加速的不稳定性,提高点云配准的收敛速度和鲁棒性。最新工作中,文献[12]提出FR-ICP算法,用李代数代替欧拉角参数化刚性变换,并提出基于Welsch函数的点对点鲁棒距离度量,通过极大极小方法进行Anderson加速,从定义误差度量和改进迭代方式两方面提升了算法效果,相较其他改进ICP算法具有更高的精度、鲁棒性和效率。
已有ICP改进工作在标准数据集上提升了传统ICP算法的配准效果,但是在真实数据集中提升有限。利用倾斜摄影测量技术重建生成的三维点云通常存在点云数量多、体量大、噪声多等问题,与激光扫描数据配准时会出现数据重叠有限、缺失较多、尺度不一致等具体问题,传统配准方法很难得到准确的配准结果。实际工作中常采用半自动配准方法,在人工标定对应点基础上通过调用软件集成的配准功能来实现精确配准。本文为了解决倾斜摄影测量技术在古建筑三维点云配准中的具体应用问题,引入FR-ICP算法实现快速鲁棒的自动配准;针对激光扫描和重建点云多源异构数据的配准问题,通过一种近似内蕴体素的点云简化算法将两组点云降采样,在保留数据特征基础上计算变换矩阵。按照本文提出的算法对小雁塔古建筑三维点云数据进行了配准测试,验证结果显示该算法可有效提升倾斜摄影测量在三维重建应用中的点云配准精度和效率。
1 ICP算法模型

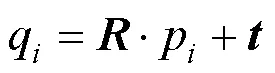

式中 (*,*)为变换后的旋转平移矩阵。
从以上求解过程可以看出,传统ICP算法利用L2距离作为度量函数,通过迭代计算源点云变换后与目标点云的最小二乘距离,实现距离最小化,最终实现配准。计算过程易受异常值影响而陷入局部最优,因此存在局限性。在倾斜摄影技术的大规模场景点云配准应用中,因点云数量巨大,导致噪声和异常值较多,且结构复杂,多源数据通常还会带来点云密度变化、重叠区域有限等问题。因此,实际应用中直接采用ICP算法及其他基于L2距离的改进算法,很难得到鲁棒高效的配准结果。
2 算法改进
2.1 数据预处理
传统ICP算法要求待配准点云数量严格一致,在实际问题中难以直接应用。而采用FR-ICP算法虽然可以大大提高配准的效率和精度,但是如果使用完整点云数据进行配准,计算量非常大,导致配准时间过长无法得到理想结果。本文首先通过对点云数据进行降采样预处理,减少配准过程的计算量[13]。来自真实世界的点云数据存在较大噪声,需要通过滤波算法去除噪声和异常点。本文采用一种基于体素结构的近似内蕴(Approximate Intrinsic Voxel Structure,AIVS)点云简化算法对数据进行预处理[14]。对于高分辨率扫描或重建生成的密集点云数据,体素越密集的地方有效信息越多,因此可通过体素网格去除离群点。AIVS算法利用点云数据的全局体素结构将简化任务分解为可并行处理的子任务集合,同时通过内蕴结构对点之间的距离进行控制,从而更好地保证原始数据的几何一致性。
此外,使用原始海量点云进行配准需要消耗大量计算和存储资源,因此在利用体素滤波器进行去噪的同时需要对原始点云进行降采样。利用AIVS算法在划分的体素中进行局部最远点采样,能够在保持点云全局分布密度的同时有效简化点云,在不破坏点云几何结构的同时获得低数据量表达。简化后的三维点云可以大幅减少异常点影响。
2.2 距离度量函数

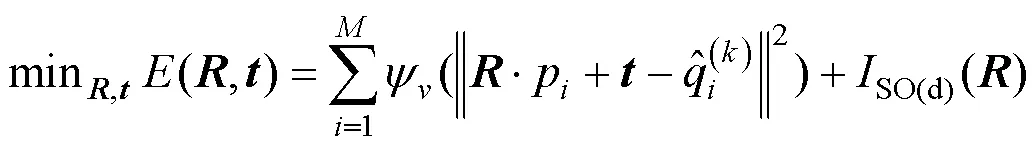
图1 不同参数对应的Welsch函数曲线
Fig.1 Welsch curves with different parameters
为了选取适当的Welsch函数参数值,FR-ICP算法采用动态调整方式,以达到自适应的求解刚性配准问题。考虑到初始位置时,直接计算源点云和目标点云之间的距离较近的最近点不准确,该算法采用由粗糙到精细的配准过程。将初始状态最近点之间的距离中值作为参数的初始值,目标函数迭代收敛时,减小参数值并继续迭代,直到达到或低于预设终止值,终止迭代。终止值由源点云和目标点云的密度决定。
2.3 收敛算法加速
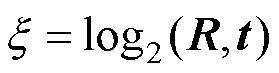
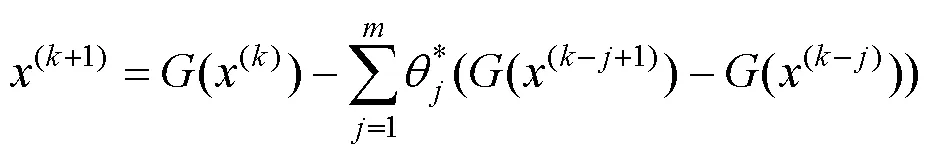

由于Anderson加速具有不稳定性,计算的加速解并不能保证距离度量函数值是降低的。文献[12]提出的FR-ICP算法采用一种简单的策略保证结果单调下降,即判断度量函数值是否降低,若降低则接受加速解,否则用加速前的解作为当前迭代最优解,然后继续迭代求解直到收敛。
3 实验与分析
3.1 数据描述
本文以小雁塔点云数据融合处理作为应用实例,来验证FR-ICP算法在倾斜摄影测量数据中应用的有效性。小雁塔位于陕西省西安市,作为中国唐代密檐式佛塔的典型代表,小雁塔古建筑三维数字化具有重要意义。小雁塔现存主体高43.4m,底层边长11.38m,高台基底座边长23.38m。小雁塔建筑体量大,顶部缺失,塔身表面细节丰富。为保证采集数据的完整性和高精度,利用航空倾斜摄影和地面激光扫描融合方法生成完整的古建筑外表面三维点云。扫描阶段,采用地面站式激光扫描仪FARO Focus Premium 350采集高精度三维点云,精度达0.2cm。航拍阶段,采用2台无人机规划不同路径围绕小雁塔采集空中影像,图像分辨率为5 472×3 648像素。实际采用大疆M300无人机搭载35mm定焦P1镜头,以及精灵4 RTX搭载24mm定焦镜头分别航飞完成高空作业。基于采集图像,利用ContextCapture软件实现空三测量,按照实验需求重建不同密度的三维点云。
待配准的小雁塔点云数据包含两种来源:一是地面激光雷达直接扫描生成点云,二是利用航空倾斜摄影测量技术重建生成点云。激光扫描采集生成的点云数量直接由扫描仪精度决定,实践中利用站式激光扫描仪对小雁塔地面部分进行多站扫描,融合生成包含超过1亿个三维点的原始点云。倾斜摄影测量数据来源于围绕塔身航拍采集的7 400幅、地面单反相机补拍1 700幅二维图像,重建生成同等数据量的大规模点云模型。此外为验证算法在不同数据上的鲁棒性,实验中将地面近景拍摄图像与航空倾斜摄影图像进行随机分组,生成具有较多异常点的真实重建三维点云,分别配准进行验证。为执行点云配准算法,预处理阶段对点云进行降采样处理。
3.2 相同来源点云数据配准
在基于Intel CORE i7处理器、16G Byte内存、Nvidia Quadro P600显卡、8G Byte显存的硬件环境,Windows 10操作系统及Visual Studio 2019提供的编译环境下,对配准结果进行了测试比较。采用衡量点云配准误差的常用指标均方根误差(Root Mean Square Error,RMSE)RMS,作为小雁塔点云配准结果精度评估的指标,即


图2 重建点云配准结果对比
Fig.2 Registering results of reconstructed point clouds
图2中第一组输入点云为随机选取不同航拍照片重建生成点云的配准结果,数据来源完全一致,且初始姿态相近,因此4种方法生成结果几乎一致,FR-ICP算法没有体现出明显的优势;后两组输入为无人机与地面近景拍摄重建点云结果,从直观的视觉效果上看,FR-ICP算法得到了更加合理的配准结果,明显解决了其他3种对比方法无法解决的配准问题。表1为三组数据的配准精度和配准时间的定量分析结果。表1中,FR-ICP算法在均方根误差上没有体现优势,原因在于点云相对缺失过大,RMS值有时不能准确反映配准;结合图2中第三组实验结果可知,由于地面拍摄角度限制,待配准点云中重叠部分相对较小,对比方法虽能收敛得到较低的均方根误差值,但实际上并未计算出合理的配准结果。在类似相对缺失很大的点云数据集上,FR-ICP算法仍然可以适用。从时间上分析,引入李代数表达的Anderson加速效果(Fast-ICP)明显优于其他算法。FR-ICP算法由于采用Welsch函数,导致配准时间略长,但是Anderson加速算法可提升计算效率,保证算法在合理时间范围内得到最优结果。

表1 重建点云配准精度和时间对比
3.3 不同来源点云数据配准
相较基于图像重建生成的完整点云,站式激光扫描仪采集点云仅能覆盖自地面向上的有限视角,因此待配准的两组点云数据存在缺失,这对算法鲁棒性提出很大挑战。对于不同来源的点云数据,传统ICP算法受初始状态影响非常大。为验证FR-ICP算法在真实场景下不完整点云配准中的性能,对地面激光扫描点云和航空倾斜摄影测量重建的点云数据进行了配准测试对比。实验中固定目标点云,对源点云进行不同程度的平移和旋转变换,验证配准算法的有效性和鲁棒性。图3为配准测试结果。其中蓝色点云为全部9 100幅图像重建生成的稠密点云,降采样后保留500 000个三维点,作为目标点云;橙色为激光扫描生成的稠密点云,降采样后也保留500 000个三维点,作为源点云。对待配准点云数据的初始位置和姿态进行调整,验证FR-ICP算法克服陷入局部最小的有效性。

图3 地面激光扫描与航空倾斜摄影测量重建点云配准结果
图3所示结果中,传统ICP算法均未计算出满足要求的配准结果(两组点云未完全重叠);AA-ICP算法相较传统ICP算法虽然理论上具有更快的解算速度,然而在本文实验中,其并未表现出明显优势,配准结果与传统ICP算法类似,消耗时间甚至更多;Fast-ICP算法在采用了Anderson加速优化后,在提高速度方面效果明显,且引入李代数表达,在配准精度方面也较传统ICP算法有较大提升,但仍未改变ICP算法容易陷入局部最优的结果,例如,图3第一组实验中,Fast-ICP算法的配准结果有明显的90°错位;FR-ICP算法从Welsch度量函数和Anderson解算加速两方面对ICP算法进行改进,其在点云配准应用实践中的鲁棒性大大提升。表2所示3组实验的定量分析中,结合度量函数和解算加速的FR-ICP算法对不同初始位置点云配准结果均能达到较高精度,虽然在时间上不是总能优于其他算法,但是算法在稳定性方面性能最优,更加适合实际应用需求。

表2 地面激光扫描与航空倾斜摄影测量重建点云配准精度和时间对比
实验中对地面采集图像重建点云和扫描点云进行了配准测试,图4所示为实验结果。其中橙色为激光扫描生成稠密点云,降采样后保留500 000个三维点,作为目标点云;绿色为地面拍摄1 700幅图像生成点云,含416 216个三维点,作为源点云。相较于完整重建点云,扫描点云和照片同样是缺失数据,不能覆盖小雁塔全部外形。但是由于拍摄角度接近,原始数据姿态几乎一致,因此几种对比算法基本能够得到视觉合理的配准结果,但是错位明显。由图4结果可见,FR-ICP算法在不同来源缺失数据配准中,相较其他几种对比算法依然能够获得更好的配准结果。

图4 扫描点云与地面图像重建点云配准结果
由于地面激光扫描设备造价昂贵,古建筑数字化实践工作中经常省略高精度激光扫描工作,完全依靠航空倾斜摄影测量结合地面近景测量来采集图像数据,重建生成三维点云。然而,若能借助激光扫描的高精度点云在重建阶段对图像进行标定,对于重建结果精度的提升将非常有帮助。实验中利用FR-ICP算法验证标定步骤在点云重建精度结果中的有效性,即对标定重建点云、未标定重建点云和扫描点云进行配准,图5为实验结果,其中蓝色点云为图像重建时利用少量激光扫描点云进行标定重建生成的完整点云,黄色点云为未标定完全利用图像生成的完整点云,红色点云为地面扫描生成的高精度点云。图5(a)为利用激光扫描数据标定重建生成的点云与扫描点云配准结果,视觉上可见两组点云完全重合,由于存在缺失,均方根误差不为0;图5(b)和图5(c)可直接说明未标定步骤对重建点云结果有影响,可见未标定点云尺度上略小于标定后重建结果,转换为物理尺度,误差接近10cm。通过对比结果可知,单纯利用倾斜摄影测量采集得到的图片来完成三维点云重建,相较结合地面激光扫描点云融合生成的重建点云误差明显。因此在对测绘精度要求较高的应用中,宜采用地空融合的点云生成方法。

图5 地空融合与倾斜摄影测量重建点云精度对比
4 结束语
结合航空倾斜摄影测量技术和地面激光扫描完成古建筑三维数字化采集,目前已是遗址遗存类文物数字化保护的标准方案。本文在倾斜摄影测量点云配准问题中,引入一种快速且鲁棒的FR-ICP算法,通过小雁塔古建筑三维点云数据的配准实验,对FR-ICP算法在实际应用中的性能进行测试,结果显示该方法相较传统方法得到了更加精确的配准结果。此外,本文通过对比点云精度,验证了地面激光扫描数据在重建点云精度方面的重要性。实验证明,FR-ICP算法能够对不同来源的点云数据进行鲁棒且高效的精确配准,克服了传统ICP算法对于数据预处理的严格限制,以及随机陷入局部最优的算法缺陷,在航空倾斜摄影数据处理的实践应用中具有重要作用。
[1] REN P, ZHOU M Q, DU G G, et al. 3D Scanning Modeling Method Application in Ancient City Reconstruction[C]// Proceedings of the International Conference on Optical and Photonic Engineering. Singapore: IEEE Press, 2015, 9524: 1-10
[2] BESL P J, MCKAY N D. A Method for Registration of 3D Shapes[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256.
[3] CHEN Y, MEDIONI G. Object Modeling by Registration of Multiple Range Images[J]. Image and Vision Computing, 1992, 10: 145-155
[4] 李建微, 占家旺. 三维点云配准方法研究进展[J]. 中国图象图形学报, 2022, 27(2): 349-367.
LI Jianwei, ZHAN Jiawang. Review on 3D point cloud registration method[J]. Journal of Image and Graphics, 2022, 27(2): 349-367. (in Chinese)
[5] ZHENG Z, YAN L, WANG J. LiDAR Point Cloud Registration Based on Improved ICP Method and SIFT Feature[C]// 2015 IEEE International Conference on Progress in Informatics and Computing (PIC). [S.l.]: IEEE, 2016.
[6] REN Y, ZHOU F C. A 3D Point Cloud Registration Algorithm Based on Feature Points[C]// Proceedings of the 1st International Conference on Information Sciences, Machinery, Materials and Energy. Chongqing, China: Atlantis Press, 2015: 802-806.
[7] SEGAL A, HHNEL D, THRUN S. Generalized-ICP[C]//Robotics: Science and Systems V, University of Washington, Seattle, USA, June 28 - July 1, 2009. [S.l.: s.n.], 2009.
[8] YANG J, LI H, JIA Y. Go-ICP: Solving 3D Registration Efficiently and Globally Optimally[C]//Proceedings of the 2013 IEEE International Conference on Computer Vision. [S.l.]: IEEE, 2013.
[9] LIU H, ZHANG Y, LEI L, et al. Hierarchical Optimization of 3D Point Cloud Registration[J]. Sensors, 2020, 20(23): 6999.
[10] BOUAZIZ S, TAGLIASACCHI A, PAULY M. Sparse Iterative Closest Point[J]. Computer Graphic Forum, 2013, 32(5): 113-123.
[11] PAVLOV A L, OVCHINNIKOV G V, DERBYSHEV D Y, et al. AA-ICP: Iterative Closest Point with Anderson Acceleration[C]//2018 IEEE International Conference on Robotics and Automation: ICRA 2018, Brisbane, Australia, 21-25 May, 2018. [S.l.: s.n.], 2018: 1-6.
[12] ZHANG Juyong, YAO Yuxin, DENG Bailin. Fast and Robust Iterative Closest Point[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 44(7): 3450-3466.
[13] PEREIRA N S, CARVALHO C R, THE G. Point Cloud Partitioning Approach for ICP Improvement[C]//2015 21st International Conference on Automation and Computing (ICAC), September 11-12, 2015, Glasgow, UK. [S.l.: s.n.], 2015.
[14] LYU Chenlei, Lin Weisi, ZHAO Baoquan. Approximate Intrinsic Voxel Structure for Point Cloud Simplification[J]. IEEE Transactions on Image Processing, 2021, 30: 7241-7255.
Application of the FR-ICP Algorithm in Point Cloud Registration of Tilt Photogrammetry Technology
REN Pu1SUN Xiaomin2LI Yuan3XU Chongbin2WANG Shuhui4
(1 Beijing Institute of Graphic Communication, Beijing 102600, China)(2 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)(3 Xi’an Museum, Xi’an 710054, China)(4 Beijing Geometric Dimension Technology Co., Ltd, Beijing 100162, China)
In the application of tilted photogrammetry technique in the large-scale 3D reconstruction, it is necessary to conduct the rigid registration of multiple point cloud data to realize the data fusion. The traditional Interative Closest Point(ICP) algorithm has some problems in practical application, such as slow convergence speed, easy to be affected by outliers and low accuracy. FR-ICP algorithm introduced Welsch function to describe the registration error, which can significantly improve the registration accuracy of missing point cloud data. Meanwhile, the FR-ICP algorithm represents the transformation matrix by Lie algebra form, and the convergence speed of the algorithm is greatly improved based on fixed point iteration acceleration. Experimental results show that the FR-ICP algorithm can improve the data accuracy of 3D point cloud reconstruction based on tilt photogrammetry. By utilizing the FR-ICP algorithm, we can solve the problem of multi-source and large-scale massive point cloud data fusion processing in practical applications, especially for the digital protection of Chinese ancient architectures.
iterative closest point;tilted photogrammetry; 3D point cloud; point cloud registration; remote sensing application
TP399
A
1009-8518(2023)01-0013-10
10.3969/j.issn.1009-8518.2023.01.002
2022-12-13
北京市自然科学基金(4214064);北京印刷学院校级项目(Eb202308)
任镤, 孙晓敏, 李源, 等. FR-ICP算法在倾斜摄影测量点云配准中的应用[J]. 航天返回与遥感, 2023, 44(1): 13-22.
REN Pu, SUN Xiaomin, LI Yuan, et al. Application of the FR-ICP Algorithm in Point Cloud Registration of Tilt Photogrammetry Technology[J]. Spacecraft Recovery & Remote Sensing, 2023, 44(1): 13-22. (in Chinese)
任镤,女,1989年生,2019年获北京师范大学计算机应用技术专业博士学位,现为北京印刷学院讲师,中国图形图象学会会员。主要研究方向为几何建模、文化遗产数字化保护。E-mail:renpu@bigc.edu.cn。
(编辑:夏淑密)

