复杂非水密结构目标强度预报方法研究

赵欣阳， 梅志远， 祝 熠， 杜 度

(1.中国人民解放军海军工程大学 舰船与海洋学院，武汉 430000；2.中国人民解放军92578部队，北京 100000)

潜艇声隐身技术一直备受关注，数十年减振降噪工程技术的发展使得各国在潜艇声辐射控制领域取得了长足进步，严重削弱了传统被动声呐的探测性能。而主动声呐具有探测低噪声甚至“无声”目标的优势，因而得到重视。20世纪70年代初，声学覆盖层的引入使得潜艇在声目标强度控制技术方面有了显著提高，但也带来了一系列问题，此结构不似传统金属结构，其内部细观特征复杂，材料性质多样，以往的用于传统金属材料的声目标强度预报方法已不再完全适用。此外，目前对于潜艇声目标强度的研究大多集中在外壳方面，当然对于潜艇大部分结构来讲，一般不需要考虑声波透射进入内部的情况，但对于潜艇非水密结构却必须区别对待。此结构整体被水所填充，仅有一部分升降通路为耐压结构可视为刚性壳体。这意味着声波入射到结构上时，外壳不可被视为刚性，必定会有大量声波透射进入内部。由于潜艇内部存在挡板、肋骨以及各种管道，声波便会在多种结构之间产生复杂的声散射，散射声场不可控，极有可能出现一些未知“亮点”， 所以对于这样非水密结构的目标强度预报也显得尤为重要。

声目标强度预报的实质便是求解水下目标的声散射问题，即求解目标在声激励作用下的散射声场，目前该问题的解决方法主要分为理论与数值计算两部分。理论研究方法主要有积分方程法[1]与简正级数法[2]两种，数值计算方法可分为以Helmholtz表面积分方程为基础发展起来的边界元法[3]、有限元结合边界元法[4]、无限空间中的有限元法[5]、T矩阵方法[6]与波叠加方法[7]等等。这些方法在解决简单结构方面各具优势，针对性也不尽相同，但均在处理含复杂内部结构的声学覆盖层时存在较大阻力。在处理此结构时，有限元法虽能对其进行建模，但在离散整个结构过程中会造成网格数量巨大，计算代价极高。为研究声学覆盖层的声学特性，参数反演是一种很好的思路。Schneider等[8]将超声波法用在测定固体弹性常数上，利用板中的纵波与横波测量了几种金属的弹性常数。陶猛等[9]运用模拟退火算法，联立多层平板结构反射系数计算传递矩阵，反演得到了消声瓦结构的等效反射系数。孙铁林等[10]基于遗传算法，利用水下覆盖粘弹性板的回波实验，反演得到了复合板的相速度、衰减系数与弹性模量。金国梁等[11]利用遗传算法对复杂声学覆盖层进行了参数反演以得到其等效参数，在利用等效参数进行圆柱壳体声散射计算时发现等效后结构与原有复杂结构的声散射形态函数基本吻合。周世根[12]分别采用等效刚度均匀化方法与参数反演法提取了内部含圆柱型空腔与圆锥形空腔的等效材料参数，研究结果表明，在利用等效材料进行声目标强度计算时，壳体内部介质为空气时利用此方法更好。

目前参数反演方法在对声管试验亦或是无限大平板仿真反演中基本能达到较好的效果，但在运用到圆柱壳亦或是其他结构上却精度不高，这是由两方面原因所造成的，一是所采用的优化算法较为单一，存在一定的局限性；二是考虑不足，未考虑斜入射以及声波透过结构后的多次散射问题。本文针对以上问题，结合现行不同算法的优势，在考虑斜入射、多次散射、吻合效应以及横波波速阈值的情况下利用分层介质理论构建了双层弹性介质层反演模型，此模型可替代原有敷设声学覆盖层的复杂模型，为非水密结构声目标强度预报提供了一种有效的方法。

1 数学物理模型

1.1 模型描述

潜艇在结构设计上可分为耐压结构与非耐压结构，耐压结构主要包括潜艇的主体结构，如耐压船体、耐压指挥室等等；非耐压结构则可分为非耐压水密结构与非耐压非水密结构，前者主要包括主压载水舱、燃油压载水舱等，后者主要由上层建筑和指挥室围壳等结构构成，本文重点讨论的对象是非耐压非水密结构。对潜艇来讲，声波从外部入射时，以空气为背衬的耐压壳结构使得外壳结构内外的特性阻抗失配，声波几乎无法透射到结构内部，更不会对内部结构产生影响。但对于围壳与上建这样的非水密结构，外壳内外特性阻抗一致，声波透过外壳直接进入内部，在内部结构间形成复杂的声散射，从而对整体的回波产生贡献。

为真实模拟表面敷设声学覆盖层的潜艇非水密结构实际特征，同时提高仿真计算的效率，本文构建了如图1所示的无限长围壳模型。截面为椭圆型的围壳浸没在无限大水域中，a和b分别代表围壳的长轴半径与短轴半径，围壳内部由几个圆柱形耐压容器构成，外壳与耐压容器间充满水，在图1所示的坐标系下，内部耐压装置的位置与尺寸信息如表1所示。同时，围壳外壳材料为钢，表面敷设了声学覆盖层，局部放大结构如图1右侧所示，h1代表钢外壳厚度，h2代表声学覆盖层厚度，h3代表空腔底部到钢外壳距离，h4代表空腔高度，d代表空腔直径，围壳及声学覆盖层的几何参数如表2所示。

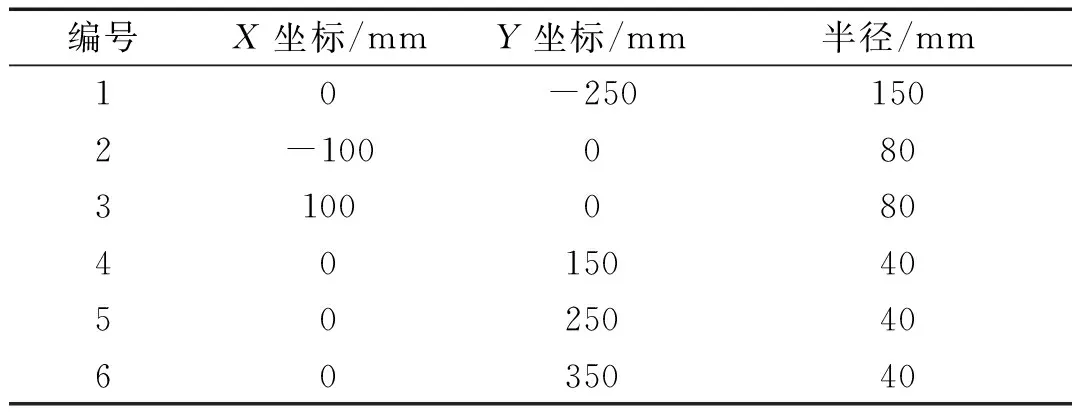
表1 内部耐压装置位置与尺寸信息Tab.1 Position and size information of internal voltage resistance equipment

表2 围壳及声学覆盖层几何参数Tab.2 Geometric parameters of submarine sails and acoustic coating

图1 无限长围壳模型(横截面)Fig.1 Infinitely long submarine sails model (cross section view)

1.2 理论基础

在本文所构建的模型基础上，想要通过反演手段得到与原结构目标强度一致的等效结构就必须认识到非水密结构的特殊性，即声波从声学覆盖层一侧入射与从钢板一侧入射时两者反射系数与透射系数存在差异。这时如果采用单层均质材料等效整个复杂结构则无法达到外侧入射与内侧入射反射系数与透射系数不一致的效果，这里引入考虑损耗的分层介质波理论解决此问题，通过构建双层不同材料的弹性介质层达到声波从两侧分别入射时反射系数与透射系数不一致的效果。

固态分层介质中的弹性波实际上就是一套递推公式的运用，这其中考虑了纵波与横波在固体中的折射与反射，以双层固态分层介质为例进行理论推导。如图2所示，当平面波从1侧入射时， 利用场在分界面的连续性条件可以得到1、2界面与2、3界面、2、3界面与3、4界面的速度关系，如式(1)所示。

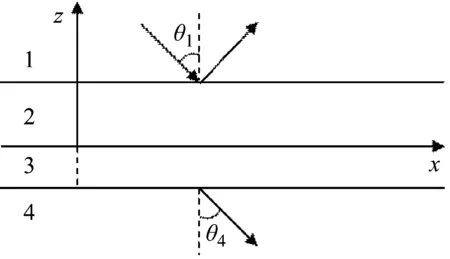
图2 声波在双层弹性介质层中的反射与透射Fig.2 Reflection and transmission of sound waves in double elastic dielectric layers

(1)

式中，a11,…，a44由固体介质中的纵波波速c、纵波折射角θ、纵波在厚度上的相移P、横波波速b、横波折射角γ、横波在厚度上的相移Q以及密度ρ组成。c与b可由杨氏模量E、密度ρ与泊松比σ决定，如式(2)所示。

(2)

当考虑材料损耗η后，杨氏模量就变为了式

E′=E(1+iη)

(3)

将层与层之间的速度关系建立联系，可直接得到整个层系的速度关系

(4)

当介质1与4是液体时，切向应力消失，借助连续性条件便可得到层系的反射系数V与透射系数D如式(5)和式(6)所示。

(5)

(6)

当从介质4侧入射时，只需调换矩阵[a(2)][a(3)]的位置，便可得到对应的反射系数与透射系数。为了模拟无限大双层弹性介质层，在COMSOL中建立如图3所示模型，第一层材料为聚氨酯声学材料，第二层材料为PVC材料，厚度分别为40 mm、10 mm，两层弹性介质层两侧流体为水，材料参数如表3所示。

表3 材料参数Tab.3 Material parameters

图3 无限大双层弹性介质有限元模型Fig.3 Finite element model of infinite double-layer elastic medium

水域两端设置完美匹配层以模拟无限远水域，在两层弹性介质层与水域的上下表面与左右表面分别设置Floquet周期性条件用以模拟无限大双层弹性介质层与水域。平面波以0°～80°入射到聚氨酯一侧或PVC一侧，入射频率为1～5 kHz，步长为1 kHz。

图4中的点为根据理论得到的结果，蓝线表示仿真结果。从图4可以看出，在考虑损耗后，利用分层介质波推导的声学理论解与无限大双层弹性介质层仿真解完全一致，也就意味着用于之后的声学系数计算是可靠的。

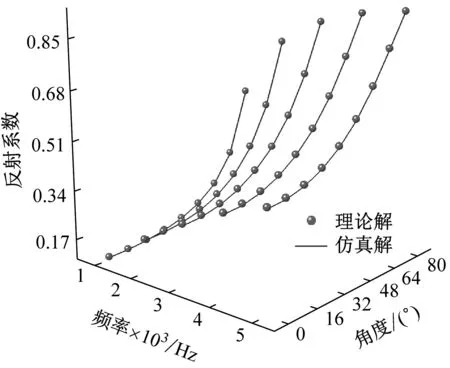
(a) 反射系数理论解与仿真值对比(聚氨酯一侧入射)

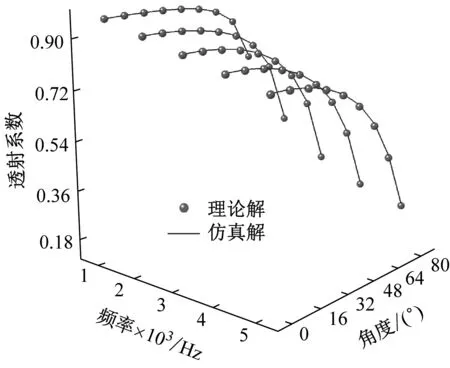
(b) 透射系数理论解与仿真值对比(聚氨酯一侧入射)

(c) 反射系数理论解与仿真值对比(PVC一侧入射)

(d) 透射系数理论解与仿真值对比(PVC一侧入射)图4 声学系数理论解与仿真解的对比Fig.4 Comparison between theoretical solution and simulation solution of acoustic coefficient

2 反演算法

2.1 优化措施

目前声学参数反演多采用遗传算法寻找最优解，遗传算法的本质是一种并行、高效的全局搜索手段，其通过自适应寻优手段得到最优解。现有的仅依靠遗传算法反演声学参数的手段基本能够满足正入射下简单周期结构的求解但在个别频率下仍存在较大误差，这是因为遗传算法在求解过程中重点关注全局寻找最优解，对于局部重视不够。为解决这部分存在的问题，考虑在遗传算法中加入非线性规划，将非线性规划的局部强搜索能力与遗传算法的全局强搜索能力结合在一起，从而提升寻找全局最优解的能力。

遗传算法的基础步骤主要分为六步，依次为种群初始化、适应度函数选择、选择运算、交叉运算、变异运算与终止条件判断，在本问题的寻优过程中会存在陷入局部最优解、效率不高、约束考虑不足等问题，对应这些问题，本文提出了对应的解决措施。

(1) 初始化种群的选择，反演声学参数的种群容易在模量的选择上出现问题，如果模量的范围上选取过大，譬如从104～1012，会使得模量在随机的过程中倾向于设定的上限，从而使得寻优过程中陷入次优解而达不到目标，一种方法是主动降低模量设定的上限，使得模量在随机的过程中更加均匀地分布在整个范围空间，但是这种方法需要人为估计，具有一定的经验性。另一种思路比较简单，就是在随机过程中将模量做一些预处理，将模量取对数后再进行随机，随机完成后再将预处理的模量取10次方得到模量的真实值进行求解。

(2) 适应度函数的选择，本小节的目的是通过对主要参数的调整使得反演后的等效结构能够达到复杂结构的声学特征，表征上就是优化后结构的反射系数与透射系数能够达到与复杂结构的反射系数与透射系数一致的水平，所以可设定式(7)作为适应度函数，那么本节的目的就转化成了求函数最小值的问题，函数值越小的个体，适应度值越小，个体越优。

abs(abs(Vij)-Rij))

(7)

式中:Dij、Vij为考虑损耗后推导出来的双层无限大弹性介质声学系数;Tij、Rij为复杂结构仿真或试验得到的声学系数。i从1取到9，分别对应入射角0°～80°时的情况，j从1取到2，分别对应声学覆盖层一侧入射与钢板一侧入射的情况。

(3) 非线性规划，措施(1)与(2)是针对本文问题以及利用遗传算法反演声学参数过程中易存在的问题提出的解决措施，基本能够满足寻优要求，但在个别频率下仍存在较大误差，这是因为遗传算法在求解过程中重点关注全局寻找最优解，对于局部重视不够，所以需非线性规划来加强局部最优解的求取。要想在遗传算法中引入非线性规划，首先需要对适应度函数做处理，将适应度函数通过数学上的变换使其可以求导，这样可以加快非线性规划寻找极值的速度，那么适应度函数的形式就变为了式(8)所示。

(8)

非线性规划的核心就是研究一个多元函数在无约束或者多约束下的极值问题，经典的非线性规划算法采用梯度下降的方法求解，局部搜索能力强，且收敛速度加快。

(4) 约束考虑

为了保证反演过程的收敛性，遗传算法与非线性规划相结合的组合算法在种群初始化阶段与进化阶段均对参数设置了范围约束，如将材料1和材料2的杨氏模量E范围设为104～1012，泊松比σ设置为0.01～0.499，损耗因子η设置为0.01～4，密度ρ设置为1 000～10 000 kg/m3，反演介质1的厚度范围为10～40 mm、反演介质2与反演介质1的总厚度为50 mm，这其中并不考虑等效后各个参数的真实意义。但若想仿真结果与理论结果完全吻合，还需做进一步的约束处理，本文重点考虑横波临界波速与吻合效应。

① 横波临界波速的判定

本文对种群材料参数的范围设置较广，目的是在较大范围内使得适应度值尽可能小，从而寻得最优解，但这样的处理会使得两种反演介质的横波与纵波波速不可控，很可能出现波速极小的情况。以两种波中速度较小的横波为例，当其速度小于5 m/s时，在5 000 Hz的情况下，固体介质的网格尺寸就必须控制在0.2 mm以内才能满足精度要求(声学计算时网格尺寸需小于五分之一波长)。这样的网格尺寸会使得仿真计算量激增，达不到大幅提高计算效率的目的，所以需对反演材料每个频率下的横波波速设定一个阈值。因此，本文利用式(9)对反演材料进行判定，仅保留符合条件(9)的种群，从而在满足网格精度要求的基础上最大化提高仿真计算效率。

(abs(b)/5f)≥5 mm

(9)

式中：b代表横波波速；f代表频率。

② 吻合效应临界频率的判定

借助分层介质波理论得到无限大平板的透射系数后，会存在一种较为特殊的情况，即如果板周围液体的阻抗远小于板的阻抗，那么在入射波沿板的径迹速度与板中自由波的相速度一致时，则会发生全透射。利用分层介质波理论去求解无限大双层弹性介质的全透射条件过于困难，这里从胀缩波与弯曲波的角度去理解这个现象。平面波入射到平板上时，当液体中的声波在板上的投影与板的弯曲波吻合，声波便会激发板的固有振动，使得结构的声辐射能力大大增强，这种现象叫做吻合效应。当板在一定条件下产生了吻合效应，板将强烈振动，透射系数显著变化，此时有限元仿真所得到的声学系数将难以与理论解吻合，从而导致反演结果不准确。所以为了避免反演材料在所研究的频段内产生吻合效应，本文引入了王鹏伟等[13]所提出的“等效薄板法”用以判定吻合效应的产生与否。

利用经典层合板理论得到如图5所示的层合板弯曲刚度计算公式为

图5 层合板弯曲刚度示意图Fig.5 Schematic diagram of bending stiffness of laminated plate

(10)

程序主要流程图如图6所示。首先进行系统初始化,完成MCU,ESP8266,传感器模块以及电源模块的初始化配置。ESP8266设置为STA模式,接入无线AP实现与主控制器的WIFI连接,将单片机置为LMP3模式,关闭MCLK与SMCLK时钟,仅开启ACLK作为串口模块时钟。当接收到开始采集指令后,触发串口中断,激活CPU,执行中断服务程序,进行数据采集与AD转换与无线发送,数据发送完成后开启定时器中断,当120 s内没有收到采集命令,结束本次采集,进入待机模式等待下一次采集。

(11)

式中：m为薄板的面密度；c为薄板两侧介质声速。利用式(11)对每个频率下的反演材料进行判定，仅保留设置频率小于吻合效应临界频率的种群，从而使得反演材料在所研究的频段无法产生吻合效应。

2.2 方案对比

为体现预处理后加入非线性规划的遗传算法的优势，制定三种方案进行对比，方案一为遗传算法，方案二为对模量预处理后的遗传算法，方案三在方案二的基础上加入了非线性规划，此外，所有方案中均对吻合效应临界频率与横波临界波速进行判定，遗传算法的参数选择如表4所示。

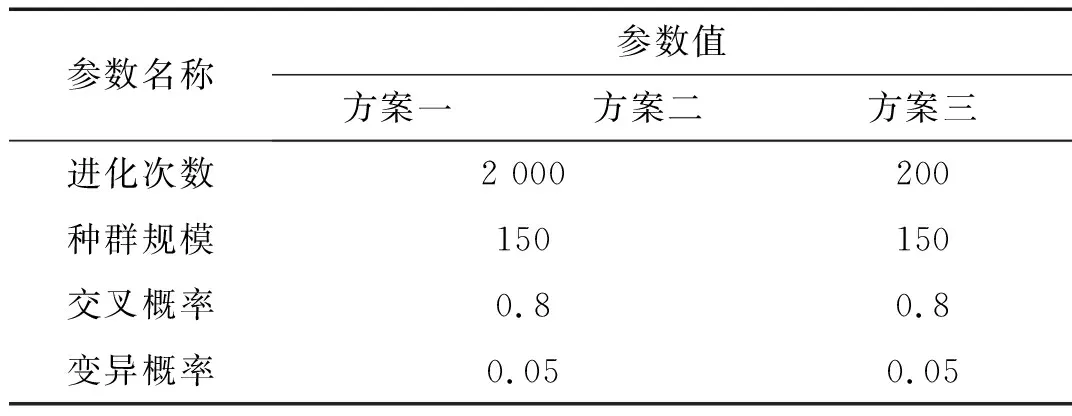
表4 各方案中遗传算法的主要参数设置Tab.4 Main parameter setting of genetic algorithm in each scheme

适应度函数中囊括复杂结构的仿真值，所以需要构建无限大样品用以提取声学系数，此部分依托于COMSOL有限元仿真平台。利用含圆柱空腔的钢背衬周期单元模拟无限大样品结构，如图6所示。

图6 圆柱形空腔单元模型Fig.6 Cylindrical cavity element model

基体、钢板与水的材料参数如表5所示，水域两端设置完美匹配层以模拟无限远水域，在结构与水域的上下表面与左右表面分别设置Floquet周期性条件用以模拟无限大样品与水域。平面波以0°～80°入射到覆盖层一侧或钢一侧，入射频率为1～10 kHz，步长为1 kHz。将有限元软件中提取的声学系数与三型方案反演的声学系数展示图7中。

(a) 反射系数(覆盖层一侧入射)

(b) 透射系数幅值(覆盖层一侧入射)

(c) 反射系数幅值(钢板一侧入射)

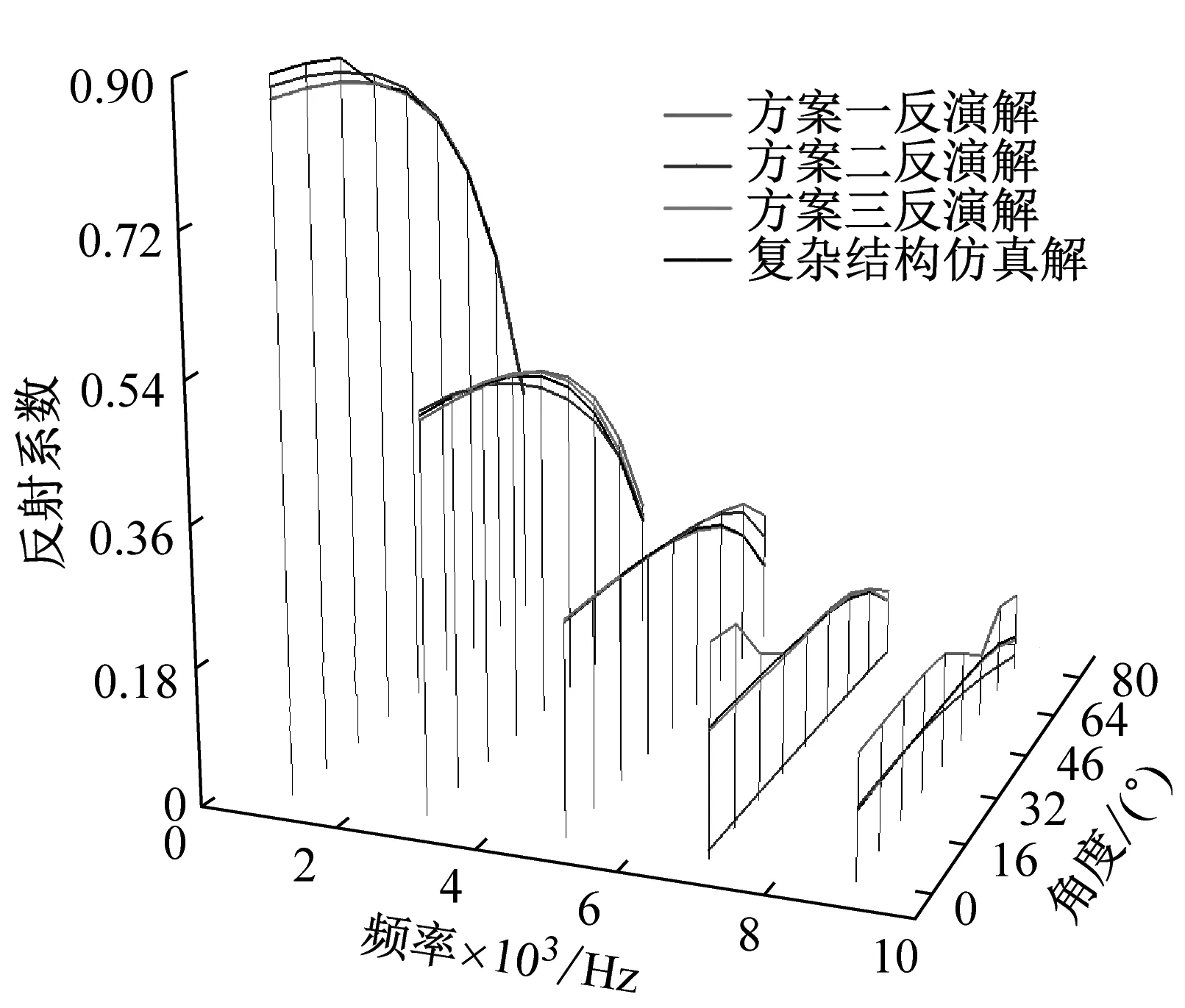
(d) 透射系数幅值(钢板一侧入射)图7 各种方案反演解与复杂结构仿真解的对比Fig.7 Comparison between inversion solutions of various schemes and simulation solutions of complex structures

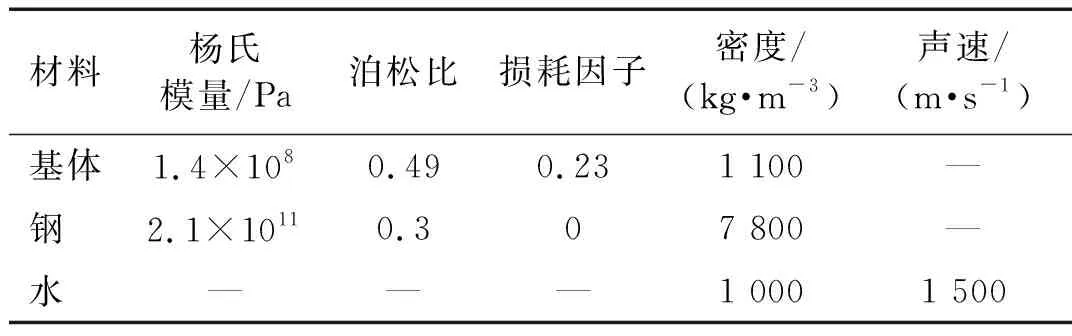
表5 材料参数Tab.5 Material parameters

从图7中可以看出，在加入吻合效应临界频率与横波临界波速的判定后，三种方案均能在一定程度上反演出复杂结构的声学特征，但明显方案三具有显著优势，反演出来的声学系数无论是从覆盖层一侧入射来看还是从钢板一侧入射来看都与复杂结构仿真解基本吻合，方案二虽较方案一在反演准确性上有一定的提高，但在部分频率与部分角度下仍存在较大偏差。此外，加入了非线性规划后的遗传算法可以大幅提高收敛速度，在收敛速度与求解结果上都优于基本的遗传算法。

3 非水密结构目标强度计算

3.1 数值计算模型有效性验证

为验证有限元方法计算水下结构目标强度的有效性，将基于COMSOL软件的数值仿真结果与无限长弹性圆柱简正级数解进行对比。模型如图8所示，主要参数包括:① 圆柱体半径为25 mm，弹性模量E=7×1010,密度ρ=7 800 kg/m3,泊松σ=0.33。② 水域外边界设完美匹配层，用于吸收入射波，模型无限大水域。平面声波正入射，频率为1～300 kHz，步长取1 kHz。根据入射波和散射波计算目标强度

图8 无限长圆柱有限元模型Fig.8 Finite element model of an infinitely long cylindrical cylinder

(12)

式中：ps表示距离目标r处的散射声压;pi表示入射声压，测量点选在反向散射处。对于无限长弹性圆柱，在正入射情况下，其入射声压与散射声压为

Pi=P0expi(kx-ωt)

(13)

(14)

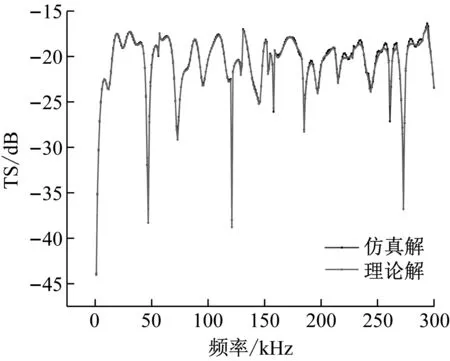
图9 无限长铝制圆柱体的目标强度Fig.9 The target strength of an infinitely long aluminum cylinder

3.2 模型建立

为验证本文构建的参数反演方法用于非水密结构声目标强度预报的可行性，按照无限大围壳模型构建了大小相同内部结构一致的反演模型，如图10所示。此外，考虑到围壳的介质环境与反演模型的介质环境需保持一致，计算时采用如图11所示的三维有限元模型。在图11所示的三维模型中，在水域与固体的边界上均施加Floquet周期性条件以模拟无限长围壳模型与无限大水域，在水域外侧设置PML层来形成无反射边界条件。

图10 反演模型Fig.10 Inversion model

图11 敷设声学覆盖层的围壳三维模型Fig.11 Three dimensional model of submarine sails with acoustic coating

3.3 参数反演结果

由仿真得到敷设声学覆盖层钢板的声学系数，利用方案三对结构进行等效参数反演，部分结果如图12所示。从图中可以看出，两种反演介质的材料参数随频率无明显的规律可循，总体来看，反演介质1的杨氏模量与损耗因子均较反演介质2稳定。

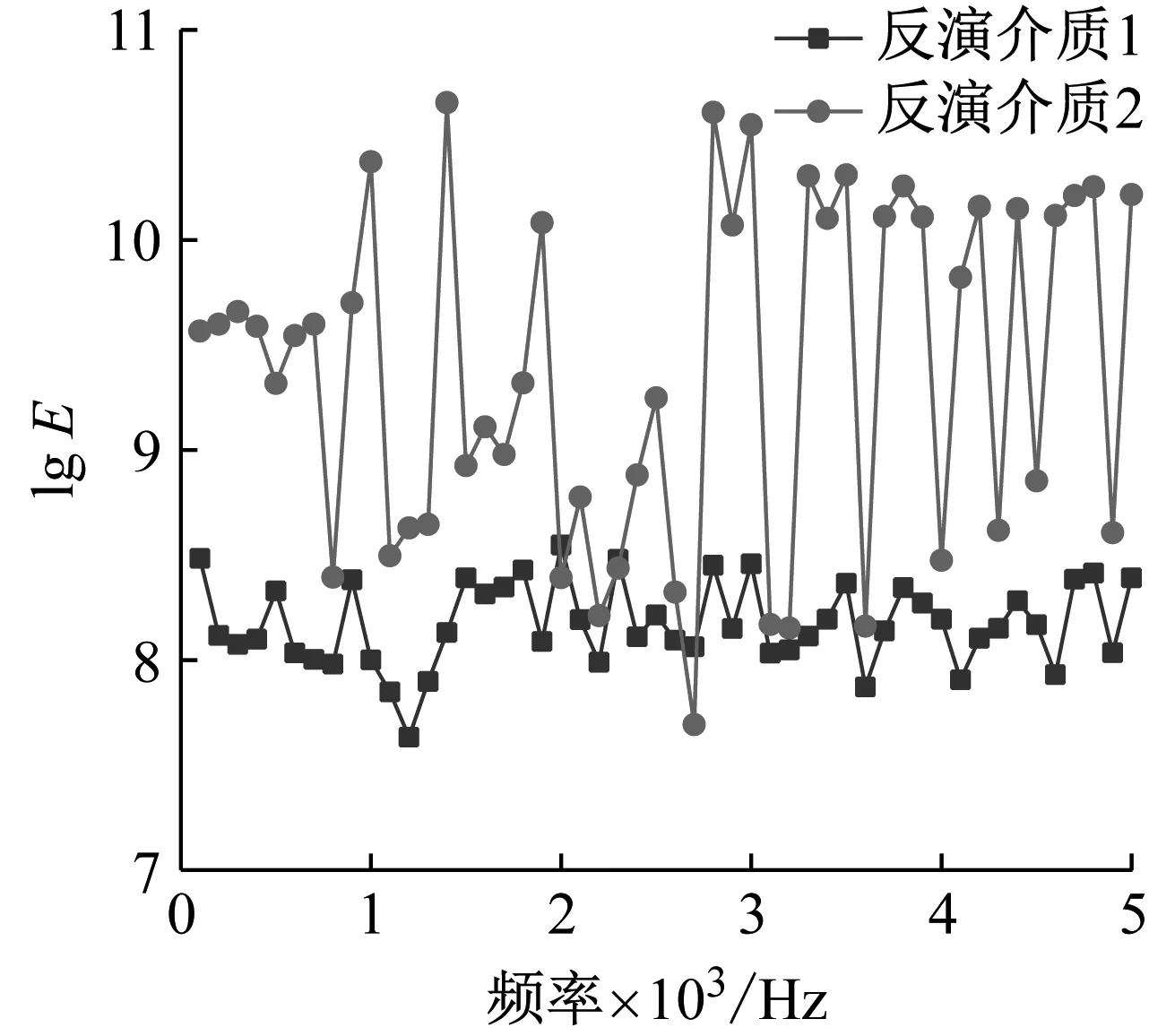
(a) 杨氏模量(取对数)

(b) 损耗因子

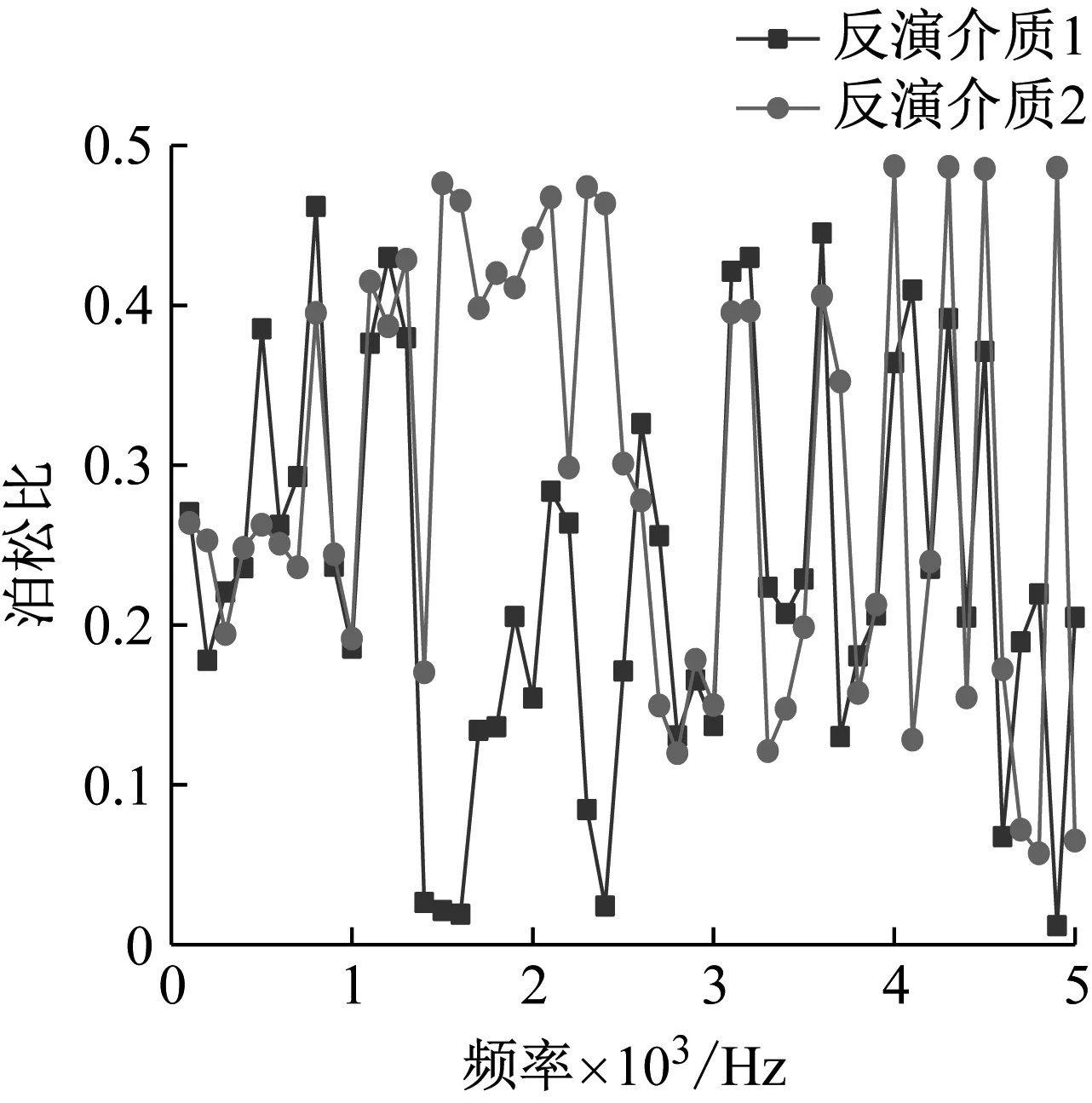
(c) 泊松比图12 双层弹性介质层参数反演结果Fig.12 Inversion results of parameters of double-layer elastic medium

3.4 目标强度对比

为充分验证本文构建的反演模型的准确性，在真实模型与反演模型的对比阶段选取了x方向入射、y方向入射与45°方向入射三种入射角度，每种入射角度拾取反向、30°两个方向的声目标强度值用以对比，入射频率从100 Hz到5 kHz，步长为100 Hz。

如图13所示，红线代表原结构的计算结果、黑线代表等效结构的计算结果。从图中可以看出无论从哪个方向入射，在收发合置的情况下，原结构与等效结构的各个频率下的目标强度值基本一致，仅在1 000～2 000 Hz频段内等效结构的目标强度较原结构有些许浮动，x方向入射、y方向入射与45°方向入射时研究频段的整体误差分别为1.25 dB，1.19 dB与1.28 dB。在30°收发分置的情况下，原结构与等效结构的各个频率下的目标强度值波峰波谷的趋势相同，x方向入射、y方向入射与45°方向入射时研究频段的整体误差分别为2 dB，1.30 dB与1.75 dB。

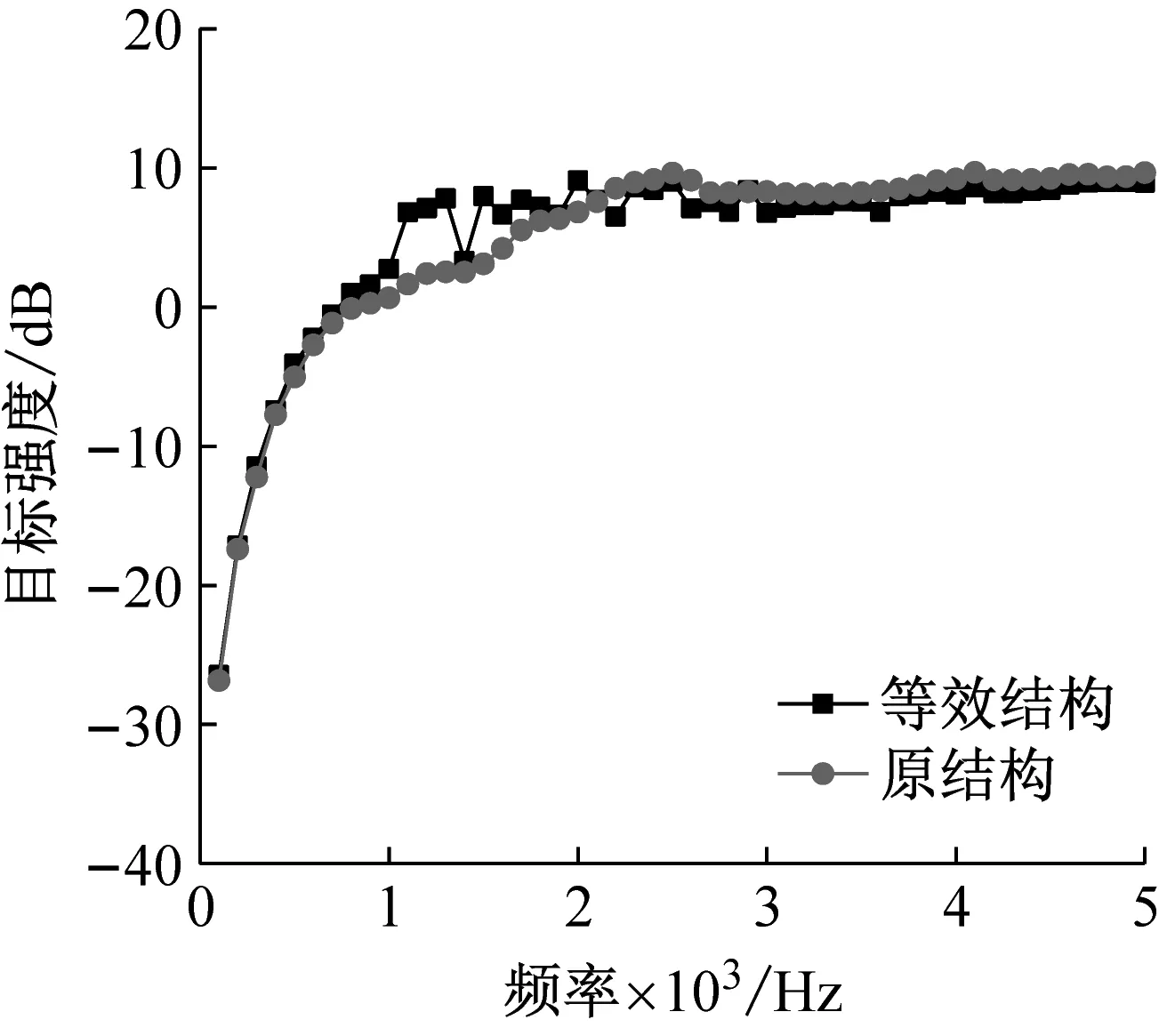
(a) 收发合置(x方向入射)

(b) 30°收发分置(x方向入射)

(c) 收发合置(y方向入射)

(d) 30°收发分置(y方向入射)

(e) 收发合置(45°方向入射)

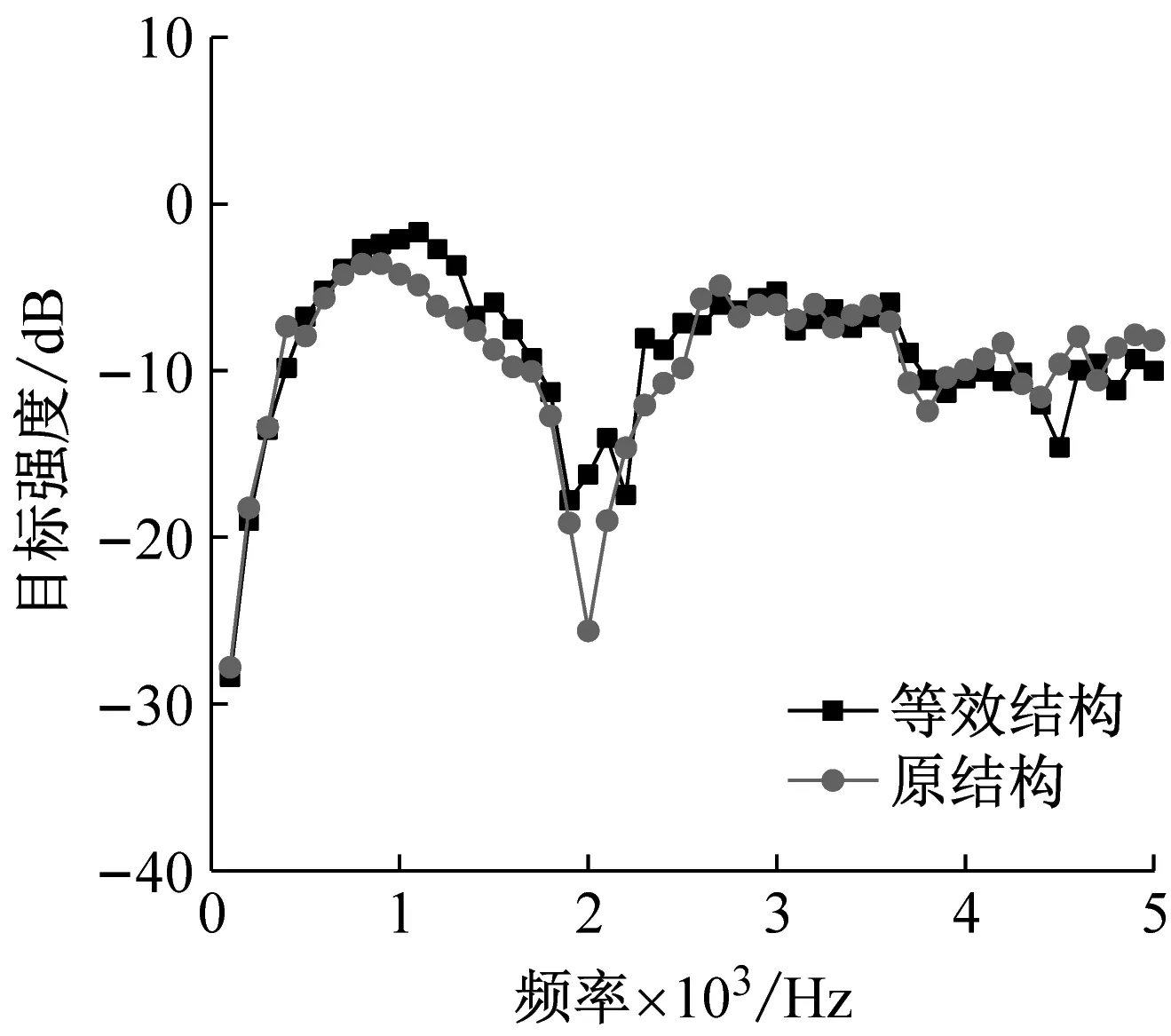
(f) 30°收发分置(45°方向入射)图13 目标强度计算结果对比Fig.13 Comparison of target strength calculation results

同时，图14给出了几个频率下原结构与等效结构的目标强度指向性对比。从图14(a)～14(b)可以看出，低频段等效结构与原结构指向性基本一致，但幅值存在一定差异。从图14(c)～14(e)可以看出，在1 000～1 600 Hz频段，等效结构与原结构在-30°～30°指向性一致，但幅值存在差异，尤其是1 200 Hz时，差异达到5 dB左右，这与此频率下反演结果与原结构吻合程度不高有关。从图14(f)～14(i)可以看出，随着频率的增加，原结构与等效结构目标强度一致性越来越高，且在-30°～30°范围内，此频段的目标强度基本一致。总体来看，-30°～30°范围内，除个别频率外，原结构与等效结构目标强度基本吻合。

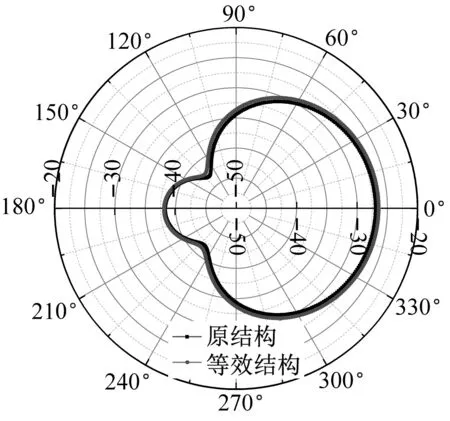
(a) 100 Hz

(b) 600 Hz

(c) 1 000 Hz

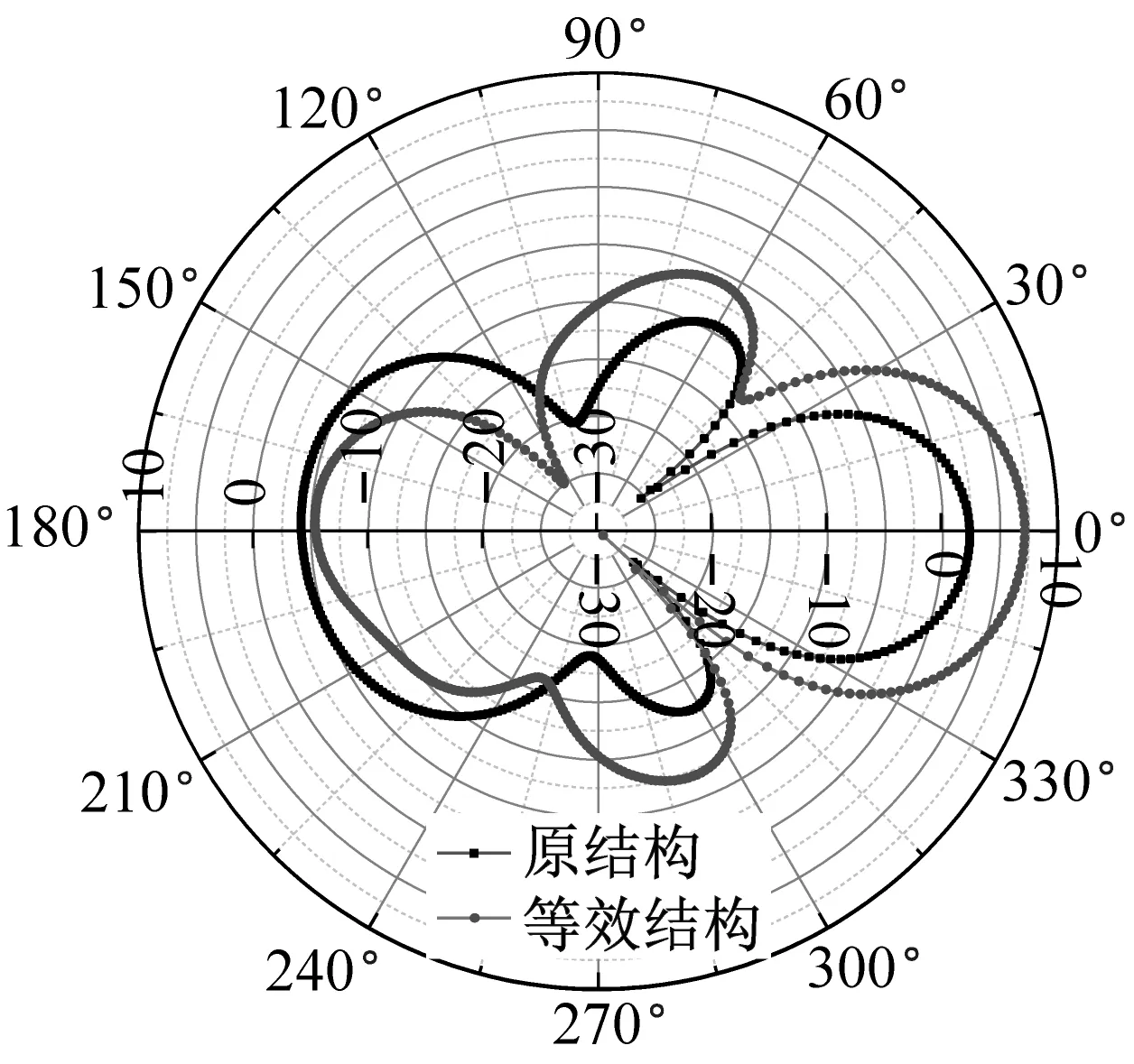
(d) 1 200 Hz

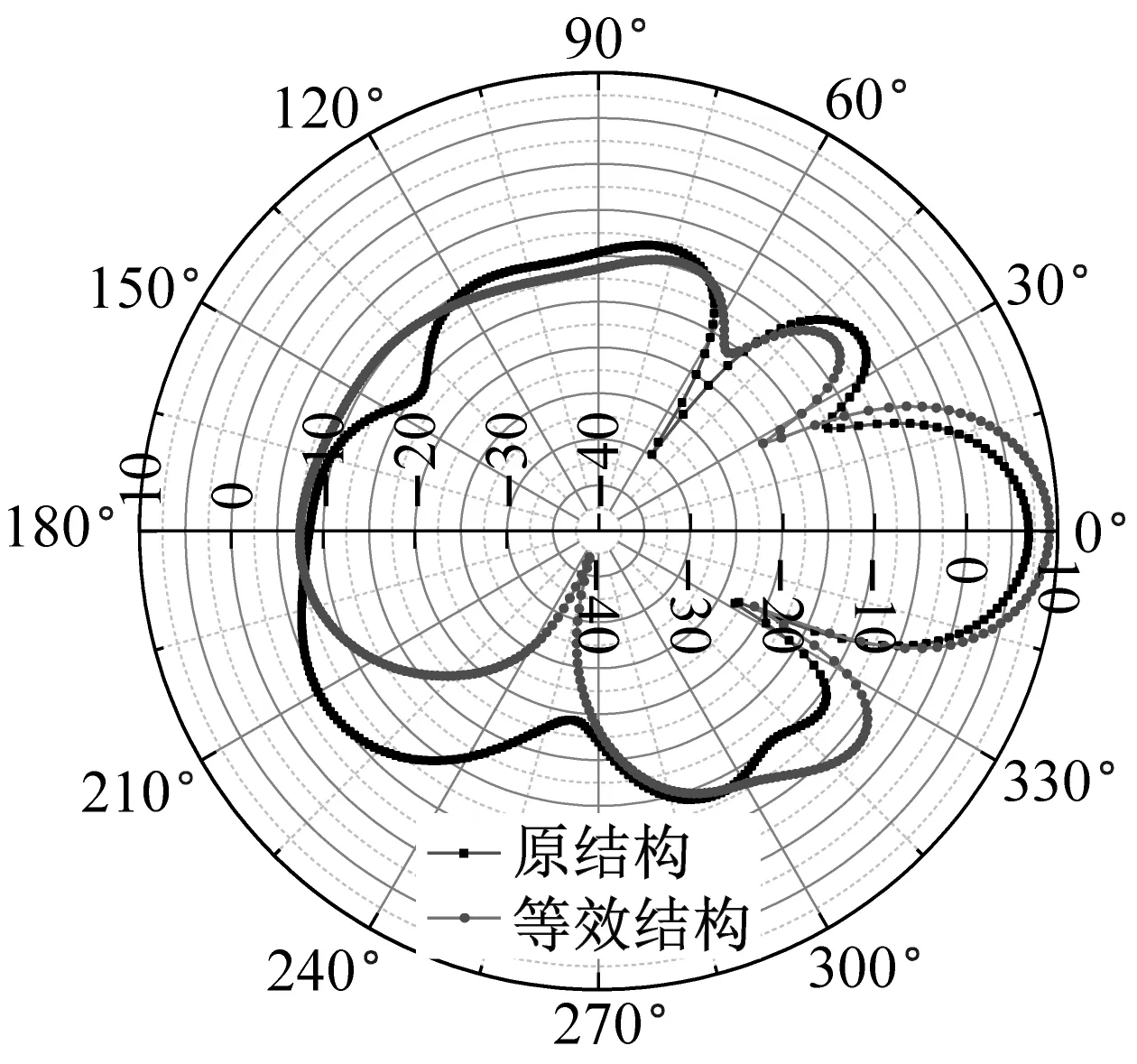
(e) 1 600 Hz

(f) 2 000 Hz

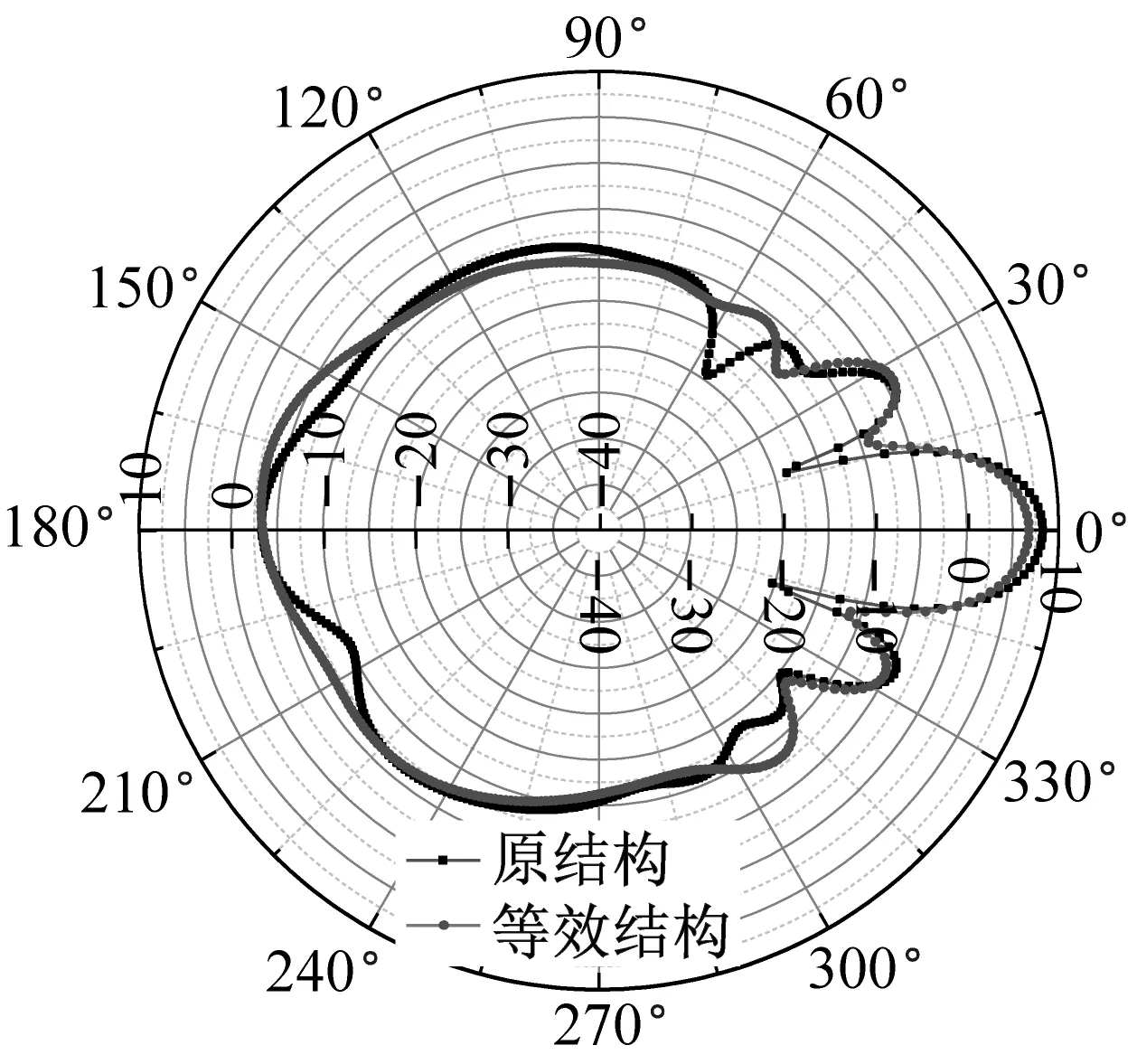
(g) 3 000 Hz

(h) 4 000 Hz

(i) 5 000 Hz图14 目标强度指向性对比Fig.14 Comparison of target target strength directivity

4 结 论

本文利用参数反演方法，对内部含耐压圆柱体的非水密结构的声目标强度进行了预报。一方面，在已有的遗传算法反演声学参数的基础上加入了非线性规划，在算法中充分考虑了斜入射、多次散射、吻合效应以及横波波速阈值的影响，并以此建立了双层弹性介质层反演模型，该反演模型与原结构在各个角度下均具有基本相同的反射系数与透射系数。另一方面，本文建立了两种内部含耐压圆柱体的非水密结构用以对比原结构与等效结构的目标强度，从整个频段目标强度对比结果来看，收发合置情况下，原结构与等效结构的各个频率下的目标强度值基本一致，各个方向入射时的研究频段整体误差在1.5 dB以下；30°收发分置情况下，原结构与等效结构的各个频率下的目标强度值波峰波谷的趋势相同，各个方向入射时的研究频段整体误差在2 dB以下。从各个频率下的目标强度指向性来看，中高频段，原结构与等效结构目标强度吻合程度较好；中低频段，原结构与等效结构目标强度指向性基本一致，但幅值存在差异；总体来看，-30°～30°范围内，除个别频率外，原结构与等效结构目标强度基本吻合。

综上所述，本文所构建的参数反演方法在解决外壳敷设声学覆盖层，内部存在结构物的非水密结构声目标强度预报方面具有一定优势。