单回路液氦脉动热管气液两相流数值模拟
吕秉坤 徐 冬 王 维 施雅然 信纪军 方志春 李来风
(1 松山湖材料实验室 东莞 523808)
(2 中国科学院低温工程学重点实验室(理化技术研究所)北京 100190)
1 引言
脉动热管(Pulsating Heat Pipe,PHP)是20 世纪90 年代出现的一种新型热管,由日本的Akachi 最早提出。它是将一根内径较小(一般为0.5—3 mm)的毛细管在蒸发段和冷凝段之间反复弯折并将首尾连接形成的蛇形结构,其余部分为绝热段。其工作原理是将管内抽成真空后充入工作介质,由于管径足够小,在表面张力的作用下,接近饱和态的两相流体工质在毛细管内以气塞和液塞的形式随机交替分布。当管的一端(蒸发段)被加热时,工质吸热导致气泡生长和蒸气压力的增大;与此同时,气泡在另一端(冷凝段)凝结,气泡会收缩破裂,压力下降。气泡的生长和破裂导致蒸发段和冷凝段存在压差以及相邻管子之间存在压力不平衡,从而推动工质在管内脉动运动或单向循环流动,通过气液相变的潜热和液塞流动时的显热传递热量。
脉动热管由于其结构紧凑、性能良好、可靠、灵活、无噪声且耐用,经过优化还可实现无重力运行,已经成为最具创新性、有效性的两相换热系统之一,在微电子领域和工业领域得到了广泛应用,例如太阳能利用、电子设备冷却、空间热管理和余热回收等。在低温领域,脉动热管在超导磁体高效冷却应用中也有很大的潜力。
虽然脉动热管的结构非常简单,但由于脉动热管传热传质过程中流体力学和热力学的耦合作用,使得脉动热管的运行机制非常复杂。对于低温脉动热管,循环流动是其高效传热的基础。然而低温脉动热管的理论研究处于起步阶段,低温脉动热管的可视化到目前为止还没有被实现,因此通常采用数学建模和数值模拟两种方式来研究低温脉动热管的运行机理。但是,一维的数学模型由于过多的简化与假设,模拟结果与实际的两相流流动仍有很大的差别。随着计算机计算能力的发展,利用计算机进行二维或三维的数值模拟成为主要的研究手段。印度萨尔达尔瓦拉布巴伊国家技术学院的Sagar 等人[1]采用多相流VOF(Volume of Fluid,VOF)模型对近临界直径二维低温脉动热管进行了数值模拟,发现与地面条件相比,在低重力条件下,低温脉动热管的换热性能得到了改善。随后,他们对另一个蒸发段、冷凝段温度均设为恒定的二维低温脉动热管进行了数值模拟[2],研究了不同运行条件下液氮的体积分数结果,对工质温度、绝热壁面温度和流动循环速度进行了分析。上海理工大学的唐恺等人[3-5]利用Fluent 软件中的多相流VOF 模型,分别研究了氮和氦工质低温脉动热管的流型和充液率、加热功率、内径和倾斜角等参数对性能的影响。哈尔滨理工大学的徐金柱等[6]对单环路液氢温区脉动热管进行了CFD(Computational Fluid Dynamics)数值模拟,模拟的传热热阻与实验值的误差不超过15%。
上述模拟研究中,由于模型的简化与假设,模拟结果与脉动热管内部的两相流仍存在一定程度上的差异,且液氦脉动热管的模拟数据十分有限。为了准确描述液氦脉动热管的气液两相流,本研究建立了单回路液氦脉动热管CFD 模型,并对其初始状态和运行状态的流体流动与传热进行了分析。
2 液氦脉动热管模型建立
2.1 几何模型
本研究应用ANSYS 2020R2 建立液氦脉动热管的模型并求解。采用建模软件ANSYS DesignModeler软件绘制二维单回路液氦脉动热管的几何模型,如图1所示。液氦脉动热管模型的冷凝段、绝热段和蒸发段长度分别为5 mm、5 mm、5 mm,弯头直径为3 mm,弯头部分也视为绝热段,内径为0.5 mm,采用竖直放置底部加热的方式。

图1 二维单回路液氦脉动热管几何模型和网格划分Fig.1 Geometric model and mesh generation of two-dimensional single loop helium pulsating heat pipe
采用ANSYS Meshing 软件对该脉动热管模型进行结构化网格划分。太少的网格计算时间虽然短,但气液界面不够清晰,影响模拟结果,太多的网格必然耗费更多时间计算。在完成网格独立性检验后,确定节点数为32 844,网格数为31 280。
2.2 控制方程
低温脉动热管内部的流动为气液两相流动。应用VOF 方法来跟踪脉动热管每个单元中基于气相和液相体积分数αv和αl的表面界面,其中下标v 和l 分别代表气相和液相。在控制体积中
在这个模型中,气相被认为是可压缩的理想气体,液相不可压缩,给出了两相体积分数的连续性方程
式中:ρv和ρl和分别为蒸气和液体的密度,kg/m3;为速度矢量,m/s;Sl和Sv分别为液相和气相的源项,kg/(m3·s);和分别为从蒸气到液体的质量转移以及从液体到蒸气的质量转移,kg/(m3·s)。
其中蒸发冷凝过程可以用Lee 模型表示。如果Tl>Tsat,发生蒸发过程
如果Tv 式中:Tl和Tv分别为液体和蒸气的温度,K;Tsat为饱和温度,K;rlv和rvl为传质时间的松弛因子,这些系数影响数值收敛的精度和界面温度。根据Lee 等人[7]的研究结果,通常设置为默认值0.1,使界面温度在数值上保持接近工质的饱和温度。 动量方程在式(6)中求解,它依赖于所有相的体积分数。 式中:ρ为控制体积内的平均密度,kg/m3;为速度矢量,m/s;p为压力,Pa;μ为黏度,Pa·s;为重力加速度,m/s2;为由弯曲界面引起的拉普拉斯方程计算的体积力,N/m3。 表面张力是由于流体中分子间的内聚力而产生的,它产生的表面力在小通道中占主导地位。对于表面张力的建模,采用ANSYS Fluent 中的连续表面力(Continuum Surface Force,CSF)模型[8]。在VOF 模型中,将表面张力作为动量方程的源项加入到动量方程中,如式(7)所示: 本模型的能量方程为: 式中:E为热力学能,J/kg;λeff为有效导热系数,W/(m·K);Sh为相变引起的能量源项,W/m3,它是由传质速率乘以潜热Sh=-hLHlv=hLHvl得到的。 本研究应用ANSYS Fluent 对建立的模型进行求解。氦气的物性随温度的变化而变化,为了使模拟更接近真实情况,采用美国国家标准技术研究所(NIST)开发的Refprop 软件获得不同温度下氦气的物性并拟合成多项式的形式,其中密度、定压比热、热导率、运动黏度系数的多项式拟合公式分别如式(9)、(10)、(11)、(12)所示。 液氦被视为不可压缩流体,因此其物性随温度变化可以忽略不计,选用4.215 K 温度下的物性参数进行计算。 两相流模型VOF 方程采用显式形式,无量纲库朗数设置为0.25,选用隐式体积力方程。为使模型更快收敛,饱和温度设置为4.215 K。其它关于模型的求解设置列于表1 中。 表1 二维液氦脉动热管数值模拟Fluent 求解设置Table 1 Solution setting of two-dimensional helium pulsating heat pipe by Fluent numerical simulation 为了模拟液氦脉动热管的初始状态,将初始状态每个网格的温度设置为4.215 K,充液率为50%。边界条件设置为恒温4.215 K。采用ANSYS Fluent 求解计算,计算稳定后得到脉动热管的初始气液分布状态,如图2 所示。图2a 展示了二维单回路液氦脉动热管初始状态的气液分布云图。可以看出在表面张力和重力的共同作用下,管内工质形成气塞和液塞交替分布的静止状态,气塞和液塞的大小和长度是随机的,且气液分界面明显。初始状态下液氦脉动热管内的温度均保持在4.215 K 左右,蒸发段和冷凝段没有温差,如图2b 所示。同时,如图2c 所示,初始状态下液氦脉动热管处于饱和状态,不存在质量传递。当工质充注到液氦脉动热管后,由于毛细作用,管内的工质会形成随机分布的气塞与液塞,初始状态的气液分布为液氦脉动热管的启动提供了基础。 图2 二维单回路液氦脉动热管初始状态云图Fig 2 Initial state contour diagram of two-dimensional single loop nitrogen pulsating heat pipe 改变边界条件为蒸发段和冷凝段施加恒热通量边界,加热和冷却功率均为0.4 W,绝热段设定为绝热边界条件,二维单回路液氦脉动热管进入运行状态。图3 展示了二维单回路液氦脉动热管运行状态的气液分布云图。从图中可以看出,当蒸发段和冷凝段的边界改变后,液氦脉动热管管内工质不再保持静止状态。在加入热负荷的前0.4 s 内,由于蒸发段壁面被加热,液膜吸收热量并蒸发,气塞不断产生并膨胀,同时冷凝段内气体温度低于饱和温度被冷凝为液体,气塞收缩并破碎,因此蒸发段和冷凝段之间形成压差,压差驱动力推动两根通道内的气塞会由于膨胀作用同时向冷凝段流动。此外,在50%充液率下,管内工质的流型为塞状流。在0.4 s 至1.4 s 时间段内,随着蒸发段液膜的不断蒸发,气塞逐渐变长,脉动热管内的压力差也不断增加。此时左侧通道内的压力低于右侧通道内的压力,因此左侧管道内的工质改变流动方向向下流动,右侧工质继续向上流动。这是由于蒸发段气化核心产生的位置具有一定的随机性,蒸发段内气塞的位置和大小因此会产生差异。当压差足够克服重力以及毛细力时,管内工质向同一方向运动。此阶段流动方式为单方向循环流动。在1.4 s至1.6 s 内,由于蒸发段的持续加热,蒸发段内温度持续升高,核态沸腾发生,蒸发段液膜吸热蒸发更加剧烈,这时左侧通道由于强烈的气液相变,产生了更大的推动力,工质改变流动方向,左侧通道为上升管,右侧通道为下降管,工质流动方式为逆向流动。因此,在运行阶段,该单回路液氦脉动热管管内工质经历了以下3 种流动状态:两侧通道内同时向冷凝段运动、单方向循环流动、逆向循环流动。 图3 二维单回路液氦脉动热管运行状态气液分布云图Fig.3 Gas-liquid distribution contour diagram of working state of two-dimensional single loop helium pulsating heat pipe 图4 展示了二维单回路液氦脉动热管的温度分布云图。该模拟工况下,随着蒸发段和冷凝段壁面以恒定功率传热,脉动热管内蒸发段的温度逐渐升高,反之,冷凝段的温度逐渐降低,蒸发段的温度在1.2 s时升至最高5.6 K,冷凝段的温度则降至3.4 K。在0.6 s 至1.2 s 期间,由于工质携带热负荷往逆时针方向运动,右侧通道为上升管,左侧通道为下降管,因此,右侧通道内蒸发段的热流也随着工质流动方向朝冷凝段运动。同时,左侧通道内的热流朝蒸发段运动。在1.2 s 以后,由于脉动热管管内工质的运动方向改变为顺时针循环流动,右侧通道内热流转变为向蒸发段运动,左侧通道内的热流转变为向冷凝段运动。由此可见,单回路液氦脉动热管运行过程中蒸发段温度升高,冷凝段温度降低,其传热方向与工质流动方向相同。 图4 二维单回路液氦脉动热管运行状态温度分布云图Fig.4 Temperature contour diagram of working state of two-dimensional single loop helium pulsating heat pipe 图5 展示了二维单回路液氦脉动热管运行状态的质量传递云图。从图中可以看到,单回路液氦脉动热管运行时相变和质量传递主要在蒸发段和冷凝段发生。由于蒸发段有热量输入,通道内的液氦温度超过饱和温度,产生核态沸腾,液膜蒸发,产生气泡,且处于蒸发段的气塞也会随着液膜蒸发而膨胀。反之,冷凝段内有热量输出,工质温度低于饱和温度,处于过冷状态,氦气冷凝为液相,气塞逐渐收缩。蒸发段和冷凝段由于相变传质而具有压力梯度,驱动管内的工质在蒸发段和冷凝段之间运动,从而实现热量的传递。由此可知,液氦脉动热管运行过程中由于冷热端的温度差产生的相变是造成压力差和工质流动的原因,而工质流动实现了热量的传递。由模拟结果可知,液氦脉动热管自身具有自激振荡的特性,因此不需要增加额外的驱动功率就能传递热负荷。 图5 二维单回路液氦脉动热管运行状态质量传递云图Fig.5 Mass transfer contour diagram of working state of two-dimensional single loop helium pulsating heat pipe 为了探究液氦脉动热管的运行机理,使用ANSYS Fluent 中的多相流VOF 模型、表面张力模型(CSF 模型)以及传热传质模型(Lee 模型),模拟了二维单回路液氦脉动热管的初始状态气液分布以及运行状态的流动与传热。其中初始状态的气液交替分布为液氦脉动热管的启动提供了基础。该单回路液氦脉动热管运行时管内工质经历了3 种流动状态:两侧通道内同时向冷凝段运动、单方向循环流动、逆向循环流动。在50% 充液率下,该脉动热管的流型为塞状流。通过数值模拟发现,在薄膜蒸发/冷凝和气泡压缩/膨胀的共同作用下,蒸发段内的气塞温度大于相同压力下的饱和温度,处于过热状态;冷凝段内的液塞温度小于相同压力下的饱和温度,处于过冷状态。由模拟结果可知,液氦脉动热管依靠内部的工质流动及蒸发冷凝来实现热量的传递,运行的动力来源于管内的压力差。模拟结果对理解液氦脉动热管的运行和传热机制有很大帮助。2.3 数值模拟方法

3 数值模拟结果及分析
3.1 液氦脉动热管初始状态
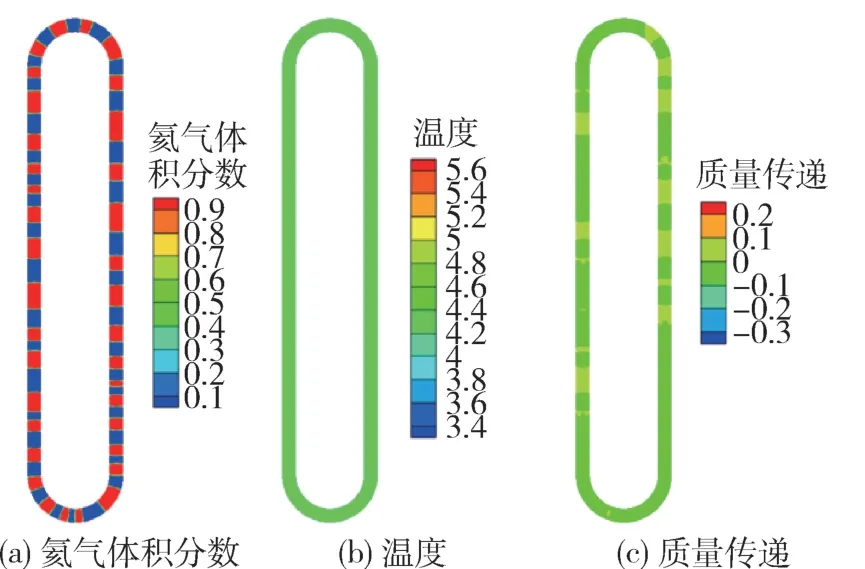
3.2 液氦脉动热管运行状态的流动分析

3.3 液氦脉动热管运行状态的传热特性


4 结论

