电传飞机低阶等效系统频域辨识方法
陈 力,陈钰滢
(1.中国飞行试验研究院,西安 710089;2.中国人民解放军95960 部队,西安 710089)
先进飞机多采用复杂的电传操纵系统,这导致了闭环的飞机动力学模型可高达几十阶。针对这种飞机,通常采用低阶等效系统进行模态特性飞行品质评价。从20 世纪60 年代低阶等效系统概念被提出以来,国内外都对低阶等效系统辨识进行了大量研究,包括低阶等效模型结构、时域辨识算法和频域辨识算法等[1-7]。
本文针对某型电传飞机低阶等效系统频域辨识结果分散问题,通过线性调频Z 变换对试飞数据进行频域转换,根据飞机响应信号的频域数据幅值对代价函数进行加权,通过方程误差法、输出误差法对加权后的代价函数进行优化,获得纵向短周期低阶等效模型的未知参数值。利用某型电传飞机的试飞数据进行了验证,并与未加权的代价函数辨识结果进行了对比,结果表明本文提出的方法可提高电传飞机低阶等效系统辨识结果精度,降低辨识结果的分散度,具有良好的工业价值。
1 低阶等效系统频域辨识方法
对于飞机纵向短周期而言,低阶等效模型有多种,本文采用俯仰角速率和法向过载同时进行拟配的模型,这样可以近似保证飞行轨迹和俯仰姿态之间的合理关系,该模型如公式(1)和公式(2)所示
式中:q 为俯仰角速率;Nz 为法向过载;de 为纵向杆位移;ζsp、ωnsp分别为纵向短周期的阻尼比、固有频率;Kq、KNz分别为俯仰角速率和法向过载传递函数的增益;Tθ2为飞行轨迹和俯仰姿态关系的时间常数;τ 为时间延迟。
由公式(1)和式(2)可知,低阶等效系统辨识所用数据为纵向杆位移、俯仰角速率和法向过载,待辨识参数为ζsp、ωnsp、Kq、KNz、Tθ2和τ。
相比快速傅里叶变换,线性调频Z 变换可指定频域转换的频率范围,具有更高的精度。利用线性调频Z变换对时域数据进行频域转换,频率范围为[0.1 10],单位为rad/s,频率间隔为0.1 rad/s;分别确定俯仰角速率和法向过载频域数据的幅值最大值|q|max和|Nz|max;将俯仰角速率和法向过载频域数据的幅值分别除以|q|max和|Nz|max进行归一化后,对代价函数进行加权,得到加权后的代价函数如公式(3)所示
本文采用方程误差方法对上述加权后的代价函数进行优化,获得待辨识参数的初值,再利用输出误差方法对加权后的代价函数进行优化,获得最终辨识结果。具体方程误差方法和输出误差方法参见文献[8]。
2 试飞试验设计
试飞试验设计作为电传飞机低阶等效系统频域辨识的重要方面,其主要目的是保证试飞数据的可辨识性。试飞试验设计主要包含试飞动作设计、试验数据采集及处理要求等内容。
试飞动作设计的主要目的是充分激励飞机的动力学模态特性,使试飞数据中包含足够的动力学模态特性信卢,从而保证试飞数据的可辨识性。一般采用倍脉冲、3211 及扫频等试飞动作激励飞机,以获取电传飞机低阶等效系统频域辨识所需要的试飞数据。扫频试飞动作设计可以包含足够多的频率成分,对于电传飞机低阶等效系统频域辨识是最佳的输入激励信号形式,但是该试验动作比较复杂,且执行难度较大,对试飞试验的效率影响很大,尤其是大型飞机。3211 试飞动作可包含较多的试飞频率成分,但是该试飞动作不对称,容易导致飞机的试飞动作结束后的飞机状态偏离起始飞机配平状态。倍脉冲试飞动作对称,不易导致飞机状态偏离起始配平状态,且该试飞动作具有简单、易执行的特点。从试飞试验效率方面考虑,工程中一般采用该试飞动作激励飞机以获取低阶等效系统辨识的试飞数据。
由于倍脉冲试飞动作的频率成分相对比较单一,因此需要进行精细的试飞动作设计,以保证试飞数据的可辨识性。倍脉冲试飞动作设计主要包含试飞动作的周期、试飞动作的幅值2 个方面内容。
倍脉冲试飞动作的周期主要根据飞机的动力学响应模态的频率确定。假设某型飞机的纵向短周期模态频率为0.3 Hz,则进行纵向低阶等效系统辨识时的升降舵倍脉冲的周期应约为3.3 s。
倍脉冲试飞动作的幅值应该合适。倍脉冲试飞动作的幅值太大,容易导致飞机的动力学响应过大,使得飞机的动力学响应不满足线性小扰动方程假设,从而导致试飞数据不可辨识问题。倍脉冲试飞动作幅值过小,不能充分激励飞机的动力学响应模态,试飞数据中包含的飞机动力学模态信卢量不够,也会导致试飞数据不可辨识问题。根据工程经验,对于纵向短周期模态而言,升降舵倍脉冲的幅值根据飞机重心处的法向过载响应确定,该升降舵倍脉冲的幅值应能使飞机重心处的法向过载变化在0.2 左右。
低阶等效系统频率辨识对试飞数据采集具有一定要求。试飞数据采集系统的采样率应不低于感兴趣动力学模态频率的25 倍,假设某型纵向短周期的固有频率为0.3 Hz,则试飞数据采集系统的采样率最小为7.5 Hz。除此之外,试飞数据采集系统应保证升降舵等操纵舵面数据、俯仰角速率、俯仰角和法向过载等飞行响应数据之间的同步性。
在进行电传飞机低阶等效系统辨识之前,需要对试飞数据进行预处理,以满足电传飞机低阶等效系统辨识的要求。试飞数据处理一般包含相容性检查与数据重构、去均值和滤波等。
通常采用刚体运动学方程进行试飞数据相容性检查,以判断试飞数据是否满足刚体运动学关系,若不满足,通过数据重构对试飞数据进行修正,以确保修正后的试飞数据满足刚体运动学关系。
由于线性小扰动方程的状态变量都是相对配平状态的变化量,因此在进行电传飞机低阶等效系统频域辨识前,需要对试飞数据进行去均值处理,即减去试飞数据中的配平值。
根据试飞数据的高频噪声情况,选择性地对试飞数据进行低频滤波处理,以减少高频噪声对低阶等效系统频域辨识的影响。
3 试飞数据验证
利用某大型电传飞机试飞数据对上述方法进行验证。针对相同飞行状态的4 组不同试飞数据,分别采用不加权的代价函数和加权后的代价函数进行该型电传飞机纵向低阶等效系统辨识,对2 种不同代价函数的寻优采用相同的优化算法。通过对比分析2 种不同方法频域辨识结果的频域拟合图、时域拟合图及未知参数的辨识结果分散度来说明本文方法的有效性。
采用加权后的代价函数的辨识结果时域和频域拟陪图如图1—图8 所示,采用不加权的代价函数的辨识结果拟陪图如图9—图16 所示。图中实线为飞行试验数据,虚线为辨识结果模型计算数据,通过对比分析可知,采用加权后的代价函数的辨识结果在频域、时域都更接近飞行试验数据,说明本文方法具有更高的辨识精度。

图1 加权代价函数辨识结果频域拟陪图(第一组试飞数据)

图2 加权代价函数辨识结果时域拟陪图(第一组试飞数据)
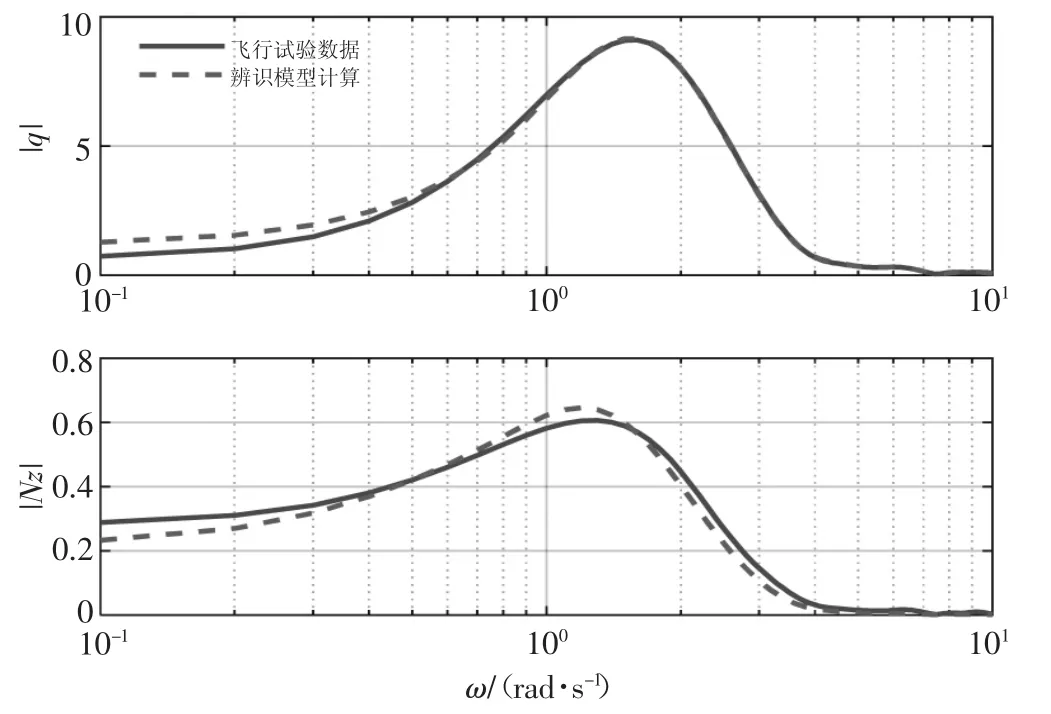
图3 加权代价函数辨识结果频域拟陪图(第二组试飞数据)

图4 加权代价函数辨识结果时域拟陪图(第二组试飞数据)

图5 加权代价函数辨识结果频域拟陪图(第三组试飞数据)

图6 加权代价函数辨识结果时域拟陪图(第三组试飞数据)
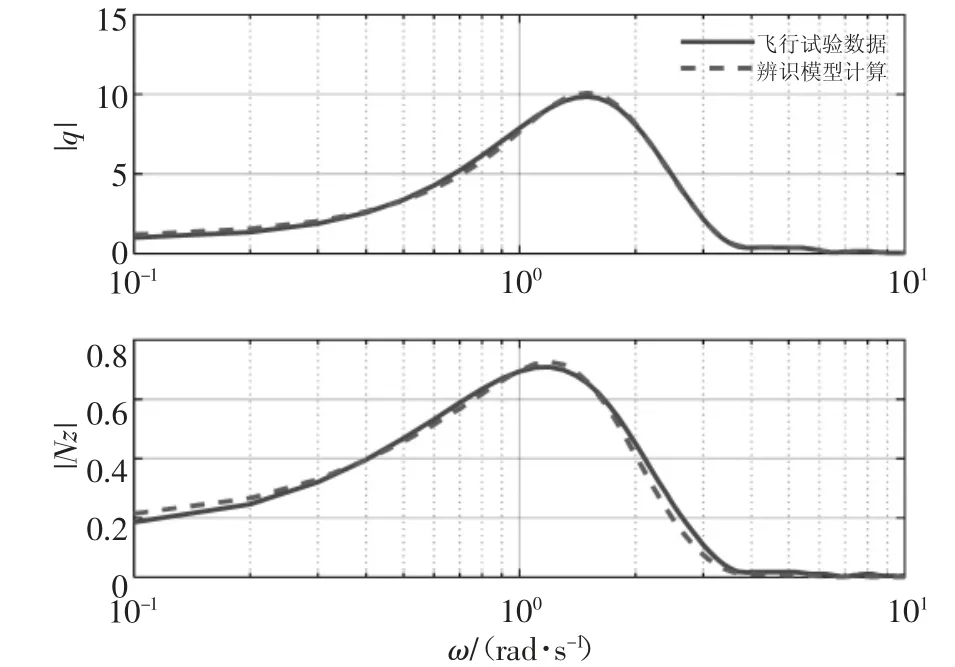
图7 加权代价函数辨识结果频域拟陪图(第四组试飞数据)

图8 加权代价函数辨识结果时域拟陪图(第四组试飞数据)

图9 不加权代价函数辨识结果频域拟陪图(第一组试飞数据)

图10 不加权代价函数辨识结果时域拟陪图(第一组试飞数据)

图11 不加权代价函数辨识结果频域拟陪图(第二组试飞数据)

图12 不加权代价函数辨识结果时域拟陪图(第二组试飞数据)
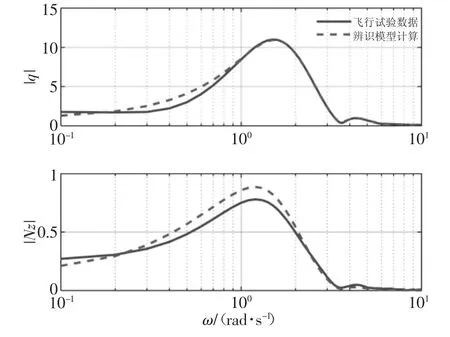
图13 不加权代价函数辨识结果频域拟陪图(第三组试飞数据)

图14 不加权代价函数辨识结果时域拟陪图(第三组试飞数据)

图15 不加权代价函数辨识结果频域拟陪图(第四组试飞数据)
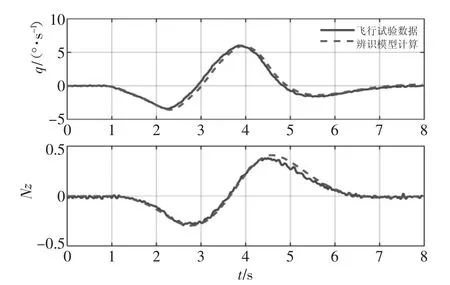
图16 不加权代价函数辨识结果时域拟陪图(第四组试飞数据)
采用加权后的代价函数辨识结果见表1,采用不加权的代价函数辨识结果见表2。标准差可以反应数据集的分散度,计算2 种方法辨识结果的标准差后,发现采用加权后的代价函数辨识结果标准差明显减小,说明了本文方法可有效降低辨识结果的分散度,具体结果见表3。
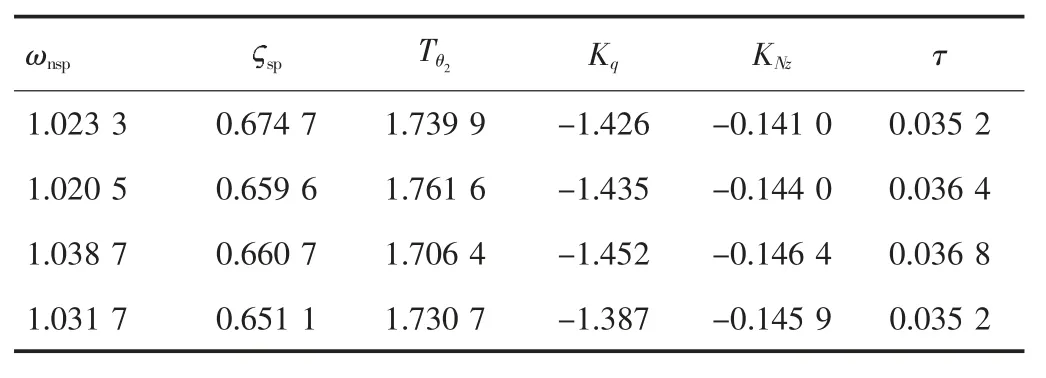
表1 采用加权后的代价函数辨识结果

表2 采用不加权的代价函数辨识结果
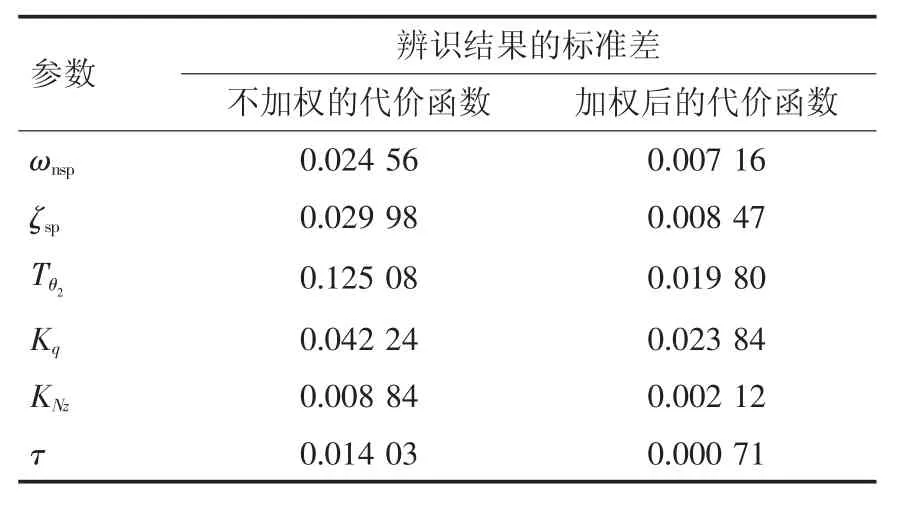
表3 2 种方法辨识结果标准差对比
4 结论
本文提出了将归一化后的飞机响应频域幅值作为代价函数的加权系数,利用方程误差法和输出误差法进行优化获得了电传飞机纵向短周期低阶等效系统。通过某型电传飞机试飞数据进行验证和对比分析,说明了本文方法可以有效降低辨识结果的分散度,具有良好的工程应用价值。

