基于时间序列复杂网络的癫痫脑电分类研究*

杨晓利 杨 彬 李振伟 吴晓琴

（河南科技大学医学技术与工程学院 洛阳 471000）

1 引言

癫痫是一种常见的神经系统疾病，根据统计显示，全世界约有6000 万名癫痫患者［1］，我国约有900 万患者，并且每年约增加40 万～60 万的患者。癫痫疾病严重危害着人类的健康，其中药物难治性癫痫约占癫痫患者总人数的30%～35%［2］，癫痫的反复发作会给患者带来认知功能障碍，严重影响着患者的生活质量。因此，加强对癫痫疾病的研究对癫痫疾病的诊断治疗以及改善患者的生活质量具有重要意义。癫痫发作时会在大脑区域突然出现异常的放电活动，出现棘波、尖波等波形的脑电信号，脑电图就成为诊断和治疗癫痫病的主要手段。而脑电图的分析是一项耗时耗力的工作，临床诊断时，需要由医生完成，效率低下，存在主观性，而且医生在长时间的工作下，有很大可能出现误判的问题，因此，需要对癫痫进行自动、快速识别。

目前已经提出了多种方法来自动检测癫痫，对癫痫进行分类，主要由特征提取和特征分类组成。特征提取主要有线性特征和非线性特征，线性特征包括时域［3～4］、频域［5］和时频域［6～7］的方法，非线性特征包括各种熵［8］和指数［9］。特征分类主要是模式识别问题，近年来，机器学习技术迅速发展，SVM［10］，神经网络［11］等算法被应用于癫痫脑电的识别。Hussain L［12］基于癫痫脑电信号从时域到频域、统计、复杂度和小波的熵测度，提出了多域特征，采用了机器学习分类器。韦晓燕等［13］提出基于深度学习的卷积神经网络模型来识别不同阶段的癫痫EEG数据，设置多层深度卷积神经网络对数据进行学习，完成不同癫痫EEG 分期的分类，该方法在临床数据中的测试准确率均超过了90%。MeiseL C等［14］采用深度学习的方法对皮层脑电、心电关于癫痫状态的信息进行了对比分析，发现深度学习方法通常胜过更传统的机器学习方法，这突出了深度学习从数据中提取信息内容的总体优越能力。近年来，复杂网络理论在各个领域快速发展，脑信号的研究转换成脑网络的研究成为了近年来的研究热点，尤其是时间序列复杂网络的分析研究，并且广泛应用到各类脑疾病研究中［15～18］。利用复杂网络方法，从网络的角度来研究人脑功能，为脑部疾病研究提供了新的方向。本文将复杂网络理论应用到癫痫分类研究，从癫痫脑电信号的时间序列构造出癫痫脑电复杂网络，计算相关特征参数应用于分类器进行分类。

2 方法

2.1 网络构造

Lacasa L［19］提出的可见性算法可将任意时间序列构造成复杂网络，即时间序列的每个采样点作为复杂网络的节点，节点之间的连接作为复杂网络的连接边，Luque B［20］在此基础上提出了水平可见性算法，即当任意两个节点之间的采样值小于这两个节点之间的最小值时，这两个节点即有连接，反之没有连接。可见性算法与水平可见性算法都是将采样点作为复杂网络的节点，如果采样频率高且记录时间长，那么网络的节点会相当巨大，网络就会相当复杂，会产生巨大的计算量，造成计算困难。因此，本文将时间序列进行分段处理，每一段视为复杂网络的节点，在不丢失时间序列信息的前提下，从每一段时间序列的全局考虑，而不是单个采样点，对每段时间序列的Pearson 相关性进行成对计算（每段信号同时进行自相关），得到大小为N×N的Pearson 相关系数矩阵，此矩阵作为网络的连接边。

假设两段时间序列为X=[X1，X2，…，Xn] ，Y=[Y1，Y2，…，Yn]，则X与Y的Pearson相关为

由构造出的网络进行网络特性分析，分析网络的平均最短路径长度、全局效率、局部效率、节点度平均度和聚类系数［21］来构造分类器的特征向量，以此实现癫痫脑电的分类。

2.2 分类器融合

本文使用SVM，逻辑回归（Logistic Regression，LR）和K-NN 多种分类器对癫痫脑电信号分类识别，对多种算法进行对比分析。并且在考虑到使用单个分类器可能存在准确率不高的问题，为了提高准确率，采用一种分类器融合的方法，将分类器之间的优势进行互补。本文将SVM，LR 和K-NN 三种分类器的预测结果进行融合处理，融合方法采用投票原理，即少数服从多数，投票多数的结果即为融合分类器的分类结果。假设样本为x，N(i，x)是x的第i个分类器的分类结果，定义Ti(x，yj)为第i个分类器对x分类为yj的得分：

将所有分类器对x的分类结果进行统计分析，得分半数以上的分类结果就对作为融合分类器的分类结果。融合分类器对x的投票规则如下：

其中a为松弛度，本文中取a=0.5，也就是说，单分类器的分类结果有一半以上则被认为是融合分类器的分类结果。

3 实验

3.1 数据处理

本文用于研究的数据来自于德国波恩大学脑电图数据库，该数据集包括A、B、C、D、E五组，五组中都是记录的单通道脑电信号，每组含有100 个样本。采样频率为173.61Hz，时长23.6s，A 组和B 组记录的是五名健康受试的脑电图，C、D 两组记录于癫痫患者的发作间期，E 组记录的是癫痫患者发作期的脑电信号。为便于进一步的研究，将分类问题列为三类，第一类：A-E，第二类：AB-CDE，第三类：ABCD-E。

首先对信号进行预处理，脑电信号记录长度为23.6s，在考虑到信号记录时可能存在干扰，去掉前1s 和后0.6s，保留22s 时长的信号，首先采用3 层小波变换对信号进行滤波处理，然后分别以1s和0.5s长度对信号进行分段。第一组以1s 长度对22s 信号进行分段，每一段作为节点，得到22 个节点；第二组以0.5s 长度对信号进行分段，每一段作为节点，得到44 个节点。然后对分段后的信号分别两两进行Pearson 相关，由此得到构造复杂网络连接边的矩阵，第一组矩阵大小为22×22，第二组矩阵大小为44×44。通过设置阈值P，对矩阵二值化处理，矩阵中的值大于P置1，小于等于P置0，得到二值化矩阵（对角线为每段信号自相关，置0 处理）。P为0.3 时，节点的连接矩阵如图1，并对网络可视化如图2。

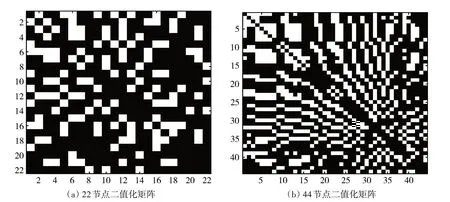
图1 网络的连接矩阵

图2 网络可视化图

3.2 特征提取

通过对数据处理得到复杂网络的连接矩阵，根据连接矩阵计算网络的特征参数，平均最短路径长度、全局效率、局部效率、节点度平均度和聚类系数，并对特征参数进行统计分析。阈值P为0.3时，对特征值进行统计分析，22 节点网络特征值盒形图如图3，44节点网络特征值盒形图如图4。

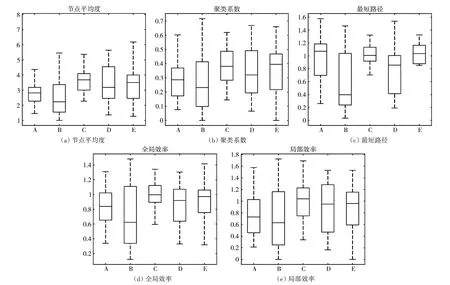
图3 22节点网络特征参数盒形图

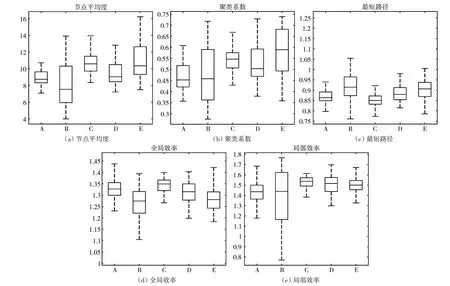
图4 44节点网络特征参数盒形图

由统计分析结果可知，数据集A-E之间的五个特征参数存在统计学差异，数据集AB-CDE之间的五个特征参数存在统计学差异，因此在对数据集A-E和数据集AB-CDE分类时，将平均最短路径长度、全局效率、局部效率、节点度平均度和聚类系数作为5维特征向量；而数据集C-D-E之间的特征参数无明显统计学差异，但是节点数量增加，特征参数的统计学差异有所增大，

但是局部效率仍无明显特征差异，因此在对数据集ABCD-E分类时，将最短路径长度、全局效率、节点度平均度和聚类系数作为4维特征向量。

3.3 实验结果与分析

根据特征向量使用SVM，LR 和K-NN 进行分类，采用5 折交叉验证［22］的方式计算准确率。并使用融合分类器SVM+LR+K-NN 计算准确率。当阈值P为0.3时，分类结果如下。

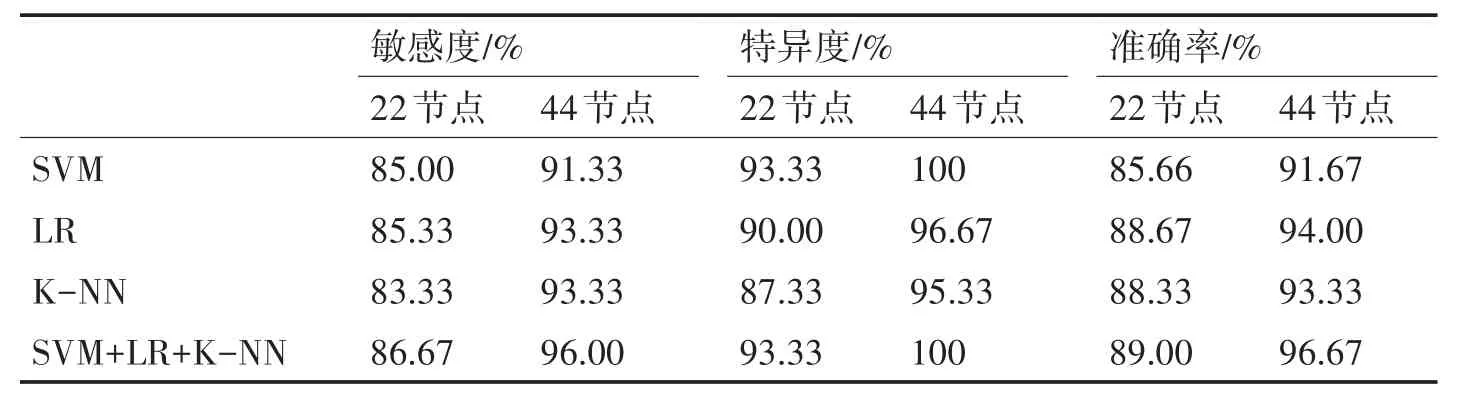
表1 A-E分类结果

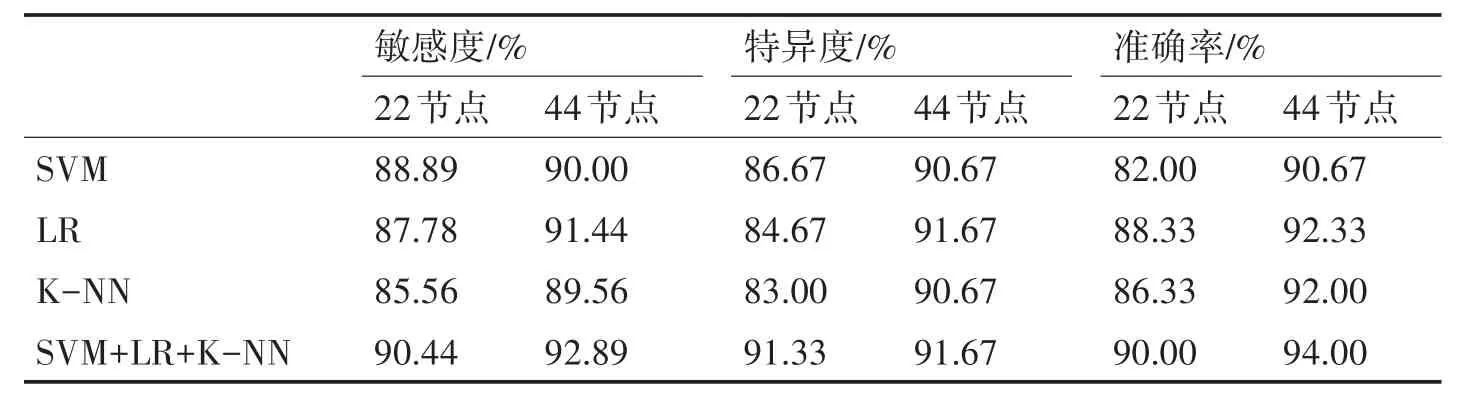
表2 AB-CDE分类结果

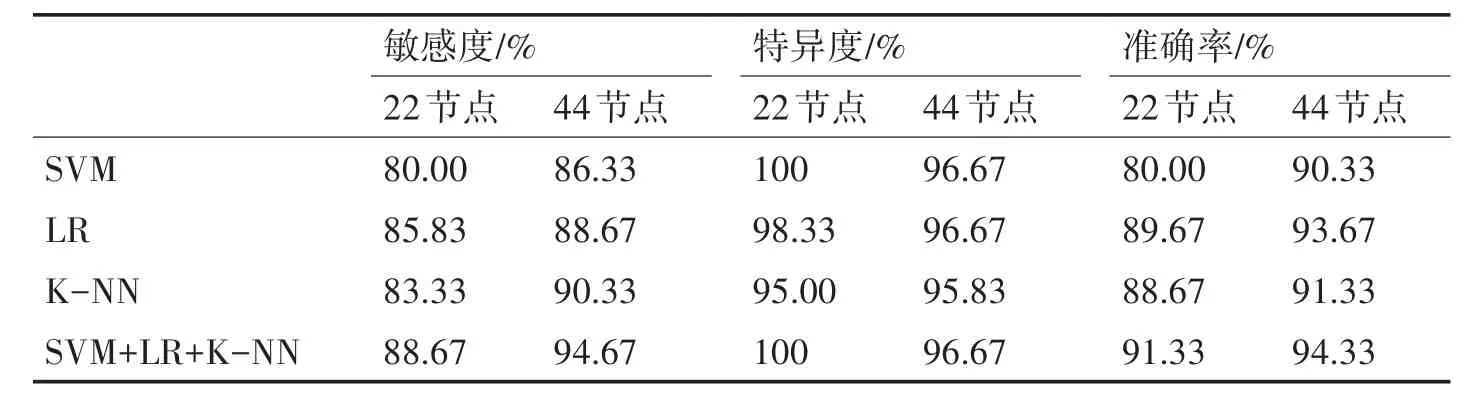
表3 ABCD-E分类结果

由分类结果可知，在对三类数据集分类时，对44 节点网络的分类准确率均高于22 节点网络，由此可知，网络节点数量增多，更能包含信号的特征信息。并且在单分类器上，LR 分类器在三类数据集分类效果表现最佳，K-NN 分类器次之。而使用融合分类器，在三类数据集分类上准确率均有提高，在对数据集A-E 分类时，准确率达到了96.67%，对数据集AB-CDE 分类时，准确率达到94.00%，对数据集ABCD-E 分类时，准确率达到了94.33%，有效的识别出了癫痫脑电信号。在构造网络时，初始阈值P 设置为0.3，没有考虑阈值对网络的影响，因此，为了验证阈值对网络的影响，在三个分类问题的数据集上，对44 节点网络的阈值从0.2以0.01增加到0.3，并进行分类分析。阈值过大，连接边就会减少，从而造成网络信息的丢失，而且阈值太小，连接边就会过多，造成网络信息的冗余，因此选择从0.2 增加到0.3。在3 个分类集上，阈值增加的分类准确率如图5。

图5 三个分类集不同阈值对比分析

由结果可知，随着阈值的增大，在三类数据集上的分类准确率总体成上升趋势，证明了本文阈值选取的合理性。并且在三类数据集的分类问题上，SVM 表现最为平稳，LR分类器虽然总体表现最佳，但是存在一定波动，而采用融合分类器更好地融合了各分类器的优点，实现了更高的分类准确率。

4 结语

本文提出一种从时间序列构造复杂网络的癫痫脑电分类方法，提取癫痫脑电复杂网络的统计特征量，采用SVM，LR 和K-NN 进行分类，LR 分类器表现效果相对出色，而融合分类器的分类效果更佳。在本文的研究中，对数据集A-E准确率达到了96.67%，对数据集AB-CDE 准确率达到94.00%，对数据集ABCD-E，准确率达到94.33%，实现了对癫痫脑电高质量的分类，虽然本文方法能够有效地识别癫痫脑电信号，但是还有更进一步的研究空间，增加节点数量，以及更进一步考虑阈值的选取。实验结果表明，本文提出的方法可用于癫痫的检测，对癫痫的自动检测有重要的意义，为癫痫检测研究提供了新的思路，并且对了解脑的病理症状及临床诊断具有重要意义。