星载辐射计动平衡概述及在轨动平衡技术研究

叶志彪，高一丹，黄佳雷，金旭鑫，何嘉恺，翁艺航

（上海航天电子技术研究所，上海 201109）

0 引言

现如今各类气象卫星、环境监测卫星、资源探测卫星等的在轨探测手段越来越全面，探测精度要求不断提高[1]。为保证卫星在轨探测的高精度、高稳定度，必须确保卫星在轨具有良好的姿态稳定度。作为卫星对地探测的重要有效载荷，星载辐射计向大型化、复杂化、多样化发展。其中，旋转式星载辐射计由于其自身转动部分结构的不规则性，转动部分质心无法完全与旋转中心重合，故在轨扫描转动时会对卫星的姿态稳定产生干扰，影响卫星探测精度，严重的甚至可造成卫星在轨倾覆，带来不可估量的损失。因此，在带有旋转部件的星载辐射计研制过程中往往需要对其进行动平衡设计和控制，以减小星载辐射计扫描转动时的动不平衡量，进而降低对卫星的干扰，提高卫星的姿态稳定度和在轨探测精度。

本文概述星载辐射计动平衡技术的研究应用，探讨和展望其发展趋势，并提出在轨动平衡技术的初步研究设想，以期为今后类似旋转式星载辐射计的动平衡设计、动平衡控制方法提供一定参考依据，为我国星载辐射计动平衡技术发展提供支撑。

1 星载辐射计动平衡技术概述

动平衡的概念最早出现在转子动力学领域，主要是用以减少转子挠曲、振动和轴承动态反力，动平衡技术研究的目的是减小甚至消除转子的动不平衡[2]。为此，学者提出了多种动平衡理论，包括力平衡法、两平面影响系数法、模态平衡法及影响系数法等[3]。各种动平衡理论与实现方法在航空发动机、直升机旋翼[4]等领域得到了广泛应用。

航天领域中，星载辐射计的动平衡技术日益受到关注。在国外，美国的“深度撞击号”彗星探测器在研制过程中进行了动平衡测试。NASA 对其研制的全球降水测量卫星（GPM）搭载的星载辐射计全球微波成像仪（GMI）进行了动平衡方法优化和动平衡测试[5]，动平衡测试配平后GMI 的残余静不平衡量为17 kg·mm、残余偶不平衡量为22 000 kg·mm2。

在国内，星载辐射计动平衡技术近十几年经历了快速发展。“风云二号”卫星星载辐射计、“海洋二号”卫星微波辐射计、“风云三号”卫星星载辐射计以及各类微小卫星研制中，都进行了星载辐射计动平衡技术研究[6-9]，以提升产品的动平衡性能。随着星载辐射计动平衡技术研究的深入，星载辐射计动平衡特性影响因素的研究也更加全面，已经从单纯的地面动平衡测试配平发展为集动平衡测试配平、地面动平衡影响因素分析、空间环境动平衡影响研究等于一体的综合性动平衡技术研究。基于此类综合性动平衡技术的研究，星载辐射计的动平衡性能得到较大提升，某型号大型旋转式星载辐射计的动平衡性能从最初的残余静不平衡量17 kg·mm、残余偶不平衡量10 000 kg·mm2提升至残余静不平衡量1.5 kg·mm、残余偶不平衡量2500 kg·mm2。可见，我国的星载辐射计动平衡性能要求已高于NASA类似设备的性能指标。

动平衡机是转子动平衡技术发展的最初形式，是转子动平衡特性的直接测试部件。动平衡机研制历史可以追溯到19 世纪，1907 年，世界第一台平衡机首先被德国的拉瓦切克（Lawaczeck）制造出来；进入21 世纪，随着信息电子技术的快速发展，动平衡机的测量精度有了很大提高。目前，德国的申克（SCHENCK）公司、霍夫曼（HOFMANN）公司和日本的国际计测器株式会社（KOKUSAI）的动平衡机在国际上处于绝对领先的地位[5]。我国动平衡机行业的发展起步较晚，20 世纪50 年代，华中工学院成功研制了国内首台通用型动平衡机[10]。国内针对空间航天器低转速动平衡测试系统的研究直到21 世纪才有所发展，近些年在此方面研究比较成熟的有湖北孝感龙腾检测设备有限公司及北京东方科学仪器厂等。其中前者研制的低转速动平衡测试系统已广泛应用于国内大多数航天院所，图1为该公司2020 年研制的ZGT-200 型星载辐射计专用低转速动平衡测试系统，其测试精度已达到残余静不平衡量0.6 kg·mm、残余偶不平衡量250 kg·mm2，处于国内领先水平。

图1 ZGT-200 动平衡测试系统Fig.1 ZGT-200 dynamic balance test system

目前，国内外对星载辐射计地面动平衡技术的研究已相对成熟，动平衡试验方法较为完善，但动平衡测试系统的精度仍有待进一步提高，以减小星载辐射计地面动平衡配平后的残余不平衡量。

2 在轨动平衡技术的提出

星载辐射计地面动平衡测试主要是通过动平衡机测得星载辐射计转动时的动不平衡量，并根据测试结果在对应位置增加或减少配重块进行配平，以减小星载辐射计的动不平衡量。现有地面动平衡技术只能够提高星载辐射计地面测试状态的动平衡，无法对星载辐射计在轨可能出现的动平衡状态变化进行主动的适应性调节。随着卫星探测技术的快速发展，卫星探测精度大幅提高，对星载辐射计动平衡性能要求也越来越高。单纯依靠地面动平衡测试配平提高星载辐射计动平衡稳定性的传统方式将逐渐无法满足卫星及星载辐射计在轨长寿命、高精度、高稳定度的需求。一方面，部分大型旋转式、可展开式星载辐射计发射入轨后，为保证其展开机构的可靠性，相关活动部件设计时会留有一定间隙，因此，活动部件在轨解锁展开后无法与地面动平衡测试时展开到位的状态完全一致，而展开机构重复展开到位后精度的不一致会造成星载辐射计在轨动平衡状态的变化。例如，某型号星载辐射计地面动平衡配平后，整机残余动不平衡量为静不平衡量1.08 kg·mm、偶不平衡量1 137.5 kg·mm2；而其天线展开机构重复收拢展开后，整机残余动不平衡量变大为静不平衡量4.3 kg·mm、偶不平衡量4 538.6 kg·mm2。其动不平衡量增大的主要原因就是展开机构重复收拢展开到位精度变化。另一方面，受地面重力场和在轨复杂的热环境影响，星载辐射计在轨工作后势必会出现动平衡状态的变化。这种变化会随着辐射计在轨工作时间的延长而逐步加大，同时会随着后续星载辐射计空间结构机构的大型化、复杂化变得更加突出。

而在轨动平衡技术的发展，可以很好地弥补以上这些不足——通过在轨动平衡技术进行星载辐射计在轨动平衡调节，可以实时、精细化地减小星载辐射计在轨动不平衡，大大提高卫星在轨探测精度。后续星载辐射计动平衡技术将逐渐向地面动平衡试验和在轨动平衡技术综合作用发展，依托在轨动平衡技术根据在轨监测结果，对动不平衡变化进行实时补偿配平，支撑卫星在轨探测技术向着精度更高、性能更稳定发展。

2021 年，XX-5 卫星启动立项论证，用户初步提出的卫星姿态稳定度指标为0.2‰，相较于其上一代XX-3 卫星6‰的卫星姿态稳定度要求，精度提高近20 倍。据此，XX-5 卫星搭载的星载微波辐射计动不平衡量指标预期提高至静不平衡量小于0.25 kg·mm、偶不平衡量小于250 kg·mm2。而据现有数据的仿真分析，XX-3 卫星星载辐射计在轨长期工作后，空间重力变形、空间热变形会引起星载辐射计静不平衡量1 kg·mm、偶不平衡量1500 kg·mm2的动平衡变化。因此，仅通过地面动平衡配平是无法满足XX-5 卫星在轨应用需求的。目前，XX-5 卫星研制团队已经着手进行在轨动平衡技术的研究和方案论证，预计在2030 年左右实现在轨应用。

3 在轨动平衡技术研究

在轨动平衡技术的应用可以减小旋转式星载辐射计在轨动不平衡量，有助于推动旋转式星载辐射计向大型化、多样化发展。但同时，受制于卫星在轨能源资源的有限性，在轨动平衡系统应当尽可能轻量化，即星载辐射计在轨需要补偿配平的配重块质量应当越小越好。因此，星载辐射计研制过程中一般先进行地面动平衡试验，将其动不平衡量配平减小至一定范围内。具体情况可分为2 种：

一类是通过地面动平衡配平可将其动不平衡量配平至满足指标要求范围内，但在轨长期运行后动不平衡量会变大而超出指标要求。这类星载辐射计需首先在地面动平衡试验时将其动不平衡量配平至指标范围内；同时通过仿真分析和计算，评估星载辐射计在轨受重力、热环境影响可能带来的动不平衡变化量，根据评估结果进行在轨动平衡系统设计。

另一类是卫星指标要求很高的星载辐射计，仅通过地面动平衡试验无法将其动不平衡量配平至指标要求范围内。该类星载辐射计可先在地面动平衡试验时将整机动不平衡量配平至一个较小的值，以保证星载辐射计地面扫描转动测试过程中产品的安全性和可靠性；然后通过分析地面动平衡试验配平后星载辐射计动不平衡量与卫星指标要求的差值，以及仿真分析计算星载辐射计在轨受重力、热环境影响可能带来的动不平衡变化量，并根据综合评估结果进行在轨动平衡系统设计，以确保其在轨动平衡系统具备足够的调节能力将星载辐射计在轨动平衡配平至指标要求范围内。

理论上，只要在轨动平衡系统具有足够的能源资源和配平质量块，在轨动平衡技术就可以将星载辐射计在轨任意大小的动不平衡量实时调节至指标要求范围内，保证卫星在轨运行的高精度和高稳定度。工程上，星载辐射计地面动平衡试验配平与在轨动平衡系统的设计还需根据卫星总体的实际要求进行针对性的设计与指标分配。

星载辐射计在轨动平衡技术实现主要包含3 个步骤：首先通过卫星在轨实时响应测量系统测出星载辐射计的在轨动不平衡量，然后由在轨动平衡反馈系统将动不平衡量测量值实时反馈至卫星控制单元，最后由在轨动平衡调节装置根据控制指令进行星载辐射计配平面质量块的动态调整，从而实现在轨动平衡配平。

3.1 在轨动平衡配平技术方案

根据星载辐射计的一般结构形式，在轨动平衡配平方案考虑通过电动滑台对星载辐射计配平面上可移动的质量块进行位置调整，进而实现星载辐射计动平衡状态的调节，达到减小星载辐射计在轨动不平衡量的目的。针对质量块的布置及移动方式，初步考虑了直线导轨和圆形导轨2 种滑台布局方案，如图2 所示。

图2 质量滑块调整的滑台布局方案Fig.2 Slide table layout scheme of mass slider adjustment

由图2 可以看到，由于每次质量滑块发生移动后，质量滑块初始位置的反方向会产生1 个新的大小相等方向相反的不平衡量，因此需在配平面导轨上设置至少2 个质量滑块共同作用，才可消除配平面上的不平衡量，实现在轨动平衡实时调整。以下针对这2 种滑台布局方案进行在轨动平衡配平实施途径及理论探讨。

3.1.1 直线导轨配平技术方案

直线导轨方案主要考虑在星载辐射计配平面上靠近外侧合适位置布置2 条相互垂直且与星载辐射计产品坐标系正交的长度为L的直线导轨，导轨法向距星载辐射计转动中心轴距离为r，如图3所示。将图中坐标系X轴的正方向定义为转动0 位，假设竖直导轨上质量滑块的质量为m1，初始位置与X轴的夹角为θ01；水平导轨上质量滑块的质量为m2，初始位置与Y轴的夹角为θ02；星载辐射计转动过程中测得转动半径为r处的动不平衡量大小为M、相位角为α。（为方便后文叙述计算过程，本文直接以m1、m2同时指代两滑块及其质量。）

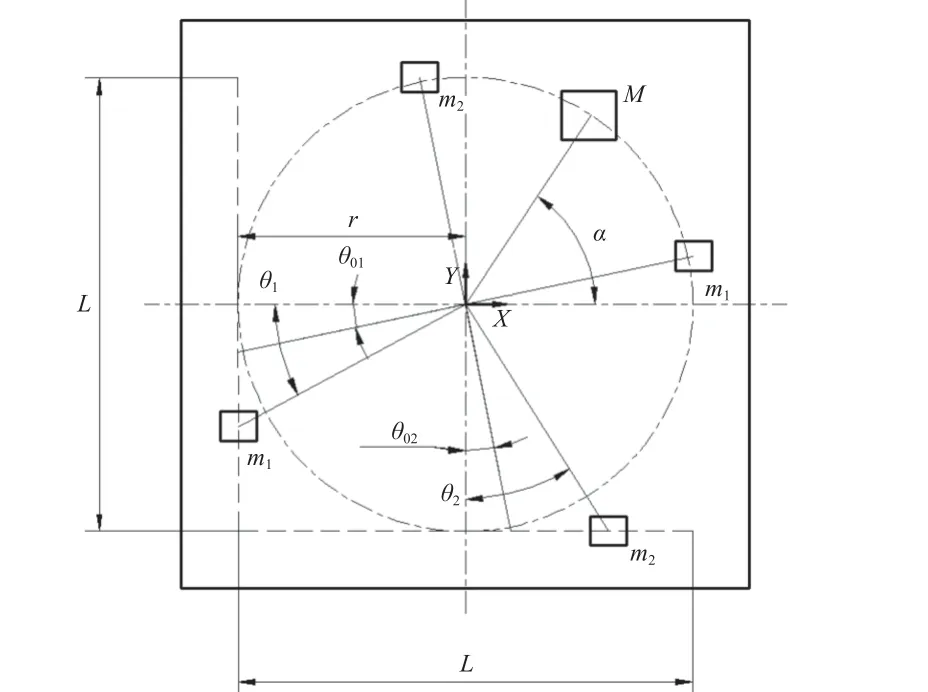
图3 直线导轨方案质量滑块调整示意Fig.3 Linear guide schematic of mass slider adjustment

根据动平衡配平要求，2 个质量滑块需分别移动到指定配平位置，使星载辐射计的动不平衡量为0。假设质量滑块m1、m2移动到指定配平位置后与X、Y轴的夹角分别为θ1、θ2，这2 个质量滑块产生移动后在其移动前的初始位置反向也会分别产生相等大小的不平衡质量m1、m2。因此，质量滑块m1、m2移动到指定配平位置后形成的新的动平衡稳定状态为这5 个质量块共同作用实现的。

根据图3 中不同质量滑块的位置示意，列出X、Y两个正交方向的平衡方程，

对式(1)进行化简求解，得到θ1、θ2的解，

式中，m1、m2、θ01、θ02为已知量，M、α为在轨动平衡测试系统实测值，θ1、θ2为变量。求得θ1、θ2即可得到质量滑块m1、m2需移动到的指定配平位置，进而实现星载辐射计在轨动平衡配平。

3.1.2 圆形导轨配平技术方案

圆形导轨方案主要考虑在星载辐射计配平面上距转动中心距离为r的位置圆周方向布置360°范围的圆形导轨，在圆形导轨上放置2 个质量块。假设圆形导轨上质量滑块的质量分别为m1、m2，初始位置与X轴的夹角分别为θ01、θ02；星载辐射计转动过程中测得转动半径为r处的动不平衡量大小为M、相位角为α，如图4 所示。

与直线滑轨原理相同，根据动平衡配平要求，2 个质量滑块需分别移动到指定配平位置，使星载辐射计动不平衡量为0。假设质量滑块m1、m2移动到指定配平位置后与X轴的夹角分别为θ1、θ2，这2 个滑块产生移动后在其移动前的初始位置反向也会分别产生相等大小的不平衡质量m1、m2。因此，质量滑块m1、m2移动到指定配平位置后形成的新的动平衡稳定状态同样为这5 个质量块共同作用实现的。

根据图4 中不同质量滑块的位置示意，列出X、Y两个正交方向的平衡方程，

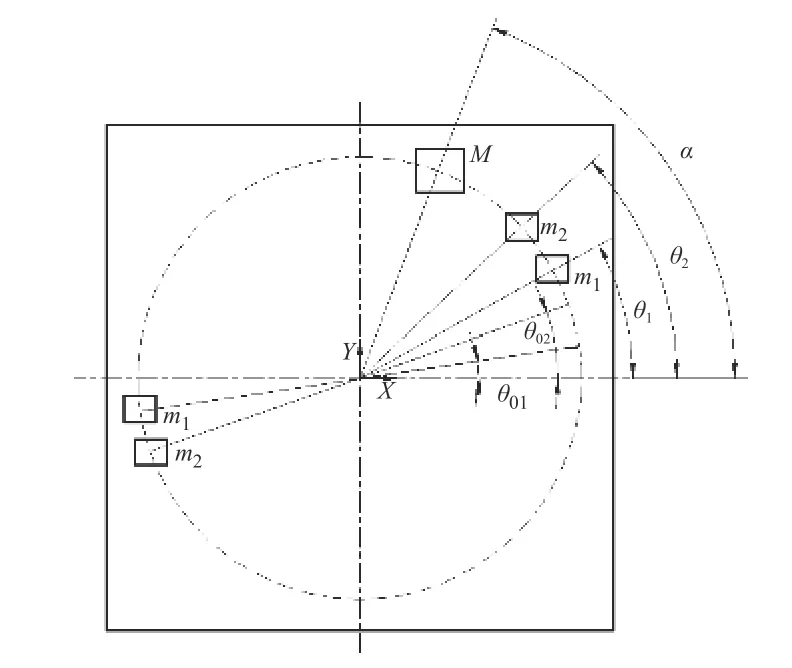
图4 圆形导轨方案质量滑块调整示意Fig.4 Circular guide schematic of mass slider adjustment

对式(3)进行整理，无法完全分离出变量θ1、θ2，仅能表达量之间相互关系，

式中，m1、m2、θ01、θ02为已知量，M、α为在轨动平衡测试系统实测值，θ1、θ2为变量。通过对式(4)求解，可得到质量滑块m1、m2需移动到的指定配平位置，进而实现星载辐射计在轨动平衡配平。

3.1.3 小结

通过对上述2 种导轨布局进行对比分析发现，直线导轨方案构型更简单，也更易于实现，但其滑块的滑动范围有限，可能存在方程无解的情况，即两滑块在直线导轨上有限的移动范围内无法移动到指定配平位置，出现无法实现配平的盲区。圆形导轨滑动范围更大，理论上对于任意不平衡量都存在配平位置，但该方案的轨道结构布局和滑块驱动机构设计都相对更为复杂。因此，实际工程应用还需根据星载辐射计产品的具体结构形式、在轨动平衡指标要求、导轨布置方式、滑块驱动机构设计等进行综合考量，选择适合的方案。

3.2 在轨动平衡测量技术

为实现星载辐射计在轨动平衡，一个关键环节是要能够对星载辐射计在轨扫描转动所产生的动不平衡量进行精准的实时测量。在轨动平衡测量技术的核心是测出星载辐射计转动过程中由其动不平衡带来的干扰力；然后通过相应的专业理论基础和求解换算，计算动不平衡量。测量方法有2 种，一种是通过传感器直接测量干扰力，另一种是通过陀螺仪测量卫星转角信息间接获取。

通过传感器直接测量的方法原理上相对简单，可在星载辐射计与卫星本体连接的安装面处安装传感器，通过传感器直接测得的干扰力以及传感器安装位置与星载辐射计质心相对位置关系，求解星载辐射计的动不平衡量，整个测量及转化过程的复杂度较低。

通过陀螺仪测量卫星转角信息获取星载辐射计在轨扫描转动不平衡量的方法相对复杂，需分别测量星载辐射计关机静止状态和开机稳速扫描转动状态下卫星绕俯仰轴的转角-时间数据，对转角数据进行时域上2 次求导，得到卫星角加速度-时间数据；再将星载辐射计关机与开机状态下测得的卫星角加速度求差，此差值即由星载辐射计开机扫描转动后不平衡量引起的。卫星角加速度随时间周期性变化，最大值出现在星载辐射计干扰力方向与卫星俯仰轴夹角为90°时。

假设星载辐射计开/关机状态下的转角差为Δθ，卫星绕俯仰轴的转动惯量为I22.s，卫星绕俯仰轴的力矩为M22.s，星载辐射计扫描转动过程产生的干扰力为Fm，扫描转动周期为Tm，星载辐射计质心与卫星质心在偏航轴向上的投影距离为L。则，星载辐射计转动引起的卫星角加速度增量与卫星绕俯仰轴力矩增量间的关系为

根据动平衡测量原理，由星载辐射计动不平衡量产生的干扰力为

将式(6)代入式(5)可以得到星载辐射计动不平衡量为

综上，通过力传感器测量星载辐射计动不平衡量的方法原理上更为简单，传递误差也较小，但需在星载辐射计安装面合适位置布置一套高精度传感器检测系统，还需综合考虑星载辐射计结构形式、与卫星安装位置关系等影响因素。通过陀螺仪测量卫星转角信息获取星载辐射计动不平衡量的方法不需要增加额外硬件测试设备，仅通过卫星原有的姿轨控系统就能够实现，但存在测量干扰较多、多级换算传递误差大等劣势。

3.3 在轨动平衡实时调整反馈控制系统设计

为对星载辐射计在轨扫描转动时的动平衡状态进行实时测量和闭环控制，在轨动平衡实时调整反馈控制必不可少。控制系统以在轨动平衡实时测量系统测得的星载辐射计动不平衡量作为控制输入，通过控制器内响应控制算法的处理解算，分配质量分布调整的最优控制指标，驱动质量滑块相应执行机构进行在轨动平衡配平，并将配平后输出的残余动不平衡量反馈给实时闭环控制，控制系统框图如图5 所示。

图5 在轨动平衡实时调节反馈控制系统框图Fig.5 Block diagram of real-time adjustment feedback control system for on-orbit dynamic balance

应针对在轨动平衡调整反馈控制系统“快、准、稳”的要求，以星载辐射计动平衡指标为基础，结合在轨动平衡实时测量系统采样频率、质量滑块系统滑轨驱动参数等指标，设计合理的在轨动平衡实时调整反馈控制系统，同时需满足系统响应时间、峰值时间、超调量、稳态误差等各项指标要求。

4 结束语

本文对星载辐射计动平衡技术研究现状进行阐述，提出在轨动平衡技术应用需求和技术优势。初步探讨了星载辐射计在轨动平衡技术，包括在轨动平衡配平技术方案、在轨动平衡测量技术、在轨动平衡实时调整反馈控制系统设计，可为今后旋转式星载辐射计在轨动平衡技术研究及在轨工程实现提供一定的参考依据。

目前，国内外星载辐射计动平衡技术还处在地面动平衡理论和测试技术研究从低精度向高精度转变的过程。随着今后卫星探测技术的快速发展，星载辐射计动平衡技术势必会成为航空航天领域一个长久研究课题，在轨动平衡技术将成为星载辐射计在轨动平衡控制的发展趋势，也有望尽快实现型号在轨工程应用。