声学超表面抑制高速边界层内宽频不稳定模态研究

王蔚彰，孔维萱，严昊，赵瑞，*

(1.北京理工大学宇航学院，北京 100081；2.北京航天长征飞行器研究所，北京 100076)

在高超声速的飞行工况下，飞行器壁面的层流极易发展为湍流，该过程即为转捩[1]。转捩会使得飞行器壁面摩阻和壁面热流显著增加，从而使得飞行器载重比减小，燃油效率降低等。转捩问题是经典力学遗留的少数基础科学问题之一，与湍流问题一起被称为“百年难题”。随着高超声速飞行器的不断发展，有效控制高超声速边界层转捩愈发重要，进而降低飞行阻力，减小壁面热流，提高燃料效率[2-5]。目前的转捩控制技术可分为两大类：①主动控制技术，如壁面吹吸、等离子激励、二氧化碳注射等，由于需要在飞行器外部增设运行机构，不便应对高超声速飞行工况下严峻的气动力热环境，很难投入到实际工程应用当中；②被动控制技术，如粗糙元、波纹壁、声学超表面等，由于其机构设置简单，具有较高实用前景。其中声学超表面特征尺度（孔径）远小于边界层厚度，对基本流影响较小。由于声学超表面具有各种不同的材料特性和微结构形式，可通过多种作用机理影响转捩，应用前景更加广泛[6-8]。

对于可压缩流动，边界层内扰动可以分为快声波、慢声波、熵波和涡波。快、慢声波是相对自由流以声速传播的扰动，假设自由流的马赫数为Ma，则快、慢声波的无量纲相速度分别为c=1±1/Ma，可分别激发出快/慢(F/S)模态，主要区别在于相速度，在流场前端，F 模态的相速度趋近于1+1/Ma，S 模态的相速度趋近于1−1/Ma。快模态向下游发展到某个流向位置处时，其与慢模态相速度的实部相同，这个位置被称为同步点。同步点之前，慢模态为第1 模态；同步点之后，慢模态为增长率较高的第2 模态[9-11]。

Fedorov 等[2]最早使用线性稳定性理论[12]（linear stability theory,LST）研究了规则微型圆孔超表面对第2 模态的抑制效果，并在高超声速尖锥风洞试验中证实了声学超表面能够显著延长层流区域[13]。涂国华等[14]基于Fedorov 的方法探索了多孔超表面的最优开孔率和孔半径，Zhao 等[15]考虑了相邻孔之间的干扰，提出了具有更高预测精度的超表面阻抗模型，并采用直接数值模拟方法（directnumerical simulation，DNS）详细分析了扰动与微结构相互作用演化过程[16-17]。郭启龙等[18]对较大尺寸的横向矩形微槽进行了数值模拟，研究表明横向微槽在一定宽带频率范围内对第2 模态有明显的抑制作用，且开槽率越大，抑制效果越好，其中开槽率 φ=ns/L，n为开槽数，s为微槽宽度，L为整个开槽表面的流向长度。Tu 等[19]通过对比分析天地工况下的稳定性，发现钝度雷诺数对转捩N值影响较大，给出多个经验关系式，提高转捩预测精度。刘强等[20]对高超声速边界层的主要失稳机制进行了概述，分别从主动和被动控制2 个方面详细介绍了延迟转捩控制技术的最新进展。

但是Fedorov 等[21]针对金属毡的实验研究发现，声学超表面在抑制第2 模态的同时，会引发第1 模态的不稳定性，并且该不稳定性随着壁面温度的下降而减弱。Wang 和Zhong[22-23]发现声学超表面的放置位置及导纳相位角对边界层稳定性的抑制效果均有一定影响。Tian 等[24]提出一种反向设计方法，在马赫数为4 边界层流动中有效抑制第2 模态，同时不显著激发第1 模态，然而这种设计方法需要沿流向渐进改变微结构几何尺寸，不易加工实现。更重要的是，在该马赫数下，同时存在第1 模态和第2 模态，需要综合考虑。随后，赵瑞等[25]针对第1 模态进行了声学超表面的设计，实现了在单频和宽频下抑制第1 模态的目的，但未考虑对第2 模态的影响。

实际工程应用中，声学超表面在抑制边界层转捩主导模态的同时，应避免激发另一模态诱发转捩，这样才能有效延长层流覆盖区域。基于该目的，本文以马赫数为4 的超声速边界层为研究对象，使用LST 研究了声学超表面导纳相位与幅值对各扰动模态的影响规律，提出一种工程可实现的声学超表面设计方案。在综合考虑第1 模态和第2 模态的前提下，能够实现宽频扰动抑制。

1 研究方法与模型

1.1 线性稳定性理论

用线性稳定性分析[26-29]研究可压缩黏性流体高超声速边界层中的不稳定性问题。

设扰动量 ϕ为

将瞬时量表示为平均流和扰动量之和，代入可压缩黏性流体的雷诺平均Navier-Stokes 方程和气体状态方程可推导出扰动的控制方程为

式中：C为五阶矩阵；Fn为非线性项。

将式(1)代入式(2)中，忽略非线性项，可得

式中

基于平行流假设，流向的导数项可忽略不计，式(3)可简化为

边界条件为

式中：A为 声学超表面的导纳。导纳A为声阻抗的倒数，其值取决于材料特性、孔隙参数及扰动参数等。对于光滑壁面， |A|=0。声阻抗为声压与声流量之比，表示声波在介质中传播时需要克服的阻力。

联立式(4)和式(5)，通过数值方法求解得到 α,虚部为 αi，则扰动波的增长率 σ=−αi。 若 α＆gt;0，即增长率 σ＆lt;0,则表示扰动波处于不稳定状态，本文采用 σ表征扰动波的增长率大小。

1.2 e N 方法

eN方法是基于线性稳定性理论，通过累计不稳定波的线性增长率来预测转捩的一种半经验方法[30]。边界层内的小扰动逐步向下游传播，进入不稳定区域后扰动的幅值会被逐步放大。沿扰动传播的方向对增长率积分，可以得到幅值的放大倍数为

式中:x0为 积分起始位置；x为任意流向位置。

通常根据实验或经验设定一个转捩判据NT，当N达到NT时认为转捩发生。实际流动中，有多种不同频率的小扰动，可计算得到一族不同频率下的转捩判据N值曲线，取该族曲线的包络线，当N值包络达到NT时，对应的位置认定为转捩发生位置，即转捩位置与N值包络应满足：

其直接连接了转捩位置xtr与 起始位置x0处扰动的振幅比关系，可以写为

1.3 缝隙型超表面的阻抗模型

假设来流为理想气体，普朗特数Pr=0.72，比热比 γ=1.4。来流条件与文献[24]相同，即来流马赫数Ma=4，单位雷诺数Re=1.39×107，来流温度=70.238K，板长为0.4m。平板壁面为等温壁2= 9 5 K，上标*表示参数有量纲，边界层外缘参数用下标e表示。动力黏性系数 µ∗通过Sutherland 定律求得。速度u∗和v∗、 动力黏性系数 µ∗、 温度T∗和 密度 ρ∗分别以边界层边缘处的速度和进行无量纲化。压力p∗、 流向波数 α和 无量纲角频率 ω分别以、 1/l∗和/l∗作 为量纲,其中无量纲角频率ω=2πf∗l∗/，其中，

如图1(a)所示为缝隙型超表面在xOy面内的二维切面， −y方向为孔深方向。缝隙的孔宽为 2b，孔深为H，周期为s。 对应的孔隙率n=2b/s， 宽深比Ar=2b/H。x、y及长度等变量通过l∗进行无量纲化。图1(b)为缝隙型超表面的三维结构示意图。

图1 缝隙型声学超表面的示意图Fig.1 Schematic diagram of the aperture type acoustic metasurface

缝隙型声学超表面的导纳式[24]为

式中：kv和kt分别为无量纲黏性波数和热波数。

A=|A|eiθ|A|

导纳A可表示为 。其中 为导纳幅值， θ（实数）为导纳相位。每单位面积的声学超表面对扰动能量的影响为

式中：c.c.为相应的共轭复数；下标w 为壁面参数。

由于声学超表面微结构对扰动波的黏性耗散作用，Ew＆lt;0。因此，相位 θ 的取值范围是0.5 π～1.5 π。

2 声学超表面设计

2.1 导纳对扰动模态的影响

如图2 所示为光滑平板表面的线性稳定性分析结果，从图2 中可以看出，在宽频范围下，平板边界层中同时存在第1 模态与第2 模态，且较小的无量纲角频率 ω对应为第1 模态，较大时对应第2 模态。随着流向位置x的变化，第1 模态和第2 模态增长率大于0 所对应的 ω范围基本不变，第1 模态在ω范围为0.03～0.12 内增长率大于0，第2 模态在 ω范围为0.23～0.27 内增长率大于0。因此，可以采用无量纲角频率 ω表示第1/第2 模态的不稳定性性质，与文献[24-25]结论相同。

图2 光滑平板表面不稳定模态的增长率Fig.2 Growth rates of unstable modes on smooth solid walls

以x=0.2m 处为例，进一步研究声学超表面导纳相位 θ变化范围：0.5 π～1.5 π，幅值 |A|变化范围为：1～8，对边界层中的第1/第2 模态增长率的影响规律。从图3(a)中可以看出，导纳相位 θ= 0.5 π时，第1 模态可被抑制，但同时，第2 模态会被激发；从图3(b)中可以看出，相位 θ 为0.75 π时，第2 模态受到抑制，但同时，第1 模态会被激发；且相位 θ越接近 π，对第2 模态的抑制效果越好，其中图3(c)给出了 θ 为 π的 结果。整体来看，幅值 |A|越大，对不稳定模态的抑制/激发效果越明显。

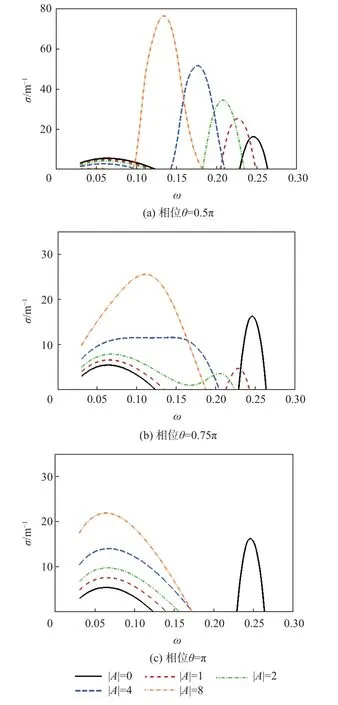
图3 声学超表面导纳相位与幅值对不稳定模态增长率的影响Fig.3 Effects of admittance phase and amplitude of acoustic metasurface on the growth rates of unstable modes

如图4 所示，以ω=0.12 表征第1 模态，此时光滑表面的增长率 σ=0.62，固定导纳幅值等于2，研究导纳相位对第1 模态增长率的影响。从图4 中可以看出，当θ ＆lt;0.55 π时，声学超表面可以对第1 模态产生抑制效果。

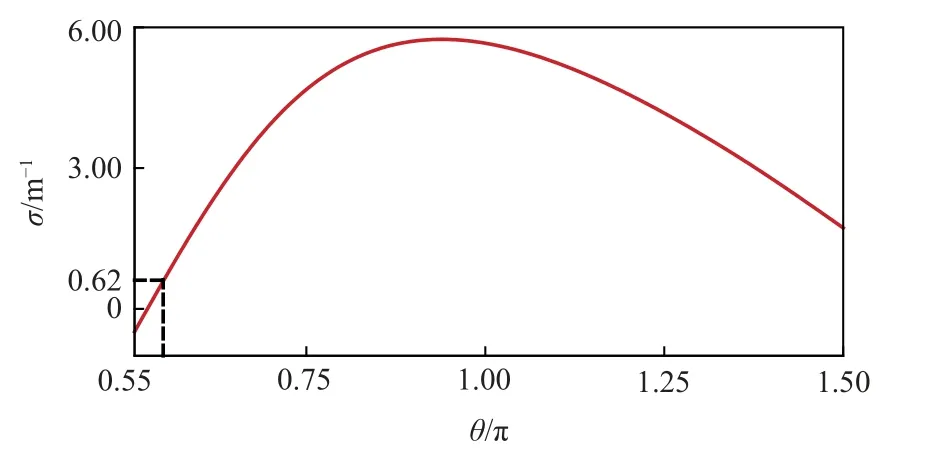
图4 不同导纳相位对第1模态增长率的影响Fig.4 Effects of admittance phase on the growth rates of the first mode

对于相位 θ 接近0.5 π的情况，在一定频率范围内（ ω ＆lt; 0.12），导纳幅值 |A|的增大可以增强对第1 模态的抑制效果，但会增强对第2 模态的激发效果，并导致不稳定第2 模态的频率降低，甚至在同一频率下同时出现不稳定的第1 模态和第2 模态。因此对于本文算例，当ω为0.03～0.12 之间时（即第1模态），导纳相位尽量接近0.5 π，可抑制第1 模态；在ω为0.23～0.27 之间时（即第2 模态），导纳相位大于0.75 π，可抑制第2 模态；且在ω为0.12～0.23之间时（第1/第2 模态重叠区域），尽可能使导纳幅值较小，可减弱对第2 模态的激发效果。总之，通过在不同频率范围内调节导纳相位和幅值，可实现宽频范围下抑制边界层第1/第2 模态扰动波。

2.2 微缝隙几何参数对导纳的影响

通过2.1 节可获得导纳相位和幅值对边界层内不稳定模态的影响规律，进一步研究超表面微结构几何参数对导纳相位和幅值的影响，以期通过调整几何参数获取目标导纳。如图1 所示，超表面主要参数有孔隙率n（0.1～0.8），宽深比Ar（0.1～1.5），深度H（0.1～2mm），分别研究宽频范围下各参数对导纳的影响。

2.2.1 孔隙率n

保持宽深比A r=1.5，深度H=0.5mm 固定不变，孔隙率n在0.1～0.8 区间内变化。如图5（a）所示，固定ω下孔隙率对导纳相位没有影响，随着ω的增加，导纳相位从小到大逐渐增加；在导纳相位增长较快的频率区域，导纳幅值较大，并且随着孔隙率n的增大而增大（见图5（b））。在深度增加后，基本变化规律不变，导纳相位从小到大不断往复。

图5 孔隙率对导纳相位和导纳幅值的影响Fig.5 Effect of n on admittance phase and amplitude

2.2.2 宽深比A r

保持孔隙率n=0.5，深度H=0.5mm 固定不变，宽深比Ar 在0.1～1.5 区间内变化。如图6（a）所示，横向来看，随着Ar 的增加，导纳相位在不同ω下呈单调变化，变化幅度较小；纵向来看，Ar 较小时，导纳相位接近 π，且在宽频范围内的变化幅度较小；Ar 较大时，导纳相位在宽频范围内从小到大逐渐增加；在导纳相位增长较快的频率区域，导纳幅值较大，且随着宽深比Ar 的增大而增大（见图6（b））。结合2.1 节的研究可得，在较低频率下（0.03＆lt;ω＆lt;0.12），导纳相位应小于0.55 π，才可抑制第1 模态，因此Ar 需大于等于0.7；并且随着宽深比的增加，导纳相位等于0.55 π时对应的幅值逐渐增大。

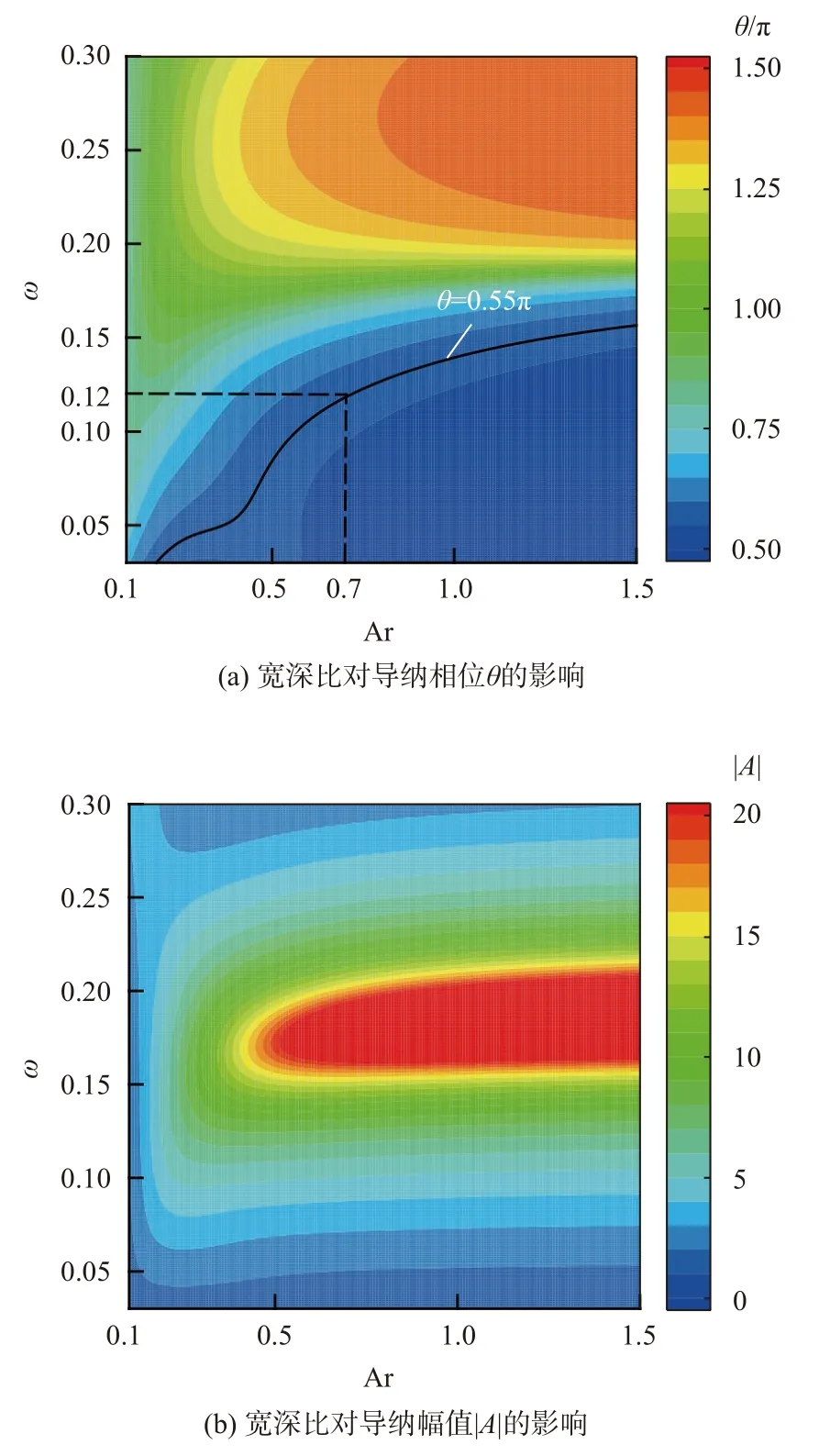
图6 宽深比对导纳相位和导纳幅值的影响Fig.6 Effect of Ar on admittance phase and amplitude

2.2.3 深度H

保持n=0.5，Ar=1.5 固定不变，深度H 在0.1～2mm 区间内变化。图7 为不同孔深的二维缝隙声学超表面在宽频范围下导纳的变化规律。从图7中可以看出，当孔深H＆lt;0.2mm 时，随着ω的增加，导纳相位基本保持在0.55 π以下，导纳幅值略微增加；当0.2mm＆lt;H＆lt;1 mm 时，随着ω的增加，导纳相位从0.5 π增加至1.5 π，同时导纳幅值也会先增加再减小，并且发现导纳相位在0.55 π～ 1.2 π之间变化十分明显，同时导纳幅值在该阶段内处于极大值；当H＆gt;1 mm 时，导纳相位和导纳幅值则会反复增加和减小。结合2.1 节研究可得，在较高频率下（ω＆gt;0.23），为抑制第2 模态，导纳相位应大于0.75 π，因此，深度H应限制在0.1～1mm 之间；在第1/第2 模态重叠区域（0.12＆lt;ω＆lt;0.23）,由于第2 模态在导纳相位处于0.55 π～ 0.75 π范围内且导纳幅值较大时，增长率会被剧烈激发，并且该阶段无法避免，因此需要保证导纳幅值尽可能小。

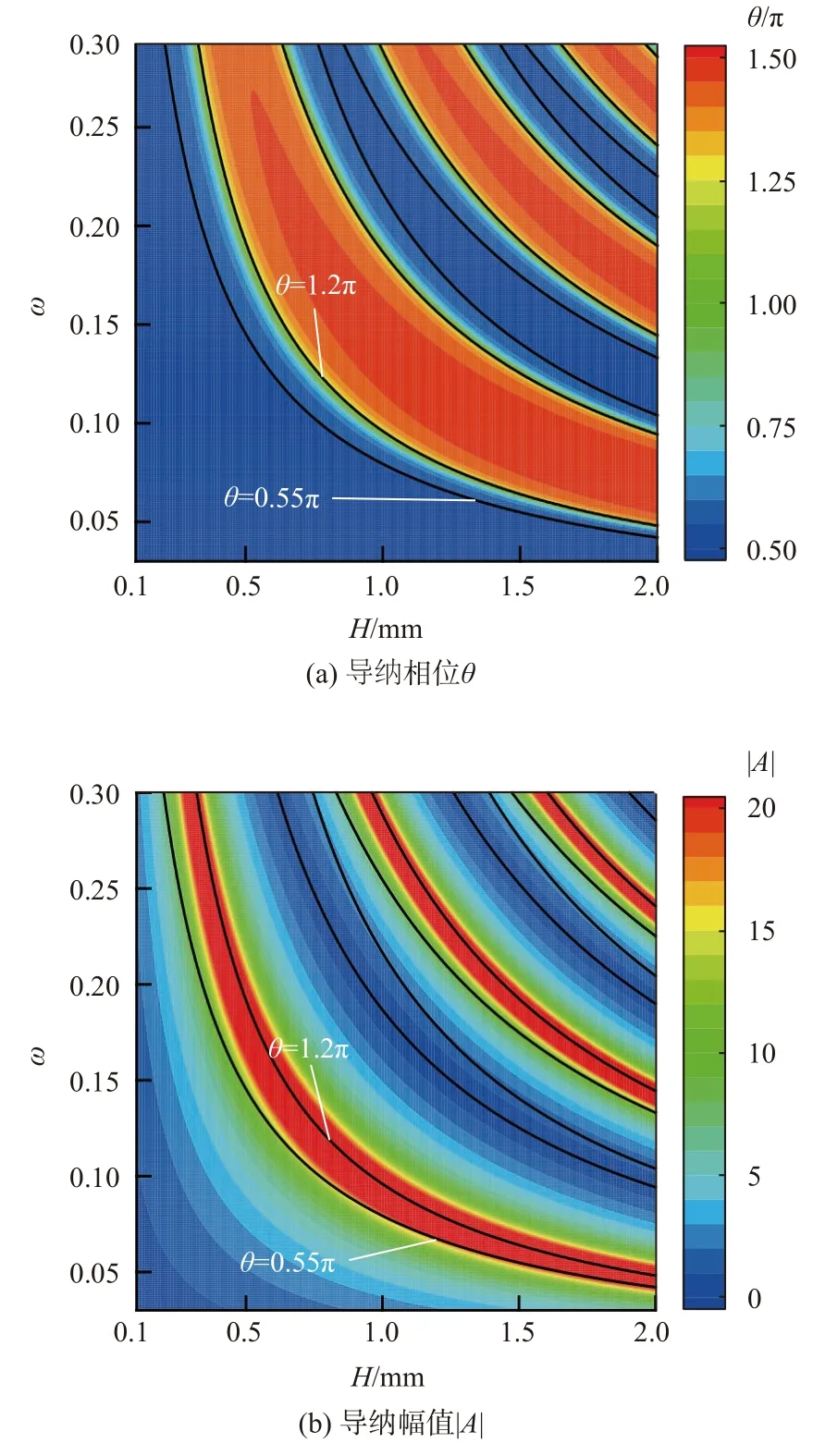
图7 深度对导纳相位与导纳幅值的影响Fig.7 Effect of H on admittance phase and amplitude

2.3 可实现性宽频抑制方案

对于同时存在第1 模态和第2 模态的边界层流动，在进行声学超表面微结构设计时，需要同时考虑2 种模态。在马赫数为4 的来流条件下，同时存在第1 模态和第2 模态，因此，既需要以抑制第1模态为目标进行声学超表面的优化设计，又需要兼顾不过分激发第2 模态甚至抑制第2 模态。

根据2.1 节的研究可得筛选二维缝隙参数的方法为：

1)ω＆lt;0.12 时，导纳相位小于0.55 π，且导纳幅值较小，可保证对第1 模态的抑制效果；

2)在第1/第2 模态重叠的频率区域，需要取导纳幅值最小对应的参数，可尽量减小对第2 模态的激发效果；

3)ω＆gt;0.23 时，导纳相位大于0.75 π，可保证对第2 模态的抑制效果。

根据2.2 节的研究可得微缝隙几何参数域为：孔深H(0.1～1mm)、孔隙率n(0.1～0.8)和宽深比Ar(0.7～1.5)。在不同x位置处，通过在参数域中进行循环筛选得出抑制效果最优的缝隙参数，并且保证所筛选出的参数符合式(9)使用条件：s＆lt;λ，其中s为缝隙周期长度， λ为扰动波波长。

根据如图8 所示的流程进行筛选缝隙几何参数。

图8 缝隙参数筛选流程Fig.8 Flow chart of slit parameter screening

经筛选得到的不同流向位置处的最优缝隙参数，如表1 所示。其中宽深比Ar 均为0.7，为筛选参数域内的最小值，这是由于宽深比增加会导致对应导纳幅值增大，与2.2 节中的结论相吻合；孔隙率不是最小值，同时逐渐增加，这是由于需要保证缝隙参数满足式(9)使用条件：s＆lt;λ；n和Ar 保证了导纳幅值最小，减小了第1/第2 模态重叠区域的激发效果，深度H不断增加则保证了不同流向位置处对低频第1 模态和高频第2 模态的抑制效果。

表1 不同 x 位置处的最优缝隙参数Table 1 Optim al gap parameters at different x positions

经多项式拟合深度后得：H=0.1525+1.49356x−0.50379x²。依据拟 合式，分别设计2 种声学超表面：①从0.05m 处开始，每0.0 1m 通过拟合公式给定新的孔隙参数进行分段，总计35 段，记为声学超表面A；②进一步提高工程上的可实现性，从0.05m处开始，每0.02m 分为一段，总计17 段，记为声学超表面B。

2.4 线性稳定性分析

使用LST 对声学超表面A 宽频扰动抑制效果进行分析（超表面B 结果类似，此处不再赘述）。如图9(a)所示，分段设计后的声学超表面A 可对40～80 kHz 范围内的扰动，即第1 模态实现宽频抑制效果；如图9(b)所示，对于160～240 kHz 范围内的扰动，即较低频率的第2 模态，声学超表面可使其最大增长率位置前移，但不被过分激发;如图9(c)所示，对于320～400 kHz 频率范围内的扰动，即高频第2 模态，其作用范围较小，处于x在0.05～0.1m之间，在该范围内可实现良好的宽频抑制效果。

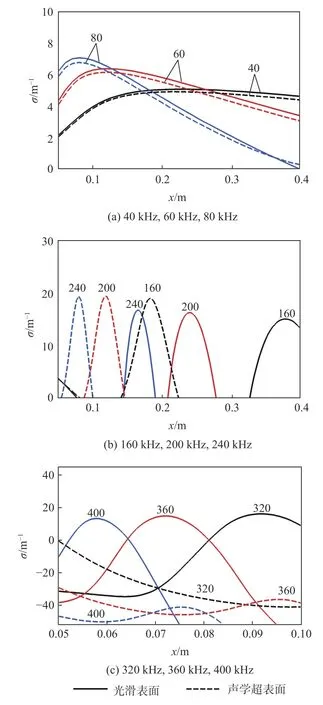
图9 不同频率下扰动模态在声学超表面与光滑表面的增长率对比Fig.9 Growth rates of unstable modes at different frequencies on acoustic metasurface and smooth surface

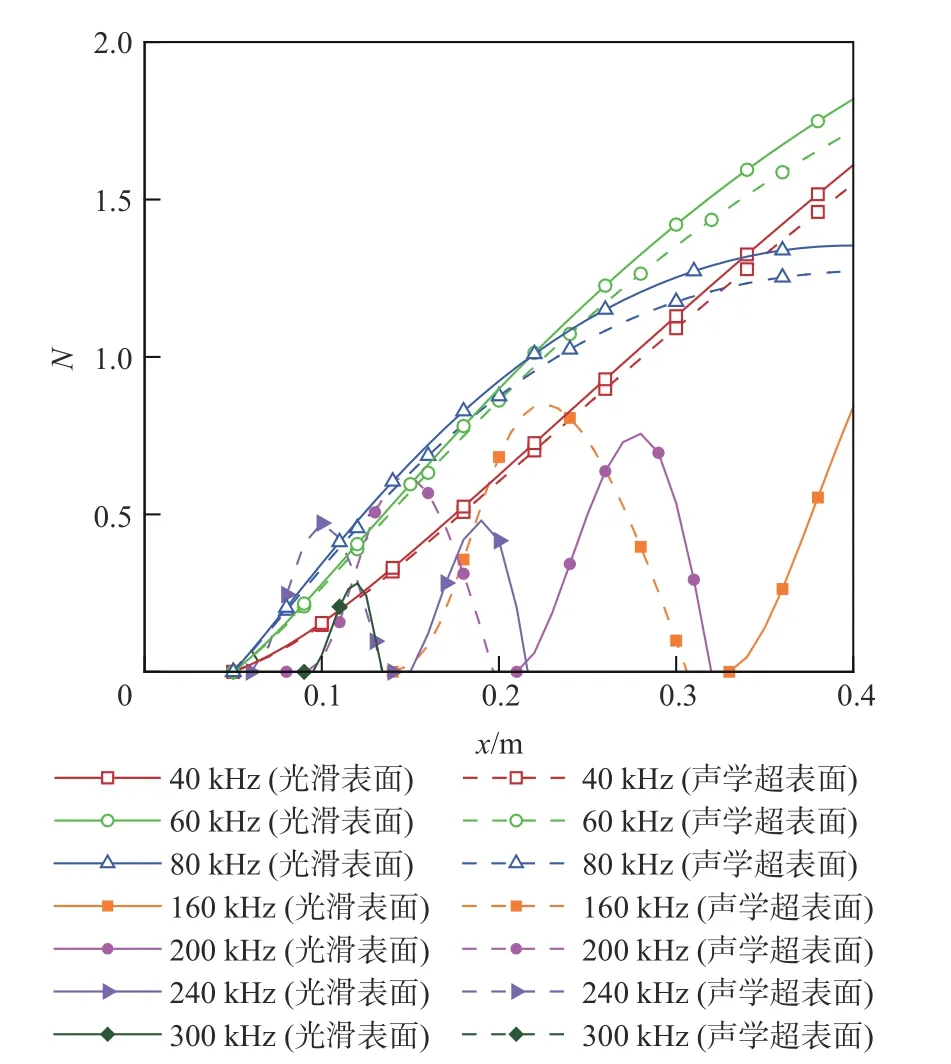
图10 声学超表面与光滑表面的N值曲线对比Fig.10 Comparisons of N-value curves of acoustic metasurface and smooth surface

如图11 所示，由声学超表面与光滑表面的 eN包络线对比可得，声学超表面均使平板前端的N值增加，平板后端的N值减小。在N=1.82 时，光滑表面对应的x位置为0.4m，声学超表面对应的x位置为0.436m，要比光滑表面延迟约9.24%。在相同流向位置x=0.4m 处时，声学超表面的N值为1.71，相比于光滑表面减小6.04%。相比于声学超表面A，声学超表面B 由于分段数较少，对低频第2 模态的前移与激发效果更明显，使得平板前端N值增加的程度与范围更大；由于对第1 模态的抑制效果基本相同，使得2 种声学超表面在平板后端的N值基本不变。

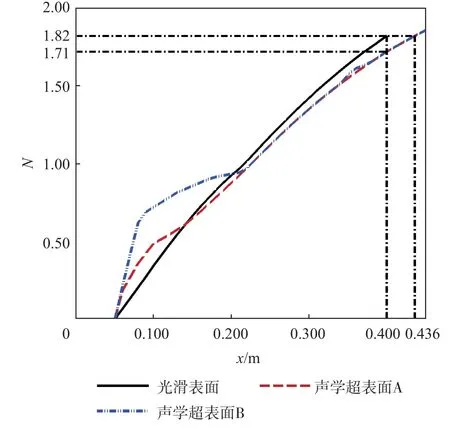
图11 声学超表面与光滑表面N值包络线对比Fig.11 Comparisons of N-value envelopments of acoustic metasurface and smooth surface

3 结 论

本文使用LST 计算分析了声学超表面的导纳对超声速平板边界层中第1 模态和第2 模态的影响规律。在Ma为4 的工况下，结合缝隙几何参数对导纳的影响，提出一种可实现性宽频抑制的分段设计方案，并采用 eN方法对声学超表面进行验证，结果如下：

1）当导纳相位减小至0.5 π时，第1 模态可被抑制，但第2 模态会被激发；与此同时导纳幅值在部分频率范围内增大时，抑制第1 模态的效果更加显著，一旦超出该范围会激发第1 模态；当导纳相位接近 π时，第2 模态受到抑制，但第1 模态会被激发；整体来看，幅值越大，对不稳定模态的抑制/激发效果越明显。

2）宽频抑制方案的声学超表面可以在宽频范围内同时抑制第1 模态和高频第2 模态，且不过分激发低频第2 模态。

3）声学超表面使得平板前端N值略有增加，平板后端N值降低；在到达相同N值时，声学超表面对应的x位置要比光滑表面延迟约9.24%。

本文提出的可实现性宽频抑制方案针对Ma为4 的工况下第1 和第2 模态，忽略更高阶的模态影响。在此基础上，后续将使用直接数值模拟对所优化设计的缝隙型声学超表面进行验证，并与LST结果进行对比分析，进一步研究声学超表面的工程应用价值。对于其他工况与更高阶的模态，可采取类似的分析方法进行优化设计。