曲线纤维壁板屈曲/后屈曲建模与快速分析方法

王泽溪，万志强，王晓喆，杨超

(1.北京航空航天大学航空科学与工程学院，北京 100191；2.北京航空航天大学无人系统研究院，北京 100191)

复合材料层合板具有明显的质量优势，已经被现代飞行器结构广泛使用[1]。现代飞行器对于结构减重具有迫切需求，复合材料具有比强度高、比刚度大、可设计性强等优势[2]，在新研飞机上的应用比重也越来越高，如大型民用飞机Boeing787，其复合材料结构质量占到了全机结构质量的50%[3]。传统直线纤维复合材料层合板承受面内压缩和剪切载荷时易发生失稳破坏，在使用过程中复合材料层合板的性能优势得不到充分发挥[4]。纤维铺放技术的传统设计方法采用直线纤维制备材料层合板的铺放技术，受限于丝束铺设技术和设备的制约及优化时的计算消耗，大多采用0°、±45°、90°铺层方向，在承受面内压缩和剪切时，其稳定性无法满足要求。随着现代自动铺放制造技术的不断发展和成熟，为了满足更高的性能需求，采取纤维曲线铺放制备变刚度复合材料成了一个新的重要研究方向。

复合材料纤维曲线铺放技术的迅速发展，驱动了现代飞行器结构采用新铺设形式，实现更好的超轻、高强、高效结构性能。曲线纤维复合材料层合板的纤维铺设角可以连续变化[4]，剪裁设计空间大[5]、减重优势明显[6]。不断变化的纤维方向角使得每个铺层的刚度在不同位置各不相同，设计者可由此调整铺层的内在刚度分布，提高结构效率[7]。相比于传统直线纤维复合材料，曲线纤维复合材料具有如下突出优势：板厚度不变的情况下可以按需求改变其刚度分布[4-5]；仅通过改变纤维方向角就可以实现层合板在厚度上按设计需求连续变化[7-8]。为充分发挥复合材料纤维的承载性能，改变传统复合材料铺层结构和方式，采用纤维曲线铺放技术制备变刚度复合材料层合板，在降低制造成本和提高复合材料性能方面显示出了极为突出的优越性和极大的潜力[9]，将会成为未来高性能纤维复合材料发展的主流趋势之一，其突出的设计性和减重特点，也将使曲线纤维复合材料结构制备这一技术在飞行器结构的气动弹性剪裁设计中发挥更重要的作用[10]。

壁板局部屈曲问题是机翼结构设计中需要重点考虑的关键约束，而各向异性板的屈曲问题一直是学界的研究重点。Nardo[11]、Thielemann[12]和Green[13]较早对胶合板的屈曲问题进行了研究，并提出了傅里叶级数形式的封闭解。Ashton和Waddoups[14]将瑞利-里兹法应用于分析各向异性板的稳定性和动力学响应。瑞利-里兹法是求解正交各向异性材料即复合材料层合板时的常用半解析求解方法，许多学者应用基于正交多项式的瑞利-里兹法进行结构分析，发现正交多项式系较傅里叶级数或梁的模态函数有更好的收敛性。Loja 等[15]采用正交多项式，基于瑞利-里兹法分析层合板屈曲、自由振动和动力稳定性等问题。Wu 等[16-17]利用瑞利-里兹法对曲线纤维层合板的稳定性问题进行了研究，着重考虑了边界条件的引入和消去刚度的微分项，解决了变刚度层合板中Levy 型解析解难以求出的问题；还提出了一种改进的瑞利-里兹方法用于均匀轴压下的圆孔变角度纤维板的屈曲分析，证明了利用变刚度提高复合材料结构的抗屈曲性能是可行的。

国内也有多位学者和机构基于现有商业软件对纤维曲线铺设技术开展了相关研究。如秦永利等[18]对纤维曲线铺放的变刚度复合材料层合板的研究进展进行了具体的介绍，马永前等[19]用ABAQUS有限元软件对纤维曲线铺放的复合材料层合板进行了建模计算，验证其面内受力情况下，屈曲荷载显著提高，幅度达14%左右。杜宇等[20]通过复合材料层合板铺层角度的设计，使曲线纤维层合板的极限载荷和强度载荷较直线时提高30%。牛雪娟等[21]通过对变刚度铺放路径进行数学建模得到变刚度复合材料层合板的拓扑构型，利用有限元分析软件GENESIS 实现层合板拉伸分析。卫宇璇等[22]基于有限元软件对曲线纤维层合板进行了仿真模拟，研究了曲线纤维轨迹对复合材料层合板力学性能的影响。

综合来看，有限元法能够较好处理复杂的结构形式和边界条件，使研究对象从层合板拓展到复杂翼面结构，但有限元法的求解耗费大，单纯采用有限元模型会大幅增加结构优化的难度和计算耗费；解析法不能准确考虑气动弹性变形下的任意边界条件，无法适用于气动弹性优化。

为了解决有限元方法建模困难、求解速度慢，而解析法无法准确描述复杂边界条件的难题，本文通过在总势能方程中引入拉格朗日乘子的方式将复杂边界条件引入到壁板控制方程中，并通过Airy应力函数描述待求解的壁板内应力分布，以此建立了能考虑复杂边界条件的曲线纤维壁板力学模型；通过瑞利-里兹法进行解析求解，并采用勒让德多项式作为形函数以加快收敛速度、提高计算精度；采用牛顿-辛普森迭代方法进行后屈曲阶段的位移和应力求解，并使用自适应迭代步长来加快收敛速度。通过与有限元计算结果进行对比来验证该快速求解方法的准确性和精度，并比较二者在相同计算条件下的求解效率。最后基于该快速求解方法总结曲线纤维壁板在不同边界条件和设计构型下的屈曲/后屈曲力学特性。

1 基本理论与力学模型建立

1.1 曲线纤维描述方法

本文的参考纤维路径是通过沿特定方向和壁板的特定区域内线性改变纤维方向来定义的，如图1 所示；其余各纤维通过将该纤维沿一定方向平移得到。本文使用的命名法 ＆lt;θ1|θ2|θ3＆gt;表示单层的纤维变化，表示在壁板中设有3 个控制点，即在边界处有2 个控制点(点1 和点3)，在中心处有1 个控制点(点2)。纤维角度随位置变化形式可由式（1）描述。

图1 曲线纤维壁板纤维路径描述方法Fig.1 Description method of VAT fiber path

式中： θ(x) 为 坐标为x处 的纤维方向角；a为平板长度； θ1、 θ2和 θ3分别为3 个控制点处的纤维方向角。

本文曲线纤维设计采用2 种典型方法进行，即自动纤维 铺放技术(automatic fiberplacement,AFP)和连续纤维束剪切（continuous t ow shearing，CTS)法[23]。其中，AFP 方法不会改变纤维厚度，而采用CTS 方法进行设计时，由于该生产方式使得纤维束在层合板中以连续受力挤压的方式改变方向时保持单位长度的体积(即单位长度中能铺放纤维束的质量)恒定，因而纤维束的厚度增加、宽度减小，如图2 所示。采用CTS 方法进行曲线纤维设计时，纤维束的厚度分布可以采用恒定体积假设计算[23]：

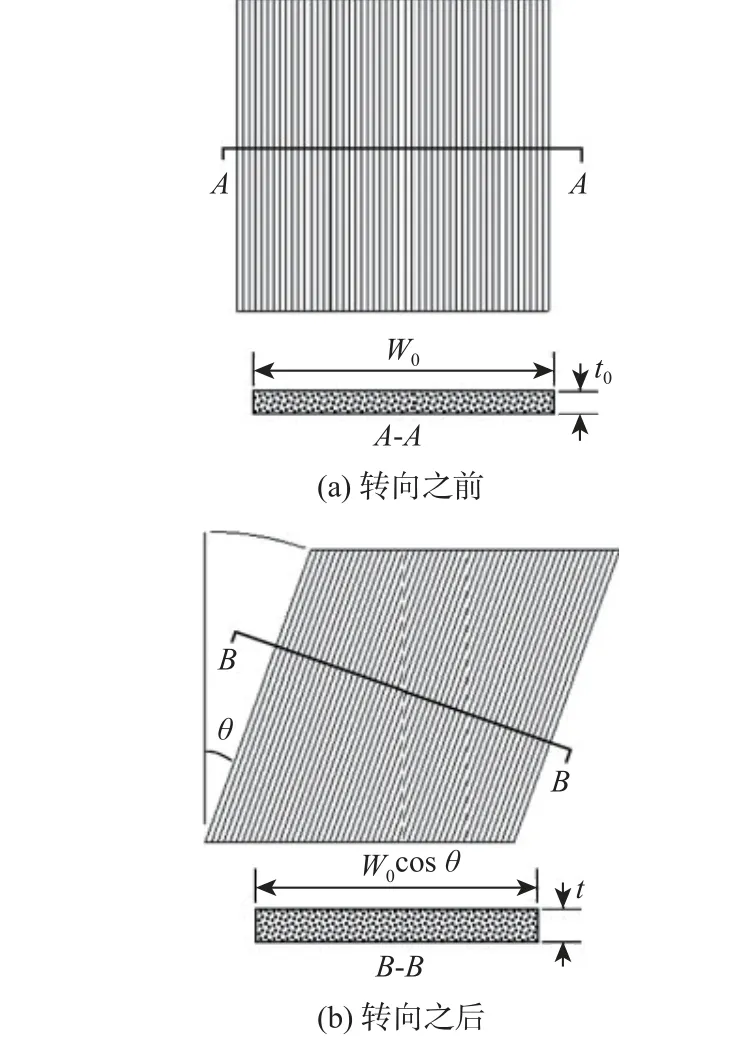
图2 丝束被剪切转向导致的厚度变化[23]Fig.2 Tow thickness variation by shearing [23]

式中：t为x处纤维束厚度；t0为参考点处的纤维束厚度； θ0为参考点处纤维方向角。

1.2 小变形分析基本理论

在前屈曲(pre-buckling)阶段，即载荷达到临界屈曲载荷之前，薄板处于小变形情况下，此时位移和应变是线性的；其中性面的横向正应力相比其他应力小得多，因而往往将其忽略。应变-位移关系也为线性，可表示为

式中：u、v、w分别为板各点在x、y、z这3 个方向的位移； εx、 εy和 εz为 对应方向的正应变； γ为切应变。式(3)中的应变分量在相容条件下变形可以得到：

式中：上标0 为在板的中性面处。

引入Airy 应力函数 Φ，其定义为

式中：Nx、Ny为壁板在x和y方向的合应力，即各层应力沿厚度积分后的结果；Nxy为切应力沿厚度积分结果。为简洁起见，本文部分式中的偏微分记号会以带逗号角标的形式出现，即w,x=∂w/∂x，可以将Airy 应力函数简写为

为进行屈曲分析，本文有如下假设：在屈曲出现之前，随着载荷的增加，薄板处于二维应力状态下，在本文记为[]，其中系数 λ是随着载荷增加而成比例单调增加的系数；应变增量与位移增量仍为线性关系，且应力增量依然遵循线性应力-应变关系，则面内的合应力增量与位移仍为如式(3)描述的线性关系。将式(3)～式(6)代入虚功原理表达式中，最终可得到各向同性薄板屈曲问题的最小势能原理表达式为

其中

式中： Πb为 势能的泛函；D为板的弯曲刚度；积分符号中的Sm为 板的积分区域； µ为泊松比。

1.3 曲线纤维层合板小变形分析方法

对直线纤维层合板，根据经典层合板理论得到本构方程[24]：

式中：A、B和D分别为复合材料板的面内、耦合和弯 曲 刚度矩阵； ε0为 中性面的应变； κ为 中 性 面 曲率；N和M分别为面内合应力和合弯矩。

而对于曲线纤维层合板，其A、B、D矩阵中各项不再是常数，而会随位置改变，此时式(8)可以写成如下形式[25]：

为便于后续计算，将式(9)改写成部分求逆形式[25]：

对于本文所研究的对称均衡铺层，弯曲-面内耦合矩阵B=0，从而B*=0，D*=D。

根据式(10)的本构方程，中性面的应变和合应力N之间的关系可以由如下方程得出：

式中：aij为 面内刚度矩阵A中各项对应数值。将相容方程式(4)和平衡方程式(11)代入应变能方程，并引入拉格朗日乘子描述的边界条件，可以得到曲线纤维壁板在小变形情况下由于面内拉伸/压缩所引起的总泛函方程：

式中：C1为 载荷边界；C2为位移约束边界；Mv0为中性面处外力矩；V z0为中性面处集中力；u0和v0分别为位移约束边界沿x和y方向的位移分布。式(12)中受变分影响的函数为待求的应力函数 Φ和边界应力，可通过瑞利-里兹法进行求解。同样可以得到曲线纤维薄板在小变形情况下由于弯曲引起的总泛函方程：

式中： λ为屈曲因子；等号右边第1 个积分项为板的弯曲所具有的应变能；等号右边第2 个积分项为相容方程和位移方程的耦合关系。式(13)中受变分影响的函数为位移函数w。

1.4 曲线纤维层合板大变形分析方法

在进行相应的分析和公式推导之前，本文对于大变形的定义如下：

1)变形足够大(即变形是板厚度的数倍)，但仍足够小到适用简单的形式分析板的曲度；

2)在弯曲时，中性面产生了应变。

此时任意一点处的应力-应变关系仍为线性，但位移-应变关系不再是线性，可通过微分形式的冯卡门大变形方程(von Kármánlargedef lection equations)作为控制方程给出[24]。忽略高阶项，板的中性面应变和中性面位移间的关系可以通过下式定义：

式中：e为非线性状态下的应变，以区分与线性状态下的应变ε。

需要注意的是，对于大变形下的屈曲问题，其非线性部分是由式(14)中非线性项的引入导致的，该部分非线性项导致了面内变形与弯曲变形的耦合，而这与材料属性(各向同性或各向异性；曲线纤维或直线纤维)均无关。但曲线纤维层合板由于其刚度特性随位置变化，会使得分析后的应力分布呈现更加非线性的形式。

当板处于大变形情况时，中性面产生了较大倾斜，此时的面内合应力Nx、Ny和Nxy会影响到z方向的平衡方程，曲线纤维壁板在大变形状态下的非线性平衡方程为[16,25]

同样地，可以得到曲线纤维板通过Airy 应力函数表示的非线性相容方程[16,25]：

进而可以建立曲线纤维壁板在大变形条件下，含有边界条件的总势能变分方程[16,25]：

式中：等号右边前2 项积分式为薄板的面内拉伸/压缩和弯曲引起的应变能；等号右边第3 项积分式为以应力函数 Φ的形式表示了相容方程和平衡方程之间的耦合关系；等号右边最后2 项积分式为一般边界条件；下标c1和c2分别为定义了应力和位移约束的边界。积分项s和v分别为沿给定边界的切线和法线方向。通过引入拉格朗日乘子，非线性的应变-位移关系能够被包含在势能方程式(17)中，从而不需要单独求解相容方程和平衡方程，这意味着仅需求解静止状态下的方程式(17)就能同时满足非线性平衡方程、相容方程、给定的弯矩及横向剪切合应力(面外)边界条件和位移(面内)边界条件。

2 瑞利-里兹求解方法

2.1 分析坐标系与形函数选择

本文将对y方向无约束(见图3(a))和y方向有位移约束(见图3(b))2 种不同的边界条件展开研究；如未加特殊说明，则表示纤维角度沿x方向改变，载荷也沿x方向施加于薄板上。为简单起见，将分析坐标系进行归一化：

图3 曲线纤维薄板载荷、位移及坐标系示意图Fig.3 Load, displacement and coordinate of VAT fiber plate

式中：a为平板长度；b为平板宽度。

本文采用瑞利-里兹模型进行屈曲、后屈曲分析，将位移函数w和Airy 应力函数 Φ假设为如下的级数形式[25]：

式中：Xm、Yn、Xp、Yq为满足给定边界条件的形函数；Φ0(ξ,η)为沿边界处的未知法向应力分布(Nx0,Ny0)。可以表示成如下形式以符合实际应力分布：

式中：cl和dl分别为应力函数对于给定边界条件的未知应力场的各阶形函数的待定系数。具体地，在薄板各方向边界处可以得到边界处应力与形函数之间的对应关系：

式中： φ (η)、 ψ (ξ)为应力的形函数。给定的位移载荷形式需要与待求的边界合应力分布结合，并将其代入式(12)的边界积分项中进行未知量( Φpq、cl、dl)的求解。

对于式(19)～式(22)中形函数的选择，需要考虑面内边界条件和对应的面内应力状态。对经典形函数的相关研究表明[17]，三角函数多项式由于具有周期性，适用于求解具有周期性的力学问题；勒让德函数具有非周期性，适用于非周期性问题的求解。对于本文所研究的稳定性问题，非周期的勒让德多项式作为形函数具有更好的收敛性和求解精度。为加快收敛速度，本文选择勒让德多项式作为形函数；为使其形式满足边界条件，需对勒让德多项式乘以( 1−ξ2)或 ( 1−η2)：

其中勒让德形函数Lr(ξ)一般形式为[17]

本文进行的数值实验结果如图4 所示，纵轴为计算值和有限元结果的比值；横轴坐标“x-y-z”中的数字含义如下：x、y分别对应表征结构刚度本身的形函数的阶数，而z对应边界处应力形函数阶数。前10 阶屈曲模态在选用5 阶形函数时即可实现收敛；对于第1 阶屈曲因子，只需表征结构刚度本身形函数的阶数(即x)达到7 阶、其余形函数仍为5 阶即可具有足够的精度，第1 阶屈曲因子相对误差为1.3%。该实验结果证明，勒让德多项式在分析板的屈曲问题时具有较好的收敛性和准确性。

图4 SSSS边界条件下不同形函数阶数屈曲因子计算结果对比Fig.4 Buckling factors comparison of different shape function orders under SSSS boundary condition

2.2 瑞利-里兹屈曲求解模型

小变形状态下式(12)和式(13)可以独立求解。将式(19)～式(22)代入式(12)，就可以得到以勒让德多项式作为形函数表示的面内拉伸/压缩对应边值问题的总泛函；其中需要进行求解的未知量共有3 组，分别是 Φpq、cl、dl。利用总泛函对未知量偏导数为0 的特性建立瑞利-里兹模型：

式中：fi分 别为 Φpq,cl,dl。

由式(25)可以得到一组线性代数方程，并可以表示为式(27)的张量形式，式(26)分别由式(12)对Φpq、cl和dl求偏导数得来：

式中：Kmc等项为板在小变形状态下的变分刚度矩阵，矩阵下标中的m、c、d 分别表示面内、x方向的边界(即边界a)和y方向的边界(即边界b)； Φ、c和d分别为未知量 Φpq、cl和dl的列向量形式；F x、F y分别为x方向和y方向的边界条件。式(27)可简写为式(28)，这与经典理论中的线性静力学问题具有相同表达形式：

对于图3（a）中y方向边界无约束时的边界条件(SSFF)，y方向无应力，直接得到dl=0，方程组退化为

由式(12)可得，对于坐标归一化后的薄板有：

注意到在本文所求解的壁板稳定性问题中，边界位移的分布形式u0(s)已知，且独立于应力分布，因此可得

由式(5)和式(22)可得

方程式(27)中并不包含位移函数w，仅能获取边界处的载荷和板的应力分布形式 Φ。为了获得板的屈曲因子及对应的屈曲模态信息，需要通过求解弯曲对应的总泛函方程式(13)获得。采用与式(25)相似的方法，可以得到由待求位移函数的系数W表示的给定合应力状态下的屈曲问题，并可改写成求解矩阵特征值的形式如下：

式中：矩阵下标中的b 表示弯曲； λ为对应刚度矩阵的特征值，按从小到大排序后即为各阶屈曲模态对应的屈曲因子；W为各阶屈曲模态的特征向量(即振型)。给定载荷F与屈曲临界载荷Fcr的关系为

2.3 大变形瑞利-里兹求解方法

与屈曲求解方法相似，将形函数表达式(19)～式(23)代入大变形总泛函方程式(17)，就可以得到以勒让德多项式作为形函数表示的对应边值问题的总泛函；其中需要同时进行求解的未知量共有4 组，分别是 Φpq、cl、dl和Wmn。同样利用总泛函对未知量偏导数为零的特性建立瑞利-里兹模型：

式中：fi分 别为 Φpq,cl,dl,Wmn。

由式(35)可以得到一组非线性代数方程，并可以表示为如式(36)的形式，分别由式(17)对 ϕpq、cl、dl和Wmn求偏导数得来：

式中：各矩阵的记号含义与式(27)和式(33)中相同；W为式(17)中形函数系数Wmn的列向量形式。实际上，所有涉及到2 个未知量的耦合矩阵(如Kbm、Kbc、Kbd)实际为3 阶张量，为了保持表达统一及便于理解，本文仍写作矩阵的形式，而在其具体表达形式中写成三维数组的形式。在计算时，涉及到此类数组的乘法运算时仅对后二维所构成的n个矩阵依次进行矩阵乘法，并将结果对应排列，则计算结果仍为列向量形式，具体过程不再赘述。

式(36)实际为式(27)和式(33)及额外的非线性耦合项组合得到，这些耦合项正来源于大变形状态下面内合应力对于中性面平衡方程的影响，即面内-弯曲耦合关系；该非线性方程无显式求解方法。在求解时，首先通过求解式(27)或式(29)得到前屈曲状态时的合应力分布形式(即变量 Φ、c和d)，并代入式(33)得到板的临界屈曲载荷Ncr和临界状态的位移函数(即W)；之后进行后屈曲求解，本文通过牛顿-辛普森迭代方法来求解非线性代数方程式(36)并获得后屈曲的平衡路径，即加载步长载荷与位移的关系。下面给出具体的迭代求解格式推导。非线性方程式(36)中的4 个方程可以写为

实际计算中，仅使用经典的牛顿-辛普森迭代法可能会在求解部分算例时出现数值不稳定，因此，需加入阻尼因子 α以增强稳定性：

式中： α一般取(0,1)之间的数值，越接近0 则阻尼越大， α=1则表示无阻尼。

非线性矩阵方程F(X) 对自变量X的导数即方程组(37)的雅可比矩阵J，其形式为

式中：3 阶张量的各耦合矩阵与向量相乘后退化为2 阶张量，即矩阵；进行此类运算时仅对三维数组中对应的某一维展开。

在进行求解时，先将给定的载荷分解成若干级微小载荷逐次加载，并在每个加载步中采用迭代法求解得到位移函数w和应力函数 Φ的待定系数，直至2 次迭代的残差 ε小于给定值(本文取10−4)后认为收敛并计算下一个加载步。该屈曲/后屈曲求解流程如图5 所示，其中残差 ε的计算形式为

图5 屈曲/后屈曲求解流程Fig.5 Analysis flow of buckling and post-buckling

3 有限元模型与求解策略

3.1 有限元求解模型

为验证本节所建立的曲线纤维壁板屈曲分析方法的正确性及其在机翼蒙皮局部壁板屈曲分析中的适用性，选取某大型商用客机机翼上翼面的部分蒙皮壁板作为研究对象，如图6(a)中红色部分所示。壁板在面内主要承受沿展向的压缩载荷，如图6(b)中的箭头所示，该壁板四周均为刚度较大的翼肋或翼梁，在机翼受到气动载荷而产生变形时，壁板上下边界受到翼肋沿展向的挤压而发生变形，而左右边界向外延展的趋势受到翼梁的限制，此时可认为该壁板具有位移约束的边界条件。且该壁板沿展向曲率为0，沿弦向的曲率很小，对其受到沿展向压缩时的稳定性影响有限，因此，可简化成矩形平板进行研究，其边界条件和分析坐标系如图6(b)所示，瑞利-里兹法求解通过MATLAB 自编程序实现。采用Patran 建立曲线纤维复合材料矩形层合板的有限元模型，如图6(c)所示，其中红色箭头表示对应单元内纤维方向；并采用Nastran 对其进行了屈曲分析。壁板的几何尺寸为 450 mm×750 mm，材料常数及铺层厚度如表1 所示。本文除分析图3 中所示的侧边自由(SSFF)和侧边施加位移约束(SSSS)这2 种不同情况外(其中a=450 mm，b=750 mm，所给定的单侧位移边界条件 ∆x=10−3mm)，还对机翼在气动弹性变形下的复杂边界条件进行屈曲/后屈曲分析，并对比3 种不同边界条件对屈曲特性的影响。

表1 壁板采用材料的材料属性Table 1 M aterial properties of com posite used in panel

图6 局部屈曲分析所选取的壁板示意图Fig.6 Panel description of local buckling analysis

3.2 机翼弹性变形下壁板面内位移提取方法

在实际飞行状态中，机翼由于气动力作用而产生弹性变形。从宏观角度观察，该弹性变形表现为向上弯曲的挠度和各剖面的扭转；对局部壁板而言，该壁板的局部分析坐标系发生了位移和旋转，且该位移远远大于其边界处在面内的位移分量，如图7 所示。其中，蓝色的点为机翼变形前该壁板边界上的点，为方便分析将壁板平移其形心与坐标原点重合；红色的点为机翼变形后该壁板边界上的点。将变形后壁板的形心平移到坐标原点便可以清晰地观察到壁板局部坐标系即壁板本身的旋转(见图7(b))。需计算变形后局部坐标系在原分析坐标系下的表示形式，进而得出变形后的壁板边界各点在对应的局部坐标系中的坐标。

图7 机翼气动弹性变形前后上翼面壁板边界结点位置对比示意图Fig.7 Comparation of node location on edges of focusing panel before and after aeroelastic deformation

坐标系的旋转和平移采用如下方式：

式中： α、 β 和 γ分别为局部坐标系3 个坐标轴对应的单位向量在全局分析坐标系中的表达式(列向量形式[)；]为边界处各点在全局坐标系中的坐标；为对应点在局部分析坐标系中的坐标。

首先需要获得气动弹性分析后各结点的位移，进而可得到边界各点变形后的坐标；分别对变形前和变形后2 组结点采用式(41)的方法转换为局部坐标系中的坐标，此时便可将变形前后的壁板置入同一坐标系中进行分析。边界各点的面内位移也能随之获得，如图8 所示；注意此位移仅为示意而非真实位移，由于边界面内位移相比板的尺寸小2～3 个数量级，图8 中绘制的红色位移示意为各点实际位移放大1 000 倍后的结果。在本文的分析中，主要考虑由于面内压缩/拉伸位移对稳定性的影响，忽略对屈曲影响相对较小的剪切位移。最终提取得到的该壁板受压缩边界和横侧边界的位移边界条件随位置变化情况如图9 所示。

图8 转换为局部坐标系后各结点位移示意图Fig.8 Diagram of displacement of each node after conversion to a local coordinate system

图9 受压和横侧边界的位移分布示意图Fig.9 Displacement distribution of loading edges and transverse edges

3.3 后屈曲特性有限元分析策略

本文的非线性有限元分析使用MSC.Nastran 的SOL400 模块完成。在进行几何非线性分析时，对于不同构型，采用固定步长加载的方式难以获取各构型下的准确临界屈曲载荷；为了更准确地获取不同曲线纤维路径壁板的力学特性，并尽可能减小有限元软件计算耗费，本文采用了自适应的变步长分段加载策略。在进行非线性分析前，首先使用线性求解方法得出当前构型的临界屈曲位移 ∆xcr及1 阶屈曲模态；而后基于此进行几何非线性分析，在不同阶段采用不同加载步长，如图10(a)所示，其中横坐标为单侧位移，纵坐标为壁板加载端约束力。

通过计算相邻2 个加载点的斜率即可得到当前状态下结构的等效刚度，如图10(b)所示(壁板铺层参数为进而准确获得结构发生屈曲的临界点。几何非线性分析表明，对于本文的碳纤维复合材料曲线纤维壁板，采用线性方法得到的屈曲临界变形壁板端面合力与非线性方法获得的实际合力一致，误差可忽略。而屈曲实际发生时所对应的位移略小于线性分析结果，大致为线性结果的97%～98%；达到屈曲载荷后，壁板面内承载能力迅速下降。这表明，进行飞行器结构的壁板设计时，采用线性分析方法及线性临界屈曲载荷作为壁板稳定性约束是合理的，但超出该临界屈曲载荷后线性方法不能得到准确结果。

图10 铺层曲线纤维壁板(SSFF)几何非线性屈曲分析结果Fig.10 Geometry nonlinear buckling results of VAT panel under SSFF boundary condition

通过改变壁板x、y方向单元划分密度，可研究有限元方法的计算耗费与网格规模间的关系，如图11 所示，其对应边界条件为SSSS 边界，铺层参数采用CTS 设计，计算环境为W indows10 系统、i5-7200UCPU(2.50GHz)、8GB 内存的个人计算机；其中端面载荷表示加载至2 倍屈曲临界位移时加载边界的合外力，Ry表示沿y方向划分的单元数量。从中可以看出，由于曲线纤维壁板中纤维角度随位置变化，非线性屈曲较难收敛；本文中曲线纤维的变化沿x方向，因此y方向单元密度对结果影响程度较低，当单元划分数量达到20 时继续加密对结果影响十分有限；而x方向单元直接影响壁板刚度变化情况，划分密度不足则会引起数值波动，单元划分数量在130 以上时可避免波动，后屈曲载荷分析结果接近收敛。

图11 端面载荷及计算耗时随网格规模变化示意图Fig.11 Edge end load and calculation cost changes as mesh density

本文建立的快速求解框架虽然也使用了迭代求解，但其是基于一个含有所有未知量的单独方程进行的，无需在2 个方程(即平衡方程和相容方程)之间进行相互迭代，因此能够快速进行非线性分析。上述计算实验表明，经典的MSC.Nastran 软件达到数值稳定需耗费约200 s，其他如ABAQUS等软件耗时大体相当；而本文建立的快速求解方法可于10 s 左右完成非线性分析，求解速度远快于经典有限元软件，适用于非线性屈曲的大规模优化。

3.4 有限元与瑞利-里兹法对比验证

3.4.1 第1 阶模态屈曲因子对比

按3.2 节中描述的方法提取壁板受压和横侧边界的位移，分别采用有限元软件Nastran 和瑞利-里兹法进行屈曲分析。由于机翼整体的弯扭耦合效应等影响，边界上的位移值并非均布匀或线性变化，而呈现出较为复杂的分布形式。此时应力分布相比均布位移边界条件变化较大，应选取前n阶勒让德多项式以获得更好的收敛性。当壁板边界条件为均布位移约束的SSFF 或SSSS 边界条件时，对于直线纤维壁板、AFP 固定厚度设计及CTS 变厚度设计的曲线纤维壁板，瑞利-里兹法与Nastran 第1阶模态相对误差均小于0.5%，前5 阶模态相对误差小于1%。前5 阶模态振型均与Nastran 结果一致，为简略未进行展示。

为总结壁板屈曲特性随纤维角度变化的规律，以壁板双侧承载边界处控制点纤维角度设置为T1，壁板中心点处纤维角度为T2， 进行对称均衡纤维路径设计，即将壁板纤维路径设置为的对称均衡铺层形式；采用CTS 设计时，参考角度为边界处的控制点角度T1。分别固定其中一控制点角度为0°，计算第1 阶模态屈曲因子随另一控制点角度变化趋势，并与有限元结果进行对比，如图12 所示。

图12 固定一控制点角度、屈曲因子随另一控制点角度变化趋势Fig.12 Buckling factor variation along with angle of one control point (with the other point fixed)

从分析结果中可以看出壁板中心处纤维角度与边界处纤维角度对屈曲性能影响的差别。通过增加边界处的纤维角度能够取得更好的屈曲性能，尤其是采用CTS 变厚度设计时。在此非均布位移载荷作用下，瑞利-里兹法与有限元方法的分析精度相当，相对误差小于0.5%。

3.4.2 屈曲/后屈曲特性对比

通过本文建立的瑞利-里兹求解方法与有限元软件MSC.Nastran 对壁板在不同边界条件下的屈曲/后屈曲特性进行对比，验证2 种不同分析方法的准确性，及对不同边界条件的适用性，如图13 所示。其中，图13(a)和图13(b)的横坐标为加载边界的单侧边界位移量；图13(c)的横坐标为受压边界上一点的位移量，其余各点压缩/拉伸的位移量按照图9中的位移分布形式相应变化。从中可以明显看出，对于相同位移条件，采用CTS 设计可以有效增加临界载荷，但在后屈曲阶段承载效率与AFP 设计相当。2 种方法结果一致，验证了解析法和有限元方法进行后屈曲求解的准确性。

图13 不同边界条件曲线纤维壁板屈曲/后屈曲特性对比Fig.13 Buckling and post-buckling performance of VAT panel under different boundary conditions

4 曲线纤维壁板稳定性特性分析

为进一步分析曲线纤维壁板的屈曲/后屈曲特性，并更清晰地展示曲线纤维壁板稳定性随纤维路径参数变化的规律，采用瑞利-里兹法对纤维路径为的壁板进行稳定性分析，根据分析结果绘制相应的载荷-位移曲线。

对边界条件为SSSS 的曲线纤维壁板，分别固定一个控制点的纤维方向角，将另一控制点纤维方向角从0°变化至90°(变化间隔为10°)，其屈曲/后屈曲特性如图14 所示；其中圆圈处表示该构型的屈曲临界位移和载荷。其载荷-位移曲线随着一个控制点纤维方向角增大呈现出明显规律，即临界屈曲位移增加、斜率变小，如图14(a)所示。

图14 SSSS边界条件的曲线纤维壁板屈曲/后屈曲特性Fig.14 Buckling and post-buckling performance of VAT panel under SSSS boundary condition

可以发现，虽然增加控制点的纤维方向角能够增加其临界屈曲位移，但对应载荷并非持续增加；且当固定壁板边界处控制点T1=30◦时，屈曲载荷随着中心处控制点T2的角度增加而先减小后增加；反之，当固定T2=30◦时 ，壁板屈曲载荷随T1的角度先增加后减小。为更清晰展示这一规律，将各组控制点参数组合的临界屈曲载荷在同一坐标系中绘制，如图15 所示。

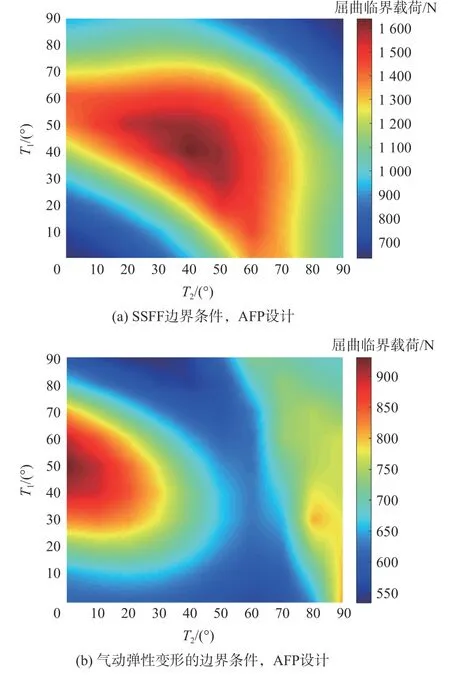
图15 不同边界条件的屈曲临界载荷Fig.15 Critical load of VAT panel under different boundary conditions

从图15 中可以观察到，当采用固定厚度的AFP设计时，对于SSFF 边界条件(见图15(a))的壁板，其最大屈曲临界载荷出现在铺层形式为 ±45◦的对称均衡铺层附近，与一般经验相符合；对采用SSSS 边界条件或基于气弹变形边界条件(见图15(b))的壁板，采用的纤维路径能够使壁板获得最大屈曲载荷，采用不同角度的直线纤维可得到的屈曲载荷则落在T1=T2的直线上，经比较发现，曲线纤维最大屈曲载荷约为直线纤维最大屈曲载荷的1.28 倍。采用变厚度的CTS 设计时，3 种不同边界条件的临界屈曲载荷均有大幅度提升，且分布形式十分接近。

为进一步比较屈曲前后壁板等效刚度变化，选取屈曲临界点的载荷随位移变化的斜率作为屈曲前等效刚度，选取 ∆x=2∆xcr即2 倍临界位移点与屈曲临界点连线的斜率作为屈曲后等效刚度；壁板等效刚度随控制点参数变化的规律如图16 所示。

图16 屈曲前等效刚度分布示意图(SSSS/AFP设计)Fig.16 Distribution of equivalented stiffness before and afterbuckling(SSSS/AFP design)

壁板在3 种不同条件下屈曲前等效刚度随控制点变化趋势基本一致；采用CTS 设计时，虽能有效提高屈曲载荷，但其等效刚度并未有明显变化。对SSSS 边界条件和基于气动弹性位移的边界条件，屈曲前后等效刚度分布形式接近，但其具体数值有大幅度下降。

为进一步比较壁板在后屈曲时出现的刚度下降，将组控制点参数对应的屈曲后等效刚度与屈曲前等效刚度做商，即可得到该曲线纤维路径下屈曲后刚度下降的百分比，如图17 所示。

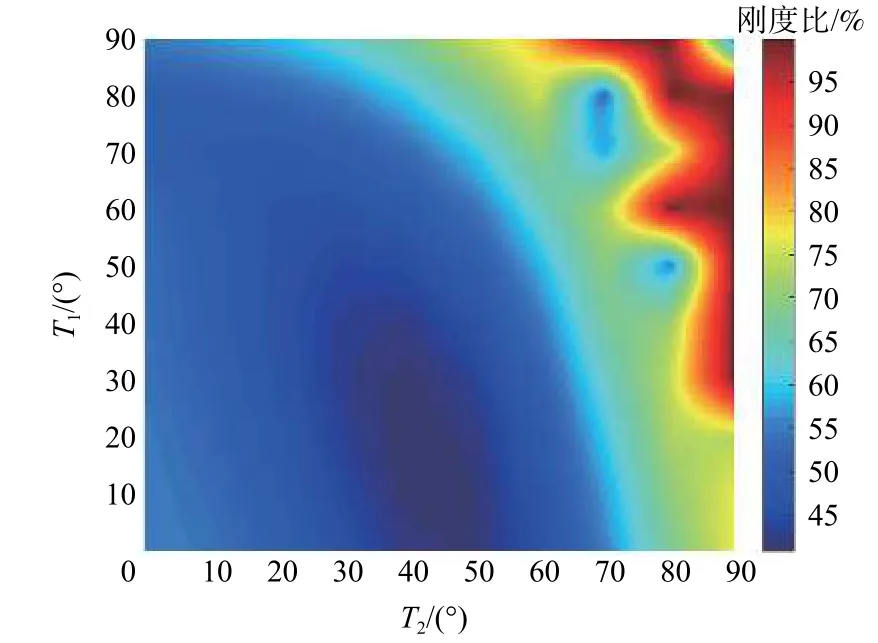
图17 SSSS边界条件、CTS设计壁板屈曲后刚度比Fig.17 Proportion of equivalented stiffness after buckling compared with stiffness before buckling

从图17 中可以看出，虽然纤维方向角度较小时其等效刚度较大，但在后屈曲阶段下降的幅度也更大，即面内稳定性较差；相反，纤维角度较大时，其等效刚度较小，但在后屈曲阶段的等效刚度损失更小，部分参数甚至无刚度损失。总体而言，曲线纤维由于具有更大的设计空间和更强的载荷重新分配能力，其临界屈曲载荷更高，能够提供更高的结构效率和面内稳定性。

5 结 论

本文基于冯卡门大变形方程，发展了能考虑任意边界条件的曲线纤维壁板屈曲/后屈曲特性快速求解方法，得出以下结论：

1）本文发展的瑞利-里兹求解方法适用于曲线纤维壁板的屈曲/后屈曲分析，线性阶段和几何非线性大变形下力学特性分析精度与有限元方法一致，且求解速度大大高于有限元软件。

2）曲线纤维复合材料具有更大的设计空间和载荷重新分配能力，在SSSS 边界条件或提取的气动弹性位移边界条件下、几何尺寸在m 量级、厚度在mm 量级的壁板，其曲线纤维设计得到的最大屈曲载荷约为同厚度直线纤维最大屈曲载荷的1.28 倍。

3）在后屈曲阶段，壁板承载能力(即等效刚度)随纤维角度不同而具有不同下降趋势；纤维角度较小时该下降更为明显。

4）本文的快速分析方法适用于在设计初步阶段快速掌握曲线纤维壁板面内稳定性的规律或大规模优化。