基于组合优化算法的空面导弹全空域弹道优化
祝雯生,吕先敬,侯振乾,张顺家,毕鹏,仲康
(1.上海机电工程研究所,上海 201109;2.空军装备部驻上海地区军事代表局,上海 200030)
在现代高动态攻防对抗中,导弹以最快时间到达目标,对作战效能有着极大的影响,如何在对飞行弹道最大高度、攻角、动压、末速等多项约束下实现最快时间到达目标,是弹道设计的工作重点[1]。随着载机性能的不断提升,其飞行包线范围越来越大,导致其挂载导弹的发射条件越来越复杂[2]。而弹道制导律中各个参数都会受到发射条件的影响,制导律需要在全空域内自适应变化,实现导弹全空域最快时间到达。因此,需要开展全空域弹道优化工作。
全空域是指根据导弹战技指标、发射条件、目标类型、作战场景等要素所确定的导弹飞行空域。全空域弹道优化是指在给定导弹气动参数、推进系统参数、全弹质量特性的前提下,通过优化制导律参数,在多种约束条件下实现全空域任意发射条件下导弹飞行弹道的性能最优。由于需要对全空域下的各个发射条件进行弹道优化,优化工作量巨大。为此,需要构建全空域弹道制导律代理模型,在此基础上开展科学、合理的弹道优化工作。代理模型技术可以通过少量的样本点即可较为精确地预估其他样本点的响应值,从而大幅度提高优化的效率,显著减少计算量[3]。
国内外对弹道优化问题已有诸多研究,汤祁忠等[4]基于简化的纵向平面弹道模型,在经典遗传算法的基础上,采用直接单重打靶法离散化控制变量,设计了末端多约束弹道的优化方法。李怡昕等[5]采用高斯伪谱法对变推力导弹的弹道进行优化,其仿真结果表明高斯伪谱法应用于可变推力导弹弹道优化设计的有效性。李伟喆和陈万春[6]分别以飞行时间最短和末速最大为优化目标,采用hp自适应Radau 伪谱法求解双脉冲中程空空导弹多段多约束的弹道优化问题,并根据求解结果分析了不同飞行条件对导弹性能的影响。韩聪聪等[7]采用基于单纯形-遗传算法,以二级弹道导弹为例,建立导弹主动段的弹道射程优化模型。优化结果表明:此复合优化算法在弹道优化应用中是可行有效的,并具有精度高、收敛速度快的特点。文献[4-7]弹道优化工作方面取得了许多研究成果,然而对全空域范围的弹道优化问题缺乏相关研究。
本文以空面导弹为对象,研究其在全空域范围内的弹道优化问题,采用组合优化算法,以平均速度为优化目标,考虑高度、攻角、动压、末速等多项约束条件,对空面导弹的飞行弹道进行优化,为全空域制导律设计提供支撑。
1 弹道优化模型
1.1 弹道模型
空面导弹的弹道模型通过求解三自由度质点弹道方程完成,根据设定的导弹和目标信息(发射条件)计算导弹的质心运动规律,其计算过程包括:弹目相对运动解算、确定标准大气参数、制导律和平衡方程计算、气动力和推力计算、质量质心计算、导弹运动参数和目标运动参数更新。计算时首先迭代求解平衡方程,获得导弹飞行所需的平衡攻角及平衡舵偏角,由此计算出作用于导弹的气动力,同时计算出当前的推力和质量,进而积分求解出导弹弹体动力学方程,最终给出随时间变化的导弹质心运动规律[8]。
空面导弹在三维空间中攻击目标过程中,导弹和目标的相对运动关系如图1 所示。图1 中Oxyz为惯性坐标系;M、T分别为导弹和目标(均视为质点);r为导弹与目标之间的相对距离;qε、qβ分别为弹目视线高低角和方位角;vm、vt分别为导弹和目标的速度;θm、φm分别为导弹的弹道倾角和弹道偏角;θt、φt分别为目标的弹道倾角和弹道偏角。
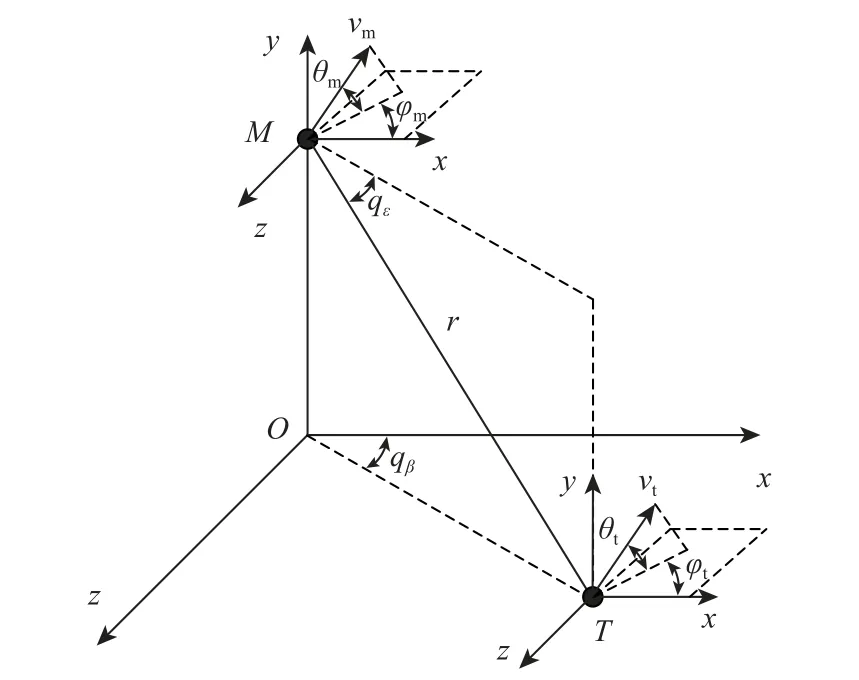
图1 弹目相对运动示意图Fig.1 Schematic diagram of relative motion between missile and target
根据图1 所示的导弹与目标之间相对运动关系,可以建立三维空间下导弹-目标的相对运动方程[9]:
导弹的动力学方程为
式中:ax、ay和az分别为导弹加速度在x、y、z这3 个方向上的分量。
导弹的运动方程[10]可由导弹速度vm在惯性坐标系Oxyz的3 个坐标轴分解得到,可表示为
式中:x˙m、y˙m、z˙m为导弹质心在惯性坐标系下的三轴速度。
同理,目标运动方程也可由目标速度vt在惯性坐标系Oxyz的3 个坐标轴分解得到。
1.2 优化控制变量
空面导弹的典型飞行过程可分为3 个阶段:初制导段、中制导段和末制导段[11],如图2 所示。初制导段以初始高抛角射入较高的空域,形成利于中制导段的飞行态势;中制导段继续以高抛态势飞行,快速进入高空,低大气密度能够减少气动阻力,提高导弹射程和末速;末制导段导引头截获目标,导弹以指定角度(落角)攻击目标,以保证对目标的打击精度[12-14]。因此,初制导高抛角和落角的选择很大程度决定了导弹的飞行弹道。为此,本文选择高抛角θΔ和落角θf为优化控制变量。

图2 空面导弹典型飞行过程Fig.2 Typical flight process of air-to-surface missile
1.3 性能指标
平均速度是空面导弹关键的性能指标。平均速度快,飞行时间短,不仅可以为载机尽快脱离战场提供条件,还可以降低导弹惯性组件的积累误差。本文以平均速度最大为优化目标,在全空域范围内对空面导弹的弹道进行优化设计。
目标函数选择为
式中:Vaverage为导弹的平均速度。
1.4 约束条件
本文主要考虑以下5 种约束条件:
1)高度约束。高空大气密度低,如在4 5 km 高度处大气密度仅为海平面的0.16%,因此,空面导弹通常会飞行到高空以减小气动阻力。但如果导弹飞行高度过高,其飞行路径将随之增长,由于受到发动机总能量限制,速度并不会无限增加,存在上限,此时过长的飞行路径反而会降低平均速度。因此,需要设置高度约束,即
式中:Hmax为导弹最大飞行高度。
2)攻角约束。在飞行过程中,为减少导弹能量的损耗,保证整个飞行过程状态稳定,必须约束攻角的范围,即
式中:αmax和αmin分别为导弹飞行过程中最大攻角和最小攻角。
3)末速约束。为了保证导弹在末制导段有足够的能量完成对目标的有效攻击,需要设置末速约束,即
式中:Vend为导弹的末速约束值。
4)动压约束。为保证导弹的飞行品质和可控性并满足结构强度要求,要求动压在一定范围内。因此给定动压约束,即
式中:qmax和qmin分别为导弹飞行过程中的最大动压和最小动压
5)舵偏角约束。为了保证导弹飞行姿态的稳定,舵偏角的大小通常是有限的,因此给定舵偏角约束,即
式中:δmax和δmin分别为导弹的最大舵偏角和最小舵偏角。
2 弹道优化方案设计
在全空域范围内进行弹道优化,需要将空域划分成若干个典型点,随后对其中每个典型点进行优化,这就导致计算量异常庞大。为此,需要构建全空域的代理模型,通过较少的样本点较为精确地预估其他样本点的响应值,随后对单个样本点进行优化,可以提升弹道优化的效率[15]。
本文建立全空域弹道2 级优化框架,如图3 所示,其基本思想是:①将优化流程分为2 个层次,即代理模型构建和子系统弹道优化;②把全空域范围内的导弹发射条件作为全局设计变量,全空域弹道代理模型的任务是构建导弹发射条件和优化控制变量(高抛角和落角)之间的关系;③子系统弹道优化的任务是在给定发射条件下,调整局部设计变量,在满足约束条件下,使弹道优化的目标最优。

图3 全空域弹道2级优化框架Fig.3 Two-level optimization framework for trajectory optimization in full airspace
2.1 代理模型
常用的代理模型有多种,如多项式响应面模型、径向基神经网络模型、K riging 模型和深度学习神经网络模型等,本文采用多项式响应面模型。采用响应面模型可以构造简单的代数表达式(多项式),考虑到空面导弹弹上计算机计算能力有限,多项式计算简单,可满足弹上计算机工程应用。
由于响应面模型在局部范围内比较精确的逼近函数关系,本文将空域按照高度进行划分,对各个高度的空域构建响应面模型,以提高代理模型的精度。代理模型的精度通常用复相关系数(R2)和均方根误差(root meansquare error,RMSE)来衡量。其中,R2用来衡量代理模型与样本点的近似程度,一般认为R2>0.9时,近似模型的精度可以接受;RMSE 用来衡量样本的离散程度,一般认为小于0.2 即满足要求[3]。
2.2 组合优化算法
目前,用于优化分析的优化算法通常可分为直接搜索算法、梯度优化算法和全局优化算法三类算法。直接搜索算法无需梯度信息,但有可能落入局部最优解;梯度优化算法优化效率高,但非常依赖初始设计点;全局优化算法搜索效率低,但能够有效搜索全局最优解。
本文空面导弹的全空域弹道优化问题是一种具有多种约束条件的非线性优化问题,采用直接搜索算法、梯度优化算法容易陷入局部极值状态,不能或不一定找到真正的最优解。目前的研究更倾向采用全局优化算法求解弹道优化问题,其对一些大型复杂非线性优化问题表现出良好的性能,缺点就是局部搜索效率低,最终的求解精度较差。
为此,本文提出一种基于多岛遗传算法[16](multi-island geneticalgorithm,M IGA)和序列二次规划法[17](sequential quadraticprogramming,SQP)的组合优化算法,所提算法结合全局优化算法和梯度优化算法的优点,具有鲁棒性强、高效、可靠、对初值不敏感等优点,可以保证全空域各个发射条件下的弹道优化都可以得到满意的最优解。
1)M IGA 优化算法。M IGA 优化算法是一种对传统遗传算法的改进算法,其将传统遗传算法的种群进一步划分为若干子群(岛),如图4 所示,在每个岛上运用传统遗传算法(genetic algorithm,GA)进行子种群进化(选择、交叉、变异等遗传操作),并每隔一定的代数进行岛间迁移,以维持种群的多样性,避免提前收敛。M IGA 具有比传统遗传算法更优良的全局求解能力和计算效率,在处理大规模复杂问题时具有较大的优势。

图4 传统GA和MIGA对比Fig.4 Comparison between traditional GA and MIGA
M IGA 的基本步骤为:①生成初始种群;②计算每一个个体的适应度;③按照精英保留策略选择将要进入下一代的个体;④对种群进行选择、交叉和变异运算,形成新的种群,并且每隔几代挑选子群中的个体进行迁移操作;⑤新种群作为初始种群,重复第2~4 步直至满足迭代停止条件。
2)SQP 优化算法。SQP 优化算法的核心思想是在每个迭代点x k构造一个二次规划问题,以其解作为迭代搜索方向,并沿该方向进行一维搜索得到新的迭代点,通过反复迭代最终逼近约束优化问题的最优解。二次规划子问题描述如下:
式中:H k为Hessian 矩阵的正定近似矩阵;hi(x k)和gj(x k)分别为等式约束和不等式约束函数;f(x k)为目标函数;d为搜索方向向量。
解式(10)得出当前迭代下搜索方向d k,从而得出新的迭代点:
式中:αk为步长参数。
随后利用新的迭代点x k+1对H k进行更新:
式 中:s k=x k+1−x k;y k=G k+1−G k,G k为Lagrange 函数的一阶导数。
3)M IGA-SQP 组 合 优 化 算 法。M IGA-SQP 组合优化算法的核心思想为:①采用M IGA 进行初步优化,得到精度较差但全局收敛性较好的次优解;②采用SQP 在搜索到的次优解附近进行局部精确搜索,以确保解的最优性。M IGA-SQP 组合优化算法兼具两算法的优点,通过M IGA 确保可以找到一个全局性较好的优化解,避免陷入局部最优解的困境,同时又通过SQP 来弥补M IGA 的缺点,从而提高搜索速度和优化精度。
2.3 弹道优化流程
空面导弹全空域弹道优化流程如图5 所示。

图5 全空域弹道优化流程Fig.5 Flowchart of trajectory optimization in full airspace
1)在全空域范围内,对发射条件(发射速度、发射高度、弹目距离等)构建样本点,通过M IGA-SQP组合优化算法对每个样本点进行优化。
2)根据弹道优化模型,确定初始种群和目标函数,通过M IGA 进行遗传进化产生新一代种群,选择其中优异的个体更新种群,经过多代遗传得到具有较好全局收敛性的次优解。
3)以次优解作为SQP 算法的初值,植入SQP算法深度寻优,通过弹道计算得到弹道性能指标,随后判断结果能否达到要求的精度,若满足则得到当前样本点的最优解,若不满足则重新进行SQP 优化迭代。
4)基于所有样本点的优化结果,采用三阶多项式响应面方法构造全空域弹道代理模型,建立全空域发射条件相对优化控制变量之间的拟合函数关系式。当发射条件改变后,全空域弹道代理模型给出此发射条件下的高抛角和落角。
3 算例分析
根据空面导弹全空域弹道优化流程(见图5),进行全空域弹道优化。全空域发射条件的范围如下:
式中:Hm0、Mam0分别为导弹发射高度和马赫数;xt0、yt0分别为导弹发射时刻目标的x向和y向位置坐标。
为了得到具有工程意义的解,给出优化控制变量和约束条件的范围如下:
在优化求解过程中,M IGA 算法取子种群规模选择5,岛的个数为4,总进化代数设为10,总迭代次数为200,交叉概率取0.8,变异概率取0.05,岛间迁移率取0.05;SQP 算法取迭代次数为50,相对步长为0.01,收敛精度为0.001。
为了便于分析全空域范围内弹道优化的结果,选取2 种典型发射条件的优化结果进行分析,如表1所示。为了体现所提组合算法的先进性和优势,本文将2 种发射条件下,采用M IGA、SQP 和M IGA-SQP这3 种优化算法得到的迭代收敛情况进行对比分析,如图6 所示。其中,矩形曲线为采用M IGA-SQP算法得到的收敛曲线,黑色矩形为M IGA 算法中每一代的最优值(共10 代),红色矩形为SQP 算法得到的优化结果;圆点曲线为单独采用M IGA 算法得到的收敛曲线,黑色圆点为M IGA 算法中每一代的最优值(共20 代);三角曲线为单独采用SQP 算法得到的收敛曲线。
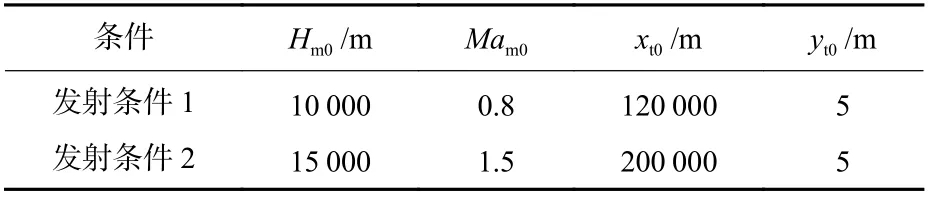
表1 典型发射条件Table 1 Typical launch conditions
从图6 中可以看出,单独采用M IGA 算法可以得到精度较差但全局收敛性较好的解,缺点是需要多代优化才能得到满意解(本文将代数设为20,总迭代次数为1 000);单独采用SQP 算法优化效率很高,但跟初值的选择关系较大,常常陷入局部最优;采用M IGA-SQP 算法可以有效地提高收敛精度和收敛速度,具有很好的收敛性。

图6 平均速度迭代收敛结果Fig.6 Iteration convergence results history of average velocity
如图7 和图8 所示2 种发射条件下优化前后弹道和速度对比曲线。从图7 和图8 中可以看出,优化后的高抛角和落角使得弹道的中制导段速度更快,速度分布更为合理,能量利用率更高。

图7 2种发射条件下优化前后弹道曲线Fig.7 Trajectory before and after optimization under two launch conditions
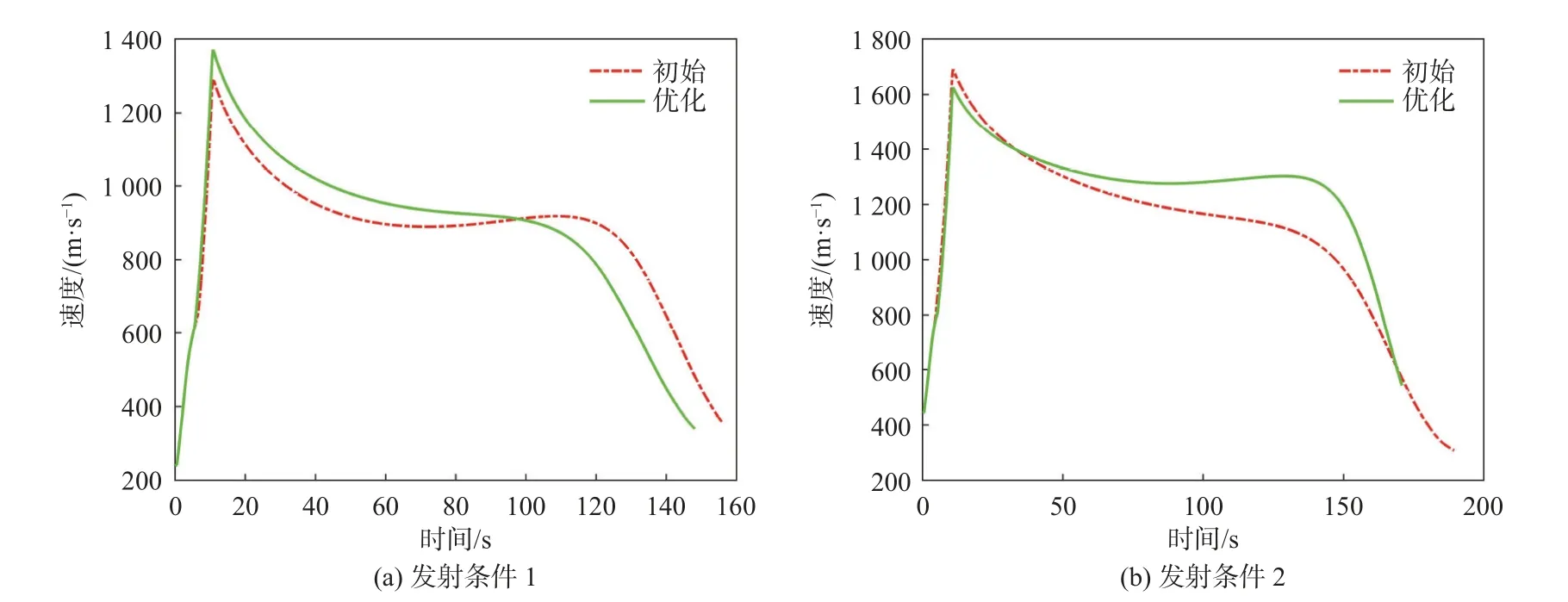
图8 2种发射条件下优化前后速度曲线Fig.8 Velocity curve before and after optimization under two launch conditions
表2 给出了2 种发射条件下弹道优化前后各个阶段的平均速度对比。从表2 中可以发现,整个弹道优化对初制导平均速度的提升有限,因为初制导时间较短;优化主要用于提高中制导段的平均速度,此段飞行距离最远,耗时最长,对整条弹道的影响也最大;当中制导段的平均速度提升后,给末制导段留下更多能量,末制导段平均速度随之提高。弹道优化通过优化出合理的高抛角和落角,使得中制导段的能量和速度损失最低,从而提高整个弹道的平均速度。

表2 优化前后各个阶段的平均速度对比Table 2 Comparison of average velocity for each stage before and after optim ization
在全空域范围内构建发射条件对高抛角和落角的代理模型,并通过三阶多项式函数表达,如式(15)所示。随后,对代理模型进行误差分析,其结果如表3 所示。其中,各个发射高度下高抛角和落角的R2基本大于0.9,RMSE 的值均较小,代理模型的精度较高,满足工程要求。

表3 代理模型误差分析Table 3 Error analysis for surrogate m odel
4 结 论
1)本文针对空面导弹全空域弹道优化问题,建立了多约束的弹道优化模型,并提出一种基于M IGA和SQP 的组合优化算法,采用M IGA 算法进行全局搜索优化,随后采用SQP 算法在全局优化结果的附近进行局部寻优。算例结果表明,M IGA-SQP 组合算法有效地结合了2 种算法的优势,克服了M IGA无法得到精确的全局最优值和SQP 对初值要求高的缺陷,算法精度相对较高,收敛速度较快,可以有效解决全空域弹道优化计算量大的问题。
2)采用多项式响应面代理模型技术,建立了全空域下的发射条件相对高抛角和落角的拟合函数关系式,为全空域制导律设计提供有力的支撑。算例结果表明,多项式响应面代理模型具有较高的精度,可以极大降低全空域弹道优化的计算量。
本文在全空域弹道优化过程中未将发动机参数(推力、工作时间等)考虑进去,在今后研究中,还需进行发动机与导弹总体的综合优化设计,以实现导弹总体性能最优。

