非线性能量阱在大跨度桥梁涡致振动控制中的应用

摘要：文章对非线性能量阱在大跨度桥梁涡致振动控制中的应用进行研究，将桥梁涡振激励等效为简谐荷载，建立涡激力下桥梁结构-NES动力学模型，基于数值搜索方法，给出NES参数设置及优化策略，并以国内某大跨度钢箱梁悬索桥为例，对NES的涡振控制性能进行数值模拟分析。结果表明，NES能有效抑制桥梁结构涡振响应幅值，其较无控制时降低了约84%。研究结果可为相关工程建设提供一定的理论和实践指导，对于解决桥梁涡致振动问题具有重要意义。

关键词：非线性能量阱；大跨度桥梁；涡激共振；结构振动控制；非线性振动

0引言

近年来，随着现代交通事业的飞速发展，特大型桥梁建设的规模和数量也在不断扩大。大跨度的桥梁在为人们出行带来了更多便利的同时，也使桥梁结构在风荷载作用下所产生的动力响应越发明显，涡激振动便是大跨度桥梁常遇见的问题之一。桥梁涡振是一种限幅振动，尽管其很少造成桥梁结构性破坏，但会影响行车体验感、舒适性，易诱发交通安全事故。因此，如何采取有效的措施减缓或消除桥梁涡致振动现象日益成为研究者们关注的焦点［1］。

调谐质量阻尼器（Tuned Mass Damper，TMD）是一种被动控制技术，因其具备安全可靠、经济实用、易于施工等特点，在桥梁工程风振控制中得到广泛应用。例如，日本东京湾航道桥、中国崇启长江公路大桥和西堠门大桥等都使用了TMD技术对桥梁涡振进行控制，工程实践结果表明其能有效地降低桥梁结构的风振响应，提高桥梁的安全性能［2-3］。然而TMD技术也存在许多问题，如对主体结构动力特性变化敏感、作用频段单一等，这极大地阻碍了TMD的发展。

近年来，随着非线性动力学理论的不断丰富与发展，具有非线性特性的质量阻尼器——非线性能量阱（Nonlinear Energy Sink，NES）已成为一种新型的振动控制手段，其相较于传统TMD装置，具有更宽的减振频带及更强的鲁棒性，在许多领域得到了广泛研究［4-6］。其中，部分学者将NES应用到了桥梁结构振动控制领域的研究中，取得了一系列进展。杨兴森等［7］以铁路简支梁桥为例，开展了基于NES的桥梁振动能量采集装置的适用性研究，结果发现基于NES的能量采集装置，具有减振频带宽、能量采集高效等特点，能有效抑制随机振动激励下的桥梁结构振动响应。Younesian等［8］针对铁路桥在周期性列车荷载作用下，产生过大振幅进而导致铁路桥发生疲劳破坏的问题，发现通过合理设计NES能抑制移动荷载下铁路桥梁的振动响应，使桥梁挠度降低＞43%。此外，对于大跨度桥梁而言，当其所受风荷载超过某一临界值时，可能会发生气动弹性失稳现象，导致桥梁结构的安全性受到威胁。为此，Vaurigaud等［9］通过在大跨桥上附加三次刚度NES来抑制大跨桥在耦合颤振下的气动弹性失稳，研究结果表明，NES与桥梁间能实现靶向能量传递，进而有效地控制大跨桥梁的气动弹性失稳，提高结构的安全性能。

由上述研究可知，相比于传统的线性振动控制方法，非线性能量阱具有更高的减振效果和更强的适应性，但目前非线性能量阱在桥梁涡致振动控制方面的研究尚不多见。基于此，本文开展了NES在大跨度桥梁涡致振动控制中的应用研究，运用结构动力学模态分析理论，建立涡激力作用下桥梁结构-NES系统非线性动力学方程，给出NES参数设置及优化策略，并以国内某大跨度钢箱梁悬索桥为例，对NES的涡振控制性能进行分析，探究其实际减振控制效果，为NES在桥梁抗风中的设计应用提供一定的理论和实践指导。

1 动力模型的建立

1.1 NES装置及其减振机理

NES本质是由一个质量块通过强非线性弹簧元件及阻尼元件与主结构相连接构成。由于其恢復力是由强非线性刚度元件提供的，这使NES具有不恒定的刚度，能够与极其广泛的频率发生共振，具有优越的频率鲁棒性。同时，NES适用于不同的激励条件，并且对于结构类型及结构的自身特性变化不敏感，克服了传统TMD装置鲁棒性低、作用频段窄的问题，在各领域都有很好的应用前景。NES与线性TMD调谐减振机制不同，其主要是通过瞬时共振捕获实现靶向能量传递（Target Energy Transfe，TET），以及利用强调制和混沌等非线性响应机制，实现对主结构能量的高效抑制和吸收。本文采用应用广泛的3次非线性刚度NES，对其在桥梁结构风致振动控制中的效果进行研究。其恢复力方程如式（1）所示：

Fn=kq3（1）

式中：Fn——NES非线性恢复力；

k——NES的非线性刚度；

q——其位移响应。

1.2 涡激力模拟

桥梁结构的涡激振动产生机理是当风流经过主梁或吊杆时，气流在主梁上下表面或吊杆尾流中不停交替脱落，导致在结构物两侧边缘处产生周期性交替脱落的气流漩涡，这将使结构受到一个横向的周期荷载作用。而当结构的涡脱频率与其的某一阶固有频率相近时，该阶振动模态将会由于发生共振而产生大幅涡激振动，称之为涡激共振。

桥梁涡振是一种限幅振动，很少会导致桥梁发生结构性承载力破坏。然而，桥梁发生长期的涡激共振，却会使得结构振幅长期过大，导致桥梁结构耐久性降低。同时，涡振会造成桥面晃动，影响行车体验感、舒适性，极易诱发交通安全事故。

1.3 桥梁结构-NES动力学模型

本文采用3次刚度NES对大跨度桥梁涡激振动进行控制，由于桥梁竖向涡振往往以单一振型出现，因而可通过引入相应模态振型坐标，将涡激力作用下桥梁结构-NES动力系统简化为两自由度的振动体系，其示意图如图1所示。

随后采用四阶龙格库塔法，可对上述非线性微分方程进行求解分析。

2 NES参数优化策略

NES控制效果的好坏，取决于其质量m2、非线性刚度k2以及阻尼系数c2的选取。既往研究表明，NES质量m2与主结构质量m1比值越大，其控制效果越好，但随着质量比的不断增加，其对控制效果的增益程度也逐渐降低。同时，过大的质量，将会给NES的施工及使用维护造成很大困难，不利于实际使用。因而，工程中实际采用质量阻尼器进行结构振动控制时，需综合考虑工程减振效果、施工难度及经济性等因素，其质量比常控制在＜1.5%，因此本文采用质量比m2/m1为1%。

NES非线性刚度k2以及阻尼系数c2的选取是其发挥优异控制效果的关键，当参数选取得当时，NES能发生靶向能量传递现象，显著降低结构响应。而当参数选取不当时，不仅会弱化NES减振性能，某些情况下甚至会放大结构响应，对结构安全产生不利影响。由此，本文通过数值搜索方法对非线性能量阱进行参数优化分析，寻找最佳的非线性刚度k2以及阻尼系数c2取值。

以桥梁主结构的最大位移幅值作为判断NES性能的指标，则数值搜索方法的参数优化目标可设置为：使桥梁主结构的最大位移幅值最小。具体作法为：通过MAT LAB软件编写k2以及c2参数取值的二重循环，使其逐一遍历设定范围内所有可能的（k2，c2）取值组合，避免出现漏算，错过最佳参数组合；对每一个取值组合，将k2，c2对应取值代入式（3）、式（4）中，通过四阶龙格库塔法求解桥梁主结构时程响应，而后将时程响应幅值及其所对应的参数组合（k2，c2）存入数据库中进行比选，最大位移幅值最小者所对应的（k2，c2）参数取值即为最佳的NES非线性刚度以及阻尼系数取值。

3 NES在大跨桥梁涡振控制中的应用实例分析

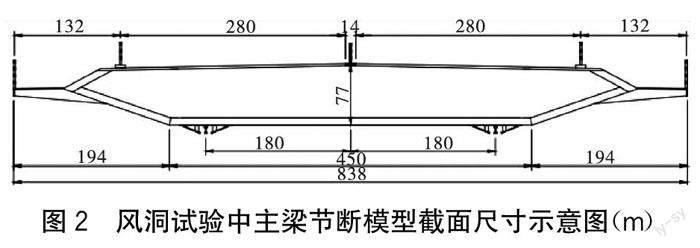
本文以国内某大跨度钢箱梁悬索桥为例，对NES的涡振控制性能进行分析。该桥梁主跨为1 196 m，桥面宽24.5 m，桥梁中间设有中央护栏，主梁为钢箱桁架组合梁断面。由于桥梁跨度大，且桥位地形气候复杂，使桥梁受到风荷载的影响显著。为此，研究人员制作了桥梁几何缩尺比为1∶40的主梁节断模型，该风洞模型使用的断面尺寸如图2所示。由于桥梁的涡致振动常由单一模态主导，因此该风洞模型是基于实际桥梁第一阶竖弯模态而设计，将其通过弹簧系统悬挂于风洞中，以模拟目标频率。该桥梁模型质量为43.2 kg，阻尼比为0.39%，刚度为14.34 kN/m，斯脱罗哈数St取0.059，桥梁模型第一阶竖弯模态的自振圆频率为18.22 rad/s。

随后开展了风洞试验［10］，试验结果表明：当风攻角为+7°时，桥梁出现了明显的竖向涡激振动现象。随着风速逐渐增加，在2.08～2.74 m/s的风速下，发生了第一次竖向涡振；在3.78～5.83 m/s风速下，则出现第二个涡振区间。值得注意的是，在风速达到5.67 m/s时，结构振幅最大，约达6 mm。而后，随着风速进一步增加至6 m/s，桥梁的竖向涡振逐渐消失。以上研究结果表明，桥梁受到风荷载引发的涡致振动影响显著，需要采取相应措施确保其安全性和可靠性。

为此，本节将采用NES对该桥梁的涡致振动进行控制。首先基于上述桥梁动力参数，利用第3节中数值搜索方法对NES进行参数寻优，在质量比m2/m1为1%的情况下，寻找使得桥梁主结构的最大位移幅值最小的非线性刚度k2及线性阻尼系数c2的最佳组合参数，最终得到最优参数k2=64.87 N/m，c2=3.87 Ns/m。随后对该最优化NES的桥梁涡致振动抑制效果进行分析。

如图3所示，绘出了结构在无控制时以及装配NES装置时的风速-振幅对比曲线图。由图3可知，无控结构存在两段明显的共振响应风速区间，分别为［1.9，2.8］m/s以及［3.7，5.8］m/s区间，其中振幅最大值出现于风速为5.65 m/s时，达到了5.91 mm。而当采用NES进行减振控制时，结构涡振响应迅速下降，其振幅最大值为0.94 mm，较无控制时降低了约84%，说明NES起到了很好的减振控制效果。

如图4（a）、图4（b）所示分别为风速U=2.38 m/s及U=5.54 m/s时采用NES控制以及无控制时的桥梁结构位移时程曲线，这两个风速均位于桥梁出现了明显的竖向涡激振动现象时的风速区间。由图4可知，当U=2.38 m/s时，结构时程曲线均为周期响应，NES减振效果明显；当U=5.54 m/s时，可以看出，无控制时结构响应仍为周期响应，采用NES控制时结构响应出现了幅值调制现象，此时为准周期响应，NES造成准周期响应的原因是由于其存在着非线性刚度，并且随着非线性性质进一步增强，还可能出现混沌响应。非周期响应的出现，将有助于NES进一步提升能量传递效率，实现更高效的结构减振效果。

4 结语

本文研究了非线性能量阱（NES）在大跨度桥梁涡致振动控制中的应用。首先基于模态分析建立了涡激力下桥梁结构-NES动力学模型，随后通过数值搜索方法提出了NES参数设置及优化策略，得出了使桥梁主结构最大位移幅值最小的NES非线性刚度及阻尼参数取值组合。最后，以国内某大跨度钢箱梁悬索桥为背景，模拟研究NES的涡振控制效果。结果表明，在无控制时，桥梁风速-幅值曲线上存在两个明显的竖向涡激共振风速区间，而装备NES装置后，能够有效抑制桥梁结构的涡激共振响应，使其响应幅值较无控制时降低了约84%。此外还发现，NES在幅值较大的共振响应附近可能产生准周期响应，这是由于其存在强非线性刚度导致的，在设计时需加以考虑。本文的研究成果可为相关工程提供理论和实践指导，尤其对于解决大跨度桥梁涡致振动问题具有重要意义。

参考文献：

［1］郭 健，钟陈杰，吴继熠，等.西堠门大桥涡激振动特征分析［J］.工程力学，2023，40（S1）：39-45.

［2］张文学，陈 伟，李文平.东京湾大桥风振与控制［J］.世界桥梁，2005（4）：60-64.

［3］王志诚，许春荣，吴宏波.崇启大桥主桥钢箱梁TMD系统设计参数计算研究［J］.土木工程学报，2015，48（5）：76-82.

［4］刘志彬，谭 平，王菁菁，等.新型非对称惯容NES减震控制性能研究［J］.振动与冲击，2023，42（2）：116-125.

［5］顾超杰.基于NES的柱体结构涡激振动特征及宽频减振机理研究［D］.扬州：扬州大学，2022.

［6］王修勇，胡仁康，邬晨枫，等.单面碰撞TMD及其桥梁涡激振动控制研究［J］.振动与冲击，2020，39（1）：169-174.

［7］杨兴森，李照宇，王绍华，等.基于非线性能量阱的桥梁振动能量采集装置的适用性研究［J］.振动与冲击，2022，41（19）：64-70，89.

［8］Younesian D，Nankali A，Motieyan M E.Application of the nonlinear energy sink systems in vibration suppression of railway bridges［C］.Proceedings of the ASME 2010 10th Biennial Conference on Engineering Systems Design and Analysis.Istanbul：ASME，2010.

［9］Vaurigaud B，Manevitch L I，Lamarque C H.Passive control of aeroelastic instability in a long span bridge model prone to coupled flutter using targeted energy transfer［J］.Journal of Sound and Vibration，2011（330）：2 580-2 595.

［10］王修勇，胡仁康，鄔晨枫，等.单面碰撞TMD及其桥梁涡激振动控制研究［J］.振动与冲击，2020，39（1）：169-174.

作者简介：黄东圳（1988—），工程师，主要从事公路工程、市政工程项目施工管理和勘察设计工作。