无应力状态法在系杆拱桥吊杆张拉控制中的应用

詹远艺　朱智宇　周群

摘要：为研究无应力状态法在系杆拱桥吊杆张拉控制中的应用，文章以某钢箱系杆拱桥为研究对象，针对其吊杆张拉控制难题，提出了无应力索长迭代求解新方法，并开展了背景工程中的实桥应用，成功解决了其吊杆张拉控制难题。结果表明：无应力控制法在系杆拱桥吊索张拉中的适用性良好，可进一步在同类拱桥吊杆张拉控制中进行推广应用。

关键词：钢箱；系杆拱桥；施工控制；无应力；吊杆张拉

0引言

下承式系杆拱桥是拱桥建设领域的一大创新，主要应用于一些建筑高度受限、地质条件较差但又需要较大跨径的地方，尤其在一些城市桥梁建设工程中，非常受到青睐。然而，系杆拱桥与其他有推力的大跨度拱桥施工方法不一样，最大的区别在于系杆拱桥需要通过张拉吊杆完成体系转换，吊杆的张拉控制也是整桥施工最核心的环节，直接影响整座桥梁成桥内力状态［1-2］。

目前对于索力张拉控制主要有倒拆法、正装-倒拆迭代法和无应力状态法等3种控制方法，前两种控制方法以索力控制为主，但受吊杆张拉顺序、吊杆张拉索力、环境温度等因素影响较大，易造成最终成桥状态与理论设计状态偏差较大，施工控制难度较大［3-6］。无应力状态法则直接建立施工状态与成桥状态之间的关系，不随结构体系和外荷载的变化而变化，避免了施工过程的影响，很好地解决了系杆拱桥分阶段施工的结构问题，尤其在索结构桥梁施工控制中应用最为广泛。

本文以某施工中的钢箱系杆拱桥为研究对象，探讨无应力状态法在系杆拱桥吊杆张拉中的应用，为背景工程施工提供技术保障，为类似工程提供借鉴。

1 工程背景简介

某城市跨河流主干路桥梁，主桥采用跨度为140 m的钢箱系杆拱桥，桥面宽15 m，计算跨径为136 m，矢跨比为1/5.0，拱轴线采用抛物线，主拱圈、横撑均采用等截面钢箱结构，桥面系纵横梁均采用工字钢结构，均为Q355钢。桥型立面如图1所示。

全桥吊杆共设置15对，间距为9.0 m，上下游对称布置，依次编号为Z1-Z8（拱脚至跨中），均采用1 860 MPa级别的索体，型号为15.2-19。

为保证高精度的成桥索力及成桥线形，本项目考虑采用无应力状态控制法进行吊索张拉，探讨无应力状态法在系杆拱桥吊杆张拉中的应用。

2 有限元模型的建立

为探讨无应力状态法在系杆拱桥吊杆张拉中的应用，本文采用Midas Civil软件建立结构整体有限元模型，如图2所示。

吊杆采用只受拉索单元进行模拟，其余主梁结构均采用一般梁单元进行模拟。考虑到实际施工的满堂支架主要提供竖向承载力，因此采用只受压弹性支撑模拟满堂支架。全桥共计423个节点，405个单元。

3 吊杆无应力索长的求解分析

一般而言，无应力状态法计算结构合理施工状态是采用无应力状态量参数进行控制，保证中间施工无应力状态量与合理成桥无应力状态量保持一致，成桥状态与施工过程无关。本文吊杆无应力张拉控制以吊杆无应力索长作为控制量，即控制吊杆实际施工下料长度。

根据材料力学计算公式，吊杆无应力索长计算公式为：

l=l0+（Nl0/EA）（1）

式中：l——吊杆有应力索长（mm）；

l0——吊杆无应力索长（mm）；

N——吊杆力（kN）；

E——弹性模量（MPa）；

A——吊杆截面积（mm2）。

由式（1）分析可知，已知吊杆力及吊杆有应力索长，即可计算出吊杆无应力索长。因此，吊杆实际施工控制可以设计成桥索力作为吊杆已知索力，设计成桥索长作为吊杆有应力索长，即可求得吊杆无应力索长。

当然，吊杆作为索单元，应考虑其轴向刚度与索力、索长、自重等所成的非线性关系，即吊杆弹性模量E在索单元计算中并非是固定值，一般考虑采用等效弹性模量法进行迭代计算。

为解决这一非线性难题，本文提出一种吊杆无应力索长有限元迭代计算方法，具体计算过程如下：

（1）建立全橋一次落架整体有限元模型，采用多点弹性支撑法、刚性横梁法或未知荷载系数法对成桥设计索力进行复核计算，保证所建模型与原设计基本一致。

（2）取设计成桥索力（一般由设计方提供）作为各吊杆索单元初拉力，采用NewZon-Raphson法进行吊杆非线性（几何非线性）分析，求解出吊杆无应力索长。

（3）取（2）中计算得到的吊杆无应力索长作为其索单元计算时无应力索长初值，同样采用NewZon-Raphson法进行吊杆非线性（几何非线性）分析，求解出各吊杆索力；与设计成桥索力作比对，求出差值，再反向加在上一步各吊杆索单元初拉力上，作为下一步各吊杆索单元初拉力。

（4）重复（2）、（3）的迭代计算，直至计算得到的成桥索力及无应力索长误差满足精度要求。

经过多个算例验证，基于以上迭代计算得到的成桥索力误差控制在＜2%即可满足吊杆无应力索长前后两次长度差值＜1 mm，此精度完全满足实际施工控制精度要求。

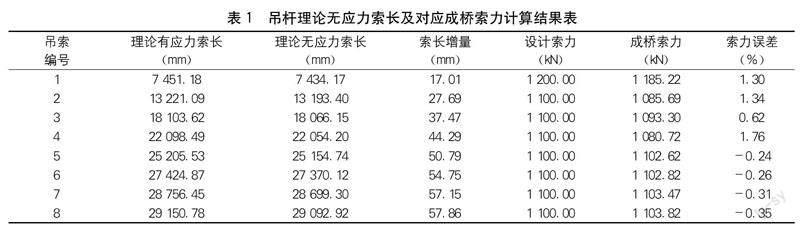
基于以上迭代算法，以设计图纸上各吊杆理论索长（即理论有应力索长，由吊杆在拱肋内上锚点算至横梁底锚垫板底面）为例，求得各吊杆无应力索长及其对应求得的成桥索力如表1所示。

由表1分析可知，经多次迭代计算后（一般4、5次就能满足精度要求），吊杆成桥索力误差已控制在＜2%，无应力索长前后两次计算差值最大为0.95 mm，已达到施工控制精度要求。

4 吊杆无应力张拉控制分析

基于前文吊杆无应力索长迭代计算方法即可求得全桥各吊杆高精度的无应力索长，下文将在此基础上以背景工程为研究对象，进行吊杆无应力张拉控制法的实桥应用，总结归纳吊杆具体无应力张拉控制过程如下：

（1）根据设计图纸、拱肋实际成拱标高、桥面标高、预拱度等，精确计算成桥状态下各吊杆实际索长（即实际有应力索长，由吊杆在拱肋内上锚点算至横梁底锚垫板底面）。

（2）根据实际有应力索长及前文迭代计算方法，精确计算出各吊杆实际无应力索长。

（3）统一控制吊杆伸出量为25 cm（為方便量测，一般以伸出量20 cm或25 cm进行控制），并计入吊杆下料长度中，即吊杆下料长度等于吊杆实际无应力索长与吊杆伸出量之和。

（4）根据现场实际情况，制定施工最为方便的吊杆张拉顺序进行吊杆张拉，以每根吊杆伸出锚垫板的伸出量25 cm进行控制。

以上4个主要步骤即吊杆无应力张拉控制的核心过程。步骤1及步骤4相关注意事项如下：

步骤1中对实际拱肋及桥面系拼装完成后的实际成拱标高、桥面标高等测量精度要求非常高，重点是对吊杆孔位进行精确测量，在一些不易测量的位置可以考虑转点，但一定需要保证测量数据的精度，以及计算结果的准确性。

步骤4对于吊杆伸出锚垫板的伸出量25 cm也需要进行严格控制，且尽可能采用受温度影响较小的刻度尺进行量测。

基于以上控制方法及控制要求，结合现场拱肋、桥面等实测数据，求得吊杆实际无应力索长、下料长度，计算结果如表2所示。

对比表1、表2分析可知，由精确测量的拱肋实际成拱标高、桥面标高、预拱度等计算得到的成桥状态下各吊杆实际索长虽与设计图纸理论索长有偏差，但根据实际索长采用本文第3节迭代计算方法求得实际无应力索长，并以此实际无应力索长求得的成桥索力误差值仍能保证在2%以内，精度完全能满足施工要求。

此外，采用无应力状态法进行吊索的张拉控制只需要控制每根吊杆伸出锚垫板的伸出量25 cm即可保证成桥状态吊索的索力精度，与实际施工过程无关，即与吊索张拉顺序无关。下文为验证这一结论的准确性，以及验证无应力状态法在吊索张拉控制中的适应性，制定了常见的3种吊索张拉方案，通过对比最终成桥索力是否一致来进行验证，并确定本桥吊杆合理张拉顺序。具体张拉方案如表3所示。

根据以上吊杆张拉方案，建立吊索张拉顺序的正装模型，得出各方案详细计算结果如表4所示。

由表4分析可知，各吊杆张拉方案中的最终成桥索力几乎一致，且与表2一次成桥计算结果也几乎一致。由此可见，无应力状态法在吊索张拉控制中是可行的，且同时证明了采用无应力状态法得到的成桥状态只与无应力索长有关，与施工顺序无关。

此外，对比不同张拉顺序可知，虽然最终成桥状态是一致的，但不同张拉顺序对应的吊杆施工阶段最大张拉力（均在各吊杆张拉时达到最大）有所不同，表4中方案B吊杆施工阶段最大张拉力优于方案A与方案C，方案B相对更合理。

本文背景工程最终选择方案B进行吊杆无应力张拉控制，张拉过程中通过液压千斤顶油表读数及吊杆伸出锚垫板的伸出量进行索力与索长双控，以吊杆伸出锚垫板的伸出量控制为主，千斤顶油表读数为辅，最终成功完成全桥吊杆张拉。经测量，锚垫板的伸出量最大误差值≤3 mm，桥面实际成桥线形与设计线形吻合良好，最大误差≤5 mm。

5 结语

本文以背景工程为研究对象，将无应力张拉控制法成功应用于系杆拱桥吊索张拉控制中，主要对无应力索长的迭代求解方法，及无应力控制法在吊索张拉中的具体应用做了详细的阐述，实桥应用也充分证明了无应力控制法在系杆拱桥吊索张拉中的适用性及方便性，可进一步在同类桥型中推广应用。

参考文献：

［1］王家豪，张志程，徐 韬.无应力状态法在吊杆拱桥索力张拉控制中的应用研究［J］.湖南交通科技，2022，48（2）：152-155.

［2］吴海军，何 立，王邵锐，等.基于无应力状态法的大跨钢管混凝土拱桥拱肋线形控制方法［J］.桥梁建设，2020，50（6）：20-26.

［3］周 倩，周建庭，陈静雯，等.钢管混凝土拱桥扣索一次张拉索力优化改进算法［J］.福州大学学报（自然科学版），2019，47（3）：412-416.

［4］傅金龙，黄天立.钢管混凝土拱桥吊杆张拉方案优化研究［J］.桥梁建设，2016，46（4）：67-72.

［5］周小勇，吕志敏，王加辉，等.支架现浇系杆拱桥吊杆张拉方案优化［J］.中外公路，2022，42（2）：125-130.

［6］邵志向.钢箱系杆拱桥无应力状态法施工控制研究［D］.西安：长安大学，2018.

作者简介：詹远艺（1989—），工程师，主要从事桥梁设计工作。