相位噪声对数字阵列波束合成的影响研究

王 璇, 郄锦辉, 李冲霄

(中国电子科技集团公司第五十四研究所, 河北 石家庄 050081)

0 引言

与传统的模拟相控阵相比,数字相控阵在多功能一体化、瞬时多波束、高精度波束赋形、动态范围和接收灵敏度等功能、性能上有明显优势[1],因此近些年被越来越广泛地应用于各种通信、雷达与电子对抗系统中[2]。 相位噪声作为最主要的射频损伤之一制约着不同系统应用的核心性能,对于通信系统,积分相位噪声(Integrated Phase Noise,IPN)影响宽带通信信号的信噪比(Signal to Noise Ratio,SNR);对于雷达系统,强杂波单边相位噪声可能会淹没微弱的目标回波;对于电子对抗系统,相位噪声则直接决定系统的瞬时动态范围。 因此,研究相位噪声在数字阵列合成中的影响,对于采用数字相控阵体制的系统应用有重要意义。

通过主动利用数字阵列的可调节自由度,结合分布化器件之间的独立性,数字阵列能够通过去相关获得多种系统性能增益[3]。 文献[4-6]分别验证了谐波抑制、杂散抑制以及虚假镜像抑制等系统增益,同时相关研究验证了这种阵列合成增益同样对相位噪声有效。 文献[7]分析了多通道采样器时钟抖动的合成特性。 文献[8-9]仿真了相位噪声合成对误差矢量幅度(Error Vector Magnitude,EVM)的影响。 文献[10]验证了同步本振合成的相位噪声增益。 大部分研究主要关注了阵列合成对于性能提升的作用,少部分研究进一步分析了提升所付出的代价。 文献[11]分析了相位噪声对阵列方向图波束指向和副瓣电平的影响。 文献[12]理论分析了交叠阵列相位噪声对于干扰抵消器性能的影响。

为了对不同架构的数字阵列进行理论分析和性能评估,需要构建一个更完整、高效的分析方法。 基于相位噪声的统计特性以及实际阵列架构的实现,通过借鉴阵列激励误差所采用的概率方法,引入子阵本振复用结构差异,以一维均匀线阵(Uniform Linear Array,ULA)为例,理论推导了以相位抖动、子阵划分以及方位扫描角度为变量的期望功率方向图和期望SNR 表达式,进一步通过数值分析更完整地展示了相位噪声对数字阵列合成的影响。

1 相位噪声在数字阵列中的建模

数字阵列接收信号的模型可由式(1)表述[13],假定阵列共N个通道,考虑采样步长为L,共Q个空间源信号[14]。 X 为N×L维接收信号矩阵,A 为N×Q维空间矢量矩阵,S 为Q×L维源矩阵,N0为N×L维噪声矩阵[15],即:

假定考虑了激励误差和相位噪声的阵列空域滤波N×1 维复权值向量由u表示。u的第n个通道权值表述如下:

式中,an,ϕn,ξn,δn,ϑn分别为第n个通道理想的实数激励幅度、理想的激励相位、激励相对幅度随机误差、激励相位随机误差[16]以及相位噪声误差[17]。

阵列输出L个时间点的合成信号如下:

式中,H 为Hermiton 算子;Y 为数字波束合成(Digital Beam Forming,DBF)后信号,为1×L维向量。

进一步讨论式(1)~式(3)所引入的3 种影响性能的因素:热噪声N0、幅相激励误差(1+ξn)exp(jδn)以及相位噪声项exp(jϑn)。

N0通常被建模为N行独立同分布具有零均值的复高斯随机向量,即加性高斯白噪声(Additive White Gaussian Noise,AWGN)。 自由振荡的压控振荡器的相位噪声可描述为维纳过程,相关研究通常采用高斯模型建模[11],进而可假定不同通道间相同时刻相位噪声满足ϑn~Ν(0,σ2)[9],反映到阵列合成中的exp(jϑn)项为乘性有色的。 加性噪声以绝对功率能量的形式起作用,在低SNR 场景中为主要矛盾,会限制阵列的接收灵敏度;而乘性噪声以相对信号能量的形式起作用,在高SNR 的场景中影响较大。 同时由于是有色噪声,因此一般被定义为相对载波频率固定频偏Δf处归一化到每赫兹带宽内的相对噪声功率(Spot Phase Noise,SPN)。

在数学表达式上,相位噪声项exp(jϑn)与幅相激励误差(1+ξn)exp(jδn)中的相位误差项exp(jδn)有相同的形式,因此可以引入类似的分析方法。 用于分析激励误差对阵列性能影响的方法有3 类:蒙特卡罗仿真分析[18]、概率方法[19]和区间算法[20]。蒙特卡罗仿真对于复杂阵列结构计算量大,分析效率低,因此主要对比后2 种方法。 基于随机变量δn和ϑn的实际物理意义,相位激励误差δn是在大量通道单元间服从统计独立分布的,对于单一通道而言其误差值是确定且时不变的,同时在理想校准的前提下,校准残留相位的边界是由移相步进所限定,而ϑn则是时变且无法明确限定取值边界的,更适合引入概率方法[19]进行分析。 在进入理论推导和数值仿真前,还需要明确相位噪声模型的变量σ,以及阵列结构变量k。

为了得到随机变量ϑn的方差并方便后续的推导,需要在相位噪声功率谱密度SPN(f)(dBc/Hz)、IPN(dBc)、均方根相位误差以及抖动τjitter(10-15s)等几个等效的量之间完成转化。 通过限定的积分频偏区域[Δfmin,Δfmax],通过下式可求解单边带的IPN:

图1 给出了TI 公司宽带频率综合器芯片LMX2595、ADI 公司集成收发器芯片ADRV9009 以及Xilinx 公司RFSoC 本振源在相应载波频率的SPN(f)曲线。

图1 集成本振源的相位噪声相对功率谱密度Fig.1 Phase noise relative power spectral density of integrated local oscillator

根据芯片所给出的SPN(f)并限定频偏积分区间为100 Hz~100 MHz,可计算得到IPN,以及τjitter,计算结果如表1 所示。 集成芯片的τjitter在几十到几百飞秒量级,转化为均方根相位误差在0.1°~0.7°。

表1 集成本振源IPN 性能Tab.1 IPN performance of integrated local oscillator source

进一步讨论积分区间的贡献,对于LMX2595 积分区间从100 Hz~1 kHz 增加到100 Hz~100 MHz,依次计算得到的结果如表2 所示。 远端SPN(f)低于-150 dBc/Hz,其对最终τjitter的贡献可以忽略不计,这意味着在考虑相位噪声对阵列波束合成的影响时,可以认为阵列满足窄带假设,波束合成方向图在积分区间保持不变。

表2 LMX2595 不同积分区间相噪性能对比(9 GHz)Tab.2 Comparison of phase noise performance of LMX2595 in different integration intervals(9 GHz)

完整的阵列相位噪声模型还需要考虑通道间本振源的相关性。 引入文献[2]中以均匀子阵划分为变量的分析方法,ULA 阵列实际架构如图2 所示,假定通道数为2K个,每个子阵包含2k个通道,整个阵列的子阵数为2K-k,子阵内部通过射频与时钟分配网络共用变频本振和采样时钟,子阵间变频本振和采样时钟严格同步。

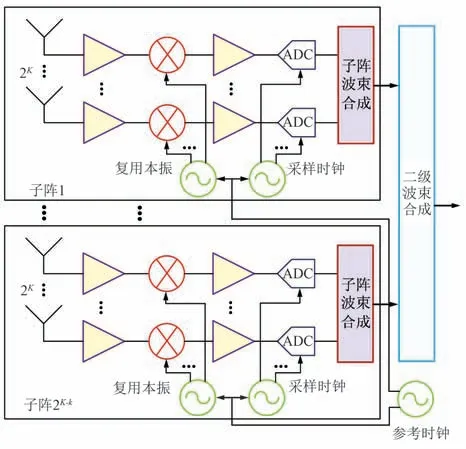
图2 子阵内通道复用本振源的数字阵列架构Fig.2 Digital array architecture of channel multiplexing local oscillator in subarrays

相应考虑阵列第n个通道变频本振与时钟所引入的相位噪声,在不同子阵间ϑn相互独立,相同子阵内ϑn完全相关,因此有:

式中,corr(ϑi,ϑj)为ϑi与ϑj的相关系数。

此外,单独通道相位噪声方差可能由多个相互独立的相噪源贡献,比如图1 中通道内的本振源与时钟源,可通过得到总的相位噪声方差,在后面的推导和仿真中只考虑σ2total,不再进行详细的区分。

2 引入相噪的阵列SNR 与功率方向图

基于上面所构建的阵列相位噪声模型,可以进一步推导SNR 和功率方向图。 完整讨论噪声N0,幅相激励误差(1+ξn)exp(jδn)以及相位噪声项exp(jϑn)超出了所关注的范围,因此在后续推导分析中,仅针对相位噪声项exp(jϑn)求解。 简化后,ULA 幅度方向图的频域F(θ)及时域形式F(t,θ)如下:

式中,Cn为相位梯度;ω为角频率。

阵列的时域输入x(t,θ)与输出信号y(t,θ)如下:

式中,⊗表示时域卷积;x(t,θ)假定为宽平稳复数基带随机过程。

定义SNR(θ)为理想波束合成输出功率Pideal(θ)与相位噪声合成功率Perror(θ)的比值:

式中,E[·]表示数学期望。 分子理论项yideal(t,θ)与分母误差项yerror(t,θ)可以通过式(11)的变换得到:

首先推导Pideal(θ),

式中,()∗代表复共轭;期望项为x(t-Cn/ω)的自相关Rx(γ,θ),γ=(Cn-Cm)/ω。

在频域进一步简化式(14)可得:

接下来求解Perror(θ),按式(14)方式展开得到3项求和。 3项分别由来表示。

式中,第1 项即为式(15);第2 项推导得到:

第3 项推导得到式(18),该项即为要求解的功率方向图与Rx(0,θ)的乘积:

在求解SNR(θ)时,式(12)中分子分母中的Rx(0,θ)会相互抵消,因此在后面的推导中不再考虑该项,利用以ϑn为变量正余弦函数的统计量:

以及式(8) 所描述的本振复用相关性,可以将Perror(θ)的3 项写成矩阵形式,以最复杂的第3 项为例,即矩阵形式的功率方向图为:

式中,向量G 和D 分别为由式(22)和式(23)给出的1×N维的行向量,且均为θ的函数。

而M 为N×N维矩阵,利用式(18)~式(20),可得M 中的元素Mi,j为:

通过类似的推导过程,可以得到矩阵形式的Pideal(θ)与Perror(θ)|2,利用式(12)可得到SNR(θ)。其中最重要的情况为波束指向方向的SNR(θB),采用均匀幅度加权,得到:

在接下来的仿真分析中,主要利用本节得到的SNR(式(25))以及功率方向图(式(21) ~式(24))针对不同的τjitter以及k值进行分析。

3 不同相噪性能与子阵结构的仿真分析

基于所得到的解析式,以一个K=3,即由23=8 个天线单元及数字接收通道所构成的ULA 阵列进行分析,以讨论相位噪声对阵列波束合成性能的影响。 假定ULA 阵列的工作频率为10 GHz,并满足相控阵窄带假设(即在相位噪声积分带宽内方向图不变),最大扫描角度为90°,对应单元间距为15 mm。 假定子阵内单元数,即共用本振的单元数为2k,其中k∈[0,1,2,3],ULA 使用2K-k个独立本振。 使用抖动τjitter(10-12s)描述IPN 并作为仿真变量在[0.57,3.43,6.3,9.16,12.03]取值。 2 种典型的架构为k=3 与k=0:当k=3 时,ULA 共用同一个本振,对应的相位噪声完全相关,可描述为集中化本振;当k=0 时,8 个通道分别使用不同的本振,对应的相位噪声完全独立,可描述为分布化本振。

首先,使用式(25)分别以2k和τjitter为X轴变量得到的SNR(θB)曲线如图3 和图4 所示。 从整体趋势上来看,k减少对应本振去相关程度的增加,同时获得SNR 增益,τjitter的增加对应SNR 恶化。

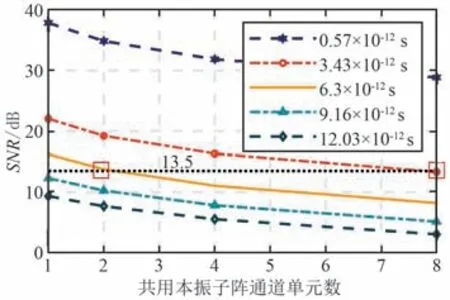
图3 本振分布化对应的阵列SNR 曲线Fig.3 Array SNR curve corresponding to local oscillator distribution

在图3 以SNR=13.5 dB 绘制一条直线,该直线同τjitter=6.3×10-12s以及τjitter=3.43×10-12s 分别相交于k=1(对应子阵包含2 个共用本振通道)与k=3(对应子阵包含8 个共用本振通道)点,这意味着采用低性能分布化本振,能够实现与集中化高性能本振相同的整阵SNR 性能,这也是文献[1]所分析的数字阵列分布化所带来的主要优势之一。

图4 中标出了τjitter=0. 57×10-12s 以及τjitter=12.03×10-12s 不同k值下的SNR 数值。 对于τjitter=0.57×10-12s,本振逐渐分布化所带来的SNR 增益为3 dB,而随着τjitter增加,分布化所带来的SNR 增益会降低,因此对于相位噪声较差的链路,分布化所带来的SNR 增益会低于预期。

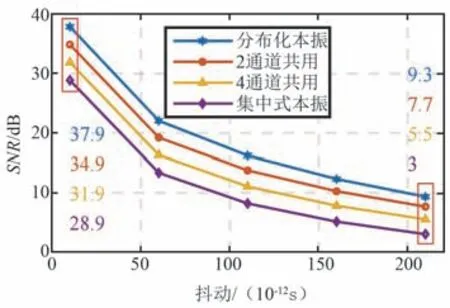
图4 抖动增加对应的阵列SNR 曲线Fig.4 Array SNR curve corresponding to increased jitter

使用式(21)可以得到图5 和图6 所示的波束指向法线方向时的阵列合成归一化功率Pnorm(θ)方向图的期望曲线。 整体上,随着本振分布化以及τjitter(θ)量增加,Pnorm(θ)畸变程度增加,主要体现在主波束增益下降、幅瓣电平抬高及零深回填。

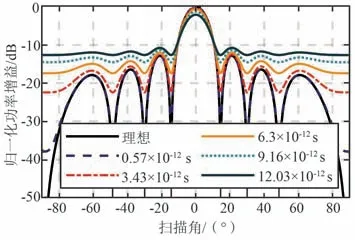
图5 抖动增加对分布化阵列Pnorm(θ)的影响Fig.5 Effect of increased jitter on distributed arrays Pnorm(θ)

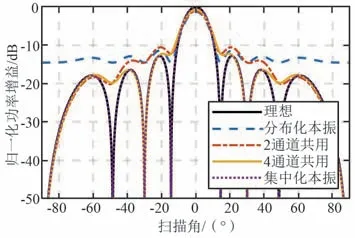
图6 分布化对阵列Pnorm(θ)的影响(τjitter=6.3×10-12s)Fig.6 Effect of distribution on array Pnorm(θ)(τjitter=6.3×10-12s)

集中化本振与理想Pnorm(θ)重合是由于相位噪声带来的瞬时抖动会同时作用于所有通道,不会造成通道间相对与理想激励相位梯度的相位偏差,因此不会造成的Pnorm(θ)的变化。 相互独立的相位噪声合成在数学建模形式上等同于激励相位误差,如果相位误差同相位噪声有相同的均值和方差,那么得到的Pnorm(θ)与分布化本振情况完全相同,但二者的实际物理含义和对系统的影响并不相同。 激励相位误差可认为是静态的,反复测试得到的Pnorm(θ)是相同的,而相位噪声所导致的相位抖动是动态的,得到的Pnorm(θ)是数学期望,在某些状态下副瓣电平有可能超出Pnorm(θ)所得到的期望曲线[19],同时所对应的扫描角度在理想方向图中可能对应副瓣也可能对应零点。

直觉上,由于分布化所导致的法线增益恶化与SNR 提升相互矛盾,实际上对比所定义的Pnorm(θ)表达式(21)与SNR 表达式(12)可知,法线功率增益恶化是相对于空域滤波所接收到的外界噪声以及系统所引入的加性热噪声而言,而式(12)所定义的是针对相位噪声所导致的SNR 恶化,二者并不矛盾。

注意图6 中,k= 1(2 通道共用),τjitter= 6. 3×10-12s 所造成的零深回填并没有发生在所有零点,这同图2 所示的本振共用结构有关[9]。 使用a,b,c,d 分别来表示ULA 所使用的4 个独立本振,图4所采用的8 通道本振复用排列结构为‘aabbccdd’,即临近单元共用本振。 图5 显示了另外4 种本振复用排列结构所得到的Pnorm(θ)对比,4 种结构分别为:‘ababcdcd’ ‘abcdabcd’ ‘abcddcba’ ‘abbacddc’,不同结构对应了式(21)与式(24)中M 矩阵内等于1 元素位置的不同。 对于无幅度加权的扫描指向,式(22)向量单元全为1,式(23)向量单元全为0,因此由式(21)扫描方向E[F(θB)2]的值为M矩阵所有元素求和,因此复用结构的变化并不会影响扫描指向的功率增益;而空间调零的实现基于该方向来波信号到达不同阵列单元的相位反向,当存在相位噪声导致的相位误差时,这种反相抵消条件被破坏,导致调零回填,相关单元间抵消所产生的调零点受到的影响较小。 为了更好地显示不同结构对零深回填的影响,图7 仿真分析采用波束指向θB=-40°方向。

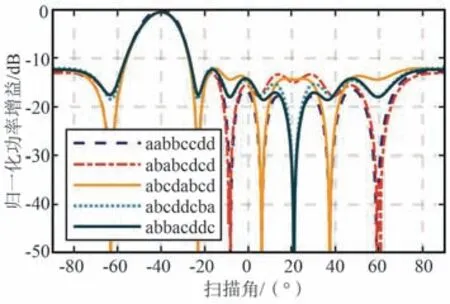
图7 不同本振复用结构对零深回填位置的影响Fig.7 Influence of different local oscillator multiplexing structures on nulling filling position

为了进一步分析相位噪声对阵列抗干扰的影响,依然保持θB=-40°波束指向角度,对阵列引入副瓣抑制30 dBc 的切比雪夫幅度加权,同时使用文献[22]所采用的空间调零方法在θ=29°引入调零点。

分布化本振结构不同抖动性能下的零深回填如图8 所示。 如果采用分布式的本振,即便是τjitter=3.43×10-12s 的相位噪声性能指标,也会导致副瓣性能的严重恶化,理论上-30 dBc 的副瓣抑制度恶化为只有-20 dBc。

图8 分布化本振结构不同抖动性能下的零深回填Fig.8 Nulling filling under different jitter performance of distributed local oscillator structure

不同本振复用结构对零深的影响如图9 所示,τjitter=6.3×10-12s 从集中化到部分相关再到分布化的过程中,零深从理论上的大于-50 dBc 最终恶化到-20 dBc。

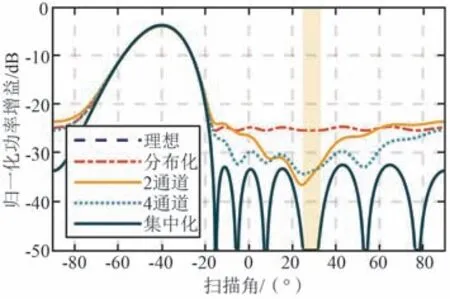
图9 不同本振复用结构对零深的影响Fig.9 Effect of different local oscillator multiplexing structures on nulling

表3 以二维矩阵的形式给出了不同分布化程度(即不同k值)和抖动性能下θ= 29°的调零深度变化。

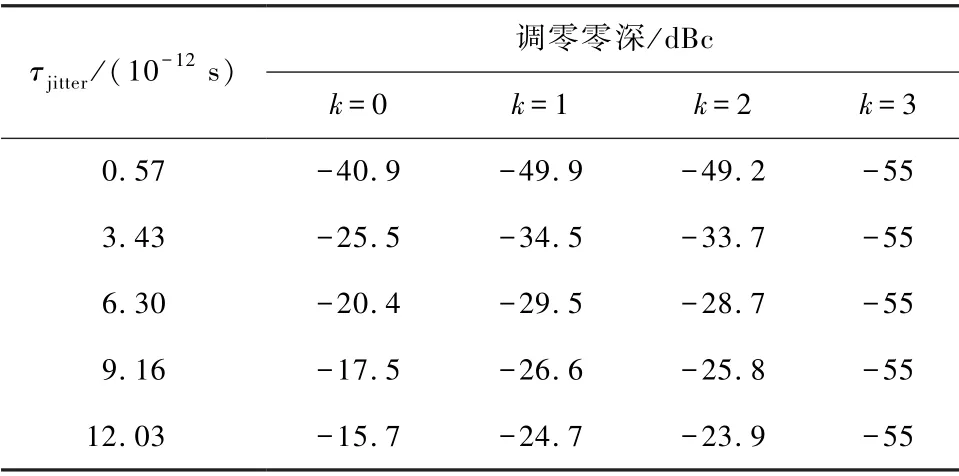
表3 相位噪声合成后阵列的调零零深Tab.3 Nulling depth of array after phase noise synthesis

数字阵列的优势之一是能够实现高精度的幅相控制,从而实现高精度的波束指向和干扰抑制。 综合上述仿真分析可知,相位噪声均值为0 的特性不会影响波束指向,但对于干扰抑制的性能影响较大。 要充分发挥数字阵列高精度幅度加权、干扰调零乃至波束赋形等性能,需要合理地设计本振乃至时钟分配网络,在空域特性和时频域特性之间进行折衷考量。

4 结束语

构建了基于概率建模的相位噪声对DBF 阵列性能影响的分析方法,与蒙特卡罗仿真方法相比,采用理论推导得到的SNR 与功率方向图闭式表达式进行性能评估要更高效,特别是对于复杂的阵列结构和系统建模。 为了简化讨论过程,主要针对ULA和相位噪声这一单一射频损伤进行了论述,但所构建的方法并不限于此,能够进一步扩展到二维扫描阵列,并能够适用于同时考虑幅相激励、空间误差、热噪声及量化噪声的情况,因此对于采用数字相控阵体制的系统设计与评估具有一定实用价值。