基于CNN 和GRU 的农产品价格预测模型研究

李洁琼, 刘 振

（1.西安职业技术学院基础课教学部, 西安 710077；2.西安文理学院化学工程学院, 西安 710065）

中国是农业大国, 确保农产品价格稳定一直是政府关注的重点, 也是宏观调控的难点。由于农产品销售周期不同, 价格波动较大[1］。物价波动不仅影响人们的生活质量和农民收入, 还会引发社会性问题。随着大数据、人工智能等技术快速发展, 农产品价格预测成为可能[2］。如何准确、实时地预测农产品的短期价格, 是数学建模长期以来不断探索的研究领域。因此, 对农产品价格预测模型进行研究具有重要的现实意义。

目前, 许多国内外学者对农产品价格预测模型进行了大量研究, 并取得了一些优异的成果。张顺利等[3］将长短期记忆神经网络用于苹果价格预测模型, 比传统预测模型能更好地预测均值绝对误差、均方误差和均方根误差。范俊明等[4］提出了一种基于LSTM 深度学习的大豆期货价格预测模型, 比传统模型具有更高的预测精度, 为大豆期货价格预测提供了新思路。王会娟等[5］提出了一种基于TEI@I 方法的玉米期货价格预测模型, 相比于传统预测模型, 该方法可以有效地进行玉米期货价格预测, 与实际值较为接近。刘斌等[6］将分布式神经网络用于苹果价格预测。结果表明, 该方法可以有效反映苹果价格波动情况, 为苹果市场稳定发展提供一定的参考。但上述研究在实际使用中存在准确率低和效率低等问题, 适应性有待进一步提高。

本研究提出了一种结合卷积神经网络（Convolutional neural network, CNN）和门控循环单元（Gated recurrent unit, GRU）的农产品价格预测模型。通过CNN 获取局部特征, 通过GRU 获取数据的时序依赖, 然后将CNN 和GRU 获得的特征连接起来, 通过解码器获得预测输出。通过试验与传统模型进行对比分析, 验证了模型的优越性。

1 理论概述

1.1 卷积神经网络

全连接神经网络由于参数较多, 导致计算速度慢和过拟合等问题[7］。因此, 需要一种新的网络结构, 而卷积神经网络可以做到。卷积神经网络作为深度学习的典型算法之一, 它由多个卷积层、顶部的全连接层以及相关的权重和池化层组成[8］。这种结构允许卷积神经网络使用图像处理中常用的二维输入数据结构, 而时间序列展开类似于图像（图1）。卷积层的作用是提取输入数据的特征。池化层是进行特征选择和信息过滤。全连接层是卷积神经网络的全连接层, 相当于常规前馈神经网络的隐藏层。

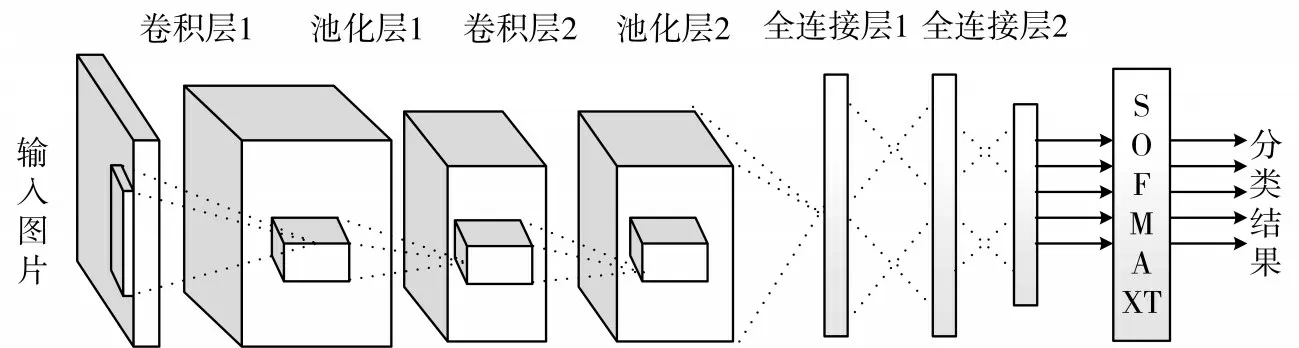
图1 卷积神经网络结构

1.2 门控神经网络

GRU 是在2014 年提出的递归神经网络的门控机制[9］。GRU 与长短期记忆网络相比去掉了一个遗忘门。与循环神经网络相比, GRU 做了以下改进。

1）重置门和更新门如公式（1）和公式（2）所示[10］：

式中,rt和zt分别为重置门和更新门；W为权重；b为偏置参数；ht为t时刻隐藏状态；it为t时刻的输入；σ为sigmoid 函数。

2）候选隐藏状态如公式（3）所示[11］：

GRU 通过重置门和更新门来确定剩余的隐藏信息, 作为下一时刻的预测输入。

2 模型建立

2.1 评价指标

由于农产品价格预测的高度随机性和不确定性, 存在预测误差在所难免。这些误差可以帮助人们更好地了解预测模型并不断优化预测方法。常用的指标包括均方根误差（RMSE）、平均相对误差（MAE）、平均绝对百分比误差（MAPE）和R2决定系数。

1）均方根误差如公式（5）所示。如果预测值等于实际值, 则均方根误差为0。均方根误差越大, 值越大[13］。

2）平均相对误差如公式（6）所示, 平均相对误差能较好地反映预测值误差的实际情况。当预测值与真实值完全相等时平均相对误差等于0, 平均相对误差越大, 值越大。

3）平均绝对百分比误差如等公式（7）所示。值越接近0, 模型的预测值越接近实际值, 平均绝对百分比误差越接近1, 模型与实际值的偏差越大[14］。

4）R2决定系数如公式（8）所示。值越接近1, 模型的预测值越接近实际值, 反映预评估的符合程度[15］。

式中,On和分别为n时刻的实际值和预测值；M为预测样本总数；O～为实际值的平均值。

2.2 模型的整体结构

农产品价格波动与时间相关, 因此, 需要一个获取时间序列潜在规律的神经网络。GRU 可以有效捕捉数据的时间依赖性, CNN 可以从全局的角度找到数据规律。为此, 本研究提出了一种结合CNN 和GRU 的混合模型, 利用CNN 获取局部特征, 使用GRU 获取数据的时序依赖, 然后将二者获取的特征进行拼接, 通过解码器得到预测值输出。模型的整体预测结构如图2 所示。

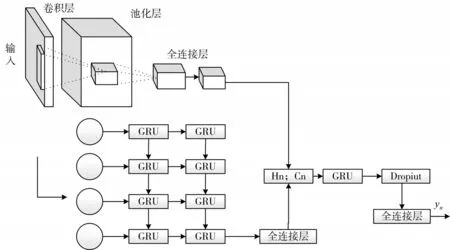
图2 模型的整体预测结构

数据集中的每组数据都有时序性, 这与GRU 模型的工作方式是一致的, 因此模型使用GRU 来捕获每个时间序列的依赖关系。以滑动窗口中得到的数据为输入, 定义第n个窗口中的数据为xn, 对GRU 第n个窗口的隐藏状态进行更新, 如公式（9）所示[16］。

式中,fe为GRU 更新函数。

将xn输入到模型中时, 通过重置门和更新门进行处理, 如公式（10）所示：

式中, 输入xn经过线性变换, 即乘以权矩阵Wir, 上一刻的ht-1与对应权重Whr相乘；Sigmoid 函数将这两部分结合起来, 压缩到[0, 1］；获取hn决定信息,rn遗忘信息。

更新门与重置门类似, 只是将权重改为Wiz和Whz, 两部分通过sigmoid 函数合并, 压缩到[0, 1］, 获取hn和rn用于更新。

然后通过公式（12）计算当前记忆内容。

这个过程使用之前获得的更新门输出, 将输出乘以前一时刻的记忆内容, 得到前一时刻的信息并发送到当前时刻。此外, 更新门的输出处理后乘以当前两部分的叠加就是最终的输出内容。

解码过程将卷积网络提取的特征cn与编码得到的隐藏层状态hn拼接, 作为解码器的初始状态。

式中,fd为编码器的GRU 更新函数。

解码器的初始状态是将GRU 状态和CNN 提取的特征拼接起来, 使用前一时刻的实际目标变量数据作为初始输入y1n, 将输出循环输入GRU。

通过GRU 获取数据的时序依赖, 但无法获取不同维度和时间的特征关系, 因此需要加入卷积神经网络。

卷积神经网络通过卷积运算得到一系列特征, 使用卷积核对时间窗口中的矩阵数据进行卷积, 卷积是在h×h的窗口中进行卷积, 如公式（15）所示：

卷积核处理是通过设置好的卷积核对数据进行点乘校验, 得到相应的结果。但是, 数据在一次卷积操作中往往无法处理完全, 需要滑动到下一个位置进行处理, 按照设置的步长滑动。

经过卷积运算, 提取出特征向量cn。卷积过程中使用ReLU 激活函数提高网络的稀疏性, 使提取的特征代表性越强, 泛化能力越强, 求导速度越快。ReLU 函数可以作为卷积层的激活函数。函数的定义如公式（16）所示[17］：

在该模型中, 特征向量经过池化层得到局部最优特征, 如公式（17）所示：

步骤1：对价格历史数据进行预处理。

步骤2：通过CNN 获取局部特征, 通过GRU 获取数据的时序依赖, 作为解码器的输入。

步骤3：优化集成学习模型。采用COCOB 优化器, 将正则化因子引入全连接层, 添加Dropout 层实现模型优化, 防止过拟合。

步骤4：以处理后的数据为输入, 训练模型, 不断调整参数直到最优。

3 结果与分析

3.1 试验参数

通过试验与传统模型进行对比分析, 验证模型的优越性和合理性。农业数据来自中国蔬菜网, 数据在剪裁后输入模型中。试验环境为联想PC, 操作系统为Ubuntu 18.04.1 64 位, Intel i5 82050u CPU, 1.6 GHz×8 主频, 8 GB 内存[18］。

模型参数：输入窗口为30 px×9 px, 时间长度为30 min, 卷积核为3 px×3 px, GRU 隐藏层维度为30维, 编码器GRU 数为2 个, 解码 器GRU 数为1 个。数据集按7:3 的比例划分为训练集和测试集, 通过训练集对模型进行训练。

3.2 试验分析

为验证模型的优越性和有效性, 将学习率设为0.001, 迭代次数设为10 000 次, 以白菜价格近10 年的数据为输入数据, 建立模型, 通过训练集对模型进行训练。在Tensorboard 中获得训练集损失函数图。从图3 可知, 随着迭代次数的不断增加, 训练集损失值逐渐降低。训练集损失值在迭代达3 000 次左右时开始趋于平稳, 达到预期效果, 再增加迭代, 训练集损失值也非常平稳。

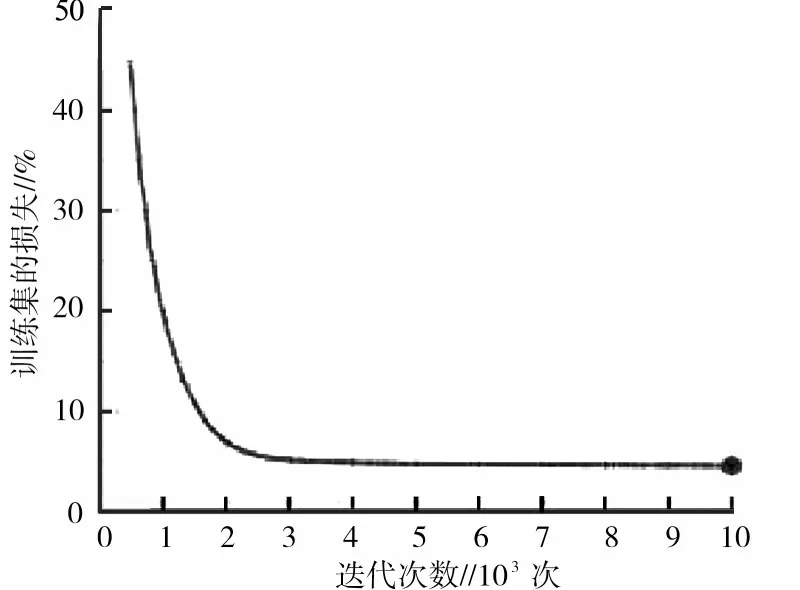
图3 训练集损失变化

为了验证模型的有效性, 将本研究构建的模型与LSTM 模型、GRU 模型进行了比较, 并预测未来某一天数据。从表1 可知, 本研究构建的预测模型表现较好,RMSE为10.04%,MAE为6.31%,MAPE为3.001 2%,R2为0.960 8。对比模型中, GRU 模型性能较好, 各项指标均优于LSTM 模型。

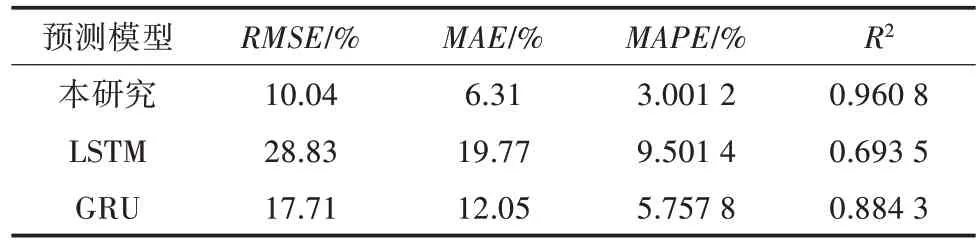
表1 评价指标结果

为了测试本研究构建模型的优越性, 使用训练好的模型对测试集进行了预测, 共1 095 d。不同模型测试数据集的预测结果如图4 所示。与其他模型相比, 本研究构建的模型预测值与实际值基本一致。LSTM 模型和GRU 模型的预测与实际值有一定的偏差, 其效果比本研究构建的模型差很多, 这表明本研究构建的模型表现良好。

不同模型预测前7 天数据RMSE对比如表2 所示。随着预测天数的增加, 本研究构建的模型、LSTM 模型和GRU 模型的预测性能变差。但与LSTM 模型、GRU 模型相比, 本研究构建模型的RMSE波动较小, 性能下降的速度最慢, 表明本研究构建的模型在测试集上的效果最优。

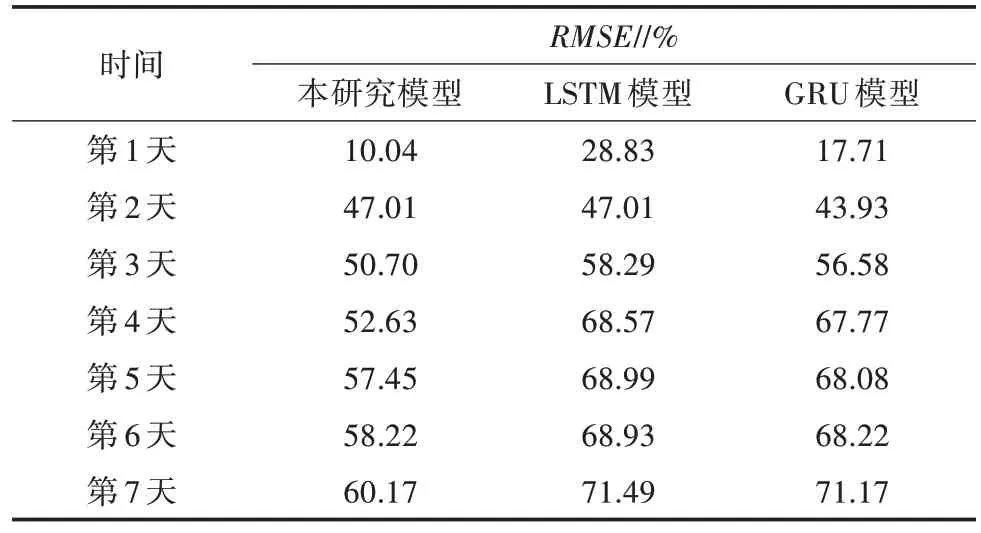
表2 RMSE 对比

在预测多天数据时, 随着预测天数增多, 训练所需的时间不断延长, 第8 天的预测时间相比于第7 天增加明显, 但预测性能不断下降。因此, 预期天数的最佳赋值为7 d。这是因为本研究构建的模型可以使用历史数据对农产品价格进行预测, 但随着预测时间的增加, 数据包含的有效信息不断减少, 导致误差不断增加, 直到信息被完成挖掘。总的来说, 通过农产品历史数据, 本研究构建的模型可以有效地进行短期预测, 误差也满足要求。

4 小结

本研究提出了一种结合CNN 和GRU 的农产品价格预测模型。通过CNN 获取局部特征, 通过GRU获得数据的时序依赖, 然后将CNN 和GRU 获得的特征连接起来, 由解码器获得预测输出。研究结果表明, 本研究构建的模型预测性能优于LSTM 模型和GRU 模型, 可以有效地进行短期预测。如果预测时间超过7 d, 预测时间会明显增加, 性能也会逐渐下降。从目前的试验设备和数据规模来看, 该研究尚处于起步阶段, 模型仅具有较高的短期预测性能。基于此, 逐步增加更多的价格影响因素, 不断完善和优化模型将是下一步工作的重点。