基于模糊多属性决策的旅游目的地选择

曾涵棓 金检华

（西南石油大学理学院，四川成都 610500）

一、研究背景及研究目的

国内旅游业逐步恢复，机票、火车票搜索和预订量骤增，旅游景区和大型主题乐园纷纷重新开放。

成都，不仅是中国西部商业、金融、旅游的中心，也是世界休闲之都、美食之都、世界优秀旅游城市。因此，本研究试图从选择成都市旅游的游客角度出发，探究成都市旅游目的地选择的主要因素及其影响，最后提出促进成都旅游业发展和游客目的地选择的建议。

二、理论基础

（一）三角模糊数的概念及运算性质

（二）熵权法的概念及运算

在信息论中，熵是不确定性的一种度量[2]。熵的大小与不确定性的大小成正比关系，包含的信息量随着熵的增加而增加。如果要判断一个事件的无序性和随机程度，可以依照熵的特性，计算熵值来衡量。利用熵值判断某个指标的离散程度，离散程度越大说明该指标对综合评价的权重越大。熵权法是一种客观赋权法，仅依赖于数据本身的离散性，计算过程如下：

首先，判断输入矩阵中是否存在负数元素，若存在则需要重新标准化到非负区间。正向化后的矩阵：

即有n 个样本，m 个属性，对该矩阵进行标准化得到矩阵Z，Z 的元素：

如果Z 中存在负数，则需要对X 使用另一种标准化方法得到：

其次，计算第j 项属性下第i 个样本的比例，并将其视为计算相对熵时使用的概率。若标准化后的矩阵：

则计算概率矩阵P 的公式：

最后，计算各个属性的信息熵与信息效用值，并采用归一化方式获取每个属性的熵权。对于第j 个属性，其信息熵的计算公式：

信息效用值的定义：

每个属性的熵权：

（三）TOPSIS 法的概念及运算

为了解决多属性决策问题，有学者提出TOPSIS方法[3]。该方法的优势在于充分利用原始数据的信息，将各备选方案分别与正负理想解相比较找出最接近正理想解且又远离负理想解的方案，计算结果可以准确地反映评价方案之间的差距。首先是确定正理想解和负理想解，二者分别表示如下：

三、三角模糊多属性决策TOPSIS 方法研究

（一）问题描述

令M={1,2,…,m}，N={1,2,…,n}，设备选方案为Xi，属性为Uj，属性权重为Wj。备选方案Xi的属性以三角模糊数的形式给出。

（二）属性的确定

根据我国居民选择旅游目的地时主要考虑的因素，选择以下6 个属性进行分析：目的地景观形象（U1）、目的地排队等候时间（U2）、到达目的地交通便利程度（U3）、目的地餐饮条件（U4）、目的地消费水平（U5）、目的地服务水平（U6）。

（三）方法步骤

步骤1：通过式（17）、式（18）对三角模糊矩阵进行规范。

式（17）中，I1表示效益型属性的下标集，I2表示成本型属性的下标集。将初始三角模糊决策矩阵转化为规范化的三角模糊决策矩阵[4]。

步骤3：利用式（10）计算概率矩阵P，并利用式（11）计算各属性的信息熵ej，利用式（12）计算信息效用值dj，再利用式（13）计算各属性的权重wj。

步骤4：由属性权重向量W 和规范化处理后的三角模糊决策矩阵，构造加权规范三角模糊决策矩阵。

步骤5：由式（14）、式（15）确定正负理想方案I+和I-。根据式（16）进行计算，得到各备选方案Xi与正负理想方案I+和I-相比较的相对相似度S(Xi,I+)和S(Xi,I-)。

步骤6：因为最优方案要尽量接近正理想方案I+，远离负理想方案I-，接着利用式（20）计算得到各备选方案Xi与正负理想方案I+和I-相比较的整体相对相似度：

步骤7：将各备选方案Xi按照RS(Xi)值由大到小的顺序进行择优排序。

（四）实例研究

某前往成都旅游的游客利用一天时间选择成都市内一景点进行游玩，根据初步筛选，选择了以下6 个景点Xi(i=1,2,3,4,5,6)，分别为青城山-都江堰旅游景区、成都大熊猫繁育研究基地、西岭雪山、成都欢乐谷、黄龙溪、洛带古镇，根据以上研究选择6个属性Uj(j=1,2,3,4,5,6)，其中U1、U3、U4、U6为效益型指标，U2、U5为成本型指标，专家利用三角模糊数的形式，根据6 个指标对6 个景点进行评分并给出评价值。经过整理，得到初始三角模糊决策矩阵，初始三角模糊决策信息如表1 所示。

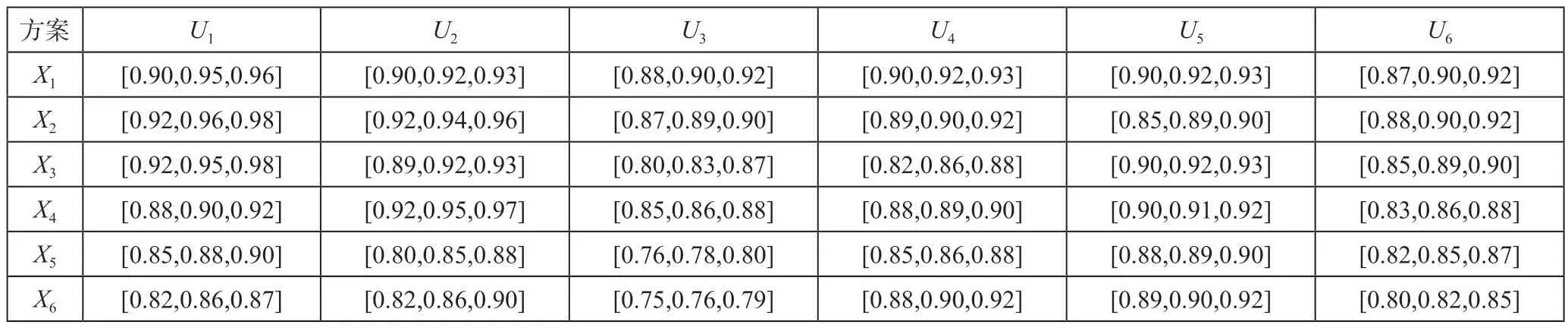
表1 初始三角模糊决策信息表

运用三角模糊多属性决策TOPSIS 法解决该实例问题，具体步骤如下。

表2 规范化的三角模糊决策信息表

步骤2：使用中心区域法进行模糊数实数化，去模糊化的决策信息如表3 所示。

表3 去模糊化的决策信息表

步骤3：计算熵权，各属性的熵权如表4 所示。

表4 各属性的熵权

表5 加权规范三角模糊决策信息表

步骤5：确定正负理想方案I+和I-。

I+={[0.782 6,0.833 1,0.884 2],[0.852 5,0.916 3, 0.997 8],[1.633 7,1.716 8,1.794 3],[0.277 3,0.288 7, 0.298 0],[0.102 1,0.105 4,0.111 8],[0.438 0,0.458 2, 0.484 2]}；

I-={[0.697 6,0.746 3,0.785 0],[0.773 4,0.819 8 ,0.867 6], [1.392 4,1.449 8,1.540 8],[0.252 6,0.269 9,0.282 0],[0.098 8, 0.102 0,0.105 6],[0.398 2,0.417 5,0.447 3]}。

步骤6：计算得到各备选方案Xi与正负理想方案I+和I-的相对相似度S(Xi,I+)和S(Xi,I-)和整体相对相似度RS(Xi)。

S(X1,I+)=0.9 7 5 8，S(X2,I+)=0.9 7 7 4，S(X3,I+)=0.9521，S(X4,I+)=0.9466，S(X5,I+)=0.9428，S(X6,I+)=0.9324；

S(X1,I-)=0.9297，S(X2,I-)=0.9282，S(X3,I-)=0.9524，S(X4,I-)=0.9578，S(X5,I-)=0.9623，S(X6,I-)=0.9734；

RS(X1)=0.0033，RS(X2)=0，RS(X3)=-0.0520，RS(X4)=-0.0634，RS(X5)=-0.0722，RS(X6)=-0.0947。

步骤7：由RS(Xi)值可知，X2＞X1＞X3＞X4＞X5＞X6，故最佳选择方案是X2，即选择成都大熊猫繁育研究基地对游客来说是最优的。

将本研究结果与在携程旅行网查阅的成都周边各景点热度值进行比较，Xi的热度值如表6 所示。

表6 各景点的实际热度值

Xi按热度值由大到小排序为X2＞X1＞X3＞X4＞X5＞X6，这与本文的研究结果相同，说明本文的研究方法是可行的，是具有现实意义的。

四、结论与建议

为保证旅游目的地决策的可行性和实用性，本文提出了基于三角模糊的旅游目的地决策方法。以成都市6 个旅游景点为例，通过专家对旅游目的地属性进行打分，采用熵权法确定每个属性的权重，利用TOPSIS 决策模型对旅游目的地进行排序发现，选择成都大熊猫繁育研究基地进行旅游是最符合旅游期待的。从计算结果可以看出，游客在旅行时，会更看重交通出行是否方便，这与实际情况相符，因为游客想把更多的时间花在游玩上而不是路程中，交通不便利的景点会加重游客旅游的疲惫感与烦躁感，因此相关部门应该根据实际情况增添旅游直达公共交通，更好地促进旅游业发展。其次是目的地排队等候时间的长短，过长的排队时间会消耗游客积极性，如果游玩体验与排队时间不符合，更是大大降低游客的旅游体验感，因此各景点应该合理设置检票窗口和检票流程，保证更快的检票速度，给游客带来更好的旅游体验，吸引更多的 游客。