基于RLS和BO算法的重型车载重估算研究

白晓鑫，吴春玲*,2，景晓军，杨永真

（1.中汽研汽车检验中心（天津）有限公司，天津 300300；2.天津大学 机械工程学院，天津 300072）

重型货车超限超载是造成公路桥梁设施损坏、交通事故频发和运输市场秩序混乱的重要原因。据调查数据显示，全国约50%的群死群伤性重特大道路交通事故与超限超载有关，车辆若超载50%，公路正常使用寿命将缩短80%[1]。重型车超载给我国道路运输业和人民生命财产带来了巨大的威胁。精准识别重型车超载，加强源头监管成为重型车超载治理的关键手段。近年来，随着高速公路入口“地磅”等静态称重系统的应用，重型车超载现象得到了一定程度的治理。与此同时，以过磅检查为主的重型车静态称重技术具有设备安装及后期维护成本高、部署工程量大、测试效率低、路网覆盖率低等弊端，无法对在用车辆载重进行实时测量，难以满足大规模在用车的超载管制。为解决重型车载重实时估计问题，基于车辆运行数据的重型车载重评估技术逐渐受到研究者的关注。

现有重型车载重评估技术多以整车纵向动力学为基础。林楠等[2]结合运动学模型，利用加速度传感器获取车辆行驶纵向加速度和道路坡度信息，结合带遗忘因子的递归最小二乘法（Recursive Least Squares, RLS）进行了车辆载重估算；冯源等[3]基于分段递推最小二乘估计建立了整车质量辨识算法，根据加速度分段方法，分别利用两段递推最小二乘算法得到行驶阻力及质量的估算值。NGUYEN等[4]利用智能手机采集车辆运行数据，提出了一种基于车辆加速度和速度统计特征的载重评估方法。此外，部分学者经过研究探索，提出了通过机器学习算法，学习车辆运动特征与载重之间的非线性关系，以实现对货车载重的间接估计[5]。综合来看，基于最小二乘法、机器学习等技术虽可实现重型车载重较为精准的测算，但依赖于额外加装加速度传感器来准确获取车辆三轴加速度状态参数，其估算效果往往受限于传感器的类型和精度，同时也会增加车辆成本，难以大规模推广使用。

为了准确估算重型车实际载重，解决重型车载重评估需额外安装车载加速度传感器这一难题，本文提出了基于递归最小二乘法和贝叶斯优化算法的重型车载重估算技术。

1 重型车载重评估模型

本文建立了基于重型车控制器局域网络（Controller Area Network, CAN）总线和全球定位系统（Global Positioning System, GPS）高程数据的纵向加速度和道路坡度计算方法，结合车辆纵向动力学，利用递归最小二乘法进行车辆载重估算。由于车辆加速度和道路坡度基于车速、车辆高程数据滤波—微分计算—再滤波计算得到，为选取最合理的滤波参数，本文利用贝叶斯优化算法对相关计算变量的滤波参数进行了寻优配置。本文重型车载重评估模型构建流程如图1所示。以下将对本文所采用的车辆纵向动力学、车辆加速度和道路坡度计算方法以及贝叶斯优化算法进行逐一介绍。

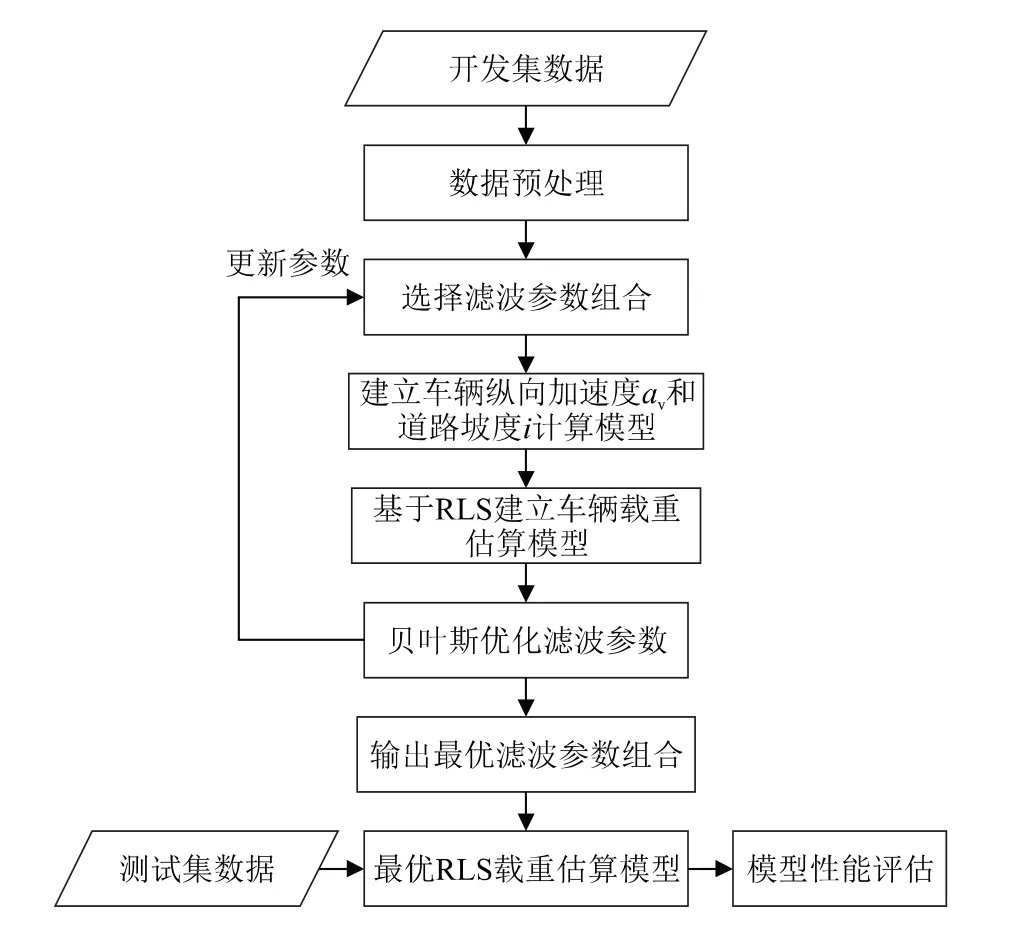
图1 基于RLS和BO的重型车载重估算模型构建

1.1 车辆纵向动力学

根据汽车理论[6]，如图2所示，整车在驱动工况下，其纵向受力平衡方程为

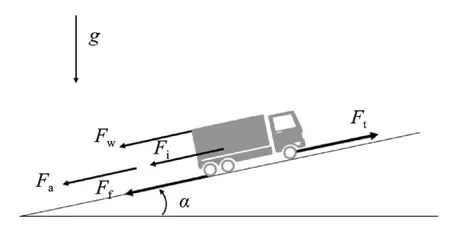
图2 车辆纵向动力学受力分析

进一步，式中各变量可由式（2）—式（6）进行计算，式中各物理量符号及含义如表1所示。

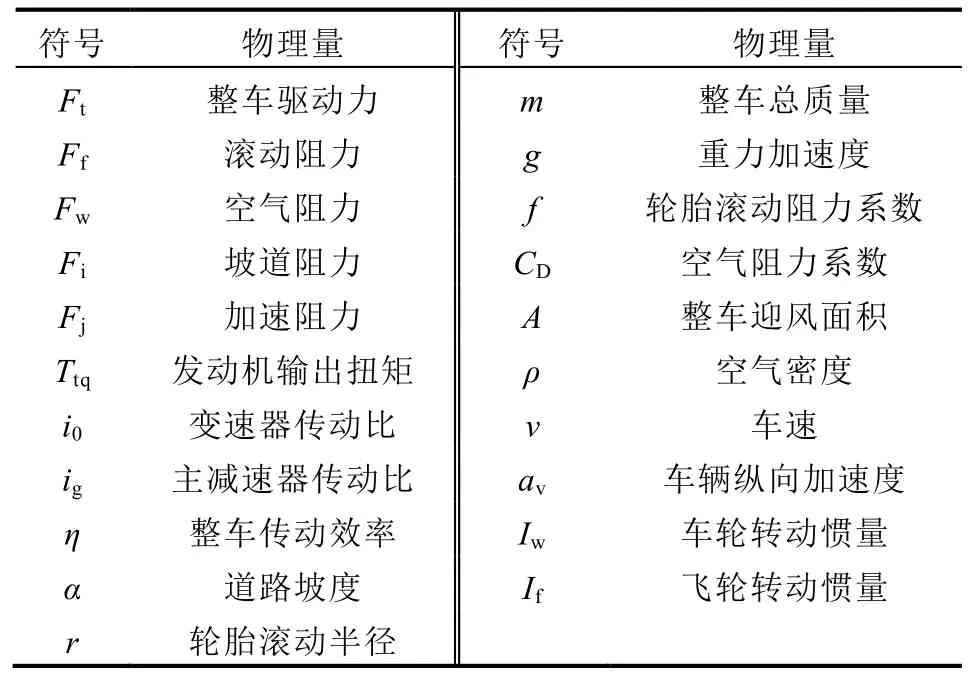
表1 计算相关物理量及含义

由此，可得

式（7）中，IW、r、If、i0、ig、η等均为整车设计参数，可由车辆制造商提供；对于载货汽车，轮胎的滚动阻力系数一般可由以下公式进行计算[7]：

而Ttq、v可通过车辆CAN总线实时获取，av可由车速差分计算得到。由于重型车特别是载货车辆货物堆放高度、方式多样，且车辆行驶过程中转弯等因素都会对迎风面积A和空气阻力系数CD产生重要的影响，用固定参数进行计算难免导致较大的误差。因此，本文将CDAρ整体作为车辆行驶过程待估算变量k，以减小上述因素对载重估算结果的影响。

整理式（7），将已知或可计算参数置于方程一侧，待估算参数m、k置于方程另一侧，可得

进一步，式（9）可简化为

式中，输入量x1=gf+gtanα+gav；输入量x2=v2；输出量。

因此，若实时计算得到道路坡度tanα和车辆纵向加速度av数据，即可利用递归最小二乘法进行车辆载重m的估算。

由于重型车在实际行驶过程中，换挡过程时间较短，换挡阶段数据难以用于载重估算；而车辆实际制动过程较为复杂，且车辆一般难以提供全面的制动信息（如轮边制动力等）。因此，本文未利用车辆换挡和制动过程数据进行载重估算。

1.2 车辆加速度与道路坡度计算

本文采用差分计算车辆纵向加速度：

对于道路实时坡度，由于车载数据的更新频率较高（1 Hz），相邻两个采样点的距离很短，可以近似认为车辆行驶的道路坡度和车辆加速度恒定。如图3所示，根据几何关系，每个采样时刻，道路坡度可近似通过下式计算：

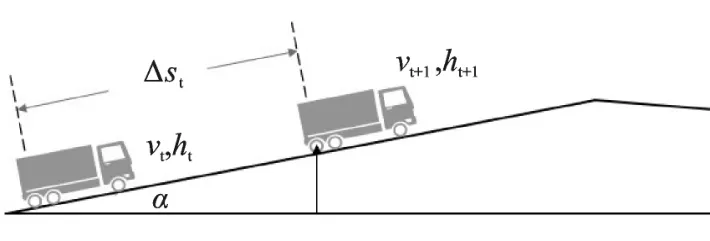
图3 实际道路坡度计算原理

式中，dh、dv、dt分别为相邻采样点的车辆垂直高度差（m）、车速差（m/s）和时间差（s）。

为远程监测重型车排放，从国六阶段排放标准开始，要求生产企业装备符合要求的远程排放管理车载终端，并在车辆全寿命期内，按要求进行车辆关键运行数据（如车速、发动机扭矩、GPS信息等）的采集和上传[9]。未来，根据车辆载重估算需要，GPS高程信息也可以从车载终端获取。

为减少通过式（11）和式（12）微分计算产生的大量异常值和高频噪声，本文采用对车速和GPS高程信号预先滤波，根据式（11）和式（12）计算加速度和道路坡度，将加速度和道路坡度计算值再滤波的两级滤波方法来获取较为真实、可靠的道路坡度。金辉等人[10]的研究同样表明，采用对车速信号进行滤波、差分、再滤波的方法可以获得具有良好实时性和精度的汽车纵向加速度。图4给出了本文车辆纵向加速度和道路坡度计算方法。

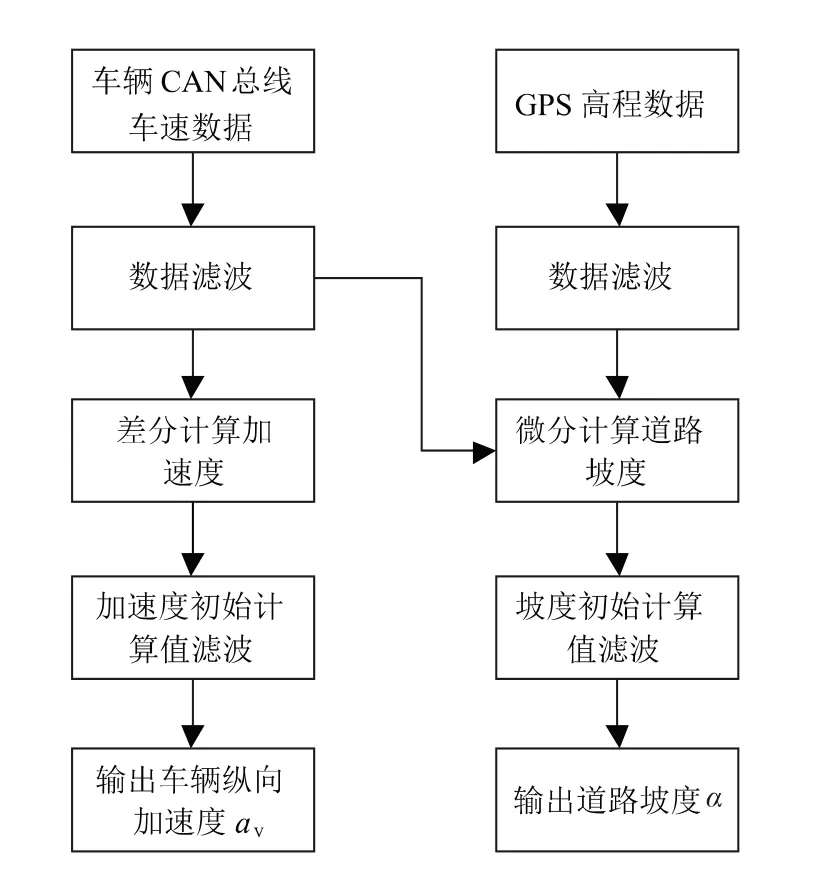
图4 车辆加速度和道路坡度计算方法

模型评估结果的准确性和泛化性能的优劣依赖于车速、高程、加速度、道路坡度计算值及其他关键计算变量滤波参数的合理选择。不同车型，上述计算变量的最优滤波参数也往往不同，通过人力无穷无尽地尝试无法实现最优滤波参数配置。因此，本文引入贝叶斯优化算法，通过对训练数据进行计算、迭代得到试验车辆上述滤波参数的最优组合。

1.3 贝叶斯优化算法

贝叶斯优化（Bayesian Optimization, BO）是由PELIKAN等学者于1998年提出的一种全局优化的方法，目前已成为机器学习领域进行超参数优化的重要方法，其本质是利用贝叶斯定律来指导搜索以找到目标函数的最小值或最大值。贝叶斯算法进行参数优化时根据样本的历史信息（先验知识）构建概率代理模型用于近似表示黑箱目标函数，利用计算得到的后验概率分布构造采集函数，通过最大化采集函数来选择下一个最有潜力的评估点[11]。

贝叶斯优化的一般过程：

1）概率代理模型先验分布的初始化；

2）计算采集函数a(x)取得最大值时的数据点x；

3）基于评估数据点x计算目标函数f(x)的值；

4）使用步骤3）中得到(x，f(x))更新概率代理模型，计算得到后验分布，作为下次迭代的先验分布；

5）重复步骤2）—4）进行迭代更新，直到达到设定的最大迭代次数；

6）输出最优数据点x。

与传统的网络搜索、随机搜索等穷举式参数优化方法不同，贝叶斯优化算法充分利用历史轮次评估结果，能在较少的评估次数下取得目标函数的最优解[12]。

1.3.1 概率代理模型

概率代理模型和采集函数是贝叶斯优化算法的核心要素。由于黑箱目标函数评估代价往往高昂且复杂，贝叶斯优化算法采用概率代理模型代理未知的目标函数，从假设先验开始，通过迭代过程逐步修正先验，得到更准确的代理模型。常见的概率代理模型包括贝塔-伯努利模型、线性模型、高斯过程、随机森林、深度神经网络等[13]。其中，高斯过程由于其高灵活性和可扩展性成为了应用最广泛的代理模型，本文选择高斯过程回归作为概率代理模型。

1.3.2 采集函数

采集函数用于选择下一组迭代参数，其表征观测点对黑箱目标函数所产生的影响，通过计算采集函数最大值来获取下一组迭代的参数。常见的采集函数包括PI（Probability of Improvement）、EI（Expected Improvement）和 UCB（Upper Confidence Bound）等。由于UCB采集函数计算简单，并且平衡了深度和宽度之间的关系，因此，本文选择基于置信边界策略的UCB采集函数。

1.3.3 目标函数

本文构造了以下目标函数f(x)，用于贝叶斯优化算法对迭代过程所选择的滤波参数进行评价：

其中，yi为数据集i车辆实际载重，ypred为数据集i递归最小二乘法估算载重，n为用于训练的数据集数量。将一组一组车速、发动机扭矩、高程、加速度和坡度计算数据的滤波参数作为目标函数输入进行训练，得到目标函数最大时所对应的一组参数组合。

2 试验与数据处理

2.1 试验平台

本文计算采用的硬件平台为Intel i7-8565U CPU和NVIDIA GeForce MX130 GPU，模型构建基于Python3.7实现，其中，参数寻优所采用的贝叶斯优化算法基于bayes_opt库实现，载重估算所采用的递归最小二乘法（RLS）基于statsmodels库实现。

2.2 数据集介绍

为采集充分数据用于载重估算模型构建和模型性能的评价，本文选取一辆N2类载货汽车，通过加载配重块的方式，针对不同载重开展了多次实际道路试验，共采集20组有效载重试验数据，如表2所示。

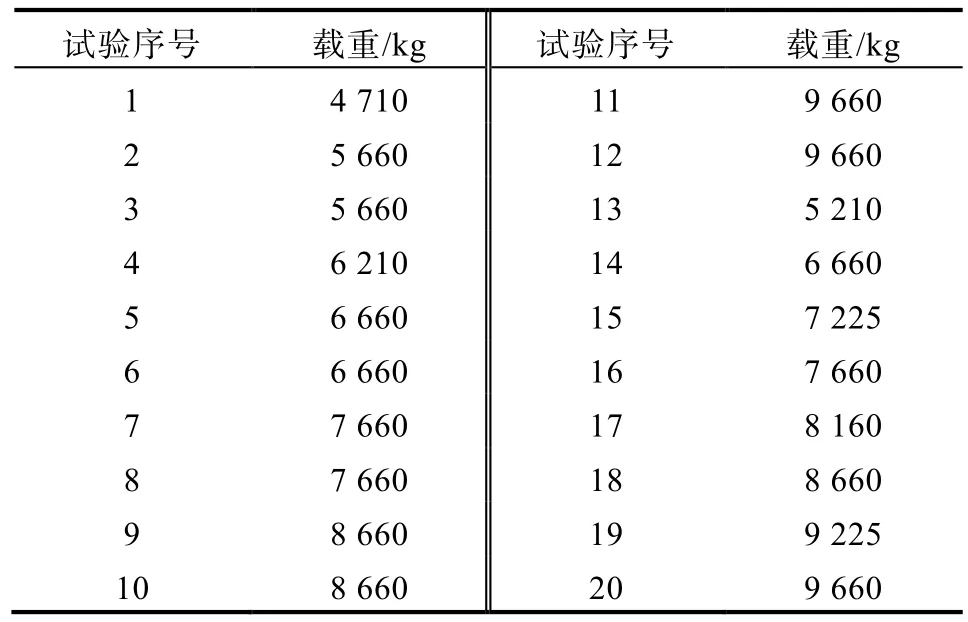
表2 载重试验信息

其中，前12次试验数据作为开发集，用于模型训练与优化；后8次试验数据作为测试集，仅用于模型有效性和稳定性的验证。根据国六排放法规要求，车载数据终端的数据采集频率应为 1 Hz[9]，为后续基于车载终端数据进行在用重型车载重估算，本文选择了1 Hz作为试验数据的采集频率。载重试验主要在天津市内进行，试验时随机选择行驶路线，驾驶员在正常车流中自然驾驶。试验车辆基本信息如表3所示。

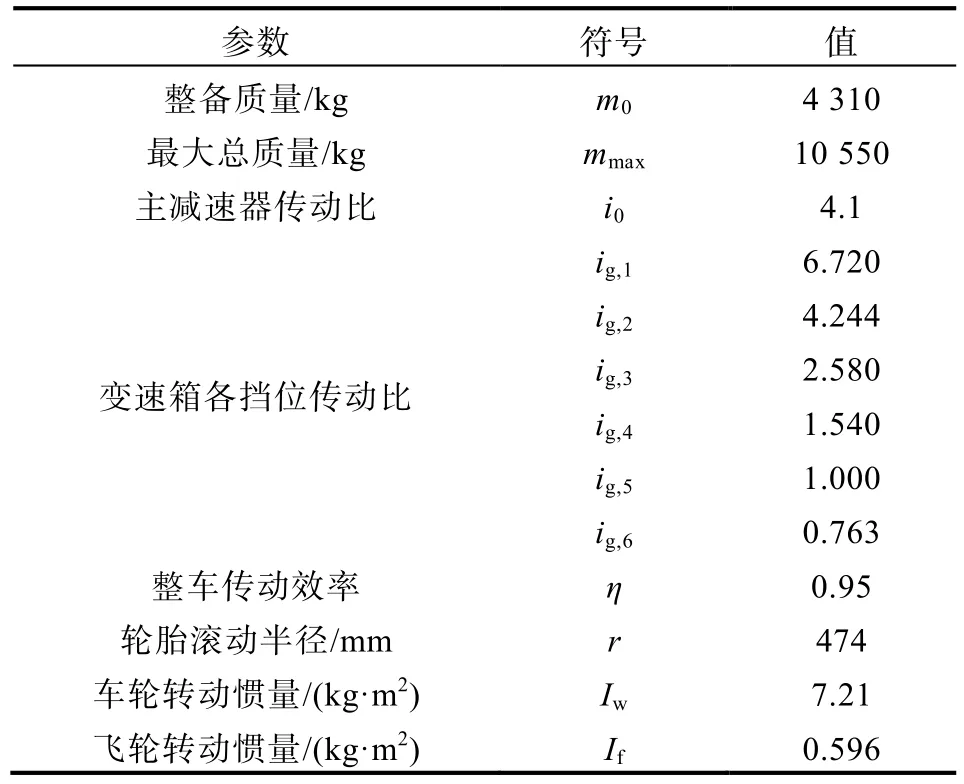
表3 测试车辆基本信息

2.3 数据处理

2.3.1 数据预处理

由于GPS信号存在不稳定情况，会导致高程数据出现异常值。因此，本文首先利用箱型图的四分位距对异常值进行检测识别和剔除处理。之后，为滤除采集获取到的车速、发动机扭矩、GPS高程数据和微分计算得到的加速度、道路坡度初始值中存在的高频噪音，采用巴特沃斯（Butterw- orth）低通滤波器来进行滤波处理。研究发现[14]，巴特沃斯数字滤波器特别适合低频信号处理，这种滤波器对于保持增益的平坦特性尤为关键，而截止频率的归一化参数wn和阶数n是其控制信号过滤效果的2个关键参数。截止频率归一化参数和阶数的选择，对车辆载重估算精度有着重要的影响。而通过理论计算很难获取实际行驶车辆不同信号最优的滤波参数，因此，本文利用贝叶斯优化算法对滤波器截止频率归一化参数和阶数进行了寻优选择。图5给出了利用贝叶斯算法进行滤波参数优化的过程。

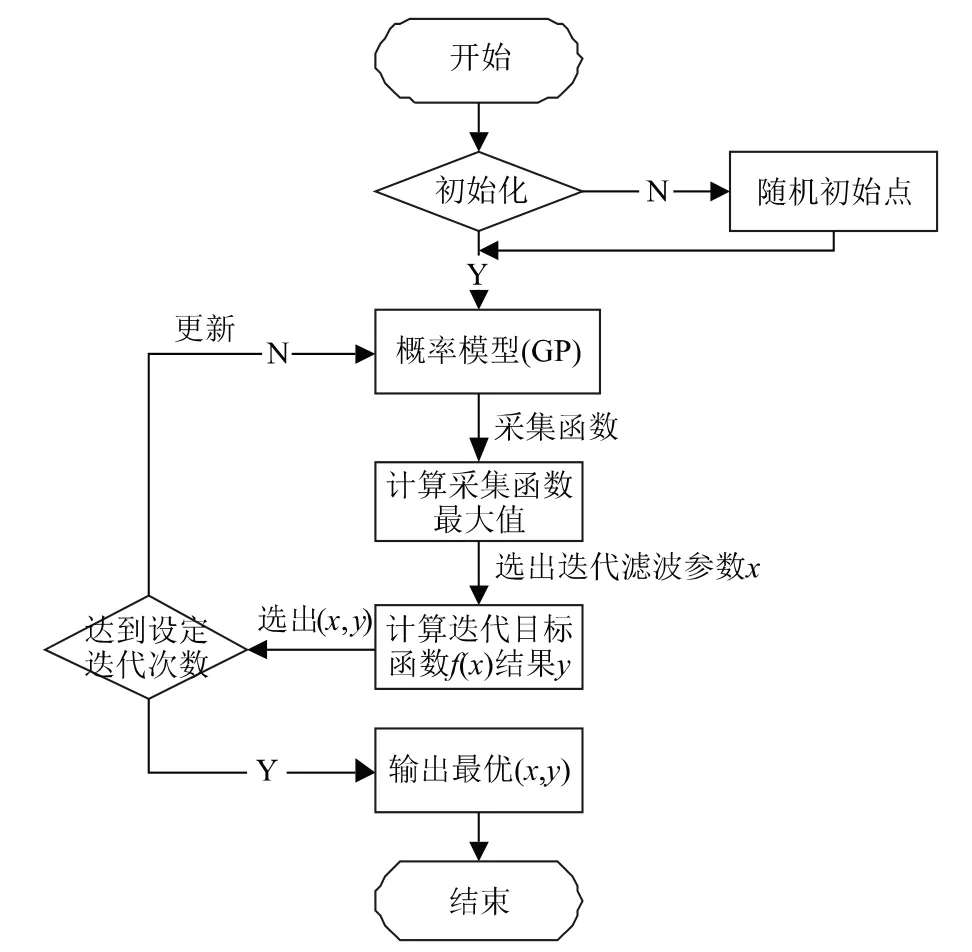
图5 贝叶斯优化过程

2.3.2 数据清洗

为进一步提高载重估算的准确性，数据滤波后进行以下数据清洗工作：

1）由于载重估算模型仅建立了车辆在驱动工况的动力学模型，无法利用车辆换挡和制动过程数据进行载重估算，根据CAN总线中车辆离合器状态和刹车状态甄别并剔除车辆制动和换挡过程数据；

2）剔除车辆低速（车速小于5 m/s）行驶数据，保证车辆处于实际行驶状态；

3）根据车辆加速度计算值分布特性，利用箱型图的四分位距对异常加速度计算值进行剔除处理；

4）根据道路设计规范[15]，行车道路设计坡度不应大于8%。因此，剔除计算值tanα大于0.08或小于−0.08的数据；

5）剔除最小二乘法估算时输入式（10）的异常值。其中，剔除x1计算值大于0.9 m/s2数据，剔除x1计算值小于0 m/s2数据，剔除yi计算值小于0 N的数据。

3 试验结果及分析

3.1 贝叶斯优化结果

基于贝叶斯优化算法，利用开发集12组试验数据，对车速、发动机扭矩、GPS高程信号和微分计算得到的加速度、道路坡度数据的巴特沃斯滤波器截止频率归一化参数和阶数进行了寻优。优化结果如表4所示。

图6给出了基于表4贝叶斯优化后的车速、高程、加速度和道路坡度计算值的滤波效果。由 图可以看出，经过巴特沃斯低通滤波后，采集信号和计算变量大量的高频噪声被滤除，特别是车辆加速度和道路坡度，信号变得更加光滑。

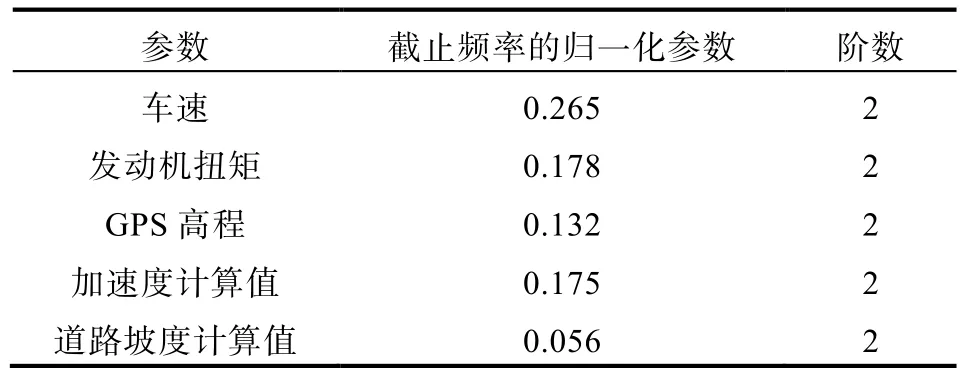
表4 滤波参数贝叶斯优化结果

图6 部分计算参数滤波效果图

3.2 载重估算结果与分析

利用测试集8组不同载重试验数据对优化完成的重型车载重估算模型性能进行了评估、验证，模型预测过程及载重估算结果分别如图7、表5所示。

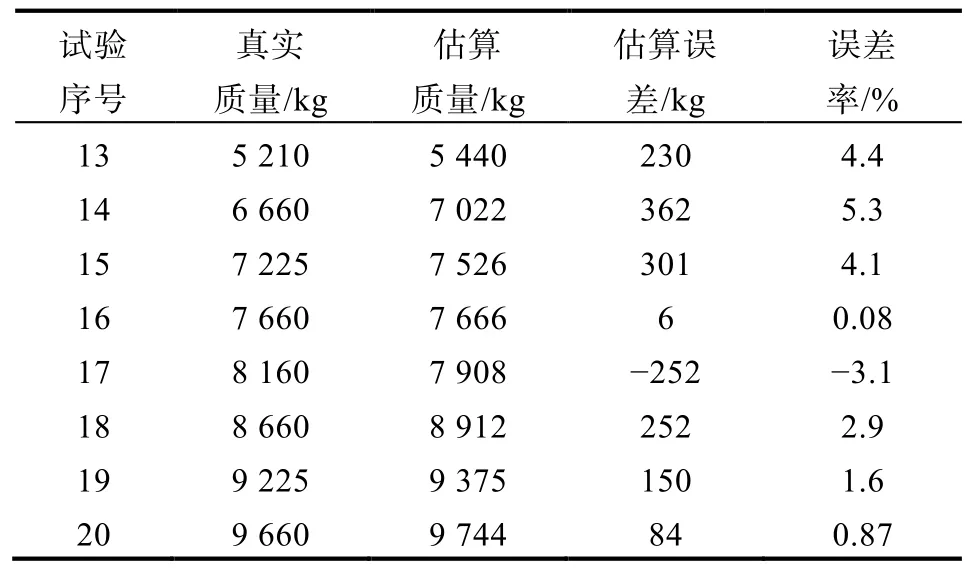
表5 模型载重估算结果

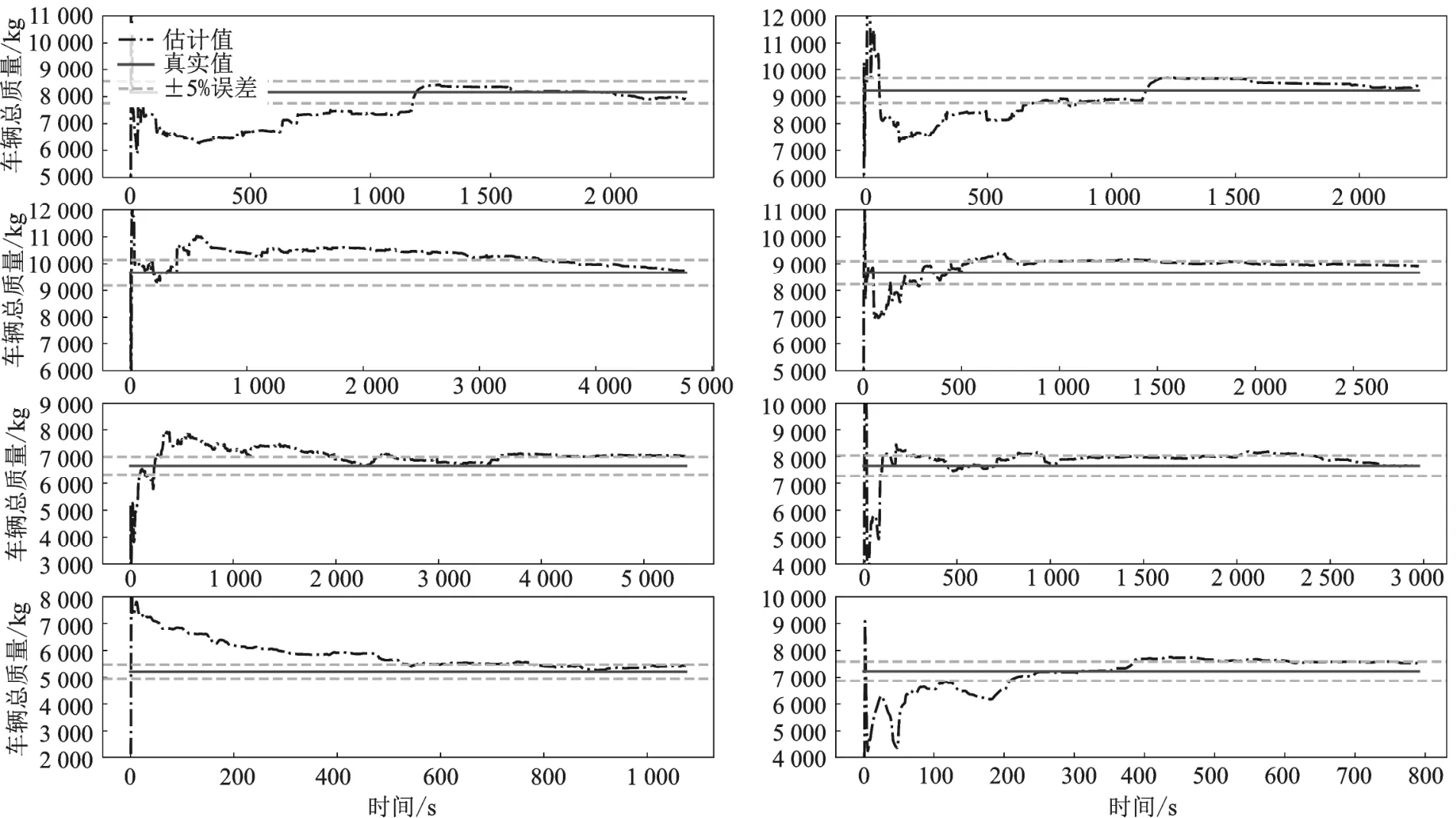
图7 不同试验数据载重估图算结果

由图6载重估算的时间序列结果可知，模型在初始估算的一段时间内，载重估算结果会有较大的波动变化，而随着试验数据的不断输入，载重估算值逐渐稳定在真实值附近，估算误差在6%以内，8次试验平均估算误差为2.8%。

此外，对测试集数据不进行低通滤波处理，其余数据处理、计算方式与本文载重估算模型均一致，单独利用RLS对处理后的数据进行载重估 算。对比了单独RLS载重估算模型与基于RLS和BO的载重估算模型计算结果，如图8所示。由图可知，单独RLS载重估算模型具有很大的估算误差，估算平均误差为45%，最高估算误差甚至达81%。这主要是由于数据处理过程中车速、GPS高程以及基于此计算的车辆加速度、道路坡度未进行滤波，使得用于进行载重估算的数据中掺杂着大量异常输入值，未能真实反映车辆实际行驶和道路状态，造成载重估算偏离真实值。这表明，车辆载重估算的精度依赖于对计算变量的数据滤波，而贝叶斯优化算法则提供了一种参数优化的高效方法。

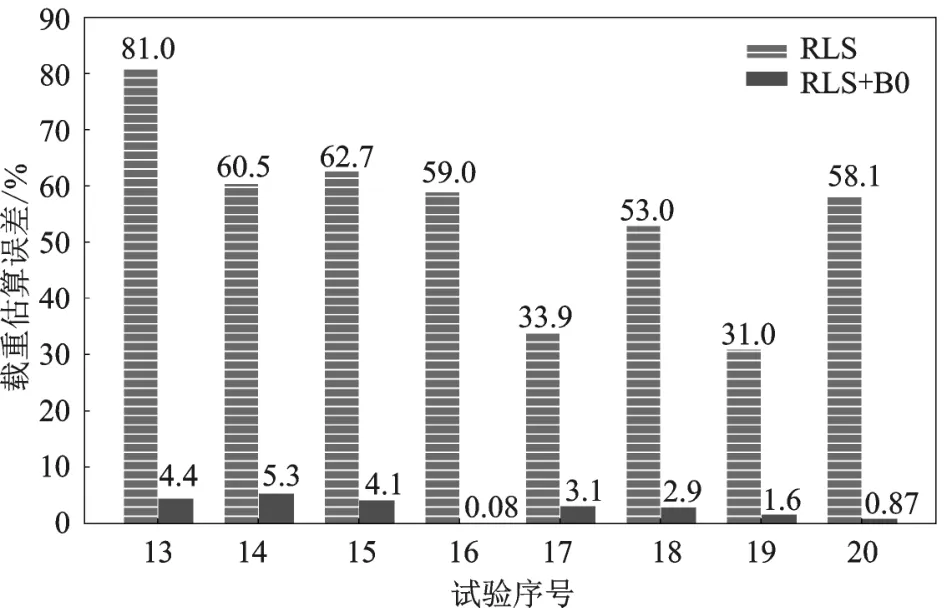
图8 不同载重模型估算结果

4 结论

1）基于重型车远程终端数据和车辆纵向动力学，开发了一种重型车载重估算的方法。试验结果表明，该方法载重估算误差在6%以内，具有良好的载重估算精度和应用便利性。

2）车辆载重估算精度依赖于贝叶斯优化算法对多计算变量滤波参数的寻优配置。试验结果表明，与仅使用RLS进行载重估算、未进行计算变量滤波相比，平均载重估算误差由45%降低至2.8%，载重估算精度得到大大提高。