二维层状热电材料研究进展*

余泽浩 张力发† 吴靖 赵云山††

1) (南京师范大学物理科学与技术学院,前沿物理与交叉科学研究院,江苏省声子工程研究中心,量子输运与热能科学中心,南京 210023)

2) (材料与工程研究院,新加坡科技局,新加坡 138634)

当今世界能源浪费巨大,其中绝大多数以废热的形式被浪费掉.热电效应可以将热能转换为电能并且没有危险物质的释放,因此热电效应的应用吸引了越来越多人的兴趣.自从石墨烯被发现以来,越来越多的二维层状材料被报道,它们通常比体块材料有着更加优越的电学、光学等物理性质,而新的理论和实验技术的发展,也促进了人们对于它们的研究.在本文中,首先介绍了基于二维材料热电性质的测量方法和测试技术,并对其测试中具有挑战性的问题进行讨论.随后对石墨烯、过渡金属硫化物、黑磷等材料的热电应用进行了介绍.最后,讨论了提升热电性能的各种策略与亟待解决的问题,并对此做出展望.

1 前言

近年来人类社会的能源需求快速增加,而极低的能源利用效率加剧了能源危机.在能源消耗过程中,绝大部分能量以废热的形式浪费掉了,如何将废热转化为有效电能对解决当前能源问题十分重要,通过实现电能和热能之间相互转化,热电材料吸引了人们越来越多的关注.为了描述热电转化,研究者用一个无量纲的量—热电优值ZT=S2σT/κ,来描述热电转化效率[1-3],其中S为塞贝克系数、σ为电导率、T为绝对温度、κ为总热导率,κ=κe+κL(κL为晶格热导率、κe为电子对热导率的贡献),并定义功率因数(PF)为S2σ,来描述热电传输中与电输运相关的物理量[4].对热电材料的研究始于20 世纪50 年代,当时人们研究对象集中在体块材料,然而其受限于较低的热电转化效率.纳米化表征技术和样品制备技术的不断发展,促进了对低维材料的研究.低维材料如二维材料具有强烈的量子限制效应[5,6],其热电性能有着显著的提高,人们对热电研究也因此进入了新的阶段.

为了进一步提高热电性能或ZT,研究者通常会选择两种方式: 1) 利用晶格缺陷或纳米结构化来降低二维材料的声子热导率;2) 利用能带工程提升并优化功率因数.然而,由于与热电性能相关的几个物理量(κ,σ,S)相互牵制,导致无法单独调控某一个物理量来提高热电优值,甚至会适得其反[7-9],例如: 由于电导率依赖载流子浓度,研究者往往通过调控材料中的载流子浓度从而提升电导率,然而,载流子浓度的提升,会使塞贝克系数下降,如图1(a)所示[9,10],因此,选择一个适合的载流子浓度达到优异的功率因数至关重要.另外,根据Wiedemann-Franz 定 律:κ e=LσT[4,11,12],其中L为洛伦兹数,可见载流子浓度的提高,会使电子对热导率的贡献显著提高,虽然在大多数情况下晶格热导率占主导作用,电子对热导率的贡献可以忽略,但电子热导率的提高并不是热电应用想要的结果,如图1(a)所示.

图1 (a) 塞贝克系数、电导率、功率因数随载流子浓度的相互依赖关系和电子热导率与晶格热导率随载流子浓度的依赖关系[10];(b) 不同维度材料的电子态密度随能量的变化关系[13]Fig.1.(a) The interdependence of Seebeck coefficient,conductivity,power factor for different carrier concentration and electron thermal conductivity and lattice thermal conductivity as a function of carrier concentration[10];(b) electronic DOS of different dimensional materials as a function of energy[13].

由于强烈的量子限制效应带来的载流子态密度差异,二维材料往往拥有优异的塞贝克系数.对于一个重掺杂的半导体来说,如果不考虑温度对载流子散射的影响,塞贝克系数可由莫特关系得到[13-15]:

其中kB为玻尔兹曼常数;σ(E) 为电导率;n(E) 为载流子浓度;µ(E) 为载流子迁移率,而载流子浓度n(E)=g(E)f(E) (其 中g(E) 为态密度,f(E) 为 费米分布函数),可知塞贝克系数与态密度随能量的变化率成正比,如图1(b)所示,因此二维材料相对块体材料往往有更大的塞贝克系数[13].除此之外,二维材料具有较高的电导率与载流子迁移率,通过载流子迁移率的调控也会提升塞贝克系数[16-18],从而达到提升热电性能的目的[19,20].对于简并半导体,莫特关系也可以简化为随其载流子浓度、有效质量、平均自由程的关系[13]:

自从二维材料石墨烯被发现以来,大量的新型二维材料相继出现,其拥有相较于传统材料更优异的电学、光学、磁学等特性,在自旋电子学、光电器件、场效应晶体管等领域有广泛应用[10,21,22].另外,随着微纳尺度加工设备与测量技术的发展,研究者发展了多种基于二维材料热电性能测试的技术,对其本征优异热电特性进行精准表征.本文中,首先介绍了热电性能中各个物理量的测量方法,并对一些测量方法的局限性进行讨论.随后介绍了石墨烯、过渡金属硫化物、黑磷等不同二维材料的热电输运特性.最后,总结了提升二维材料热电性能的策略与面临挑战,以及对二维材料在热电转化领域中未来潜在应用做出展望.

2 热电性能的测量原理

对于二维材料的热电性质的测量,可以从热电优值的公式Z T=S2σT/κ出发,了解每个参量的测量方法.

2.1 基于场效应晶体管热电特性的测量方法

塞贝克系数为当在材料上施加一个温度梯度时,材料两端会产生一个温度差(ΔT),由于温差带来电子的热运动,材料两端会产生一个热电压(VTEP),即定义塞贝克系数S=-VTEP/ΔT.因此,为了测量塞贝克系数,需要测量材料的温度差和相伴产生的热电压.

图2(a)为研究者利用场效应晶体管测量二维半导体材料塞贝克系数示意图[23,24],其中单层或少层的样品可以通过用机械法剥离或者化学气相沉积方法获得,随后经过电子束刻蚀、蒸金等微纳器件加工步骤,制备特定形状的金属电极.该热电器件由四个探测电极和一个微加热电极组成,对微加热电极通入直流电流或交流电流来产生焦耳热,使得材料上产生一个温度差.当微加热电极通入直流电时,考虑因此可通过输入IHT,在14 电极间获得一个VTEP值,但这种方法也引入了一个麻烦,由于只有在热平衡状态下的测量才能达到精准的数值,而直流电产生的焦耳热需要较长的时间才达到热平衡,因此当要改变IHT对塞贝克系数进行连续测量时,需要较长时间达到热平衡[10].若在微加热电极中通入交流电流i=IHTsin(ωt),根据因 此,此时热电压和交流电流的信号有关(但需注意此时2ω信号与热电压有π/2 的相位差),即可利用对2ω信号的测量来导出热电压.利用以上方法,就可以得到塞贝克系数表达式中的VTEP.

借助于金属电阻对温度极其敏感的特性,可以对电极上电阻标定进而获得样品两端的温度变化.如图2(a)所示,通常将器件放置于高真空恒温器中,杜绝空气热噪音以确保精确的温度测试.在进行温度测试时,利用1,4 电极作为温度探测电极,以获得温度电阻系数(TCR).由可知,IHT引入会使样品两端产生一个 ΔT,借助于测试电表测得不同温度下1,4 电极上电阻随微加热器电流的变化图像R-IHT,并从中得出在某一IHT下电极的 ΔR,由此,利用公式 ΔT=可以计算出1,4 电极上的升温分别为 ΔT1,ΔT2,进而可计算出样品由微加热器加热产生的温度差 ΔT=ΔT1-ΔT2[10,28].至此,可以得出热电压和温度差,即可算出塞贝克系数的大小.

图2 (a) 基于场效应晶体管对二维半导体热电性质测量器件示意图[24];(b) 利用电子双层结构离子液体晶体管对二维材料的热电性质测量器件示意图[25];(c) 悬空热桥法器件示意图[26];(d) 利用H 型方法测量样品的塞贝克系数示意图[27]Fig.2.(a) Schematic image of device for measuring thermoelectric property based on field effect transistor (FET)[24];(b) schematic image of device for thermoelectric property measurement based on electronic double-layer structure ionic liquid transistor[25];(c) schematic image of suspended thermal bridge device[26];(d) schematic image of H-type method device[27].

同时,利用这种方法还可以测量样品的电导率,1—4 电极可以用作四端法测量样品电导率和迁移率[29].四端法由于可以避免接触电阻和肖特基势垒带来的影响,有能力获得更加精确的结果[30].例如,在80 K 温度下,四端法测量的双层MoS2迁移率相比两端法的测量结果提高了1 个数量级,从而实现对样品通道本征性质的测量[28,31-34].并且,该方法可以调节栅极电压的大小,通过调节载流子浓 度n=对材料进行静电掺杂(其中Cox为电介质层的电容,Vg为栅极电压,Vt为阈值电压)[35],可以获得不同载流子浓度下的电导率或塞贝克系数.

在流行的场效应晶体管的基础上,研究者又发展出了电双层结构晶体管[25],如图2(b)所示,电双层结构是在原场效应晶体管的基础上,覆上一层离子液体,为了防止离子液体对金电极产生电化学损伤,在金电极的表面覆盖了一层隔断层.该测量方式与上种方式一致,区别在于调控样品载流子浓度的方法上进行了改变.离子液体场效应掺杂不仅继承了场效应掺杂对样品的清洁性,还可以在更宽的区间调节载流子浓度,可以同时掺杂n 型和p 型载流子,克服了之前只能掺杂单一类型载流子的缺点.

然而,这两种场效应晶体管的方法,都无法测量样品的热导率,因此为了得到样品的热导率和最终的ZT值,需要对样品的热导率进行单独测量,从而引入因样品个体差异的测量误差.常见的热导率测量方法有悬空热桥法、3ω法、拉曼法、电子束自加热法、TDTR 等等[22].本文对二维材料的热导率测量方法进行简单介绍,着重介绍能同时适用于二维材料热导率与电学性质的测试方法,该系列测试方法及原理详见其他综述文章[7,22,36-38].

2.2 悬空热桥法

悬空热桥法在2003 年被Shi 等提出[39],是测量微纳尺度热传导的主要方法之一,它具有着较高的测量精度和适中的操作难度,随着微纳尺度加工技术的不断发展,被越来越广泛地被应用.悬空热桥法由四根悬臂和两个加热电极组成[22,26],如图2(c)所示.它可以同时测量样品的热导率、电导率和塞贝克系数,测试样品可以利用干法转移、湿法转移、pick-up 方法[40-42]等途径转移到热桥器件上.对于热导率的测量,需在悬空电极一端通入一个较大的直流电流产生焦耳热,使样品上产生温度梯度,同时,在两个悬空电极上都通入一个较小的交流电流测量电极电阻的变化,同样利用温度电阻系数(TCR)测量对温度变化进行表征,得到每根电极的温度变化,由此可以获得加热端样品处电极温度变化 ΔTh和热沉端样品处电极温度变化 ΔTs.利用悬空材料热传导模型进行计算[39],即可获得样品热导率:

其中Gb为支撑梁的热导;Gs为样品的热导;Q为由加热电极产生的总焦耳热;L为样品长度;S为样品横截面积.

对于样品塞贝克系数测量,同样需要在一端加热电极通入直流电来使样品产生温度梯度,此时样品会产生热电压,利用样品两端的四根电极测量VTEP,并通过表征温度电阻系数(TCR)获得样品上温升 ΔT,由S=-VTEP/ΔT,即可获得样品的塞贝克系数.然而,由于样品处于悬空状态,无法利用施加栅极电压等方法调控载流子浓度,对塞贝克系数的测量比较受限,因此更经常用作于无法施加栅极电压的纳米线的热电测量.其电导率测量则利用样品两端的四根悬臂电极进行四端法电阻测量.然而,悬空热桥法需要一定大小范围的样品,过短的样品无法搭在悬臂两侧,而过宽的样品会导致加热电极形成的温度梯度不均匀,影响测量的准确性,并且无法施加栅极电压调控也是悬空热桥法测量材料热电性能的缺点之一.转移技术的难度和杂质的引入也限制了该方法的使用,这些都是未来需要解决的问题.

2.3 H 型测量

除了普遍使用的FET 测量方法外,清华大学Wang 等[27],Zhao 与Wang[43]以 及Wang 等[44],提出了H 型热电测量方法,如图2(d)所示.H 型测量方法有着高的电测量精度、可选择激光进行加热、相对简单的实验原理和操作等优点,且满足热导率、电导率、塞贝克系数同时测量,因此其同样可以避免不同样品的个体差异所带来的误差.

如图2(d),H 型测量方式在对电导率的测量时,在电极3,4 通入电流,电极1,2 测量样品两端的电压,即可利用四端法获得样品的电导率.而利用此器件测量塞贝克系数时则需要在一端电极通入电流加热,从而使样品获得温度差 ΔT,由于塞贝克效应,此时会在样品两端产生热电压并由电极2,3 测得,并借助于电极电阻温度系数TCR 的表征,得到样品两端的平均升温,即可算出样品两端的温度差 ΔT与塞贝克系数S=-VTEP/ΔT(与悬空热桥法相似).同时,H 型方法还可测量热导率,样品两端的电极用作为微加热器和微温度探测器,用同样的方式利用金属的电阻和温度之间的关系,表征样品两端金属电极的平均升温,进而得到样品两端的温度差和样品的热导率.这种同时对二维材料热导率、电导率、塞贝克系数的测量极大地避免了由于样品个体差异所带来的误差,但H 型测量器件同时也有着很高的器件刻蚀精度要求和制备难度的要求.

3 二维层状材料

相对于体块材料,二维材料有多种新奇的物理性质.通常,二维材料具备较高的塞贝克系数和电导率,同时具有厚度效应、量子限制效应和极强的各向异性的热导率,例如,晶格结构和化学键的特点导致其面外方向热导率极低而面内方向热导率较高.二维绝缘体材料由于其较差的电性能,不适合用于热电转化,而金属材料又由于费米能级深入能带中,导致有着极低塞贝克系数,这都是对热电性能不利的[45].因此对于二维热电材料的研究,大多数都集中于半导体材料.由Goldsmid—Sharp 可知,可以从禁带宽度预测材料塞贝克最大值[46,47],Smax=Eg/(2eTmax),其中Eg为禁带宽度、Tmax为Smax出现时的温度.由于宽带隙半导体很难达到高掺杂,通常相对窄带隙的半导体有着更加优秀的热电性能.自从石墨烯被解离出来后,新的解离技术也在不断发展,其他由范德瓦耳斯键构成的层间材料也逐渐得到人们关注,典型的如黑磷、二硫化钼等,都具有十分优异的物理性质.这里,我们重点介绍了当前已经报道的石墨烯、黑磷、过渡金属硫化物等二维材料的热电研究进展及为提升热电性能所使用的策略.

3.1 石墨烯

石墨烯是具有单原子层厚度的二维材料,具有蜂窝状晶格结构,自被发现以来就因其有着优异的机械[21,48]、光学[49]、电学[50-53]和热学[54]等性质而被广泛关注.区别于体块石墨的碳原子的sp3杂化,石墨烯层内碳原子为sp2杂化,这导致其有着很强的面内共价键,而层间则通过范德瓦耳斯键相连[55].这些面内sp2杂化共价键也使石墨烯有着极高的热导率(迄今热导率最高的材料),2008 年Balandin课题组[56,57]首次使用拉曼法测量了悬空石墨烯的热导率为5000 W/(m·K)左右,引起了巨大的关注,虽然后续的研究发现其奇高热导率的出现是由于激光吸收率的估计过高导致的,实际热导率在2000—3000 W/(m·K)[54,58],但这并不影响其超高热导率的特性.在石墨烯中,热量主要通过声学声子传输,其声学声子模式由面内声学纵波(LA)、面内声学横波(TA),以及面外声学横波(ZA)组成,如图3(a),研究发现其ZA 声子模式对热传输的贡献高达70%[59].并且石墨烯还具有着极其优秀的电学性质,其理论上能带隙为0,这导致它可以通过掺杂而体现双极性的传输行为,有利于人们进一步探索电传输的内在物理.对于其塞贝克系数,实验和计算上已经证明,通过使用调节载流子浓度的方法,使载流子浓度下降,进而可以得到一个可以媲美体块半导体塞贝克系数的值[15,60-65],因此石墨烯有着非常高的功率因数.然而,石墨烯虽然有着非常优异的电学性能(相对较高的PF),由于其极高的热导率存在,制约了其热电转化特性.

因此,研究者提出了很多方法来抑制石墨烯极高的热导率.例如,由于石墨烯的热导率绝大部分由ZA 声子模式贡献,因此通过抑制ZA 声子模式的传输或增加ZA 声子的散射,即可大幅度降低石墨烯的热导率,2011 年,Seol 等[66]测量了在SiO2上的石墨烯热导率,发现其在室温下,热导率下降到了500—600 W/(m·K),与悬空石墨烯或石墨烯本征热导率相比,下降至其1/6—1/5.这主要是因为ZA 模式声子与基底发生相互作用,导致ZA 声子对热导率贡献发生极大抑制,从而导致越薄的样品出现越低热导率的现象[67,68],与悬空石墨烯的趋势完全相反[69].同理,Thong 等[70]利用悬空热桥法和干法转移技术测量了金纳米粒子沉积的三层石墨烯的热导率,金纳米粒子的存在极大地抑制了其ZA 声子模式,导致了热导率发生80%的下降.除了通过基底和厚度的作用进行调节,在2013 年,Xu 等[58]研究了单层悬空石墨烯热导率随样品长度的变化关系,发现由于石墨烯横向声子平均自由程在10 µm 左右,随着样品长度不断减小,会导致声子散射的增加,热导率会不断降低到500 W/(m·K)以下.如图3(b)是一系列石墨烯热导率与样品长度关系的汇总[38].虽然利用上述方法对石墨烯热导率进行了抑制,但这离理想热电的数值还相差较大,因此进一步降低石墨烯热导率仍是未来研究的方向之一.还有很多方法可以降低石墨烯热导率进而提升其热电性能,这里就不再一一介绍,有兴趣的读者可以关注石墨烯热传导的一些综述文章[22,36-38].

图3 (a) 石墨烯中不同声子模式对热导率的贡献[59];(b) 石墨烯热导率与样品长度关系的不同结果汇总[38];(c) 石墨烯的电导率和塞贝克系数随栅极电压的变化关系(上方插图为石墨烯器件的扫描电子显微镜图像,下方插图为 Vg=—5,—30 V 时塞贝克系数随温度的变化)[15];(d) 在290 K 下,G/hBN 和G/SiO2 的PFT 随栅极电压的变化关系[10]Fig.3.(a) Contribution of different phonon modes to thermal conductivity in graphene[59];(b) summary of thermal conductivity of graphene as a function of sample length[38];(c) conductivity and Seebeck coefficient of graphene as a function of gate voltage(Upper inset: SEM image of a graphene device,the scale bar is 2 µm.Lower inset: Seebeck coefficient of graphene as a function of temperature at Vg=—5,—30 V) [15];(d) PFT as a function of gate voltage in both devices at 290 K[10].

石墨烯电学性能也十分突出,具有着高的电导率和塞贝克系数,且其可以在n 型和p 型区域内都有着很高的功率因数,方便研究者通过掺杂的方式在两个区域对其进行研究.2009 年,研究者首次利用场效应晶体管的方法同时测量了其塞贝克系数和电导率[15,60,61],如图3(c)所示.随着Vg的增加带来载流子浓度不断上升,电导率因此会迅速增加,而塞贝克系数呈现一种先上升再下降的趋势,这是因为在Vg=0 附近的两个极大值之间电子和空穴同时存在,而由于电子和空穴对塞贝克的贡献相互抵消,导致图中情况的出现.随着Vg进一步提高,费米能级进一步深入能带中,导致态密度不对称性的下降,塞贝克系数开始发生下降.2010 年,Dean 等[71]利用h-BN 作为基底,研究了石墨烯电导率与温度和栅极电压Vg之间的关系.h-BN 有着与石墨烯同样的晶格结构,且没有悬空键和电子陷阱的存在,导致其有着原子级光滑的表面.因此使用h-BN 作为基底,可以极大地消除来自SiO2基底带电表面态和杂质[72-75]、表面粗糙程度[76-78]或表面光学声子[73,79]引起的散射,从而使得其载流子迁移率提高了3 倍.这也导致了电导率的极大提升,并通过退火处理,进一步提高了石墨烯的电导率近2—3 倍.2016 年,Duan 等[80]进一步研究了在h-BN 上的石墨烯的热电性质.研究发现,在h-BN 上高质量石墨烯的塞贝克系数最大值比SiO2基底上的石墨烯提升了73 µV/K(分别为182 和109 µV/K),因此其 PFT (功率因数乘以绝对温度)从G/SiO2的峰值6.16 W/(m·K)提升至G/h-BN 的峰值10.35 W/(m·K),提升了接近2 倍,如图3(d)所示.然而,由于石墨烯的高热导率(由于热量的传输过快,无法在材料两端形成稳定的温度差),即使功率因数极高,它的热电优值仍然很低,因此并不适用于普遍的热电应用中.因此,找到一种有效降低石墨烯热导率而不影响其功率因数的方法,这可能是石墨烯热电应用发展的未来方向.同时,石墨烯也有希望应用于热电制冷中[81,82],热电制冷既需要高的功率因数来达到主动制冷的效果,也需要高的热导率达到被动制冷的功效,因此石墨烯有着高热导率的同时,找到更进一步提升功率因数的方法,是其发展热电制冷的一种可能.

3.2 过渡金属硫化物(TMDCs)

过渡金属硫化物是一系列非常重要的材料,具有MX2的通式,其中M代表过渡金属元素,X代表硫族元素.它们的单层结构与石墨烯和h-BN 不同,是三层原子厚度的“三明治”结构[83],其中过渡金属元素被硫族元素夹在中间,如图4(a)所示[84].层间作用与石墨烯一致,由范德瓦耳斯力相连,因此可以利用机械剥离方法解离出薄层甚至单层的样品.过渡金属硫化物有着优异的化学稳定性、机械性能[85-87]、可控的带隙和优良的电学性质,在光电[88,89]、压电[90,91]、谷电子学[92,93]等方面有着巨大应用潜力,而其热导率比石墨烯低1—2 个数量级,这使得它们在热电领域有着巨大应用潜力.

MoS2是过渡金属硫化物中最为广泛关注半导体材料,有着相对石墨烯低1—2 个数量级的热导率,理论计算表明[94],MoS2有着较低的群速度和较大的格林爱森常数,这导致其平均自由程仅有14.6 nm,根据公式κ=1/3CLvl(其中C L为晶格热容,v为声子群速度,l为声子平均自由程),其热导率相对较低[95],实验测量值从20 到140 W/(m·K)不等[95-98],这主要是源于不同测试方法和不同制备过程带来的样品质量差异,如图4(b)总结了MoS2热导率的部分实验和计算的结果[38].Gu 等[99]利用玻尔兹曼传输方程计算、Xu 等[100]利用非平衡分子动力学模拟发现其从1 到3 层热导率有着明显减小,这可能是由于声子色散和厚度依赖的非简谐性导致的,这种相对较低的热导率适合于热电应用的研究.关于MoS2热输运更多的性质,有兴趣的读者可以阅读相关综述文章[22,37,101].

MoS2是典型的半导体材料,它有着可控的能带隙,随着层数的降低(从块体到单层),MoS2有着间接能带隙(1.2 eV)到直接能带隙(1.8 eV)的转变[83,102],并且通过调控栅极电压,其有着半导体态至金属态的转变[103].2016 年,Kayyalha 等[28]研究了SiO2基底上的MoS2随层数变化的热电性能,如图4(c)所示,发现由于电子平均自由程的能量依赖关系、增加的有效载流子体密度和更大的谷简并度和有效质量的出现,MoS2的电导率最大值出现在双层,而由于态密度不对称性提高,塞贝克系数在4 层时达到最大,并发现了MoS2金属相到半导体相的相变,这使MoS2在双层时有一个最大的功率因数,如图4(d)所示.另外,在2 层以上,电导率和功率因数对层数有着明显的依赖关系,而塞贝克系数对层数的变化并不敏感,因此可利用层数的调节去改善能带结构进而去改善热电性能.同样,Hippalgaonkar 等[35]研究了不同厚度的MoS2的热电性质,其在一个高载流子浓度下(n=1.06 ×1013cm—2)同样发现双层MoS2有着最高的功率因数S2σ=8.5 mW/(m·K),图4(e)所示.Cai 等[104]通过工程界面键合畸变设计了一种几乎没有肖特基势垒的电接触策略,使MoS2FET 中接触电阻达90 Ω·µm(接近量子极限),WSe2中迁移率高达358000 cm2/(V·s),这极大地提升了TMDCs 的电性能.二维材料MoS2也因此在热电方面相对于体块有更大的潜力[105].这里对其热电性质做出简略介绍,在后面的章节中会对二维TMDCs 热电性能的提升做出详细介绍.因此,相对于石墨烯的高热导率,有着更低的热导率且电学性质优异的二维MoS2在热电应用中有着巨大潜力.

图4 (a) 单层二硫化钼的示意图(其中紫色为Mo 原子、黄色为S 原子)[84];(b) 室温下关于MoS2 的热导率研究结果的汇总[38];(c) 不同 Vg-Vth 下,四端法测得的MoS2 的电导率和塞贝克系数随样品厚度(层数)的变化关系[28];(d) 不同 Vg-Vth 下,MoS2 的功率因数随样品厚度(层数)的变化关系[28];(e) 不同厚度(1—3 层)的MoS2 的功率因数随 V g 的变化关系[35]Fig.4.(a) Schematic image of monolayer MoS2 (Where purple is Mo atom and yellow is S atom) [84];(b) summary of thermal conductivity of MoS2 at room temperature[38];(c) four-probe conductivity and Seebeck coefficient of MoS2 as a function of the thickness (number of layers) measured at different Vg-Vth values;(d) PF of MoS2 as a function of the thickness (number of layers)measured at different Vg-Vth values[28];(e) PF of MoS2 with different thick (monolayer-three layers) as a function of the Vg [35].

其他过渡金属硫化物在热电领域也有着巨大的潜力,理论计算和实验都证明,由于过渡金属硫化物的热传输性能可利用硫族元素进行调节[109,110],硫族元素从S 到Se 的变化会使热导率下降,这会更加有益于热电应用.理论上也对部分过渡金属硫化物的ZT值进行了预测[111],其中过渡金属硫化物通常有着极高的热电应用潜力,且低维材料相比体块在热电方面有着巨大的发展前景.对于WSe2来说,Yoshida 等[106]利用电子双层结构场效应晶体管离子液体掺杂的方法研究了WSe2的热电性能,如图5(a),发现其展现着双极性的传输行为,且在n 型和p 型传导区域分别有着32 µV/(cm·K2)和37 µV/(cm·K2)的功率因数,它有着与著名热电材料Bi2Te3可比拟的功率因数和比MoS2更低的热导率,使得它有着巨大的热电潜力.同样,TiS2也有着非常好的电学性能,在室温下塞贝克系数达到—251 mV/K,因此有着一个37.1 mV/(cm·K2)的功率因数[112],然而它也有着一个相对较大的68.1 mW/(cm·K)的晶格热导率,因此未来可以通过进一步降低其晶格热导率来提高它的热电性能.对于PdSe2,理论预测发现其最高有着ZT=1.1 的极高的热电优值[113].2017 年,Oyedele 等[114]首次制备并解离出少层的PdSe2晶体,发现PdSe2有着各向异性的传输性能和极强的空气稳定性,并利用拉曼光谱和FET 等手段对其做了深入的表征,发现其有着双极性的电传输行为和金属至半导体电传输行为的转变,该系列结果为之后的研究做出了十分重要的贡献.2020 年,Zhao 等[107]首次测量了具有特殊晶格结构的PdSe2的热电性质,如图5(b)所示,发现其有着优异的双极性传输行为和极高的迁移率,并且由于其随着层数的降低会出现能带简并度的增加和量子限制效应,因此可以提高功率因数(5 nm 厚PdSe2高达1.5 mW/(m·K2)),并且由于其褶皱的五角晶格结构导致其有着极低的热导率[115],这极其有利于热电应用的需求,其特殊的晶格结构导致其层间耦合异常强烈,因此给予我们可通过层数的调控进而调控其热电性质的途径.同样,2022 年也有研究者利用DFT 和玻尔兹曼理论计算了单层PdSe2在中高温度下的热电性能[116],并讨论了应力对其的影响,理论计算表明,PdSe2虽然可以承受较大的拉伸应力,而在压缩应力下却出现结构不稳定,2%的拉伸应力使得其ZT值出现急剧的下降(超过50%).除此之外,少层InSe 也被实验和理论证明有着优异的热电性能[108,117-119],如图5(c)所示样品厚度和热德布罗意波长之间的关系,研究者发现由于量子限制效应,7 nm 厚的InSe 的塞贝克系数可以达到高于体块的570 µV/K,因此有着更高的功率因数.由此,具有巨大的热电应用潜力的TMDCs 材料等待着我们进一步挖掘和探索.

图5 (a) 300 K 下,极薄单晶WSe2 的电导率(两端法)、塞贝克系数和功率因数随 Vg 的变化关系[106];(b) 厚度为5 和9 nm 的PdSe2 薄片的功率因数[107];(c) 室温下不同厚度的InSe 薄膜的功率因数随载流子浓度的变化关系[108]Fig.5.(a) σ2D,S and S 2σ of ultrathin WSe2 single crystals as a function of the Vg at T=300 K[106];(b) power factor of PdSe2 flakes with thickness of 5 and 9 nm[107];(c) power factor of InSe film with different thickness as a function of carrier concentration at room temperature[108].

3.3 黑 磷

黑磷作为一种二维半导体材料,有着厚度可控的能带带隙,理论计算表明,体块有着0.3 eV 的直接带隙,单层黑磷则有着2 eV 的直接带隙[120],并且,黑磷有着极其褶皱的晶格结构且有着强烈的面内各向异性,分为ZZ方向和AC方向,如图6(a)所示.黑磷与石墨烯等材料一致,面间由范德瓦耳斯键相连,借助于机械解离可获得少层样品.但由于黑磷极易氧化,导致其不能在空气中长时间暴露,也阻碍了人们对它的研究[121-124].

图6 (a) 黑磷晶体结构的示意图[125];(b) 黑磷纳米带在AC 和ZZ 方向的热导率和杨氏模量测量值,其中热导率和杨氏模量有着相似的各向异性比值(分别为2.24 和2.05)[126];(c) AC 方向和ZZ 方向的黑磷纳米带电导率(c)和塞贝克系数(d)随温度的变化关系[127];(e) 黑磷塞贝克系数的少层实验数据和体块理论计算数值(实线为 S x,虚线为 S y)的比较[25];(f) 210 K 下,少层黑磷的功率因数随栅极电压的变化关系[25]Fig.6.(a) Schematic image of BP reproduced with permission[125];(b) thermal conductivity and Young’s modulus values of the BP nanoribbons.The thermal conductivity anisotropy ratio (≈2.24) between ZZ and AC is similar to that of Young’s modulus (≈2.05)[126];temperature dependence of electrical conductivity (c) and Seebeck coefficient (d) of BP nanoribbons along the AC and ZZ directions[127];(e) comparison between experimental data and bulk values of theoretical calculation (S x,solid line;S y dashed line) of Seebeck coefficient of BP[25];(f) power factor of few layer BP as a function of gate voltage at 210 K[25].

黑磷在AC方向存在极其褶皱的长城状结构,导致其有着极强的非简谐性,AC方向因此有着更低的群速度和声子弛豫时间、较低的热导率[125,128].理论计算预测,由于非简谐性散射的作用,其ZZ方向与AC方向的热导率比值高达2.2[129].2015 年,Lee 等[125]制备了ZZ与AC两种晶格方向纳米线,并用悬空热桥法对其两个方向的热导率随厚度的关系进行了测量,其热导率各向异性的比值室温下与厚度无关(维持在2 左右),符合理论预测.随着厚度从300 nm 降 至50 nm,ZZ方向热导率从27 W/(m·K)降至12 W/(m·K),而AC方向热导率最低达到5 W/(m·K),这极其低的热导率有助于热电性能提升.2018 年Zhao 等[126]利用电子束加热法对不同方向的黑磷纳米线进行了测量,如图6(b)所示,发现其各向异性的比值与杨氏模量的比值近乎一致,可以认为黑磷中的各向异性行为是由声子群速度的各向异性引起的.这种由于非简谐性散射导致的声子群速度的降低极大地抑制了热量的传输,从而同样出现了低于5 W/(m·K)的极低的热导率[130].黑磷的电学性能的各向异性恰好与热传输性能相反,如图6(c)和图6(d)所示[127],在热导率更低的AC方向恰好出现了更高的电导率和塞贝克系数,这种在同一方向出现的电学性能更好而热学性能更低的性质,恰好满足了追求高热电优值的需求.实验结果表明,少层黑磷有着比体块黑磷更大的塞贝克系数,分别为510 µV/K 和335 µV/K[25,131].通过第一性原理和玻尔兹曼传输理论计算也证明其有着优秀的热电性能,Zhang 等[132]发现在1.5 × 1020cm—3的浓度下有着1.1 的热电优值.Saito 等[25]利用离子液体晶体管方法对二维层状黑磷进行了更大载流子范围且清洁的掺杂,如图6(e)和图6(f)所示,得到了相对体块黑磷更大的塞贝克系数(0.51 mV/K),并且其功率因数在V g=0.7 V 时达到了460 µW/(m·K2),但仍比理论预测的数值[133]要小很多.当然也有众多研究者通过利用应力、掺杂等方法进一步提升了黑磷的热电性能,将会在接下来的章节进行介绍.但由于本征黑磷极易氧化,大部分对它的探索在于理论研究.对于黑磷的进一步实验研究仍是挑战,所以对黑磷热电性质实验上的进一步挖掘仍是未来可以发展的方向.

3.4 其他二维材料在热电方面的应用

除了广泛研究的石墨烯、过渡金属硫化物、黑磷等,还有很多其他二维材料被发现同样有着优异的热电性能.例如地球环境丰富的SnSe,它有着稳定的化学性质和层状正交晶格结构[134,135],与黑磷结构相似,但Sn 和Se 两种元素分别占据不同位置.因此,其同样有着强烈的各向异性和非简谐性,这体现为极大的格林爱森常数,导致其拥有极低的热导率而有利于热电方面的应用.Ding 等[136]利用第一性原理计算预测了单层SnSe 的热电性质,发现AC方向由于更强的非简谐散射存在,其有着比ZZ方向更低的晶格热导率,并且在高于600 K时其有着低于1 W/(m·K)的极低热导率,这可能源于高温下声子平均自由程的减小(＜2 nm)[137],然而面内的电导率和塞贝克系数随温度变化不大,这导致在高温下单层SnSe 有着很好的热电传输性能.与体块材料相比,研究者发现在单层SnSe 中,由于层间范德瓦耳斯相互作用消失,其面内声子热传导能力发生增强[138,139],这其实一定程度上降低了SnSe 的热电性能(单层ZT=0.9,体块ZT=2.6).同时,Sun 等[140]通过考虑电声耦合的影响计算了单层热电材料SnSe 的热导率,发现载流子密度超过1013cm—2时(载流子浓度超过1020cm—3),单层SnSe 的热导率下降了30%(而这种载流子浓度是热电应用中常见的),因此认为能够通过载流子的掺杂达到更好的热电性质.

此外,二维铁电材料Bi2O2Se 晶体由于其稳定的化学性质、优异的电学性能[142-145]及铁电软声子模式导致的低热导率[146]也成为潜在热电材料的候选者.Yang 等[24]实验上研究了少层Bi2O2Se 晶体的热电性质,发现随温度的降低,载流子散射机制从极性光学声子散射[147,148]转变为压电散射[149-151],这导致了迁移率的持续增加(超过3100 cm2/(V·s)),并且发现散射机制的转变温度可以通过栅极电压进行调节,使其可以在很宽的温度范围内维持超高的迁移率,从而提升电导率而不影响塞贝克系数,因此在很宽的温度范围内获得了超过400 µW/(m·K2)的功率因数,如图7(a)所示.同样有着极大格林爱森常数的GeAs2晶体也被预测有着极好的热电潜力[141],GeAs2具有褶皱的层状结构,层内由共价键相连,层间作用键为准共价键和范德瓦耳斯键,这导致其有着很强的各向异性和非简谐作用,室温下沿着褶皱方向的面内热导率为0.68 W/(m·K),其也有着厚度可控的能带隙,从体块变为单层,其能带隙由0.99 eV 的间接带隙变化为1.64 eV 间接带隙,这导致其有着大的开关比,并且由于其能带的简并导致其有着高的塞贝克系数[152]和适中的迁移率[153],这使其有着和石墨烯相似的功率因数,进而有着很好的热电性能(如图7(b),900 K 下n 型GeAs2热电优值ZT=2.1 而p 型GeAs2热电优值ZT=1.8).实验上,Li 等[154]利用机械剥离的方法解离出少层的GeAs2,并测量了其光学和电学性质的各向异性,发现其电导各向异性比为1.8,与黑磷各向异性接近.后来研究揭示了GeAs2层间除了范德瓦耳斯键以外还有准共价键的作用,这使其很难解离出少层的GeAs2.因此对于GeAs2热电性质的研究主要集中于理论计算,新的解离方法,例如金辅助解离法[155-158],可能是其未来发展的方向.

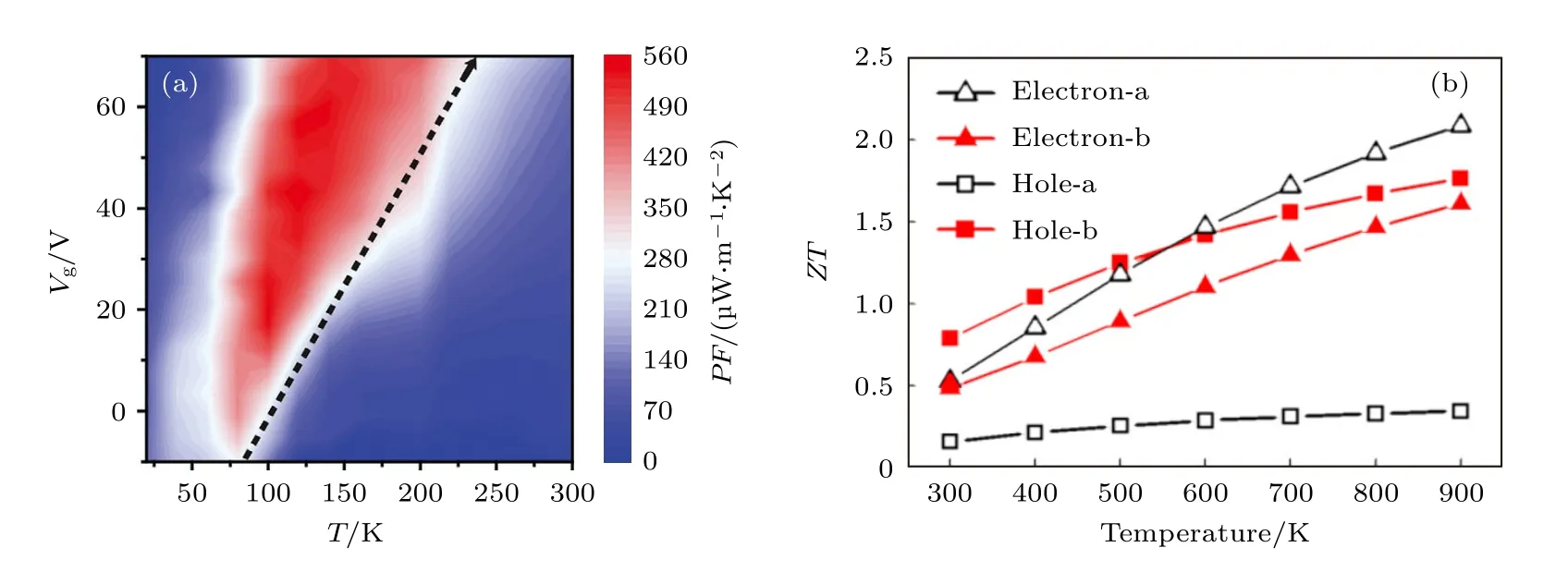
图7 (a) 少层Bi2O2Se 晶体的功率因数随着栅极电压和温度的变化关系[24];(b) 单层GeAs2(n 型或p 型)在不同温度下的热电优值的最大值[141]Fig.7.(a) PF of few-layer Bi2O2Se as a function of gate voltage and temperature[24];(b) maximum ZT of monolayer GeAs2 at different temperature (including n type and p type)[141].

4 热电性能提升方法

为了提升热电传输性能,研究者往往需要提高功率因数或降低热导率,通常使用的方法如利用纳米结构工程降低二维材料的热导率或利用能带工程增加或优化功率因数.例如,二维材料有着极高的表面-体积比,这导致其能实现高效的表面化学功能化[82,159].二维材料也极易受缺陷、杂质等影响,因此可以通过掺杂或缺陷工程有效地调节其热电性能[101,160].这里对目前已报道的基于二维材料热电传输性能的提升策略进行详细介绍.

4.1 缺陷工程

考虑二维材料具有原子级厚度而具有巨大比表面积,缺陷的存在对二维材料的性能影响要远大于体块材料.常见的缺陷包括空位、间隙原子、替代原子等等,二维材料中缺陷的形成能增强声子的非简谐性散射,它不仅能使晶格热导率发生降低,还能在一定程度上调节电传输性能进而达到提升热电性能的目的[98,161-163].例如,可以通过缺陷的引入进一步降低二维MoS2的热导率而提升热电性能,2018 年,Aiyiti 等[164]通过利用氧离子轰击方法,在悬空少层MoS2产生空位,发现随着空位浓度的增加导致了非简谐散射增强,其热导率发生明显下降.2021 年,Zhao 等[163]利用He+辐射配合理论计算研究了MoS2中Mo 原子空位和S 原子空位对热导率的影响,从实验上验证了Mo 空位的存在比S 空位对于热导率有着更大的削弱作用,这有助于其热电性质的进一步调控.在二维材料的制备过程中,也不可避免会产生一些缺陷(空位、替代杂质等等),这些缺陷态的形成会影响载流子的激发和迁移率,Sharma 等[160]计算了空位(S 空位、Mo 空位、MoS 空位、MoS2空位)对单层MoS2热电性质的影响,并发现随空位缺陷的产生,单层MoS2有着可调的能带隙,并且在室温下发现具有S 空位和MoS2空位的样品ZT值分别达到6.24和1.3.2020 年Wu 等[159]实验上报道了具有S 空位缺陷的六层MoS2异质结构有着异常强的热电性能,其发现S 空位的存在引入了类磁性杂质和能带杂化,这导致近藤效应的出现[165],因此在低温下观察到了极大的电导率和反常的正塞贝克系数(高达2 mV/K),这也导致了其功率因数有着2 个数量级的增加,如图8(a)和图8(b).研究者也在MoS2/SiO2系统中证实了声子拖曳效应存在[166,167],其有效提高了塞贝克系数.对于GeAs2,理论计算预言其有着极强热电性能,Ge 空位的存在,不仅降低了其热导率,还可以使GeAs2的能带隙明显减小并显示出金属性的传输行为[168],达到热电传输性能增强的效果.另外研究者发现,在石墨烯中通过掺杂硅引入缺陷,导致其热导率出现2 个数量级的下降,而电学传输性能仅仅出现了3 倍的减小,使得其热电优值有了明显的提升[169].Wu 等[170]研究了同位素杂质对热导率的影响,发现对于MoS2,Mo 同位素有着比S 同位素更加明显的降低热导率的作用,由于Mo 同位素质量较大,会更多影响低频声子,而热传导主要由声学声子(低频)来实现的.此外,实验上通过氦离子辐射引入本征缺陷成功地解耦了Bi2Te3中塞贝克系数和电导率之间的关系[45],使塞贝克系数和电导率同时得到了提升.通过霍尔效应的测量发现,引入的本征缺陷具有类似供体的作用,使载流子浓度不断上升,增强了样品的电导率.同时,根据弛豫时间模型,塞贝克系数在简并掺杂极限下为

图8 (a) MoS2/hBN 器件的四端法电导率随温度和栅极电压的变化关系(低温下电导率出现异常的峰值用红色虚线标出)[159];(b) MoS2/SiO2 和MoS2/hBN 器件的塞贝克系数与温度的变化关系(其中MoS2/hBN 器件 Vg=70 V 以圆形表示,V g=50 V 以方形表示,Vg=30 V 以钻石形状表示)[159];(c) 氦离子辐射同时增加Bi2Te3 塞贝克系数和载流子浓度(虚线为不同散射弛豫时间指数下塞贝克系数的计算结果)[45];(d) 不同厚度的Bi2Te3 的功率因数随辐射剂量的变化关系[45]Fig.8.(a) Four-probe electrical conductivity of MoS2/hBN devices as a function of Temperature and back gate voltage[159];(b) temperature dependent Seebeck coefficient of MoS2/SiO2 and MoS2/hBN device at Vg=70 V (circle),50 V (square),and 30 V (diamond) [159];(c) the simultaneous increase of Seebeck coefficient and carrier concentration of helium ion irradiated Bi2Te3[45];(d) irradiation dose dependent power factor of Bi2Te3 with different thicknesses[45].

其中εF为费米能级,间接地描述了载流子浓度的变化;r为电子弛豫时间与动能关系指数(τ(ε)∝εr),其中当声学声子散射主导时r=—1/2,光学声子散射主导时r=1/2,离子杂质散射主导时r=3/2[171],因此该公式反映了塞贝克系数与载流子浓度和散射机制之间的关系.随着辐射浓度的提升,其散射机制发生了由声学声子散射到离子杂质散射之间的转变,因此其解耦并同时提升了样品的电导率和塞贝克系数,如图8(c)和图8(d),通过引入的掺杂进一步降低了Bi2Te3热导率,使三个热电关键参数同时向预期方向发生了改变,从而极大地提升了Bi2Te3的热电性能.

4.2 掺杂作用

相比空位等缺陷对晶格热导率的影响,元素掺杂不仅能降低热导率,还能够对能带进行调节,并改变载流子输运特性.例如,Guo 等[172]测量了金修饰的MoS2的热电性质,由于金纳米粒子的修饰作用,2H 相的MoS2得到p 型掺杂,而且掺杂载流子在界面局部弯曲带附近注入能量滤波,使得电导率和塞贝克系数同时增大.类似地,Ng 等[173]利用退火方法研究了Li 掺杂LixMoS2的热电性能,借助于退火处理,LixMoS2由1T′/2H 的混合相转变为2H 相,这种由半金属相到半导体相的转变,极大地提升了体系塞贝克系数和功率因数,如图9(a)和图9(b)所示,该方法提供了一种通过改变MoS2相结构来提升热电性质的实验策略.同样的,研究者也利用金纳米粒子对黑磷进行了掺杂,通过提高载流子浓度极大地提升了其电导率,而黑磷的塞贝克系数只得到了轻微的降低,使功率因数得到明显的提升[174],并能够使黑磷的易氧化的特性减弱.Zhang 等[132]通过计算发现由于Sb 的掺杂(P0.75Sb0.25),少层黑磷的ZT 值达到6.0.研究者也探究了Cs2CO3和MoO3对黑磷原位掺杂的影响[175],发现Cs2CO3和MoO3的原位掺杂会对黑磷分别进行n 型和p 型掺杂,能够有效地提高载流子浓度和迁移率并降低肖特基势垒,为提升热电性能提供了一种新途径.2017 年,Kong 等[176]研究了氧掺杂的MoS2热电特性,氧原子的加入会在本征MoS2中混入高导电性的MoO2态,使得其在室温下具有极低的热导率(3.1 W/(m·K)),同时具有较高的电导率和塞贝克系数,从而极大地提升了热电优值,如图9(c)和图9(d)所示.同样为了增强二维材料的电学性能,Perera 等[177]利用离子液体晶体管的方法,对MoS2进行更大载流子范围掺杂,进而提升载流子浓度,并通过改善肖特基势垒降低了接触电阻,使其迁移率增加到60 cm2/(V·s).因此选择一个适合提升热电性能的掺杂方法,不仅能通过增强的非谐性作用来降低声子热导率,还能提升材料的电输运性能,从而进一步提升其热电转化性质.

图9 (a) 在SiO2/Si 基底上,真空退火3 次LixMoS2 的拉曼光谱图[173];(b) 经过每次退火后的LixMoS2 的塞贝克系数、电导率和功率因数[173];(c) 沿各个方向的本征MoS2 和氧原子掺杂MoS2 的PF 随温度的变化[176];(d) 沿各个方向的本征MoS2 和氧原子掺杂MoS2 的热导率随温度的变化[176]Fig.9.(a) Raman spectra of a LixMoS2 flake on SiO2/Si substrate across three separate annealing cycles performed in vacuum[173];(b) Seebeck coefficient,electrical conductivity,and power factor of LixMoS2 device across all annealing cycles[173];(c) power factor of the pristine MoS2 and oxygen-doped MoS2 along both directions[176];(d) thermal conductivity of the pristine MoS2 and oxygendoped MoS2 along both directions[176].

4.3 超晶格结构

超晶格结构的构建对热电性质也有着巨大的影响,通常通过制备超晶格结构,不仅能调节材料的能带结构,还能极大地抑制声子传输.2006 年Böttner 等[178],Venkatasubramanian 等[179]和Harman 等[180,181]对部分薄膜超晶格结构热电材料及其应用进行了总结,发现通过构建超晶格结构使得热电优值ZT值可超过体块材料热电优值的限制,如图10(a) 1996 年,Hicks 与Dresselhaus[6]和Hicks 等[182]研究了PbTe/Pb1—xEuxTe 超晶格的热电性质,随着量子阱厚度的不断变薄,量子限制效应使其S2n值比最佳的体块值提高了4 倍,且与理论预测的趋势十分吻合,另外如果考虑超晶格结构对声子散射作用,其最终的ZT值将会有更大的提升.

最近,一种新的二维纳米结构——横向超晶格结构的发现,吸引了研究者的关注,Ding 等[183]通过第一性原理计算发现,在MoS2和MoSe2组成的横向超晶格结构中,声子发生了强烈的非简谐散射,使得其热导率降低80%,如图10(b).Wan 等[184]利用二维材料TiS2作为主体,利用电化学插入的方法合成了TiS2/有机物的褶皱超晶格结构,如图10(c)和图10(d),其通过层间相互作用提高了声子的非简谐散射,从而极大地降低了其热导率,而由于TiS2层始终主导电子传输,使得其电传输性能(功率因数)损失较少,从而使其相比单晶TiS2的ZT值有明显的提升.2022 年,Wang 等[185]利用同样的电化学还原方法在TaS2层间插入有机物,制备出均匀分布的有机物/TaS2的杂化结构(SCCM-TaS2),其发现在室温下电导率有着2 倍的增加(从3000 S/cm 左右增加到6100 S/cm),而塞贝克系数只有轻微的下降(从—7.6 µV/K 降至—6.6 µV/K),通过霍尔测量发现,这可能是由于载流子浓度的提升导致的,并且研究者还发现由于有机物的插入,导致热导率有着7 倍的降低,这最终导致了SCCM-TaS2的ZT值相比TaS2有着10 倍的增加,这也为未来提升热电性质提供了新途径.Luckyanova 等[186]从实验和理论上通过控制超晶格结构的单层厚度(周期数),系统地研究了不同周期数超晶格结构的热导率随温度的变化关系,发现对于低周期数超晶格结构,由于极强的边界散射作用,极大地湮灭了声学声子,导致热导率发生巨大的降低,这非常有利于热电性能的进一步提升.由此可见,通过设计超晶格结构的方法,不仅能增加声子的界面散射降低热导率,还可以对能带结构进行调节,因此寻找可以降低热导率又能维持甚至增强电子运输的策略,从而进一步提升热电性能,是二维材料热电应用研究的方向.

图10 (a) Bi2Te3/Sb2Te3 超晶格、PbSnSeTe/PbTe 量子点超晶格、PbTe0.02Se0.98/PbTe 量子点超晶格的热电优值[178];(b) 计算获得的不同周期厚度的横向超晶格晶格热导率随温度的关系[183];(c) TiS2[(HA)x(H2O)y(DMSO)z]超晶格材料的HAADF-STEM 图像(展示了褶皱的晶格结构)[10];(d) 放大的TiS2[(HA)x(H2O)y(DMSO)z]超晶格材料的HAADF-STEM 图像[10];(e) 本征TaS2 和SCCM-TaS2 的电导率[185];(f) 本征TaS2 和SCCM-TaS2 的塞贝克系数[185]Fig.10.(a) Thermoelectric figure of merit for Bi2Te3/Sb2Te3 superlattices,PbSnSeTe/PbTe quantum dot superlattices,and PbTe0.02Se0.98/PbTe quantum dot superlattices[178];(b) temperature dependence of calculated lattice thermal conductivity of lateral superlattices with different periodic thicknesses[183];(c) HAADF-STEM (high-angle annular dark field scanning transmission electron microscope) image of the TiS2[(HA)x(H2O)y(DMSO)z] hybrid superlattice showing a wavy structure[10].(d) magnified HAADFSTEM image of TiS2[(HA)x(H2O)y(DMSO)z][10];(e) electrical conductivity of the pristine TaS2 crystals and SCCM-TaS2 hybrid structure[185];(f) seebeck coefficient of the pristine TaS2 crystals and SCCM-TaS2 hybrid structure[185].

4.4 应力工程

除了复杂的缺陷和掺杂的引入,物理方法例如施加应力或增加褶皱也可以调节声子散射并调节能带结构[187-189].实验上对二维材料面内施加应力的方法有很多[190],例如向褶皱粗糙的基底上转移二维材料、利用弯曲柔性的基底制备二维材料、利用基底的热膨胀或冷却和利用AFM 施加应力[191-195]等等,如图11(a)—(c).研究发现,随着拉伸应力的增加,MoS2的热导率出现了线性降低的趋势[196].除了显而易见的应力对声子的软化作用,研究者也发现了应力对能带的调节作用,通过施加应力于单层和双层二硫化钼[197],出现了直接带隙至间接带隙的改变.而与其相反,对WSe2的应力研究发现[198],通过对其施加应力,发生了间接带隙到直接带隙的转变,并在WS2中发现了应力带来的功函数的改变[192],电子能带的优化使得进一步调节材料的热电性质成为可能.如图11(d)所示,借助于第一性原理计算,Hoat 等[199]研究了应力对黑磷热电性质的影响,在压缩应力的作用下,热电优值发生明显的提高,室温下ZT为0.665,ZT最高可达0.95,这可能是谷简并度增加或能带聚合所导致的[200].2019年Bera 和Sahu[201]研究了应力对单层WS2的热电性质的影响,发现对于n 型和p 型的样品,拉伸应力和压缩应力有着不同的影响,随着拉伸应力的增加,p 型WS2由于谷简并度的增加带来了功率因数的显著提升,而对于n 型WS2则会随着压缩应力出现,功率因数出现更强烈的提高,如图11(e).同样,Ng 等[195]借助于表面粗糙的硅片,获得了少层的褶皱MoS2,其发现扭曲的晶格结构可以导致声子-载流子散射的减弱,这使其迁移率突破了声子散射极限值而呈现2 个数量级的增加,且不会导致载流子浓度的增加,这最终使其在室温的低掺杂浓度下(n～3×1018cm—3)获得了极高的功率因数S2σ≥1 mW/(m2·K),如图11(f)所示.通过第一性原理,研究者计算了双轴拉伸应力对单层ZrSe2的热电性质的影响[202],发现由于应力作用使ZrSe2发生了能带聚合并增加了谷简并度,使p 型和n 型的ZrSe2的ZT值分别提高至4.58 和3.84.因此,应力工程不仅可以使声子软化影响其热传输,还能够极大程度地调节能带结构与电学性质,使与热电相关的物理量同时优化,这有助于提升材料的热电转化性能.

图11 (a) 利用AFM 对悬空单层MoS2 施加应力的示意图[85];(b) 褶皱的单层MoS2 的构造过程示意图[193];(c) 利用三点弯曲法对MoS2 进行延伸示意图[194];(d) 黑磷的热电优值随温度和应变的变化关系[199];(e) 在300,600和900 K下施加双向压缩和拉伸应变的n型或p型WS2 的 S2σ τ 值[201];(f) 不同厚度(层数)的平坦和褶皱的MoS2的功率因数随载流子浓度的变化关系[195]Fig.11.(a) Schematic image of inducing strain to the suspended monolayer MoS2 by AFM[85];(b) schematic image of the fabrication process of wrinkled MoS2 nanolayers[193];(c) schematic image of the extension of MoS2 by the three-point bending apparatus[194];(d) ZT of BP as a function of temperature and strain[199];(e) S2σ τ of WS2 with applied both biaxial compressive and tensile strain for n-type and p-type doping at 300,600 and 900 K[201];(f) PF of flat and ripped MoS2 as a function of carrier concentration with different thickness[195].

5 总结与展望

二维材料的出现引起了人们广泛的关注,其新奇且丰富的物理性质使其在很多领域中得到了应用.本文中,总结了近些年来二维材料在热电领域中应用和研究进展,并介绍了常见的热电测量方法.以往的研究报道了很多有效的途径去提升热电性能,除了常见的态密度约束,还可以从缺陷工程、元素掺杂、超晶格结构的构建、肖特基势垒的消除等方法对热电性能进行调控,另外,通过引入近藤效应或不同散射机制,使得调节二维材料的热电性能成为可能,且使热电应用中三个关键的物理量,电导率、塞贝克系数和热导率,进行解耦.二维材料热电性质的研究为研究电子-声子之间的相互作用提供了新平台.二维家族中仍然有许多材料未被发现,对其热电应用的研究有着非常广阔的前景.针对二维材料在热电转化中的应用,本文提出该领域目前存在的瓶颈问题与未来发展的方向.

1) 研究者目前需借助于复杂的半导体器件加工手段构建测试器件,这将会引入更多的缺陷和其他不确定因素,使得测量二维材料本征性质具有挑战性,对于测量技术,适用于二维材料热电性质的商业化技术和方法仍然存在空缺,构建稳定可靠、高测试分辨率的热电测试系统是表征二维材料热电特性的关键.

2) 目前仍然无法大规模制备高质量、高迁移率的二维半导体材料,常见的机械剥离方法虽然可以制备出高质量、高迁移率的样品,但却无法实现大规模制备的需求.而常见的CVD 生长二维半导体材料的方法虽有着极高的制备效率,但却无法达到机械剥离制备样品质量之高.因此一个能够大规模制备高质量、高迁移率的二维半导体材料的方法对热电领域的发展是至关重要,需要被研究者进一步发展.

3) 二维材料由于其特殊层间化学键,导致面外方向热导率极低而面内方向热导率较高,单从这一特点来讲,其面外方向有着更优异的热电性能而面内方向有着更好的热传输性能,因此对二维材料面外方向热电性质的研究同样是十分有意义的.然而目前对二维材料热电性质的研究仍局限于面内方向,对于面外方向的热电性质研究没有较好地开展,找到对其更加精准的测量方法是十分关键的.

4) 二维材料家族非常庞大,对每个材料进行制备甚至表征及测量是非常复杂且困难的,目前研究者开展大量的理论或实验研究来探索优化二维层状材料热电性能,因此需要配合近年来机器学习技术的发展,利用机器学习强大的分析计算能力的特性,寻找出适合热电应用的材料,这将会极大地促进热电领域发展,相信在未来会有更多二维材料在热电领域产生令人兴奋的结果.