基于非高斯态区分探测的往返式离散调制连续变量量子密钥分发方案*

吴晓东 黄端

1) (福建工程学院管理学院,福州 350118)

2) (中南大学计算机学院,长沙 410083)

往返式离散调制连续变量量子密钥分发,无需使用两台独立的激光器也能本地生成本振光,并且信号光与本振光均来自于同一台激光器,在有效保证系统实际安全性的同时,具有较好的同频特性.此外,该方案与高效纠错码具有良好的兼容性,即使在低信噪比情况下也能获得较高的协商效率.然而,基于非可信信源模型的往返式光路结构存在较大的过噪声,严重限制离散调制方案的最大传输距离.针对这个问题,本文提出基于非高斯态区分探测的往返式离散调制连续变量量子密钥分发方案,即在探测端部署非高斯态区分探测器,采用自适应测量方法并结合贝叶斯推论,可以在满足低于标准量子极限错误概率的情况下无条件区分出基于四态离散调制的四种非正交相干态.本文详细分析了所提出的基于非高斯态区分探测的往返式离散调制连续变量量子密钥分发方案的安全性,包括渐近情况与有限长效应情况.仿真结果表明所提出的方案相比于原始方案,即使在有信源噪声的情况下,其密钥率与最大传输距离仍然有明显的提升.这些结果表明本方案能够有效降低往返式离散调制连续变量量子密钥分发方案中非可信信源噪声对方案性能的负面影响,在保证系统实际安全性的同时,实现更高效、更远传输距离的量子密钥分发.

1 引言

量子密钥分发(quantum key distribution,QKD)[1-3]作为最成熟的量子密码技术之一,允许相隔两地的合法双方Alice 与Bob 在由攻击者Eve控制的不安全量子信道下生成安全密钥.基于量子力学的基本定律,理想化的QKD 方案已被证明是无条件安全的[4,5].目前采用的QKD 方案主要可分为两种: 离散变量(discrete variable,DV)QKD[6-8]与连续变量(continuous variable,CV)QKD[9-12].DV-QKD 主要依赖于造价高昂的单光子探测器技术,而CV-QKD 则是通过采用达到散粒噪声的相干探测器来提供安全性.与DV-QKD 相比,CVQKD 由于具有较高的探测效率以及易融于现有的光通信系统而备受关注.

在众多类型的CV-QKD 方案中,高斯调制相干态(Gaussian modulated coherent state,GMCS)方案的应用最为广泛[13].GMCS QKD 方案在实验室[14-17]以及现场试验[18]中均已被证明具有较好的可行性.在传统的GMCS QKD 实验方案中,为了获得用于信号探测的固定相位基准,发送方Alice将信号光与本振光安排在同一条量子信道中进行传输[13].然而,这种传输方式会导致系统出现安全漏洞.目前已报道的针对实际CV-QKD 系统的攻击策略包括本振光抖动攻击[19]、波长攻击[20]、校准攻击[21]以及饱和攻击[22],这些攻击策略均与CVQKD 系统中本振光的安全漏洞有关.此外,将光强度较高的本振光通过有损信道进行发送会大大降低QKD 的效率.

为了解决这些问题,2015 年,Qi 等[23]与Soh等[24]课题组各自独立提出单向本地本振(local local-oscillator,LLO)CV-QKD 方案,即在接收端用另外一台独立的激光器本地生成本振光.之后,LLO CV-QKD 方案得到进一步的拓展研究[25-28].在单向LLO CV-QKD 方案中无需将本振光与信号光一起进行传输,因此能够有效抵御针对本振光的攻击策略.然而,单向LLO CV-QKD 方案在实施过程中存在众多技术挑战,比如需要保证所使用的两台独立激光器能够生成同频率的信号光与本振光,对信号光进行相干探测时需要进行相位补偿等.此外,单向LLO CV-QKD 系统中存在的由环境扰动引起的偏振漂移,光纤长度波动以及两台独立激光器频率的不稳定性都会导致单向LLO CVQKD 方案性能及安全性降低.

为了解决单向LLO CV-QKD 方案中存在的不足,2016 年,Huang 等[29]提出本地本振往返式CV-QKD 方案.该方案无需采用两台独立的激光器来实现“本地本振”,因此具有较好的同频特性.不仅如此,往返式的光路结构可以对系统的偏振变化进行自适应补偿,从而更能够适应及满足实地应用的需求.

本地本振往返式CV-QKD 方案虽然能够很好地解决LLO CV-QKD 方案中所存在的不足,保证系统的实际安全性,但往返式GMCS CV-QKD 方案相比于单向点对点GMCS CV-QKD 方案,其系统中存在有更大的过噪声,并且在低信噪比远距离传输的情况下其协商效率非常低,严重限制了往返式GMCS CV-QKD 方案的最大传输距离.解决这个问题的方法是设计一种比LDPC 码更适用于低信噪比环境下的完美纠错码,然而设计并实施这样的一种纠错码复杂度高,并且所需的硬件成本也高.而另外一种解决的方法是采用离散调制.2002年,Silberhorn 等[30]最早将离散调制用于CV-QKD方案中.2009 年,Leverrier 和Grangier[31]对离散调制CV-QKD 的安全性进行证明并且发现离散调制(如四态调制)在低信噪比环境下可以获得更好的协商效率,从而实现更远距离的量子密钥分发.在离散调制CV-QKD 方案中,发送方准备一定数量的非正交相干态(如四态调制,非正交相干态的数量为4),并且利用所测量的每个相干态正则分量的符号来对密钥率比特进行编码.所测量的正则分量的符号为离散值,即使在低信噪比条件下,也能够很好地与高效纠错码配合使用.因此离散调制可以有效提高CV-QKD 方案的最大传输距离.

虽然高性能零差或外差探测器能够有效测量所接收到的量子信号,然而相干探测器中所固有的不确定性(电噪声)仍然会阻碍非正交相干态的精确分辨[32-34].即使所采用的探测器为理想探测器(量子效率为1),接收方仍然无法获得精确的测量结果.传统的理想探测器仅能达到标准量子极限(standard quantum limit,SQL),SQL 的定义是可以通过直接测量信号光的物理性质来区分非正交相干态所获得的最小误差.实际上,量子力学允许存在一个被称为Helstrom 界的误差下限,这个下限可以通过设计一种优秀的态区分策略来获得[35].2013 年,Becerra 等[32]提出了一种性能良好的态区分探测器用于无条件区分正交相移键控(quadrature phase-shift keying,QPSK)调制中的4 个非正交的相干态.该探测器通过利用光子计数及以快速反馈的形式进行的自适应测量的方式,从而接近或达到Helstrom 界.因此,采用性能良好的态区分探测器能够有效提升CV-QKD 方案的性能[36].

基于上述本地本振往返式光路结构、离散调制的使用优势,并且针对往返式光路结构中所存在的非可信信源噪声对方案性能的负面影响,本文提出基于非高斯态区分探测的往返式离散调制CVQKD 方案,即在探测端部署非高斯态区分探测器.所采用的态区分探测器可以满足在低于SQL 错误概率的情况下无条件区分出基于QPSK 调制的4种非正交相干态,即使往返式光路结构中存在信源噪声的情况下,相比于原始往返式离散调制CVQKD,本文所提出的方案仍能够有效提升密钥率与最大传输距离,从而能够获得更好的系统鲁棒性.本文第2 节详细描述了所提出的基于非高斯态区分探测的往返式离散调制CV-QKD 方案;第3 节对所提出的方案的安全性进行分析,包括渐近情况与有限长效应情况下方案的安全性;第4 节总结全文.

2 基于非高斯态区分探测的往返式离散调制CV-QKD 方案

首先介绍基于非高斯态区分探测的往返式离散调制CV-QKD 的制备-测量方案,之后介绍与之等价的基于非高斯态区分探测的往返式离散调制CV-QKD 的纠缠模型方案,最后介绍部署在探测端的非高斯态区分探测器原理.

2.1 基于非高斯态区分探测的往返式离散调制CV-QKD 制备-测量方案描述

在基于非高斯态区分探测的往返式离散调制CV-QKD 的制备-测量(prepare-and-measure,PM)方案中,Alice 将其中一束光强较高的经典光进行保留,用作本振光,而将另外一束光强较弱的经典光(同一个激光器生成)经过标准的光纤信道后发送给Bob,如图1 所示.Bob 在接收到由Alice发送的经典光后,对其进行离散调制.为了简化分析,此处主要分析离散调制中的四态方案[31].在四态调制方案中,Bob 从4 种类型的调制相干态中随机选取其中一种,然后借助于法拉第镜,经过透过率为T、过噪声为ξ的不可信信道反射回Alice 端.当经过非可信信道后,探测方Alice 利用分束器将发送过来的信号光一分为二,其中光强较高的信号光束(包含大多数光子)用于进行零差探测,而光强较低的信号光束(包含少数光子)则同步发送到态区分探测器中.则Alice 所接收到的混合量子态γ4=并对其进行零差探测,方案中Bob 端的离散调制方差VB=2α2,Alice 端实际零差探测器的量子效率为η,电噪声为υel,探测方Alice 的输入噪声为χhom.最后,经过经典后处理,Alice 和Bob 共享一串密钥.需要指出的是图1 中所示的信源由不可信第三方Fred 控制,并且为了更好地量化往返式离散调制CV-QKD 方案中的非可信信源过噪声,图1 中采用增益参数为g的相位非敏感放大器(phase-insensitive amplifier,PIA)来对方案中的非可信信源过噪声进行描述[29].需要指出的是,在实验环境中,往返式结构CV-QKD方案中的非可信信源噪声包含攻击者Eve 对信源进行窃听所引入的过噪声、Alice 进行脉冲调制所引入的噪声、Bob 端调制所引入的噪声以及激光器的相位噪声[29].在往返式结构CV-QKD 方案中,由于本振光并不随着信号光一起在信道中传输,而是可以直接在Alice 端本地生成,因此不会产生后向散射而引入系统过噪声.与单向CV-QKD 方案不同的是,在往返式结构的CV-QKD 方案中,Alice端为探测端,Bob 主要负责信号调制,即发送端.

图1 基于非高斯态区分探测的往返式离散调制CV-QKD 制备-测量方案图.DM 为离散调制,RNG 为随机数发生器,M 为调制器,QPSK 为正交相移键控,PIA 为相位非敏感放大器,FM 为法拉第镜,BS 为分束器,LO 为本振光,T 表示非可信信道的透过率,ξ 表示信道过噪声,g 表示相位非敏感放大器的增益参数Fig.1.Prepare-and-measure version of plug-and-play discrete modulation CV-QKD protocol based on non-Gaussian state-discrimination detection.DM,discrete modulation;RNG,random number generator;M,modulator;QPSK,quadrature phase shift keying;PIA,phase insensitive amplifier;FM,Faraday mirror;BS,beam splitter;LO,local oscillator;T,transmission efficiency;ξ,channel excess noise;g,gain parameters of phase insensitive amplifier.

2.2 基于非高斯态区分探测的往返式离散调制CV-QKD 纠缠模型方案

由于PM 方案不利于进行安全性分析,因此介绍与之等价的纠缠模型(entanglement-based,EB)方案,如图2 所示.Fred 制备纠缠态,其中模B发送给Bob,模A0则经过非可信信道发送给Alice.模A0与B的正则分量分别为以及〈 XB〉=〈PB〉=V,其中V=VB+1 并且非可信信源过噪声ξ0=(g-1)+(g-1)VI.此处VI表示真空态的噪声方差,g(g≥1) 表示PIA 的增益参数,用于衡量往返式离散调制CV-QKD 方案中的非可信信源过噪声ξ0的大小[29].Bob 利用外差探测器对模B进行测量,而模A0经过非可信信道后转换为模A1,Alice 对所接收到的模进行零差探测.值得一提的是,在图2 中,采用透过率为η的分束器以及方差为ν的辅助EPR 纠缠态来分别模拟Alice 端实际探测器的量子效率与电噪声.图2中M1和M2表示辅助EPR 纠缠态的一对纠缠模,并且M2与A2经分束器相互作用后得到模M3与A3.当经过非可信信道后,探测方Alice 利用分束器将发送过来的模A1一分为二,即模A2和模C.其中模A2(包含大多数光子)用于进行零差探测,而模C(包含少数光子)则同步发送到态区分探测器中用于提升系统性能.当Alice 和Bob 收集到足够多相关联的数据时,就可以利用经过认证的公共信道进行参数估计.最后,经过信息协商和保密增强,Alice 和Bob 就可以获得一串共享密钥.归结于信道输入端的总附加噪声χline=1/T -1+ξ,其中T表示信道透过率,ξ表示信道过噪声.

图2 基于非高斯态区分探测的往返式离散调制CV-QKD 纠缠模型原理图Fig.2.Schematic diagram of the entanglement-based (EB) model of plug-and-play discrete modulation CV-QKD protocol based on state-discrimination detection.

需要指出的是在往返式CV-QKD 方案中,Fred由攻击者Eve 控制,属于不可信的第三方.在EB方案中采用纠缠态来等价描述PM 方案中的带噪信源,纠缠态在往返式CV-QKD 方案中本质上是双模纠缠态,其计算方式与传统的双模压缩真空态的计算方式一样.而当Fred 是中立的第三方时,由于Fred 不受Eve 控制,即与Eve没有关联,在这样情况下可认为Fred 是与Alice及Bob 等价的合法通信方,则此时纠缠态就变成三模纠缠态[37-39].

其中I2表示 2×2 的单位矩阵,σ z=diag(1,-1),并且

值得一提的是,在纠缠模型中,Eve 能够对量子信道进行替换从而可以进行纠缠克隆攻击[40-42].在该攻击策略中,Eve 制备方差为R的辅助态|E〉来进行信息窃取,所替换的量子信道透过率为T,并且Eve 可以通过调整R的值来对应匹配真实信道的噪声χline=(1-T)/T+ξ.Eve 将辅助纠缠态|E〉其中一个模E2注入到分束器其中一个未使用端口,从而获得模E3,而对另一个模E1进行保留.当有脉冲经过信道时,Eve 都会重复上述过程,并将所收集到的辅助模E1和E3用量子存储器进行存储.最后,基于Alice 和Bob 所公布的经典通信信息,Eve 能够精确测量E1和E3的正交值.

图1 中制备-测量方案与图2 中纠缠模型方案两者等价处如下.

1)图1 制备-测量方案中,由于往返式结构CVQKD 信源是从Alice 发送给Bob,第三方Fred 可以对该经典信源进行控制.Bob 在接收到由Alice 发送的经典光后,对其进行离散调制,即从4 种类型的调制相干态k=0,1,2,3}中随机选取其中一种,然后借助于法拉第镜,经过透过率为T并且过噪声为ξ的不可信信道反射回Alice,这个过程等效为图2 中Fred 制备一个方差为V=VB+1 的纠缠态(记为|Φ〉),其中模B发送给Bob,模A0则经过非可信信道发送给Alice.Bob 对模B进行保留,并用外差探测进行投影测量|Φ〉〈Φ|,如果Bob 得到的测量结果为k,这就相当于制备了相干态,从而实现了往返式离散调制.此处V B=2α2即为图1中制备-测量模型的调制方差.

2)图1 中,在探测方Alice 处实际探测器的量子效率η等效为图2 中透率为η的分束器,图1 中实际探测器的电噪声υel则对应于图2 中方差为ν的辅助EPR 纠缠态其中一模式M2通过分束器后所引入的过噪声.对于图1 中制备-测量方案,探测方Alice 的输入噪声为χhom,则图2 中辅助EPR纠缠态方差ν的选择应满足探测器的总噪声在纠缠模型中同样为η χhom,因此在图2 纠缠模型中,

综上所述,图1 中的制备-测量方案等价于图2中纠缠模型方案.

2.3 部署在探测方Alice 处的非高斯态区分探测器原理

部署在探测方Alice 处的非高斯态区分探测器原理如图3 所示.该量子探测器可以满足在低于标准量子极限(standard quantum limit,SQL)错误概率的情况下无条件区分出基于四态离散调制的4 种非正交相干态.由图3 可知,本方案所采用的态区分探测器能够对相干态|α〉进行W次自适应测量.对于每次探测i(i ∈{0,1,···,W}),态区分探测器以当前经典寄存器中的数据为基准,制备一个具有最高概率的预测量子态之后利用位移算符D(δi) 对相干态|α〉进行位移变换,使得|α〉位移至随后采用一个光子数分辨探测器(photon number resolving detector,PNRD)对位移场的光子数量进行探测.假如探测得到表明预测态是正确的,Λ0发生响应,主要原因是输入场在位移置换的作用下被位移至真空,因此PNRD 无法探测到任何光子[32].需要指出的是,此处 Λ0响应意味着态区分策略对所输入的量子态进行正确的预测,预测成功则给定类别标记为h i=0,而预测失败类别标记则为h i=1 .经过i次自适应测量后,该策略根据当前标记集 ΞHist以及预测集采用贝叶斯推论,就能计算出所有可能态的后验概率.在下一轮中,指定具有最高概率的量子态作为反馈的输入态.需要指出的是,在本轮中δi已被加入到预测集同其他历史数据一起进行迭代以计算可能态的后验概率.因此,根据上述分析可知,所有可能态的概率在每一个反馈阶段都在进行动态更新,并且第i次反馈的后验概率则会转换为第i+1 次反馈的先验概率.贝叶斯推论的规则其表达式可写为

图3 非高斯态区分探测器原理图.PNRD 为光子数分辨探测器Fig.3.Schematic diagram of non-Gaussian state discrimination detector.PNRD,photon-number-resolving detector.

其中,Ppo({|α〉}|δi,hi) 表示后验概率,Ppr({|α〉})表示先验概率,Υ(hi|δi,{|α〉}) 表示对量子态|α〉进行位移操作后所观测到的结果hi的条件泊松概率,参数ϑ表示标准归一化因子.由于贝叶斯推论采用贝叶斯定理来对假设的概率进行更新,属于统计推论的一种方法,所给的信息越充分,推论也就越准确.因此,输入态|α〉在 经过W次自适应测量后,能够由第W+1 的预测态|δW+1〉 所决定[34].

从数学的角度考虑,标准量子极限区分采用QPSK 调制的非正交相干态,其失败概率的表达式可写为

表示QPSK 信号Gram 矩阵的特征值.由于在往返式方案中,Alice 为探测方,并且执行零差探测,因此在所提出的方案中将非高斯态区分探测器与零差探测器并行部署在探测方Alice 处.基于此,量子态的探测结果由零差探测器与非高斯态区分探测器共同决定.此处,为了更好地描述态区分探测器对往返式离散调制CV-QKD 方案性能的提升效果,可定义一个参数,即提升因子Ω,其表达式可写为[36]

3 方案安全性分析

本节在渐近情况[43]以及有限长效应情况[44]下对基于非高斯态区分探测器的往返式离散调制CV-QKD 方案进行安全性分析.

3.1 方案的渐近安全性

此处主要考虑反向协商下方案的渐近密钥率,并且为了简化分析,主要考虑探测端Alice 执行零差探测的情况.为了获得更加紧的安全界限,本方案假定第三方Fred 由攻击者Eve 控制,则所提出方案的渐近密钥率其表达式可写为

其中I o(A:B)=ΩoptI(A:B) 表示引入非高斯态区分探测器的往返式离散调制CV-QKD 方案中Alice 与Bob 的互信息量,I(A:B) 表示未引入非高斯态区分探测器的原始方案中Alice 与Bob 的互信息量,参数β表示方案的协商效率,Ωopt表示所采用的非高斯态区分探测器的最优提升因子,χ(A:E)表示Eve 从Alice 密钥中所窃取的信息量Holevo 界.此处将光纤的衰减系数设为ς,则光纤透过率的表达式T=10-ςL/10,其中L表示光纤长度.原始方案中Alice 与Bob 的互信息量I(A:B)的表达式可写为

接下来计算Alice 共扼零差探测器的加性噪声归结到信道输入端,其表达式可写为

其中,参数η和υel分别表示Alice 探测器的量子效率以及探测器电噪声方差.

由于信道加性噪声归结到输入端χline=1/T-1+ξ ξ,其中 表示非可信信道的过噪声[25].则归结到信道输入端的总噪声其表达式可写为

为了计算参数χ(A:E),此处假定Eve 无法对Alice 系统中的不完美器件进行攻击.该噪声评估模型已经被广泛应用于CV-QKD 实验中[15,19,28,29].基于此种噪声评估模型,Eve 和Alice 之间互信息量的Holevo 界χ(A:E) 的表达式可写为

接下来分析基于非高斯态区分探测的往返式离散调制CV-QKD 方案在渐近情况下的方案性能.涉及的仿真系统参数分别设定为V B=0.35,η=0.6,υel=0.05 .所提出方案的渐近密钥率与传输距离在不同增益参数g=1,1.003,1.005,1.01 下的关系如图4 所示,其中协商效率β=0.8 .此处g值的大小用于衡量非可信信源噪声的强弱,即g值越大,方案的非可信信源噪声强度越高.在图4 中也仿真出了Pirandola-Laurenza-Ottaviani-Banchi(PLOB)界,该界限表示点对点量子通信性能的最终极限[45].图4 中实线表示原始往返式离散调制CV-QKD 方案的性能曲线,而虚线则表示所提出的基于非高斯态区分探测的往返式离散调制CVQKD 方案的性能曲线.由图4 可以观察到,无论是在理想信源的情况(g=1,不存在信源噪声)还是在实际信源的情况(g ＞1,存在非可信信源噪声)下,所提出的方案性能始终优于原始方案的性能.即使在实际信源的情况下(g ＞1),所提出的方案其渐近密钥率与安全传输距离仍然显著优于原始方案的渐近密钥率与安全传输距离,并且所提出方案的性能更接近PLOB 界.比如当g=1.005 时,所提出方案的安全传输距离为90.8 km(绿色虚线),而原始方案的最大传输距离则不足50 km(绿色实线).这表明所提出的方案能够有效抵御往返式系统中非可信信源噪声对其性能产生的负面影响,相比于原始方案,受非可信信源噪声的影响更小.

图4 不同增益参数 g 下基于非高斯态区分探测的往返式离散调制CV-QKD 方案的渐近密钥率和传输距离的关系Fig.4.The relationship between the asymptotic secret key rate of plug-and-play discrete modulation CV-QKD protocol based on non-Gaussian state-discrimination detection and the transmission distance under different gain g .

图5 给出了所提出方案的渐近密钥率与协商效率β在实际信源 (g=1.005) 以及不同的传输距离L=40,50,60,70 km 下的关系.图中虚线表示所提出方案的性能曲线,实线表示原始方案的性能曲线.从图5 可以观察到,对于所提出的方案,协商效率β的可使用范围随着传输距离的增大而减小.相比于原始方案,本文所提出的方案在相同的传输距离以及协商效率下,其渐近密钥率始终高于原始方案的渐近密钥率.比如当传输距离L=40 km 以及协商效率β=0.8,所提出方案的渐近密钥率为0.004 bit/pulse,而原始方案的渐近密钥率仅为0.00066 bit/pulse.不仅如此,所提出方案其协商效率β的可使用范围显著大于原始方案中协商效率β的可使用范围.比如在L=40 km 的情况下,所提出方案的协商效率β的可使用范围为[0.65,1],而原始方案协商效率β的可使用范围仅为[0.775,1].

图5 在实际信源(g=1.005)与不同传输距离 L 下,基于非高斯态区分探测的往返式离散调制CV-QKD 方案的渐近密钥率与协商效率的关系Fig.5.The relationship between the asymptotic secret key rate of plug-and-play discrete modulation CV-QKD protocol based on non-Gaussian state-discrimination detection and the reconciliation efficiency under practical source(g=1.005) and different transmission distance L .

图6 给出了有无态区分探测器时,信噪比随不同信源条件(增益参数g的不同)的变化曲线.从图6 中可以发现在相同传输距离下,是否采用态区分探测,信噪比是存在差异的,即引入非高斯态区分探测器的方案(本文所提出的方案),其信噪比(实线)高于没有引入非高斯态区分探测器的方案(称为原始方案)的信噪比(虚线),并且随着增益参数g的增大,信噪比逐渐降低.而由图5 可知,所提出方案其协商效率的可使用范围显著大于原始方案中协商效率的可使用范围.主要原因在于所提出的方案的互信息量I o(A:B) 要大于原始方案的互信息量I(A:B),而根据(17)式可知,互信息量的增大使得本文所提出方案的信噪比 S NRo大于原始方案的信噪比 S NR,因此信噪比的变化使得所提出方案的协商效率与原始方案的协商效率适用范围不同.

图6 不同传输距离下L 下,基于非高斯态区分探测的往返式离散调制CV-QKD 方案的信噪比与增益参数g (不同的信源条件)的关系Fig.6.The relationship between the signal-to-noise ratio of plug-and-play discrete modulation CV-QKD protocol based on non-Gaussian state-discrimination detection and the gain g (different source conditions) under different transmission distance L.

3.2 有限长效应情况下方案的安全性

在上述渐近安全性分析中,对所提出的基于非高斯态区分探测的往返式离散调制CV-QKD 方案渐近密钥率计算的前提是假定Alice 和Bob 可以采用无限多的信号进行互换交流.然而这在实验中是无法实现的,主要原因是实际安全密钥的长度是有限的.因此有必要考虑有限长效应情况下所提出方案的安全性.则反向协商下所提出方案的有限长密钥率计算公式为[44]

其中I(A:B),β以及Ωopt的定义在上述分析中已给出.F表示所采集到的有效数据总长度,f表示Alice 和Bob 生成最终密钥所需的数据量长度,Q=F -f表示方案参数估计所需的数据量长度,εPE表示参数估计失败的概率,Δ(f) 则和保密增强相关联,其表达式可写为

其中HA表示与Alice 原始密钥相对应的Hilbert空间,表示平滑参数,εPB表示保密增强失败的概率.由于原始密钥是基于二进制比特来进行编码,因此 d imHA=2 .

由(32)式可计算(25)式中有限长效应影响下所提出方案的密钥率.

接下来分析所提出的基于非高斯态区分探测的往返式离散调制CV-QKD 在有限长效应情况下方案的性能.涉及全局的仿真系统参数与渐近情情况下所采用的仿真系统参数一致.图7 给出了在不同的有效数据总长度F=108,109,1010下所提出方案的有限长密钥率与传输距离的关系,并且也给出PLOB 界.图7(a)—(d)分别对应不同强度的非可信信源噪声,即g=1,1.003,1.005,1.01 .在图7(a)—(d)中也给出了渐近密钥率曲线以及PLOB界,用于参照对比.结合图7(a)—(d)可以发现,所提出方案的渐近密钥率(蓝色虚线)总是高于其有限长密钥率,然而随着F的增大,所提出方案的有限长密钥率曲线逐渐趋近于渐近密钥率曲线以及PLOB 界.此外,即使考虑有限长效应情况,所提出的方案其性能(虚线)无论是在理想信源的情况(g=1,图7(a))还是在实际信源的情况(g ＞1,图7(b)—(d))始终都要优于原始方案的性能(实线).这表明所提出的基于非高斯态区分探测往返式离散调制CV-QKD 能有效降低有限长效应,以及系统信源噪声对方案性能的负面影响.

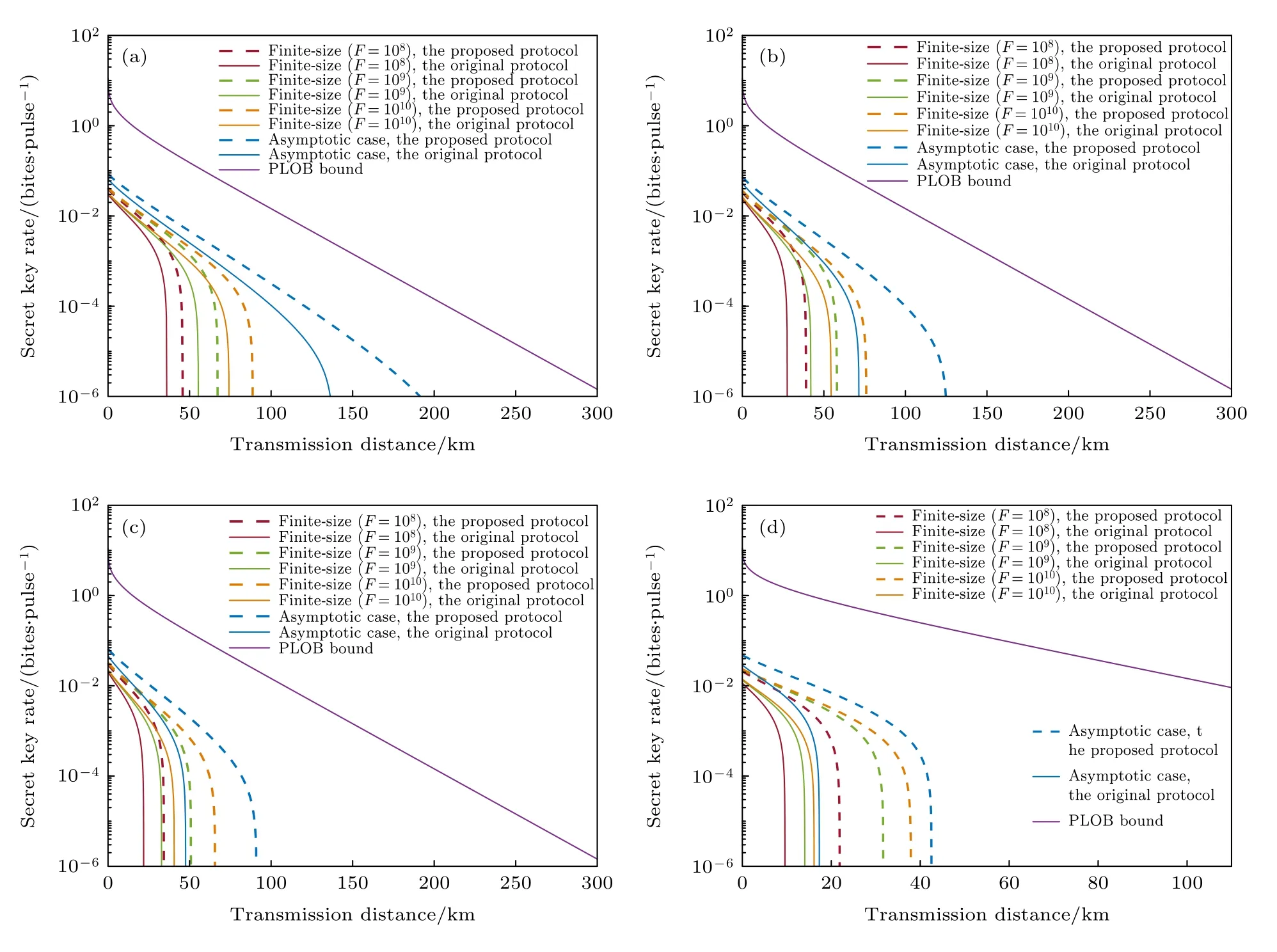
图7 在不同的有效数据总长度 F 下基于非高斯态区分探测的往返式离散调制CV-QKD 方案有限长密钥率与传输距离的关系 (a) g=1 ;(b) g=1.003 ;(c) g=1.005 ;(d) g=1.01Fig.7.The relationship between the finite-size secret key rate of plug-and-play discrete modulation CV-QKD protocol based on non-Gaussian state-discrimination detection and the transmission distance under different total exchanged signals F : (a) g=1 ;(b) g=1.003 ;(c) g=1.005 ;(d) g=1.01 .

4 结论

本文提出了一种基于非高斯态区分探测的往返式离散调制CV-QKD 方案,通过在探测方Alice 处部署非高斯态区分探测器,在满足低于标准量子极限错误概率的情况下无条件区分出基于四态离散调制的4 种非正交相干态,从而能够有效弥补往返式光路结构中非可信信源噪声对方案性能的负面影响.此外,对所提出的方案进行安全性分析,不仅考虑了其渐近安全性,同时也对有限长效应情况下方案的安全性进行分析,使得所获得的结果更符合实际情况.仿真结果表明本文所提出的基于非高斯态区分探测的往返式离散调制CVQKD 方案相比原始方案,无论是在理相信源情况(g=1)、实际信源情况(g ＞1)还是有限长效应情况,其性能都有明显的提升.不仅如此,本文所提出的方案其协商效率β的可使用范围显著大于原始方案中协商效率β的可使用范围.这表明所提出的基于非高斯态区分探测往返式离散调制CVQKD 方案能够有效降低有限长效应以及系统信源噪声对方案性能的负面影响.因此本文所提出的方案在保证系统实际安全性的同时能够实现更高效、更远传输距离的量子密钥分发.