压电陶瓷传感器监测混凝土内部缺陷的可行性研究
杨俊涛,左文建,张文龙,路国运,姜 珊
(1.太原理工大学土木工程学院,太原 030024;2.中铁三局集团投资有限公司,太原 030001)
0 引 言
混凝土结构因造价低、施工便利、抗压承载力好等优点,被广泛应用于建筑结构中[1]。然而,混凝土结构在服役过程中,由施工不当或材料本身原因等造成的内部初始缺陷会不断扩展,使其承载力降低,影响建筑结构的安全性和耐久性[2]。为减少和避免混凝土内部缺陷发展造成的经济损失,及时对其进行健康监测十分必要。
混凝土结构内部缺陷监测在文献中得到了广泛关注。目前混凝土内部缺陷的监测方法主要有超声波法[3]、声发射法[4]、图像处理法[5]、雷达法[6-8]、红外成像法[9-11]等。然而,上述方法大多需要专业监测设备及技术人员的参与,成本较高,费时费力,难以实时获取结构缺陷信息、预测结构健康状况,且结构复杂的建筑还存在难以检测到的位置[12]。而基于压电传感器(piezoceramics transducer,PZT)的声发射法具有响应快、灵敏度高、具备传感和驱动双重功能等优点可逐步应用于结构健康监测领域[13-15]。

为此,本文采用PZT,结合主动监测技术对4组共7个带内部缺陷的混凝土试件进行试验研究,探索一种混凝土缺陷监测和缺陷位置识别的方法。试验中,将不同尺寸的塑料空心球埋置在混凝土试件的不同位置,模拟混凝土内部缺陷,将压电传感器粘贴在养护好的混凝土表面,用于监测混凝土内部缺陷情况。不同大小的缺陷使传感器接收的信号幅值产生不同程度的衰减,基于时域信号构造能量指数及损伤参数,并建立其与缺陷大小的函数关系,定量分析混凝土内部缺陷程度。对比不同区域的能量指数与损伤参数,判定混凝土内存在缺陷的区域,以期探索PZT监测混凝土内部缺陷位置及缺陷程度的可行性。
1 压电陶瓷传感器的主动监测方法
基于PZT的主动监测方法是指在待测结构上安装两枚PZT,一枚作为驱动器,另一枚作为传感器。基于PZT的正逆压电效应,通电激励驱动器产生应力波,在混凝土内部传播,同时另一枚传感器接收通过待检测区域的应力波并将其转化为电信号,其监测原理如图1所示[25]。

图1 混凝土内部缺陷监测原理图Fig.1 Schematic diagram of internal defect monitoring of concrete
监测过程中,由于内部缺陷的存在,应力波在缺陷附近传播时发生反射和绕射等现象,使PZT接收的电信号幅值降低,信号能量衰减。基于此原理,可建立基于信号幅值、能量的相关参数:能量指数和损伤参数。并建立参数与混凝土缺陷程度的函数关系,定量描述混凝土内部缺陷程度。
2 混凝土结构内部缺陷监测方法
2.1 损伤评定参数
针对扫频模式及五峰值模式,有学者[24]证明基于信号能量及幅值建立的参数能较好反映混凝土裂缝损伤程度。因此可以定义基于扫频接收信号的能量指数EIK,基于五峰值脉冲信号的损伤参数RA来反映结构缺陷程度。信号能量EK的表达式为
(1)
式中:xn为信号的离散点;n为采样点数。计算能量指数EIK,并以此表征待检测结构不同区域的缺陷程度,EIK定义为
(2)
式中:能量指数EIK表示在PZT监测范围内,每个PZT接收到的信号能量值与监测区域内所有PZT接收到的信号能量平均值的对比。若某一监测区域的EIK小于1,即响应信号的能量值小于监测区域内所有响应信号的能量平均值,则该区域存在缺陷的概率最大,且能量值相差越大,内部缺陷程度越大。
在五峰值脉冲模式下接收的响应信号,定义损伤参数RA为
(3)
式中:x0(t)为健康区域接收的时域信号;xj(t)为损伤区域接收的时域信号。(t2-t1)对应接收信号的一个周期。若某一区域无损伤时,RA值为0,当缺陷程度越大时,RA值越小并趋近于1。
2.2 结构损伤的定位方法
采用PZT定位混凝土内部缺陷时,将PZT按照一定规律布置在结构上。此时,混凝土结构被分割成多个区域,采用一对PZT监测每个区域,当某一子区域产生缺陷损伤时,可根据PZT接收的信号变化及变化程度确定缺陷位置和缺陷程度。分割子区域类似于有限元中划分网格,网格划分越密集,计算结果越精确,但是对计算平台要求越高,计算时间越长,而稀疏的网格又会降低其计算精度。同理,结构中布置的PZT数量越多,子区域的范围越小,缺陷定位越精确,相反结构中布置的PZT数量越少,子区域的范围越大,缺陷定位精度降低。因此,PZT的数量需根据结构尺寸、形状及实际需求综合考虑。
根据待检测结构形状的不同,将PZT以一维、二维和三维的形式布置在结构中,如图2所示。
图2 PZT在不同结构中的布置形式Fig.2 Layout form of PZT in different structures
由图2可以看出每一个PZT在混凝土试件中的位置是固定不变的,可以依据PZT的相对位置和监测结果对缺陷的位置进行定位,可通过EIK值和RA值的变化判断缺陷位置和缺陷程度。文中混凝土试件已养护完成,将压电传感器粘贴在试件表面,当其中某些压电传感器出现异常时,便于及时更换,保证监测过程实时进行。
3 混凝土结构内部缺陷监测试验
3.1 混凝土试件及试验装置
试验中混凝土试件尺寸为320 mm×100 mm×100 mm。在浇筑混凝土前,在模具内的标定位置绑扎塑料空心球,使混凝土内部出现介质不均匀的区域,以此模拟混凝土内部缺陷。将搅拌好的混凝土浇筑在设计好的模具中,在标养条件下养护28 d,混凝土配合比见表1。在混凝土试件表面粘贴4枚PZT,压电陶瓷的型号为PZT-5H,选用的粘合剂为上海康达公司的双组分环氧树脂,在粘贴时用手指轻轻按压PZT,挤出多余的胶水,防止粘结层过厚降低PZT与试件间剪力传递效率,PZT在混凝土试件中的布置图如图3所示。

表1 混凝土配合比Table 1 Concrete mix ratio

图3 PZT在混凝土试件中的布置图Fig.3 PZT layout diagram in concrete specimen
混凝土试件内部缺陷监测系统包括AFG 1022任意函数/波形发生器、功率放大器、混凝土试件、NI USB-6366数据采集卡、PZT、安装LabVIEW软件的笔记本电脑,如图4所示。试验中波形发生器产生电信号,电信号经过功率放大器后激励驱动器产生应力波在混凝土中传播,数据采集系统接收传感器的响应信号。在监测过程中,信号类型有正弦线性扫频和五峰值脉冲,数据采样频率为100 kHz。扫频波参数:起始频率f0为100 Hz,截止频率f1为100 kHz,总时长T为1 s,幅值A为5 V。五波峰信号通过软件Arb Express调试,由信号发生器产生,其中心频率为10 kHz,幅值为5 V。

图4 试验监测系统Fig.4 Test monitoring devices
3.2 试验设计
试验中,浇筑四组共7个混凝土试件,试件内部缺陷设置情况如表2所示。其中C0作为对比试件,不埋入空心塑料球。为防止混凝土振捣过程中塑料空心球上浮,通过细铁丝将空心球固定在混凝土模具中,具体埋置情况见图5。

表2 混凝土试件内部缺陷情况Table 2 Internal defects of concrete specimens

图5 以塑料空心球为内部缺陷的混凝土试样示意图Fig.5 Schematic diagrams of concrete specimens with plastic hollow ball as internal defect
在第1组试验中,以PZT2作为驱动器发射信号,以PZT3作为传感器接收信号,对所有试件进行监测,两枚传感器的间距为270 mm,具体工况见表3。第1组试验目的是研究压电传感器位置固定的情况下,监测信号随试件内缺陷的位置、大小变化的规律。

表3 第1组试验工况Table 3 Test conditions of first group
在第2组试验中,通过4枚压电传感器将B、C组的混凝土试件划分为Ⅰ、Ⅱ、Ⅲ三个监测区域,并对混凝土试件的不同区域进行监测,具体工况见表4。监测区域Ⅰ中PZT1发射信号,PZT2接收信号,设为工况3;监测区域Ⅱ中PZT2发射信号,PZT3接收信号,设为工况4;监测区域Ⅲ中PZT3发射信号,PZT4接收信号,设为工况5,各PZT对的间距为90 mm。对比不同工况监测结果,确定缺陷存在区域。

表4 第2组试验工况Table 4 Test conditions of second group
4 结果与讨论
4.1 第1组试验结果分析
采用扫频模式对混凝土试件进行监测,第1组试验接收到的信号时域如图6所示。可以看出随着试件内的缺陷程度增大,信号幅值不断减小。工况1、2下,传感器从试件C0获取的时域信号幅值最大,其峰值为0.014 V;传感器从试件C1-50、C2-50获取的时域信号幅值最小,其最大值均在0.006 V左右。原因在于随着混凝土内部缺陷程度增大,缺陷对应力波的反射效果越明显,传感器接收到的信号幅值不断减小。

图6 第1组试验扫频模式下信号时域图Fig.6 Time domain diagram of signal in frequency sweep mode of first group test
为了定量分析接收到的信号强弱程度,计算同一工况下传感器接收的信号能量值,并将其平均值作为基准值,通过式(2)计算信号的能量指数EIK,结果如图7所示:在两种工况下,当混凝土试件无缺陷时,EIK最大,分别为167.8%和172.1%;随着内部缺陷程度的增大,EIK不断减小,最大减小幅值分别为52.0%、53.3%,对应缺陷直径由30 mm变为50 mm,即缺陷体积变化最大的情况,符合实际情况。当缺陷位置发生改变而传感器位置和缺陷程度不变时,其EIK相近,各组两个试件的差值在2.5%以内。这说明当PZT的位置固定时,其接收的信号能量只与缺陷大小有关。

图7 第1组试验扫频模式下能量指数EIK值变化图Fig.7 Change diagram of energy index EIK value in frequency sweep mode of first group test
以两种工况下缺陷程度相同时测得的信号能量指数EIK的均值作为因变量,缺陷直径D作为自变量,建立两者间的函数关系。
EIK=189.04e-0.031×D(0≤D<100)
(4)
式中:EIK单位为%。式(4)对D求导后结果为

(5)
可以看出,能量指数与混凝土梁构件内部缺陷的直径呈负相关。在无损伤情况下,能量指数EIK值最大,随着缺陷程度增大,EIK值逐渐趋近于0。因此采用能量指数能较好地反映混凝土内部缺陷程度。
五峰值脉冲信号的监测结果如图8和图9所示,图8表示采用五峰值脉冲信号对C0进行监测的结果。由图8可见响应信号的周期为1 ms,因此对五峰值脉冲模式下的响应信号截取1 ms进行分析。图9中(a)、(b)分别表示工况1、2下的信号时域图。从图中可以看出,在五峰值模式下,传感器测得的信号幅值也可以反映混凝土缺陷程度变化。当试件内无缺陷时,其幅值最大为0.69 V,随着缺陷程度增大,信号幅值减小。为了定量描述混凝土缺陷程度与信号幅值的大小,采用式(3)计算不同缺陷程度下的损伤指数RA,如图10所示。可知缺陷直径不变时,缺陷位置的改变不会影响损伤指数RA,此结果与扫频信号的监测结果一致。
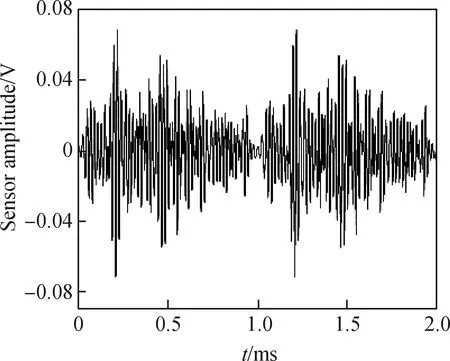
图8 五峰值脉冲模式下无缺陷状态的信号时域图Fig.8 Time domain diagram of signal in detection-free state in five-peak pulse mode

图9 第1组试验五峰值脉冲模式下信号时域图Fig.9 Time domain diagram of signal in five-peak pulse mode of first group test

图10 第1组试验五峰值脉冲模式下损伤指数RA变化图Fig.10 Change diagram of damage index RA in five-peak pulse mode of first group test
以两种工况,同一缺陷程度下的损伤指数RA为因变量,以缺陷直径D为自变量,建立RA与D间的函数关系,如式(6)所示。
RA=1-0.710.164+0.143×D(0≤D<100)
(6)
第1组试验五峰值脉冲模式下损伤指数RA变化如图10所示,可以看出,缺陷直径与损伤指数RA近似呈指数关系,随着混凝土缺陷直径的增大,损伤指数逐渐增大并趋近于1,且其拟合度为0.98,因此可根据定义的损伤指数确定混凝土内部缺陷程度。
通过上述两种模式对混凝土内部缺陷监测试验的结果表明:本文所采用的两种信号波形及对应的两种参数均能较好反映混凝土内部缺陷大小。在某一监测区域内,压电传感器布置的位置固定,混凝土缺陷程度不变时,缺陷位置变化对EIK和RA的影响很小。
4.2 混凝土内部缺陷位置探测试验
图11给出了第二组试验在工况3、4、5下,扫频模式的响应信号。由图可见,同一试件,传感器在健康区域接收的时域信号幅值明显大于缺陷区域。且随着缺陷增大,健康区域和缺陷区域的信号幅值相差越大。此外,不同试件的健康区域时域信号峰值接近,但波形存在差异,而同一试件无缺陷的两个监测单元时域信号波形相似,原因在于混凝土为非均质材料,不同试块的粗骨料数量和排布方式、振捣密实程度均有差别,但同一试块,混凝土内部情况接近,因此接收的时域信号波形相似。

图11 第2组试验在扫频模式下信号时域图Fig.11 Time domain diagram of signal in sweep mode of second group test
图12给出了试件在不同工况下的能量指数EIK值变化图。由图12(a)可以看出,各试件在工况3下的EIK值明显小于其余两种工况,而工况4、5下的EIK值接近,由此可以判断缺陷只发生在区域Ⅱ,监测区域Ⅱ和Ⅲ未发生缺陷。由图12(b)可以看出,与监测区域Ⅰ和Ⅲ相比,内部存在缺陷,这与实际缺陷情况吻合。对比不同试块在健康区域的EIK值后发现其离散型较大,为了减小不同试块测得数据的离散型,说明不同缺陷程度对测试结果的影响,对试块三个区域求得的EIK值进行归一化处理:以三个区域EIK值的和为基数,求解缺陷区域EIK值所占比例,其结果如图13所示。可以看出,随着缺陷直径的增加,缺陷区域的归一化指数减少,且混凝土缺陷程度相同时,得到的归一化指数接近,证明能量指数可以较好地反映混凝土缺陷程度变化。

图12 第2组试验不同工况下的能量指数EIK值变化图Fig.12 Change diagram of energy index EIK value under different working conditions of second group test

图13 混凝土试件缺陷区域归一化指数变化图Fig.13 Change diagram of normalized index of defect area of concrete specimens
图14给出了第2组试验在五峰值脉冲下传感器的响应信号。由图可知各试件在健康区域接收的信号最大幅值在0.1 V左右,随着缺陷直径增大,信号时域幅值减小。还可以看出试件C1-20、C1-30、C1-50在工况3下信号幅值明显低于工况4、5下的信号幅值,试件C2-20、C2-30、C2-50在工况4下的信号幅值明显低于工况3、5下的信号幅值。

图14 第2组试验在五峰值脉冲模式下信号时域图Fig.14 Time domain diagram of signal in five-peak pulse mode of second group test
提取信号幅值较大的两个工况下的时域信号,并将健康区域的两组信号的平均值作为基准值,求得各试件在不同工况下的RA值并绘制变化曲线,如图15所示。试件C1-20、C1-30、C1-50在工况4、5下的损伤指数相近且小于工况3,试件C2-20、C2-30、C2-50在工况3、5下的损伤指数相近且小于工况4,由此可确定试件C1-20、C1-30、C1-50的缺陷存在于监测区域Ⅰ,试件C2-20、C2-30、C2-50的缺陷存在于监测区域Ⅱ。试验证明,可通过五峰值波定位混凝土试件中存在缺陷的损伤区域。

图15 第2组试验不同工况下RA值Fig.15 RA values under different working conditions of second group test
通过扫频波和五峰值波对混凝土梁中缺陷位置探测的试验表明,本文采用的波形以及提出的参数能够较好确定混凝土内存在缺陷的区域。需注意,这种缺陷定位方式只是一种近似方法,缺陷位置的准确度与压电传感器在结构中布置的数量有关。
5 结 论
针对以往方法对混凝土结构缺陷监测的不足,本文探索一种基于应力波理论的压电传感器主动监测技术,对混凝土内部缺陷程度进行判定和损伤区域确定的方法。主要的结论如下:
(1)混凝土内部缺陷监测试验结果表明,基于扫频信号和五峰值脉冲信号建立的能量指数EIK与损伤指数RA对混凝土内部缺陷程度变化敏感。当缺陷程度增加时,EIK值较小并趋近于0,RA值越大并趋近于1。因此,可通过EIK、RA判定内部缺陷程度。且当传感器位置固定、缺陷程度相同时,缺陷位置的变化不会影响EIK和RA值。
(2)采用压电传感器阵列的方式对混凝土结构不同区域进行监测,由于内部缺陷的存在,应力波在该区域传播过程中幅值衰减,能量降低,通过EIK值和RA值的变化定位其缺陷区域。

