基于暂态能量比的交流输电线路故障选相方法

黄明伟，王力，周仕豪，曾祥君

（1.长沙理工大学电气与信息工程学院，湖南长沙 410114；2.江西省电力有限公司电力科学研究院，江西南昌 330096）

0 引言

在电力系统中，高压输电线路承担着传输大容量电能的重要任务。为确保系统的稳定运行，需要及时切除线路发生的故障[1]。因此，必须对线路应用继电保护和自动重合闸等技术[2]，而在自动重合闸在动作之前必须先完成快速、准确地故障选相[3-5]。传统的输电线路故障选相方法，主要包括稳态量法、故障分量法以及二者结合的方法。基于稳态量的选相方法，包括电流选相、电压选相、阻抗选相及序分量选相，易受系统运行方式、过渡电阻及强弱电源等因素影响，一般需配合其他选相方法；基于故障分量的选相方法包括相电流差法、相电压差法及复合电压电流法。相电流差法存在弱电源侧灵敏度不足的问题[6-8]，相电压差法则存在强电源侧灵敏度不足[9]，复合电压电流法在三相故障选相方面存在问题[10]；而基于二者结合的方法，实际应用中误选相事故也时有发生[11]。

随着新兴数字信号技术的发展，对故障信息的处理能力大为提升，出现了许多新的故障选相方法，较为典型的是利用小波变换提取故障后的暂态特征实现选相[12-14]。如对暂态电流行波进行小波分解获取暂态信号的时频特征，并通过时频相关系数和时频特征向量实现故障选相[12]。利用小波分解获取暂态分量中的衰减直流分量在不同故障情况下的特征实现选相[13]。通过对故障后的暂态分量进行相模分解和S 变换构建选相方案，但仍需结合相电流积分量区分两相短路接地[14]。除了获取暂态信息外，利用小波方法构造暂态能量亦能实现故障选相。如通过比较三相能量的相对大小来识别故障类型和故障相别[15]。文献[16]对电压暂态信号进行小波变换后构建出一种无须两端信号同步的高压输电线路选相方法。文献[17]利用小波变换获取电流行波模分量的能量进行故障选相。这些基于小波的选相方法，存在母小波选取原则不清、初始行波波头易受过渡电阻、故障初相角等外部因素影响，不利于实际应用。

鉴于小波方法存在的问题，有学者利用其他方法构建暂态能量实现故障选相与定位。文献[18]提出一种基于零序电流首容性分量能量的小电流接地故障的区段定位方法。文献[19]利用电压和电流的故障分量计算暂态能量，并根据阻性暂态能量的正负实现谐振接地系统中故障选线，但其未能进一步实现故障选相。文献[20]通过采样电压、电流信号构建虚拟瞬时能量比实现故障选相，但其面临选相阈值设定复杂的问题。

鉴于目前各种基于暂态能量选相方法存在算法和判据复杂、难以适应多种故障场景的问题，本文基于能量的物理含义，利用电压和电流故障分量计算三相暂态能量比和零序暂态能量，并构造选相判据实现准确地故障选相。结合动模试验与PSCAD/EMTDC 仿真数据验证了本文选相方法的可靠性。

1 暂态能量比的构建

双端电源系统结构如图1 所示。图1 中，EP，EQ为系统两端等效电源；LP，RP为P侧系统等效电阻和电感；LQ，RQ为Q侧系统等效电阻和电感；LBP，LBQ为输电线路P，Q两侧的并联电抗器；K1，K2，K3 为设置的不同故障点。

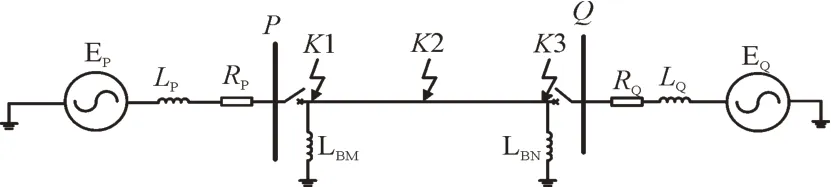
图1 双端电源系统Fig.1 Double-ended power supply system

基于图1 系统中K3 点A 相金属接地（AG）动模试验，其故障前后1 周波的数据如图2 所示，其中横坐标N为采样点数。采样频率为10 kHz。由图2 波形可知，当输电线路发生故障后，故障相电流较故障发生前增大、故障相电压有所降低且由于三相之间耦合影响，非故障相电流和电压也发生变化，但要明显小于故障相。对于各种故障下电气量变化的理论分析已有大量研究，本文不再赘述[8，10]。

图2 故障前后一周波电压、电流波形Fig.2 One-cycle voltage and current waveforms before and after fault

本文从故障分量的角度，利用各相故障分量的差异构建暂态能量。故障分量的精确获取是一个较为复杂的问题。当线路发生故障后，发电机励磁调节器作用、负荷变化等因素，均会对计算结果产生影响。在工程实际中，一般基于全周相减法[7]获得故障分量，其运算式为：

式中：X为电压或电流；ΔX(t)为故障分量；X(t)，X(t-T)分别为故障后和故障前采样电气量；t为采样时刻；T为工频周期。

本文利用故障前后各1/4 周波数据计算，后文图将利用图2 故障前后各1/4 周波数据计算，对应采样点从150 至250。对图2 的动模试验故障录波数据，通过式（1）获取各相电流和电压故障分量绝对值|Δik（t）|，|Δuk（t）|，k=a，b，c；计算得到的故障分量绝对值波形如图3 所示。由图3 波形可知，故障相的故障分量最大，非故障相故障分量小于故障相且近似相等。

图3 电流、电压故障分量波形Fig.3 Current and voltage fault component waveforms

为进一步判别接地故障，定义零序故障分量ΔX0：

式中：X0（t）为故障后t时刻零序电压或电流值；X0（t-T）为故障前一周期t时刻的零序电压或电流值；Xk（t）为故障后一周波t时刻各相电压或电流采样值；Xk（t-T）为故障前一周波t时刻各相的电压或电流采样值。

通过式（2）计算零序电流和电压故障分量绝对值，其波形如图4 所示。由图4 波形可知，当发生接地故障后，零序电流和零序电压存在明显突变。

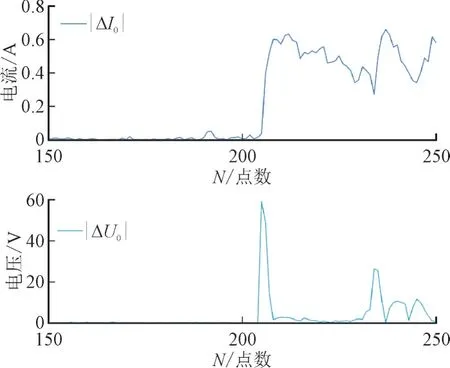
图4 零序电流、零序电压故障分量波形Fig.4 Zero-sequence current and voltage fault component waveforms

类比单相瞬时有功功率[21]，定义暂态功率突变值为：

式中：Δpj(t)为三相或零序暂态功率突变值；|Δuj(t)|为电压故障分量绝对值；|Δij(t)|为电流故障分量绝对值，j=a，b，c，0。

进一步对暂态功率突变值积分得到暂态能量：

式中：Wj为三相暂态能量Wa，Wb，Wc或零序暂态能量W0；t0为故障初始时刻；Δt为数据窗长。

为便于离散采样数据计算，将式（4）离散化：

式（5）中N对应故障前后各1/4 周波，N=100。

根据式（3）和式（5）计算暂态功率和暂态能量，其波形如图5 所示。由图5 可知，AG 金属性故障时，A 相暂态能量远远大于非故障相，且零序暂态能量大于0。

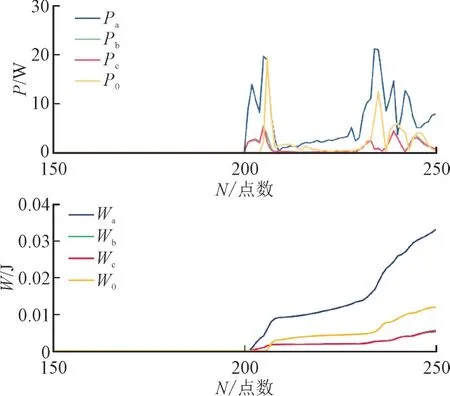
图5 暂态功率、暂态能量突变值波形Fig.5 Waveforms of sudden change in transient power and transient energy

基于式（5）计算各种类型故障的暂态能量，其中ABG，AB，ABC 故障时的计算结果如图6 所示。由图6 波形可知，相间故障时，两故障相的暂态能量远大于健全相且零序暂态能量接近于0；相间接地短路时，零序暂态能量非零，故障相暂态能量同样远大于非故障相；三相短路时，三相的暂态能量接近相等，零序暂态能量同样接近于0。

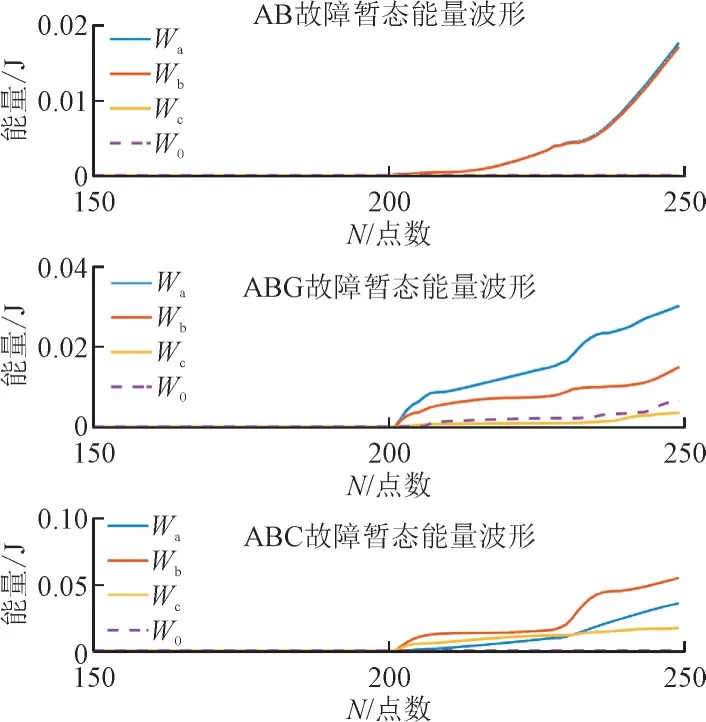
图6 AB，ABG，ABC故障暂态能量波形Fig.6 Waveforms of transient energy during fault of AB，ABG，ABC

为定量反映三相暂态能量之间的关系，考虑通过利用故障前后各1/4 周波数据积分所得三相暂态能量同除以其中的最小值，得到三相暂态能量比为：

式中：Wk为三相暂态能量；min(Wk)为三相暂态能量最小值；WRk为三相暂态能量比值。

2 选相方法

结合动模试验获取的故障录波数据及大量仿真数据计算的特征量，将基于暂态能量比的线路故障选相方法表述如下：

1）在识别故障后，取故障前1周波中前后各1/4周波数据，通过式(5)计算得出Wa，Wb，Wc和W0。

2）根据式(6)计算三相暂态能量比值并按数值大小依次记为：WRmax，WRmid，WRmin。

3）若W0＞ε0，则判定为接地型故障，ε0为判别接地故障的阈值；当暂态能量3 个比值中有2 个接近于1，即WRmid/WRmin＜ε1，则判定为单相接地故障，WRmax对应的相别为故障相；反之，则为相间接地故障，WRmax，WRmid对应的相别为故障相；ε1为判别单相接地故障的阈值。

4）若W0＜ε0，则判定为不接地故障；当3 个比值中最大值与最小值差别不大，即WRmax/WRmin＜ε2，则判定为三相故障；反之则为相间故障，WRmax，WRmid对应的相别为故障相；ε2为判别三相故障的阈值。

根据1）-4）的计算步骤，构建基于暂态能量比的故障选相方法，其选相流程如图7 所示。

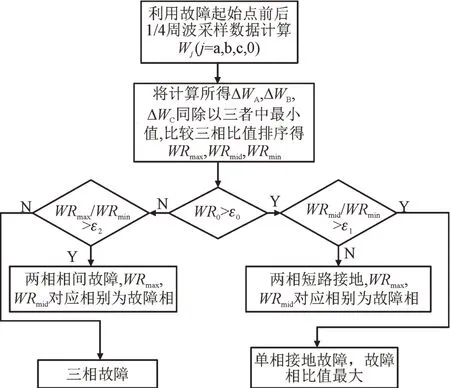
图7 基于暂态能量比的选相流程图Fig.7 Flowchart of phase selection based on transient energy ratio

3 仿真验证与分析

3.1 不同故障类型选相结果

根据某实际线路（如图1 所示）动模试验所获取的10 种类型故障的录波数据，按照本文所提方法对其进行故障选相，根据式（5）、式（6）计算的三相暂态能量比和零序暂态能量如表1 所示。大量的仿真分析表明，图8中ε0取0.01 可分辨出接地故障；ε1取1.1 可辨别出单相接地和相间接地故障；ε2的取值裕度非常大，取为10～1 000 均可区分三相短路和两相短路故障。

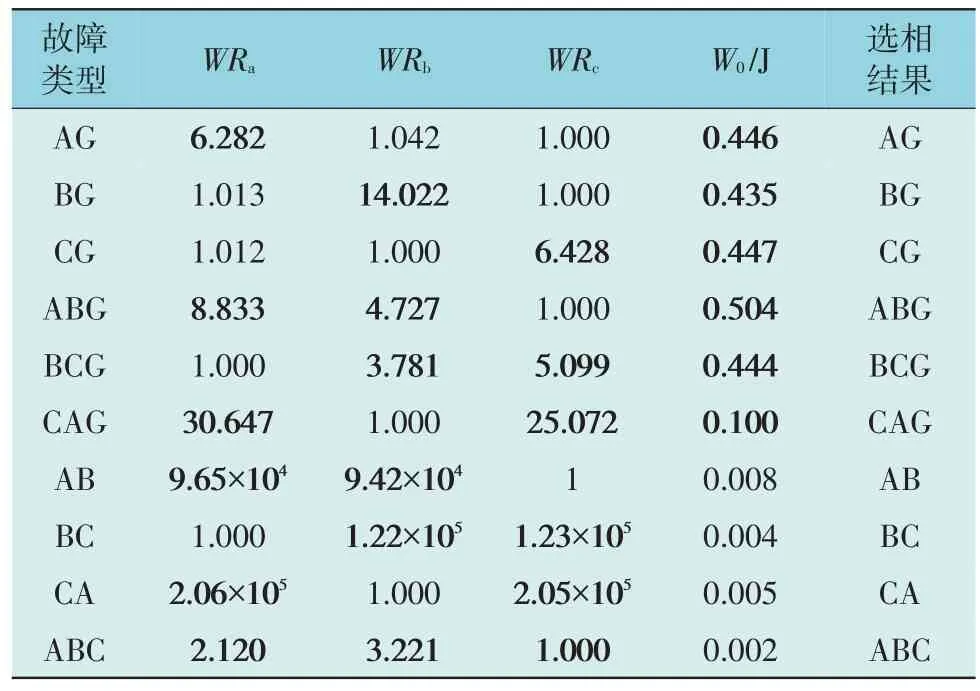
表1 不同故障类型选相结果Table 1 Phase selection results of different fault types

表1 中，AG，ABG，AB，ABC 依次为A 相接地故障，AB 相间接地故障，AB 相间短路故障，ABC 三相短路故障，其余不同相别的故障可类似推之。由表1 可知，根据三相暂态能量比和零序暂态能量可以准确地实现故障选相。

为进一步验证本文方法在线路不同位置故障、经过渡电阻故障、不同故障初相角以及在弱电源侧发生故障的选相性能，通过搭建仿真模型，对各种工况下的故障选相结果进行验证。

3.2 仿真模型构建

结合京津唐500 kV 高压输电线路参数[8]，在PSCAD/EMTDC 中搭建如图1 所示的分布参数输电线路模型，长度为300 km，仿真系统参数如下。

电源参数：P侧电源零序电抗LP0=0.092 6H，零序电阻RP0=0.6 Ω，正序电抗LP1=0.137 43H，正序电阻RP1=1.051 5 Ω；Q侧电源零序电抗LQ0=0.119 27H，零序电阻RQ0=20Ω，正序电抗LQ1=0.14298H，正序电阻RQ1=26 Ω。

线路参数：单位正序电阻r1=0.020 83 Ω/km，单位正序电感l1=0.894 8 H/km，单位正序电容C1=0.012 9 μF/km；单位零序电阻r0=0.114 8 Ω/km，单位零序电感l0=2.2886H/km，单位零序电容C0=0.00523μF/km。

并联电抗器补偿度为70%，线路两侧分别整定为：LBP=7.480 3 H，LBQ=2.493 4 H。

为验证仿真系统的合理性，限于篇幅，以AG故障时的波形为例进行阐述，将K3 点AG 故障时三相和零序电压、电流故障分量的波形绘制于图8 中。对比图3、图4 和图8 中对应的三相和零序故障分量的波形，可见在AG 故障时仿真系统与动模试验的结果具有同样的特征，说明本文方法同样适用于分析PSCAD 中搭建的京津唐500 kV 线路仿真系统。

图8 AG故障时各故障分量波形Fig.8 Waveforms of each fault component during AG fault

进一步分析表1 中10 种故障类型下不同故障位置、过渡电阻、故障初相角以及弱电源侧故障等情况的选相方法适用性。

3.3 不同过渡电阻的仿真

在已有的文献研究中，过渡电阻一般取值都不超过300 Ω[8]。为了验证本文所提选相方法耐受过渡电阻的能力，在图1 所示线路中K1、K2、K3 点，将过渡电阻从0 Ω开始，以100 Ω为步长增加至1 000 Ω，对不同过渡电阻下的各种类型故障进行仿真，故障时间设置为1 s。K3 点经不同过渡电阻故障情况下的选相结果如表2 所示。

由表2 可知，当过渡电阻达到900 Ω后，出现AG 选相失败的问题。说明采用暂态能量比的选相方案较传统突变量方法可耐受更大的过渡电阻，至少可以实现800 Ω以下过渡电阻的正确选相。

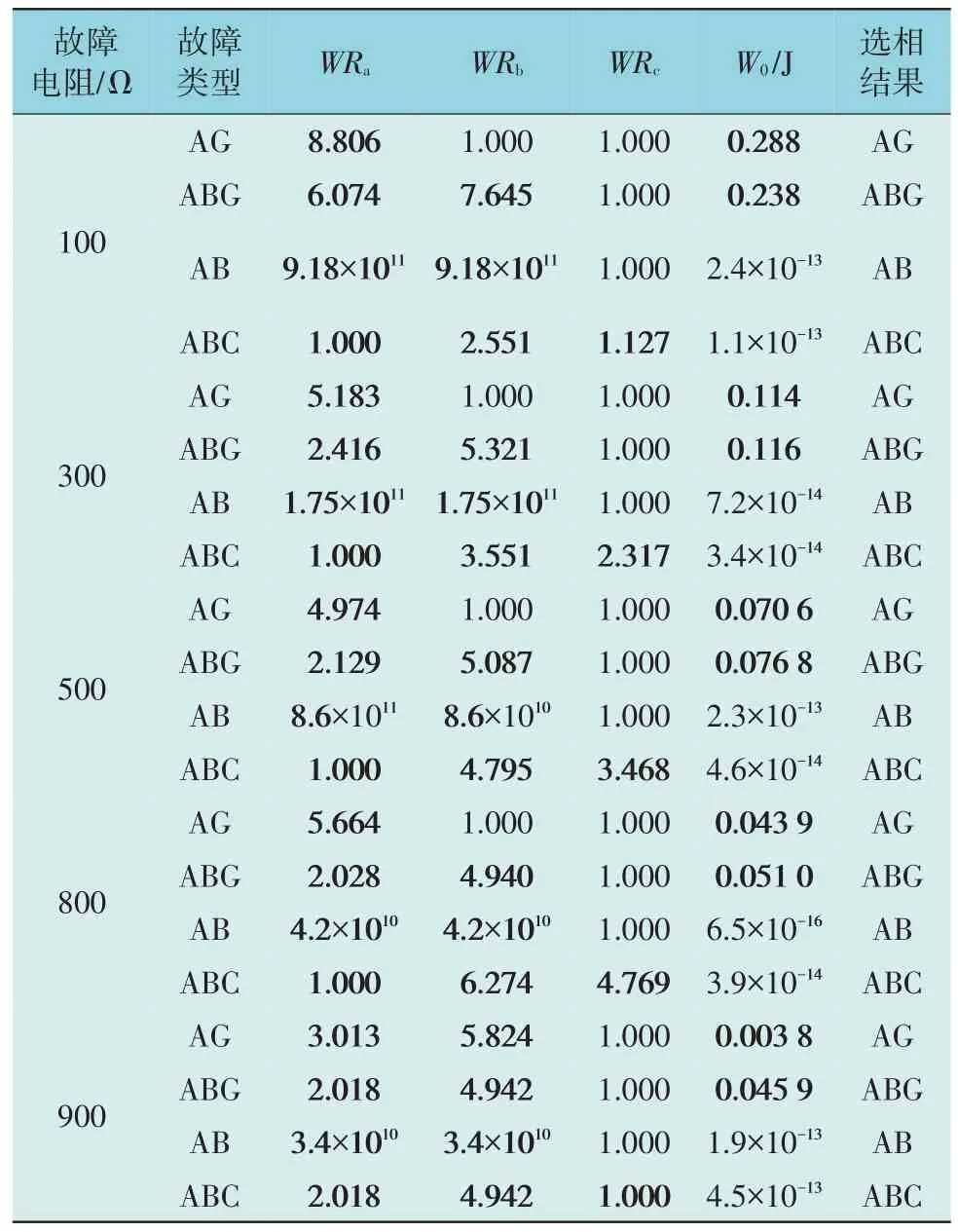
表2 基于不同过渡电阻的各种故障情况的下的选相结果Table 2 Phase selection results under various fault conditions based on different transition resistances

3.4 不同故障位置的仿真

在距离P侧10 km、150 km、290 km 3 个位置，即K1，K2，K3 点，设置10 种类型金属性短路故障，故障开始时间均设置为1 s，限于篇幅，仅列出了AG，ABG，AB，ABC 4 种典型故障类型的仿真结果如表3 所示。由表3 可知，本文所提选相方案不受故障点位置的影响，线路上不同位置故障均可准确选相。

表3 不同故障位置下的选相结果Table 3 Phase selection results under different fault locations

3.5 不同故障初相角仿真

以线路P侧A 相电压相角为参考，在K1，K2，K3 点发生各种类型金属性接地故障情况下，通过设置不同的故障发生时刻，模拟在0°，36°，54°，90°等不同故障初相角下选相方法的选相性能。K3 点在不同故障初相角下的故障选相结果如表4 所示。由表4 可知，本文方法同样不受故障初相角的影响，能够准确实现不同故障初始角下的故障选相。

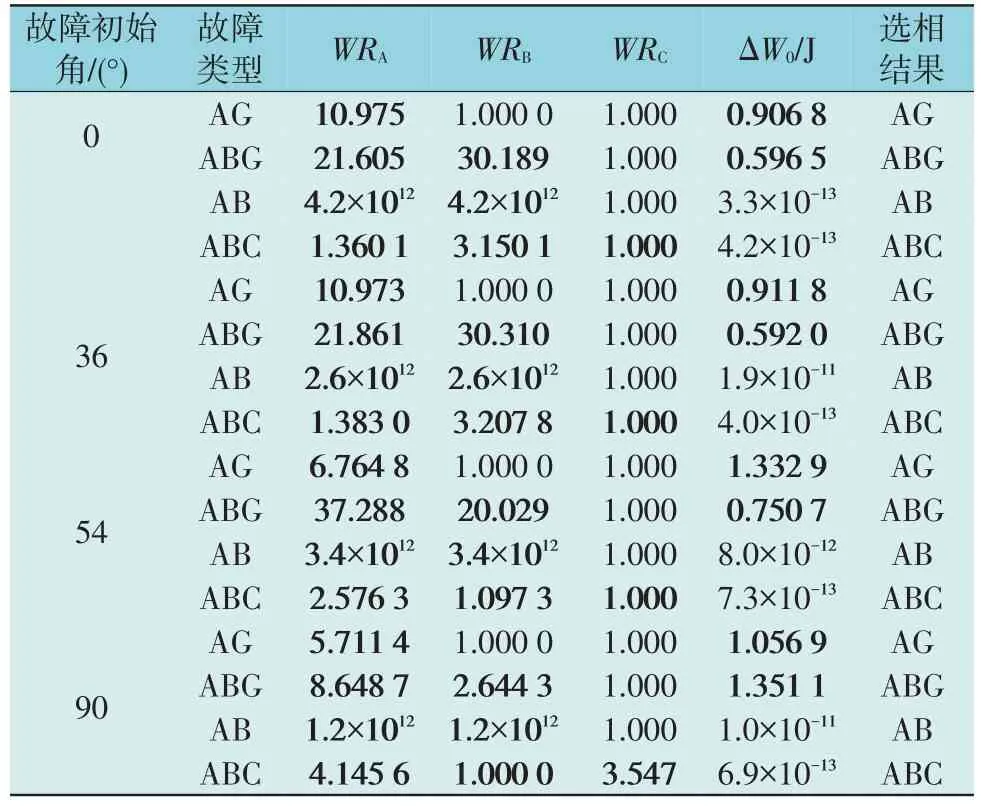
表4 不同故障初相角下的故障选相结果Table 4 Phase selection results under different fault initial phase angles

3.6 弱电源侧故障仿真

针对弱电源侧基于电流突变量的故障选相方法存在选相灵敏度不足的问题[8]，通过设置典型工况对本文所提方法进行适应性验证分析。将P侧电源容量减小至原容量的1/100，此时P侧对Q侧而言可视为弱电源侧。在此情况下分别进行不同故障类型、不同故障位置、不同初相角、不同过渡电阻下的仿真。

限于篇幅，仅列出弱电源情况下K3 点在故障初始角为36°和54°时发生表1 中所有金属性故障的选相结果，如表5 所示。

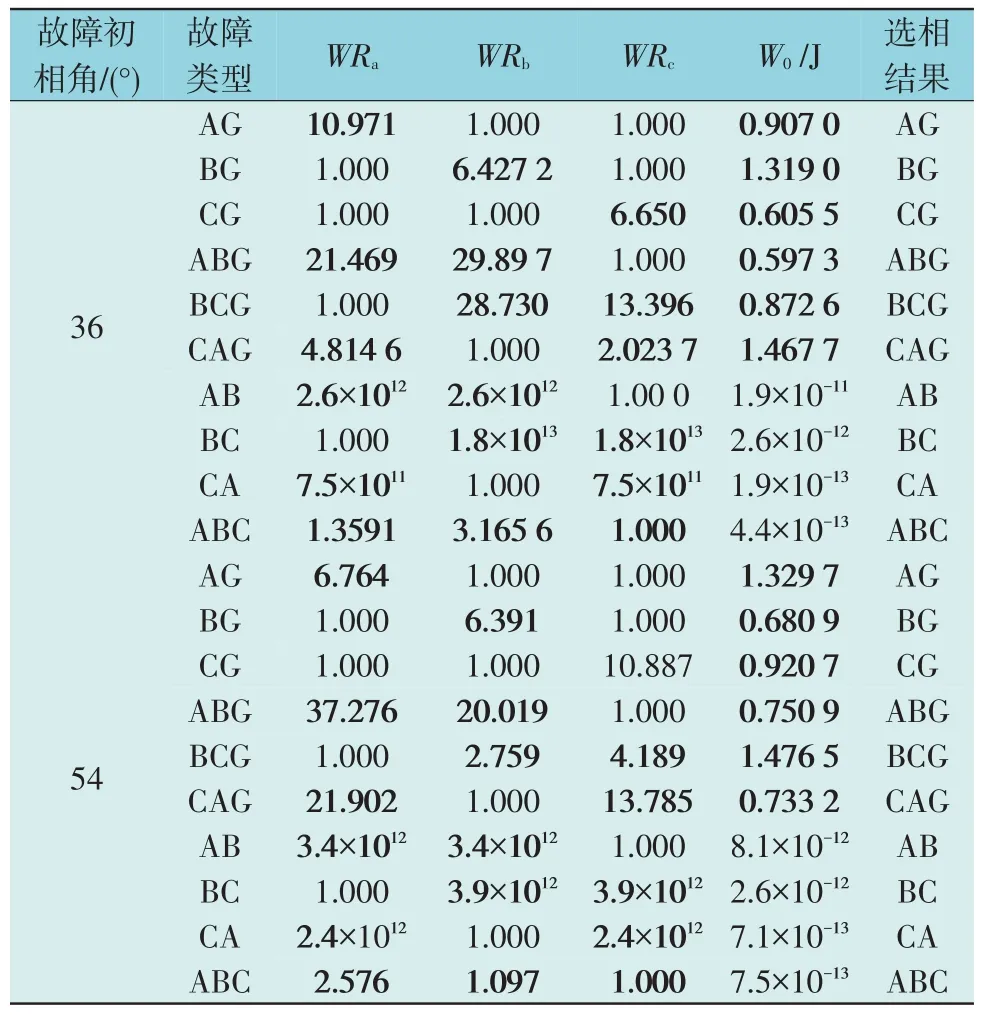
表5 弱电源侧故障选相结果Table 5 Phase selection results at weak power supply side

由表5 可知，本文所提方法在弱电源侧故障时同样具有准确选相的能力；对比表5 和表4 中故障初始角36°和54°对应数据可见，在弱电源侧故障情况下本文选相方法同样不受故障初相角的影响。

4 结论

本文利用电压和电流故障分量构建三相暂态能量比和零序暂态能量，并与各自设定的阈值比较以实现故障选相。通过动模试验故障录波数据和PSCAD/EMTDC 仿真数据的分析，验证了选相方法的可靠性和适用性。结论如下：

1）综合利用故障前后1/4 周波电压、电流故障分量绝对值计算三相和零序暂态能量；将三相暂态能量同除以三者中的最小值以构建暂态能量比，结合零序暂态能量与各自设定的阈值比较，实现故障选相。

2）仿真结果表明，本文方法同样不受故障位置、故障初相角及弱电源侧故障的影响，且耐受过渡电阻能力较强，可正确选相经800 Ω以下过渡电阻故障，且不会出现三相故障误选相为两相短路接地，理论上可实现各种故障类型的识别。

本文研究中，不同类型故障时三相和零序暂态能量随时间变化的特征明显，基于此特征能否定位满足选相判据的初始时刻，即在保证可靠性的同时进一步提高选相快速性，将是后续的研究工作。