大跨径斜拉桥拉索施工控制研究
刘占兵,胡 凯,宗 伟
(1.湖北省建设投资集团有限公司/湖北省路桥集团有限公司,湖北 武汉 430000;2.湖北交通职业技术学院,湖北 武汉 430000)
1 引 言
武穴长江公路大桥主桥桥型方案为主跨808 m双塔斜拉桥,双塔双索面半漂浮体系,钻石型索塔,空间扇形斜拉索。桥跨(主桥、滩桥)组合为:(56+100+56)m连续箱梁+(6×30)m预应力混凝土连续T梁+(56+100+56)m连续箱梁+(80+290+808+75+75+75)mPK钢箱混合梁斜拉桥+40 m简支混凝土梁,桥梁全长2 051.5 m,其中主桥斜拉桥长1 403 m(不含桥台)。
大跨径斜拉桥的施工控制理论主要有无应力状态法(提出了结构的基本原理)、几何控制法(强调了索长、线形等几何要素的控制)和自适应控制法(收集索、梁、塔等构件在制造、安装等过程的实际数据用于模型修正,从而有针对性、有准备地进行过程控制)等。
斜拉索无应力长度是控制主梁整体线形的主要参数之一,可通过无应力索长的调整实现主梁整体线形、索力、塔偏等其他结构参数的控制,由于每一根索的无应力长度都是独立变量,不会相互干扰,且长度的测量精度高,因此将无应力索长作为大跨径斜拉桥的基本控制变量具有理论和实践的一致性。
针对武穴长江公路大桥的结构体系特点,采用弹性悬链线理论精确解实用迭代方法计算无应力索长,提出大跨径斜拉桥拉索施工控制方法,该计算方法在大跨径斜拉桥施工控制效果良好。
2 斜拉索控制参数计算总体流程
由于斜拉索施工阶段多,受力状态复杂,影响因素多,要实现设计成桥状态,必须选择合适的斜拉索控制计算总体流程,针对不同施工阶段进行计算,确定斜拉索施工控制参数。
具体步骤为:(1)根据设计图纸得到成桥状态无应力索长L0;(2)根据施工方案,建立各施工阶段模型,得到主跨合龙前最大悬臂状态无应力索长L1;(3)将L0,L1代入各施工阶段进行计算,通过迭代得到满足设计成桥状态施工控制参数。
在桥梁施工过程中收集实际参数,对模型进行修正,并重新计算施工控制参数。
3 斜拉索施工控制
对武穴长江公路大桥无应力索长进行研究,采用弹性悬链线理论精确解实用迭代计算方法计算无应力索长。
3.1 应力索长的弹性悬链线理论精确解实用迭代计算方法
建立如图1(a)拉索上模型,梁端锚点为I端,坐标(0,0)和塔端锚点l端坐标(l,I)。拉索索力为T,其水平分力为H,其竖向分力为V,N为索力T在拉索弦线上的分力,E为拉索弹性模量,A为拉索截面面积,q为拉索单位长度质量。
假设变形前单位长度重量为q0,变形后单位长度重量q,s为成桥状态的拉索索长;s0为拉索无应力索长。由于拉索变形前后的总重不变,可以得到
q0ds0=qds
(1)
根据胡克定律
ds0[1/(1+T/EA)]ds
(2)
则
q/q0=ds0/dx=1/(1+T/EA)
(3)


图1 斜拉索计算模型示意图
定义参数u=u(x),其双曲正弦值等于拉索任一点的斜率,且dy/dx=sinh(u)=tan(α),α为拉索任一点的倾角。
根据微段的静力平衡条件有
∑x=0d(Tdx/ds)=0
(4)
∑y=0d(Tdy/ds)-qds=0
(5)
由式(4)可以看出,微段索力水平分力H相等。
(6)
由式(6)积分可得
(7)
(8)
(9)
(10)
由ds/dx=cosh(u)=T/H,得到变形后索长s
(11)
式(11)为弹性悬链线理论拉索变形后的索长公式。
根据式(11)可知,求得u(l)就可求得拉索索长。
对式(2)积分可以得到
(12)
将x=0处边界条件u(x)=u(0),=0代入式(12)
(13)
得:
则无应力索长s0为
(14)
因此,计算得到u(0)和u(l)u就可以精确求得无应力索长s0。
引入x=l处边界条件:u(x)=u(l),x=1,y=h,代
入式(8)和式(10)可得
(15)
(16)
假定u(0)和u(l)u为未知待求参数,式(15)和式(16)为非线性方程组,需要通过迭代求解。
3.2 武穴长江公路大桥斜拉索的制造索长
制造索长考虑了索塔锚固点定位及定位时温度修正、新增锚垫板、健康监测锚索计、上塔柱预抬、南边跨预偏等因素,修正索长,给出锚垫板间无应力索长。均在设计基准温度为15 ℃条件下给出。
为充分考虑施工误差的影响,武穴桥制造索长分五批给出,限于篇幅,部分索长见表1、表2。
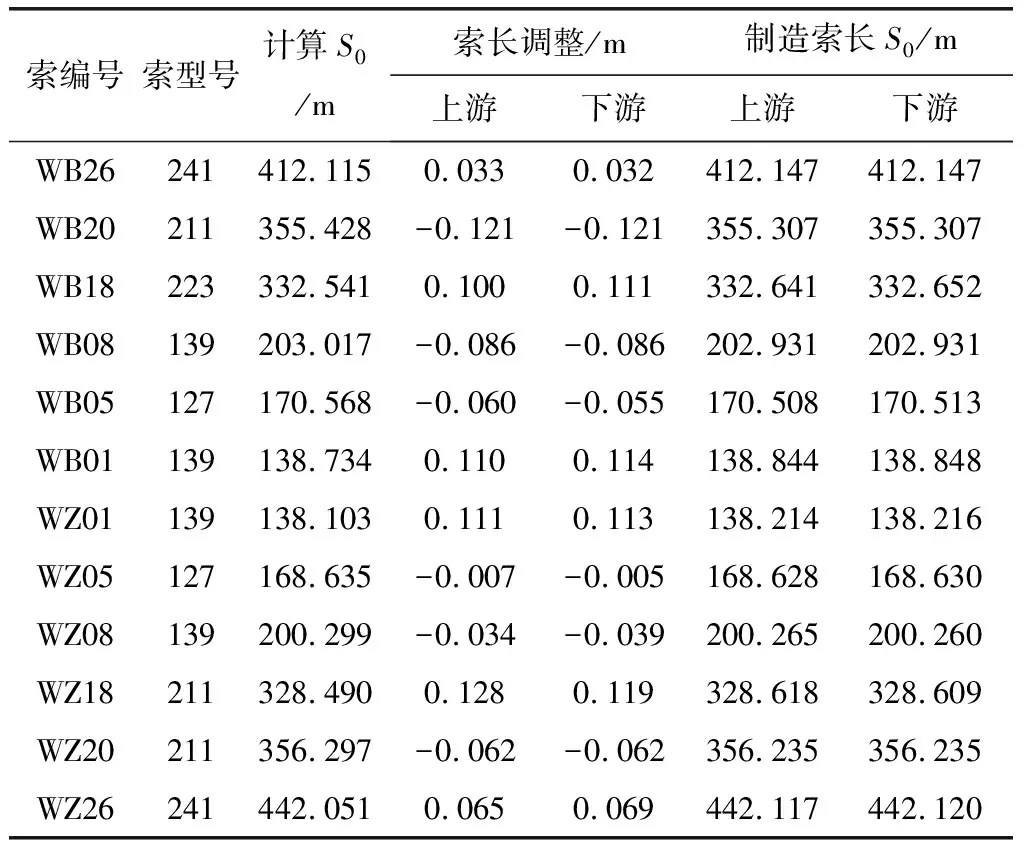
表1 北塔斜拉索部分制造索长

表2 南塔斜拉索部分制造索长
3.3 成品索弹模测试
斜拉索制造单位进行了成品索弹模测试,见表3。测试结果表明成品索弹模符合规范要求,且数值较为集中。结合其他斜拉桥弹模测试结果,本桥采用斜拉索弹模为197 GPa。
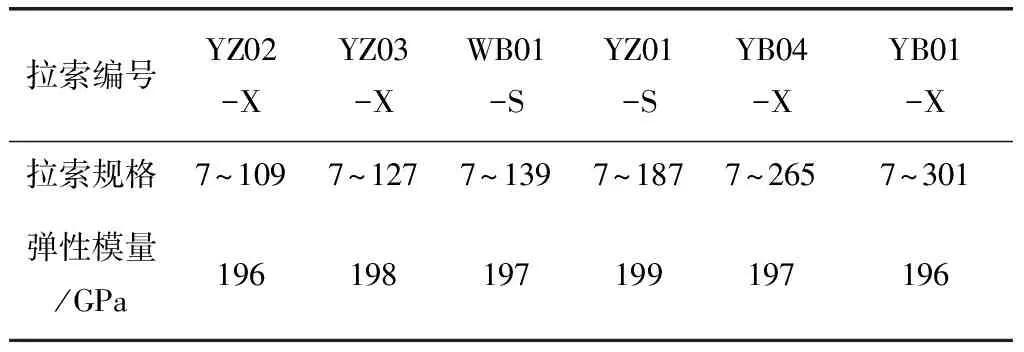
表3 成品索弹模测试结果
3.4 斜拉索张拉控制
斜拉索张拉控制理论分析中,北塔斜拉索、南塔中跨斜拉索、南塔边跨1#~10#索索长均采用一次张拉至设计索长,11#~26#索考虑合龙后二次调索,以避免南塔在施工过程中塔偏过大、塔梁限位支反力过大的不利影响。斜拉索初张拉采用张拉力控制,其余张拉均采用拔出量控制。
施工期中,南、北两侧主梁均架设至17#节段时,长江水位超过警戒水位,主梁架设施工被迫停止。利用停工期进行施工期调索,消除目前为止的线形误差、索力误差等结构误差,从而以较好的结构状态进入后续施工,节省合龙后调索工作量。考虑到北塔竖向钢绞线索临时限位的作用,北塔调整17#~5#斜拉索;南塔斜拉索全部调整。
以北塔为例,调索后测量结果表明:南北三个悬臂线形平顺,悬臂前端高程偏高约5~7 cm,斜拉索索力整体偏差较小,结构应力水平正常,为后续施工控制提供了较好的结构状态条件。
成桥索力测试,北塔斜拉索及南中跨斜拉索的索力偏差最大7.8%;全部满足施工监控方案中的监控目标要求;南边跨斜拉索索力偏差超过5%仅3根,最大为5.7%,其余均满足施工监控方案中的监控目标要求。上下游索力差均小于3%。总体而言,斜拉索索力控制是成功的。
4 结 语
大跨径斜拉桥施工控制计算应面向施工,兼顾结构设计特点、具体施工方法、测试测量方法及误差控制手段等方面,在确保过程安全可控的前提下及允许误差范围内达到设计成桥状态,核心是几何控制。无应力索长是独立变量,采用以锚杯可调量为约束的索长调整量联系各施工阶段,便于指导以锚杯拔出量控制的实际斜拉索张拉施工。将调索分为成桥状态、最大悬臂状态、全部施工阶段3个步骤,依次逐步确定斜拉桥各状态参数,概念清晰;方便与设计、施工等各方就计算结果进行对接,也反映了随着现场施工推进而不断深入的特点。具体调索计算过程采取先调整塔偏位移、再调整主跨线形、最后调整索力均匀性与桥塔剪力的思路符合大跨径斜拉桥结构特点;采用本文方法武穴长江公路大桥施工过程结果与实测值一致,调索完毕后索力、主梁线形、桥塔偏位误差均在允许误差范围内。

