CDMA+FDMA非差非组合区域PPP-RTK
侯鹏宇,张宝成,刘 腾,查九平
1.中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,湖北 武汉 430071;2.中国科学院大学地球与行星科学学院,北京 100049
GNSS现已步入多星座、多频点时代,多频多模数据将为用户提供更精准可靠的导航、定位和授时服务[1-3]。美国的GPS正逐步实现现代化,除以往的L1和L2信号外,又增加了L5信号。我国自主研制的北斗导航卫星系统(BDS)在2020年7月31日实现全球组网,完成了BDS-3建设,将在一段时间内与BDS-2并存,向全球用户提供服务。BDS-2向用户播发B1I、B2I和B3I三频观测值,BDS-3继承了BDS-2的B1I和B3I信号,同时播发B1C、B2a和B2b信号[4-6]。欧盟的Galileo系统当前有22颗卫星可用,播发E1、E5a、E5b、E5和E6五频信号。不同于上述3大码分多址(CDMA)系统,俄罗斯的GLONASS系统采用频分多址(FDMA)信号体制,播发双频观测值。GLONASS也开启了现代化进程,设计了第三频率CDMA信号,但在未来较长时间内仍主要以FDMA双频信号提供服务。
PPP-RTK是当前最前沿的GNSS精密定位技术,它继承了精密单点定位(PPP)灵活的单测站作业模式,同时融合了实时动态定位(RTK)固定模糊度的思想,最终实现快速精密定位[7-8]。PPP-RTK相对于PPP的创新突破在于,除卫星轨道和钟差等精密产品外,还额外提供卫星相位偏差(SPB,也称UPD)产品[8]。用户单向自主获取SPB等精密产品,能同RTK一样恢复模糊度的整数特性,由此缩短定位初始化时间,实现单测站快速高精度定位。国内外众多学者提出了多种PPP-RTK算法,主要包括UPD/FCB[9]、整数恢复钟[10]、解耦钟[11]和非差非组合方法[12]。前3种方法在提出之初均基于消电离层组合模型,而非差非组合方法直接从原始观测值出发,更利于多频多模数据处理[13-14]。同样为了灵活处理多频多模数据,前3种方法也探索了非差非组合数据处理模式[15-17]。
基于非差非组合数据处理理论,针对CDMA系统的PPP-RTK研究较多[18-20],而GLONASS FDMA系统由于频率间偏差(IFB)的影响难以实现PPP-RTK技术。PPP-RTK的核心思想在于如何恢复模糊度的整数特性,CDMA PPP-RTK借助SPB产品带有的参考站基准模糊度,在用户方程的参数域构建了整数可估双差模糊度。然而,由于GLONASS采用FDMA信号体制,同一时刻跟踪到的卫星频率不同,由此产生的IFB导致无法形成双差模糊度进行固定。早期研究通过额外施加电离层约束或者选择两颗参考星构建了具备整数特性的可估模糊度,并尝试了模糊度固定[21-22]。最新研究却指出,严密的模糊度固定不仅要保证可估的线性组合模糊度的整数特性,还要确保其原始模糊度不丧失整数特性。根据这一指导思想,文献[23]提出了GLONASS整数可估理论;文献[24—25]将其应用于RTK定位,实现了快速模糊度固定。
本文将整数可估理论拓展应用至PPP-RTK,提出了一种CDMA+FDMA多系统非差非组合区域模型。首先从CDMA系统出发,通过施加站间单差电离层约束构建了服务端和用户端PPP-RTK模型。构建FDMA PPP-RTK模型时,先选取与CDMA模型相同的基准,再将可估模糊度转换成整数可估模糊度,以此保证模糊度固定的严密性。建立FDMA PPP-RTK模型的关键是如何利用整数可估理论计算模糊度的设计矩阵,与CDMA系统不同,其设计矩阵并非对角矩阵,而是下三角矩阵,需逐次确定各元素。由于两类信号体制的系统均采用相同基准构建模型,其方程结构一致,仅模糊度的系数矩阵存在差异,最终构建了能融合处理CDMA+FDMA多频多模观测值的PPP-RTK统一模型。为了评估模型的性能,采集了香港连续运行参考网的GPS/BDS/Galileo/GLONASS数据进行PPP-RTK服务端产品估计和用户端仿动态定位试验。最后,对试验结果进行分析、讨论并对全文进行总结。
1 方 法
从GNSS非差非组合观测方程出发,本节分别推导了CDMA和FDMA 区域PPP-RTK模型。
1.1 GNSS非差非组合观测方程
将接收机r(r=1,2,…,n)跟踪到卫星s(s=1,2,…,m)发射的频率j(j=1,2,…,f)的信号的伪距和相位观测方程表示为[2]
(1)
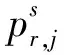
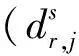
1.2 CDMA非差非组合区域PPP-RTK模型
首先考虑CDMA系统,针对区域参考网,分别推导服务端和用户端模型。在服务端,除GNSS观测方程式(1)外,再额外引入站间单差电离层加权约束[26]
(2)
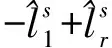
联合方程式(1)、式(2),其系数矩阵列向量存在线性相关,参数无法独立求解,即方程秩亏。为便于辨识和消除秩亏,当j=1,2时,将接收机和卫星伪距偏差分离为如下形式
(3)
式中,消电离层组合和几何无关组合接收机伪距偏差分别为
(4)
(5)
式中
(6)
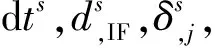
(7)
式中,重组参数表达式为
(8)
可见,由于增加了站间单差电离层约束,测站r的可估电离层斜延迟吸收的是测站1的几何无关组合接收机伪距偏差,而不是测站r的几何无关组合接收机伪距偏差。
(9)
式中
(10)
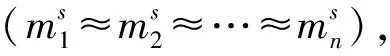
(11)
式中
(12)
可见,模糊度以双差形式整数可估,可实现模糊度固定。

(13)
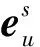
最后,总结额外引入站间单差电离层约束带来的两点好处:①增加了多余观测信息,提高了模型强度;②由式(8)可知,服务端每个测站估计的电离层延迟均包含测站1的接收机伪距偏差,基准统一,可直接对服务端估计的电离层延迟进行插值供用户改正。
1.3 FDMA非差非组合区域PPP-RTK模型
同样先推导服务端函数模型,借鉴CDMA推导思路,选取同样的基准,但顾及GLONASS IFB,对比方程式(11),可得FDMA方程为
(14)
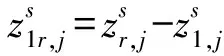
严密来讲,由于GLONASS IFB的影响,重组的接收机钟差、伪距和相位偏差均应带有卫星标识。但由此会导致估计参数众多,引起额外秩亏,需要将所有模糊度选为基准,致使无法实现模糊度固定。好在上述几类参数均是相对于测站1的相对量,已有研究表明,同款接收机(指接收机、天线、其余固件均一致)的站间单差GLONASS IFB在大多数情况下可以忽略[29]。因此,上述参数在方程式(14)中退化为卫星无关量,意味着该模型仅适用于同款接收机的参考网。
GLONASS IFB影响了模糊度参数的重组,方程式(14)并未形成可估的双差模糊度,而是两个单差模糊度。将两个单差模糊度进行线性组合,构成如下可估方程[23]
(15)
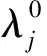
(16)
为GLONASS可估模糊度。

(17)
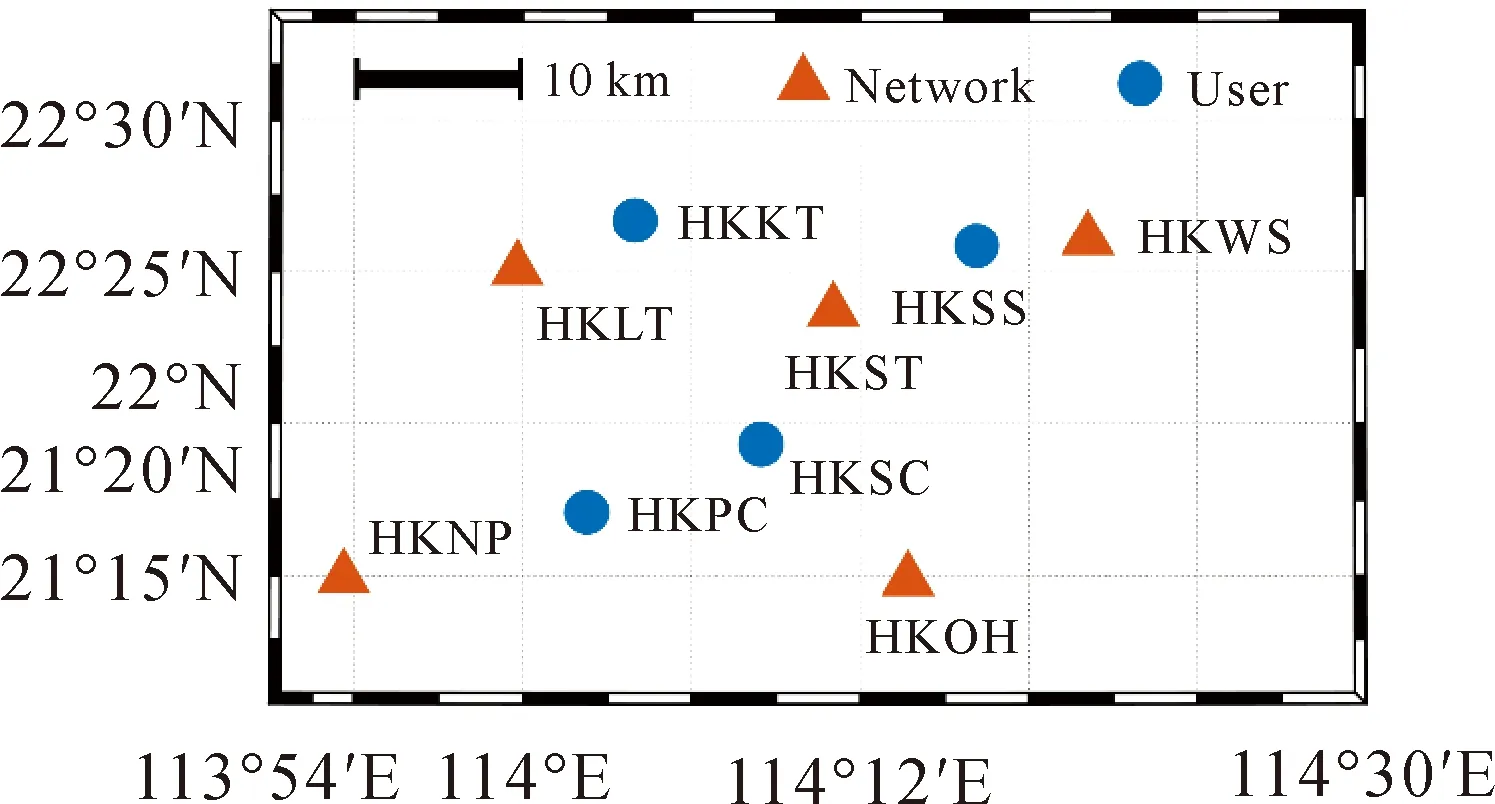
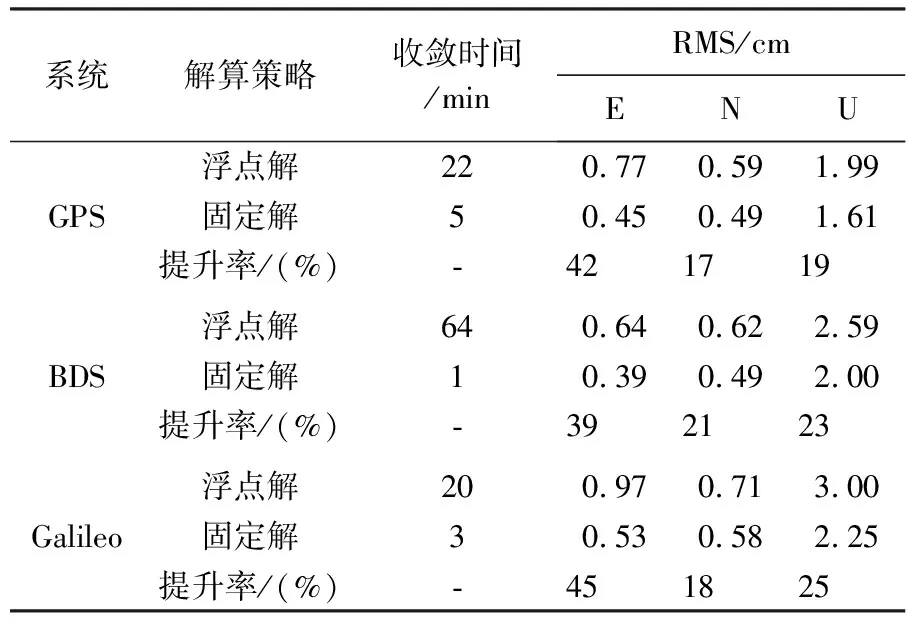
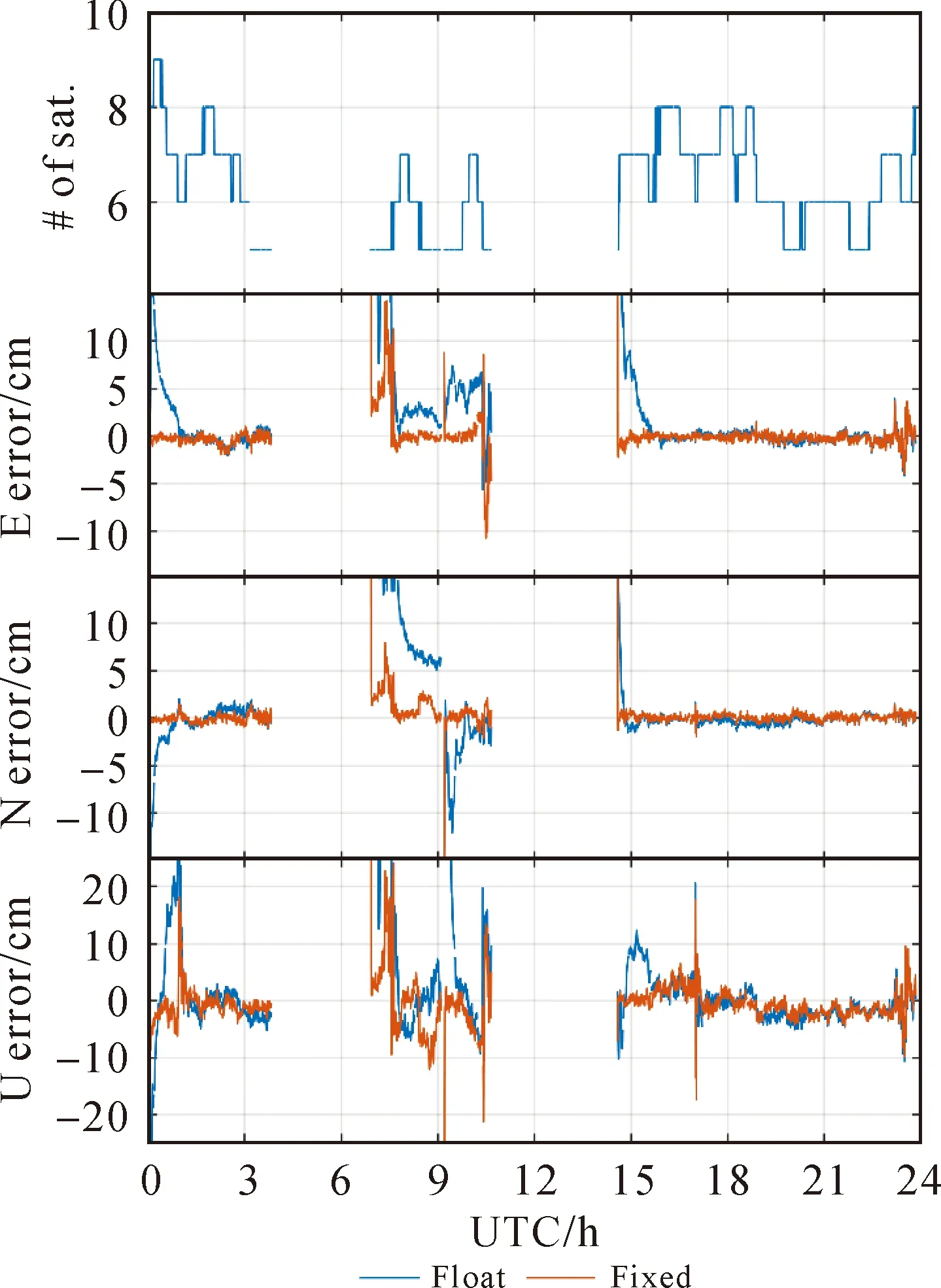
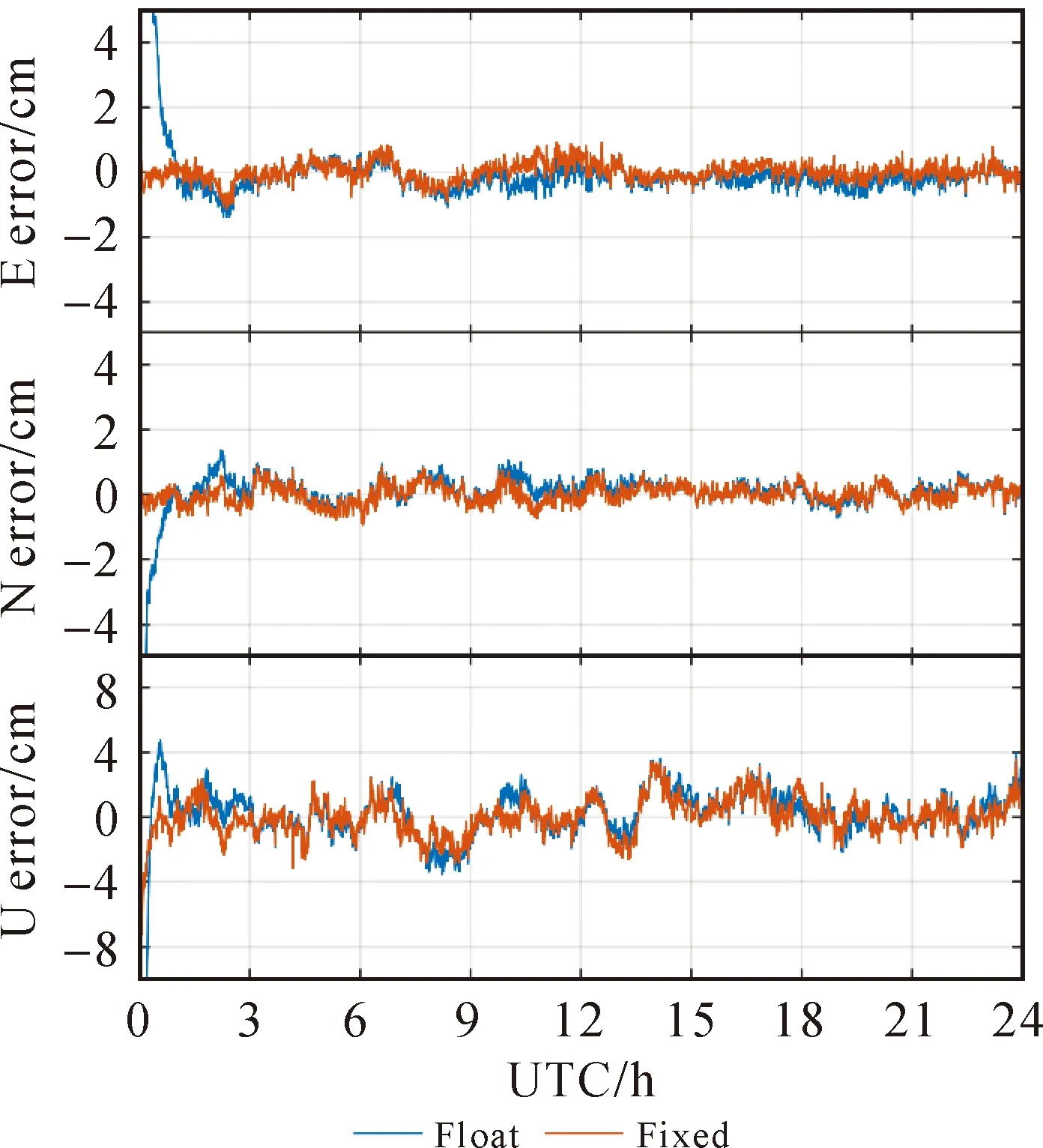
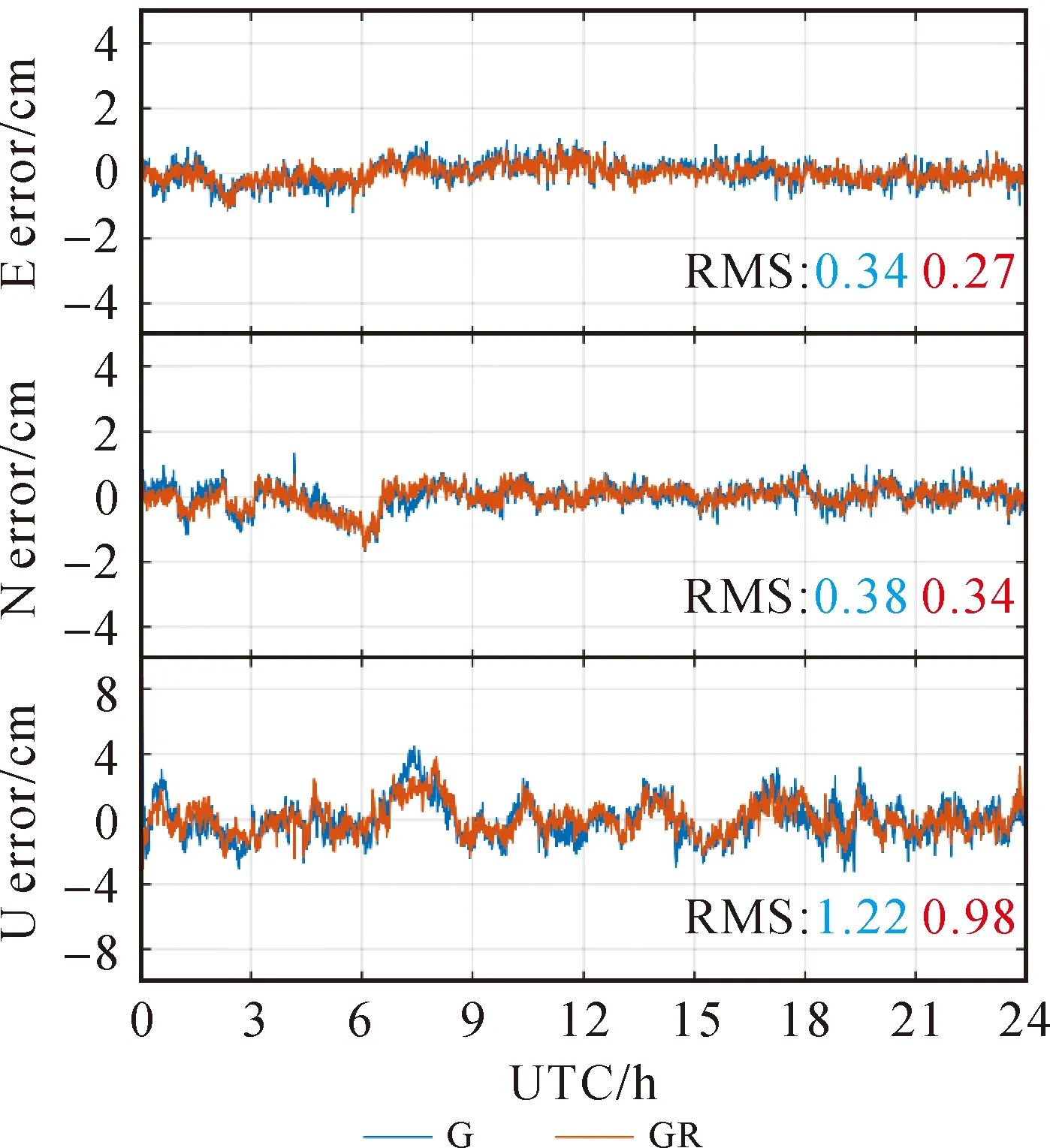
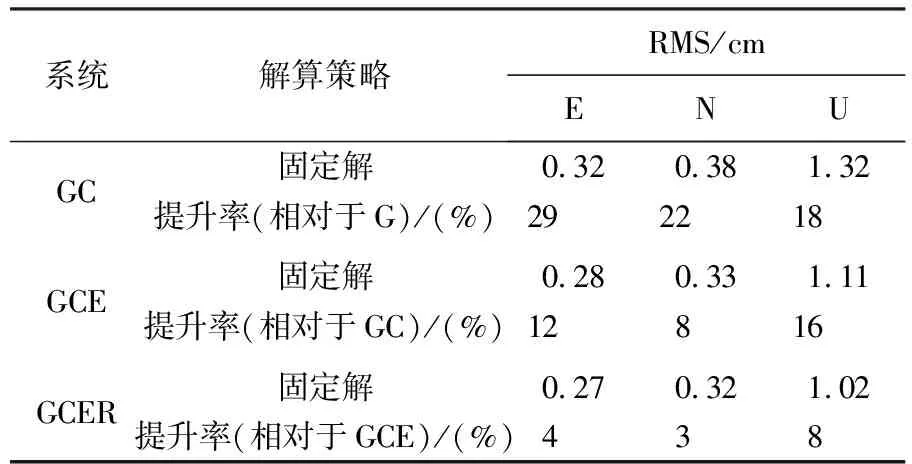
式中,a1(i+1)=ai+1-a1。整数α和β由方程式-αiai+1+βigi=gi+1确定,g1=a1,gi=GCD(a1,a2,…,ai)(1 (18) 虽然式(18)中整数可估模糊度的解析形式十分复杂,但在构建模型时,实际上只需要关注其设计矩阵L。区别于CDMA系统的设计矩阵,L并非对角阵,而是一个下三角矩阵,它决定了GLONASS模糊度固定的性能。模糊度固定性能可用ADOP值表征,ADOP越小,则模糊度固定成功率越高。文献[23]表明,双频FDMA系统ADOP值与CDMA系统ADOP值之间的关系可近似为 (19) 可见,GLONASS模糊度固定严重依赖于可视卫星数,以7颗卫星为例,GLONASS ADOP值大约是GPS ADOP值的3.5倍,意味着GLONASS模糊度固定的确比GPS困难,但是随着滤波进行,依然可成功固定。更值得一提的是,由于L的特殊形式,GLONASS ADOP值主要被L矩阵的第一个对角线元素放大,因此,若进行部分模糊度固定,即每个频率最多固定m-2个模糊度,而不是m-1个模糊度,可显著提高模糊度固定成功率。此时,GLONASS模糊度固定成功率几乎接近CDMA系统[23]。 至此,推导了GLONASS FDMA服务端PPP-RTK函数模型。用户端可估函数模型与服务端基准一致,写为 (20) 为实现GLONASS PPP-RTK,假设站间单差IFB可忽略,构建了满秩函数模型,该模型仅适用于同款接收机的参考网。当CDMA和FDMA数据联合处理时,只需要组合两类模型的方程,联立求解即可。由此,构建起了CDMA+FDMA多系统融合PPP-RTK统一模型。 本节首先介绍了试验数据和处理方法,然后评估了服务端产品质量,最后分析了用户端定位性能。 选取香港连续运行参考网中9个装备Leica GR50接收机和Leica25.R4天线的测站进行试验。图1展示了9个测站的位置分布,其中5个参考站(站间距<35 km)用于服务端产品估计,4个用户站用于定位性能评估。采集了2021年1月2日至2021年1月4日3 d的GPS/BDS/Galileo/GLONASS数据进行处理,除Galileo观测值为三频,其余均为双频,数据采样率为30 s。由于该参考网的接收机尚未升级,仅跟踪到BDS-2观测值,无BDS-3观测值。 图1 选自香港连续运行参考网中9个测站的分布 用户端的随机模型和动态模型与服务端保持一致,增加的位置参数按时变处理,进行仿动态定位测试。采用LAMBDA[31]进行部分模糊度固定。 本节将首先分析四系统各项产品的估值及其精度,然后给出组合产品的精度,最后说明服务端产品的性能评估不仅需要分析某一项产品的精度,更重要的是分析组合产品的精度。 图2展示了四系统SPB估值及其精度(STD)。可以看出,各个系统的SPB均在滤波收敛后趋于稳定。观察其精度,在滤波收敛后,STD可达0.2周。然而,这仍然高于相位观测值毫米级的精度,这是否意味着估计的SPB不具备改正高精度相位观测值的能力?此外,当卫星刚升起时,SPB估值精度甚至超过1周,这是否意味着这一时期的SPB无法用于用户改正?实际上,两个问题的答案都是否定的,本文将在展示完其余产品后,解释这一问题。 图2 四系统卫星相位偏差(SPB)估值及其精度(STD) 当用户使用Galileo三频观测值进行定位时,除SPB外,还需要利用卫星伪距偏差(SCB)改正信息。图3展示了Galileo第三频率SCB及其估值精度。观察各段SCB时间序列,基本也是在收敛后趋于稳定。其精度虽然能在收敛后达到厘米级,但在初始化阶段精度较低。 图3 Galileo第三频率E5b卫星伪距偏差(SCB)及其精度(STD) 图4展示了测站HKST四系统斜电离层延迟的估值及其STD。各系统的斜电离层延迟均在UTC=6时左右达到最大值,即当地时间14点,符合电离层延迟的时变特性。估计得到的斜向电离层延迟存在负值,这是由于可估的斜向电离层延迟吸收了偏差参数。4个系统的斜电离层延迟估值精度STD最终收敛至2 cm左右,难以达到毫米级的精度,初始化时段精度更差。 图4 测站HKST四系统斜电离层延迟估值及其精度 如前所述,独立评估各类产品的精度均难以达到相位观测值毫米级的精度。实际上,各类产品高度相关,比如钟差和SPB,SPB和电离层,均高度相关[32]。因此,不能孤立地评估各类产品的精度,而要评估组合产品的精度。这也更符合实际的应用场景,因为用户端并不是仅改正某类产品,而是组合多类产品进行改正。图5展示了组合卫星钟差、SPB和斜电离层的估值精度。这里组合产品的STD根据服务端输出的方差协方差矩阵,通过误差传播定律求得。可见,STD时间序列在大部分时刻均处于毫米级精度,其起伏变化是卫星高度角变化所致。因此,服务端估计得到的产品精度能满足高精度用户定位要求,即使是卫星刚升起阶段。 图5 四系统组合卫星钟差、卫星相位偏差和电离层的精度(STD) 由图2—图5可知,由于产品之间高度相关,孤立评估每类产品的精度意义不大,因此本文省略了对钟差产品的独立评估,而是在图5展示了组合钟差、SPB和电离层产品的精度。与UPD/FCB等PPP-RTK方法不同,本文方法并没有使用全球网估计的卫星钟差和卫星相位偏差产品,而是在区域网中将两类产品与大气延迟同步估计。该方法的优势在于服务端同步估计各类参数,得到的产品完全自洽,组合产品精度可达毫米级,用户端进行综合改正,最终实现快速高精度定位。 本节首先分析CDMA单系统模糊度固定和PPP-RTK定位,然后分析FDMA模糊度固定和PPP-RTK定位,最后给出CDMA+FDMA多系统定位结果。 图6展示了测站HKSC 1月4日在东方向上GPS、BDS和Galileo浮点解和固定解的定位结果。3个系统均能在几分钟内实现模糊度固定,定位误差收敛至2 cm以内。反观浮点解,其收敛时间较长,且在收敛后稳定性也不如固定解,这体现了模糊度固定不仅能加快收敛,同时还能在一定程度上提高定位精度。对比3个系统的误差曲线,发现BDS系统的定位噪声略小于另外两个系统,这得益于BDS系统在亚太地区分布广泛的GEO和IGSO卫星。 图6 测站HKSC的GPS/BDS/Galileo单系统模糊度固定解和浮点解在东方向定位误差 为进一步分析CDMA单系统定位性能,表1统计了3 d内所有测站的平均模糊度首次固定时间(time-to-first-fix,TTFF)、收敛时间及3个方向的RMS。TTFF针对于固定解,其定义为模糊度固定通过ratio检验(阈值为2),且定位误差收敛至水平2 cm,高程5 cm并至少保持20个历元。浮点解的收敛阈值放宽至水平4 cm,高程8 cm。即使这样,固定解TTFF也显著小于浮点解收敛时间。例如,GPS浮点解需要22 min才收敛,而固定解TTFF为5 min。BDS系统浮点解的收敛速度比其他两个系统慢,这是由于北斗GEO卫星几乎处于静止状态,几何机构几乎不变[33]。然而,通过模糊度固定,BDS系统定位收敛速度显著提高,能在1 min内收敛,这才真正发挥了北斗可观测卫星数目多的优势。分析各系统定位RMS可以发现,模糊度固定还能提高定位精度,尤其是在东方向,可实现40%左右的提升。 表1 GPS/BDS/Galileo单系统定位平均收敛时间与RMS 下面分析GLONASS FDMA系统的模糊度固定能力和PPP-RTK定位性能。图7展示了HKSS测站GLONASS单系统定位结果。对比浮点解和固定解,可发现模糊度固定带来了显著增益。当GLONASS卫星数为6颗及以上时,可在几个历元内实现快速模糊度固定。当可视卫星为5颗时(UTC 7点至11点),模糊度首次固定时间变长,定位效果变差。图7中无结果部分为卫星数不足5颗,此时设计矩阵结构差,可能出现数值计算问题,难以成功固定模糊度,未进行定位解算。总的来看,GLONASS模糊度固定高度依赖于卫星数目,这与本文在方法部分的理论推导符合。 图7 测站HKSS的GLONASS单系统模糊度固定解和浮点解定位误差以及对应的卫星数目 为进一步说明GLONASS模糊度固定带来的好处,本文组合GLONASS和GPS,但只固定GLONASS模糊度,而GPS模糊度保持其浮点形式。如图8所示,仅固定GLONASS模糊度实现了快速收敛,而浮点解定位误差需要较长时间才能收敛至厘米级水平,这证明了GLONASS整数可估PPP-RTK模型保证了模糊度固定的严密性,固定GLONASS模糊度能带来定位性能的提高。 图8 测站HKSS的GPS+GLONASS但只固定GLONASS模糊度的固定解与浮点解定位误差 为突出GLONASS在实际应用中的价值,图9对比了GPS+GLONASS和GPS单系统模糊度固定解的定位性能,这里双系统定位所有模糊度均尝试固定,以符合实际应用的解算策略。结果表明,双系统的误差曲线基本在单系统的误差曲线内波动,定位精度有一定程度的提升。此外,双系统定位实现了模糊度瞬时固定,即部分模糊度在首历元成功固定并带来有效增益。 图9 测站HKSS的GLONASS+GPS双系统与GPS单系统定位误差 为定量描述加入GLONASS观测值的贡献,表2统计了所有测站3 d定位结果的RMS平均值及其相对于GPS单系统的提升率。对比表1中GPS单系统的定位RMS,双系统定位精度有所提高,东、北、天(E/N/U)3个方向提升率分别为9%、12%和14%。 表2 GPS+GLONASS(GR)定位平均RMS及其相对于GPS(G)单系统的定位提升 最后,给出CDMA+FDMA多系统融合定位的结果。图10展示了测站HKPC 1月4日的单系统、双系统、三系统和四系统定位结果,图下方数值为定位误差RMS。对比GPS+BDS双系统与GPS单系统的定位误差曲线,双系统定位误差显著减小,进一步加入Galileo观测值,定位误差再次小幅减小,再加入GLONASS观测值,定位精度仍有小幅提升。这证明了各个系统的定位贡献,也证明了GLONASS基于整数可估模型实现严密模糊度固定之后,在三系统的基础上加入GLONASS仍有增益。 图10 测站HKPC的单/双/三/四系统定位误差 为进一步证实上述结论并定量描述定位性能提升,表3统计了所有测站3 d的多系统定位RMS以及定位提升。可以看出,GPS+BDS双系统相对于GPS单系统定位精度提升了20%~30%,加入Galileo系统,定位精度可进一步提升10%,而加入GLONASS的四系统定位相对于三系统定位仍有5%左右的小幅提升。四系统定位性能最优,水平方向定位精度处于毫米级水平,而高程方向在1 cm左右。 表3 单/双/三/四系统定位平均RMS及多系统定位性能提升 本文基于30 s采样率的数据,采用静态仿动态定位模式,单系统TTFF均在5 min(10个历元)以内,BDS单系统更是在两个历元就实现了模糊度首次固定。组合两个系统,如GPS+GLONASS,实现了首历元模糊度固定。 PPP-RTK是当前最前沿的GNSS精密定位技术。为顺应多频多模发展趋势,PPP-RTK正逐渐由传统的消电离组合模式发展为非差非组合模式。本文针对区域参考网,提出了一种能融合处理CDMA和FDMA两类信号体制的非差非组合PPP-RTK模型。为实现GLONASS FDMA PPP-RTK,利用最新提出的整数可估理论保证了模糊度固定的严密性。利用香港连续运行参考网的GPS/BDS/Galileo/GLONASS数据进行试验,数据采样率为30 s,主要结论如下: (1)在服务端,4个系统的精密改正产品特性一致,组合产品精度均能满足要求。卫星相位偏差在收敛后趋于稳定,Galileo第三频率的卫星伪距偏差在收敛后同样趋于稳定。电离层延迟的估值均在当地14时左右出现最大值,符合电离层延迟的天内变化特性。虽然各产品的精度难以达到相位观测值毫米级的精度,但是组合卫星钟差、卫星相位偏差和电离层延迟的精度与相位观测值的精度一致,因此满足用户精密改正的要求。由于各类产品之间高度相关,对组合产品进行精度评估是有必要的,这更符合实际应用情况,因为用户端是组合各类产品进行改正。 (2)用户仿动态定位试验表明,GPS、BDS和Galileo单系统分别在5、1和3 min内实现了模糊度首次固定,相对于浮点解几十分钟的收敛时间大幅减少。固定解的定位精度相对浮点解显著提升,尤其是在东方向,提升率约为40%。GLONASS单系统模糊度固定依赖于卫星数,当可视卫星数大于5颗时,可在几分钟内成功固定模糊度。组合GPS和GLONASS且只固定GLONASS模糊度实现了快速收敛,证实了GLONASS FDMA整数可估PPP-RTK模型能实现模糊度严密固定同时带来有效定位增益。此外,组合GPS和GLONASS且固定两者的模糊度实现了首历元模糊度固定,相对于GPS单系统,定位精度在东、北、天3个方向上分别提升了9%、12%、14%。组合GPS和BDS同样实现了首历元模糊度固定,相对于GPS单系统在东、北、天3个方向上定位精度分别提升了29%、22%、18%,再加入Galileo观测值定位精度进一步提升了12%、8%、16%,最后加入GLONASS进行四系统定位仍能获得4%、3%、8%的定位增益。 由于本文提出的GLONASS FDMA整数可估PPP-RTK模型假设站间单差IFB可忽略,该模型仅适用于同款接收机的参考网。对于部署多种类型接收机的参考网,可抛弃伪距观测值以避开伪距IFB[23],然后仅基于GLONASS相位观测值,采用本文同样的思路,消除秩亏,并利用整数可估理论构建能实现严密模糊度固定的PPP-RTK模型,这将是未来的研究重点。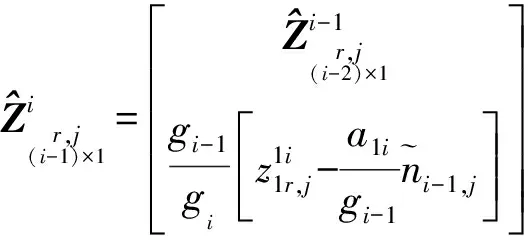
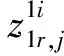
2 试验结果与分析
2.1 试验数据与处理方法
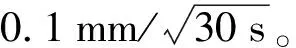
2.2 服务端产品分析
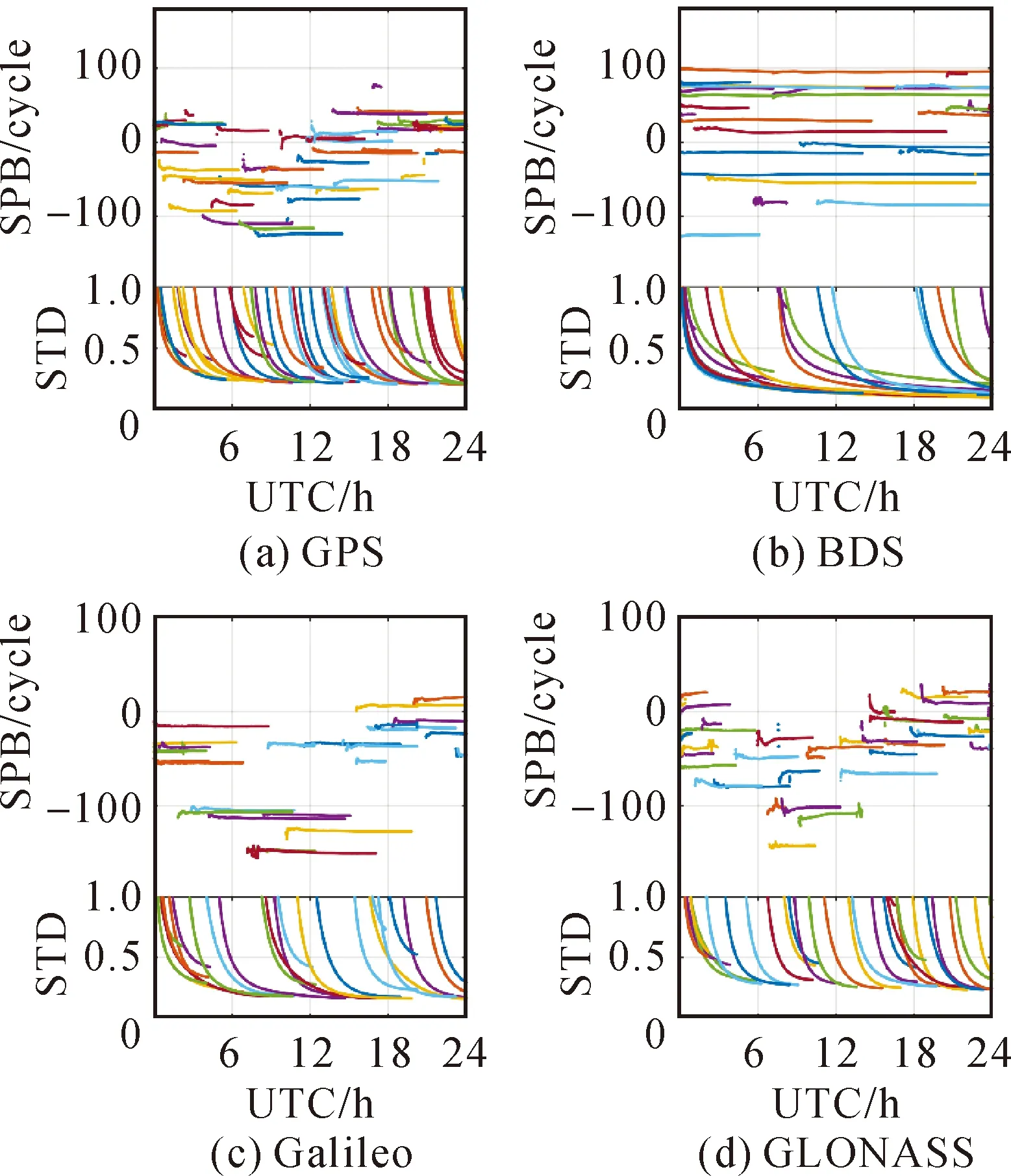
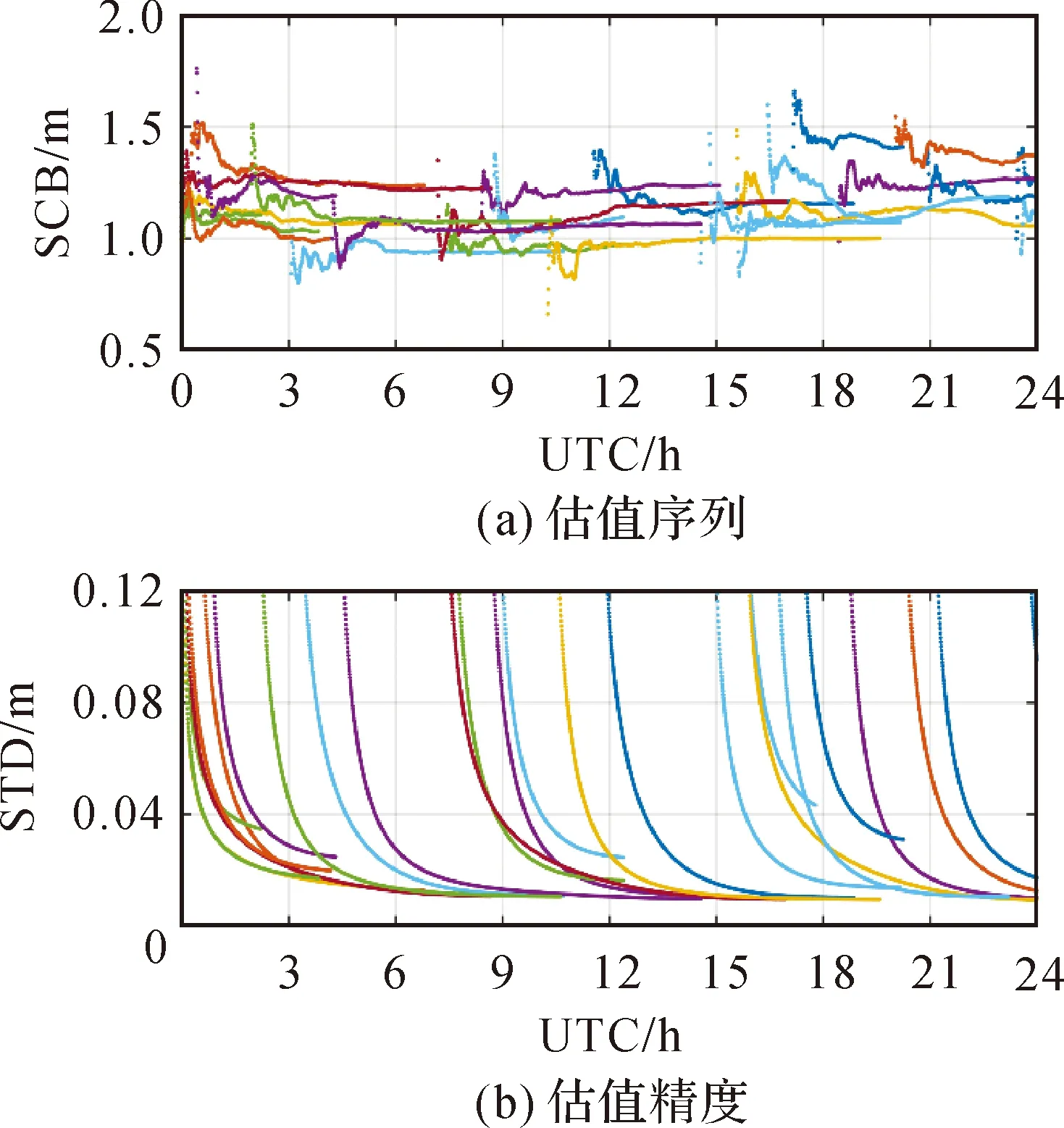

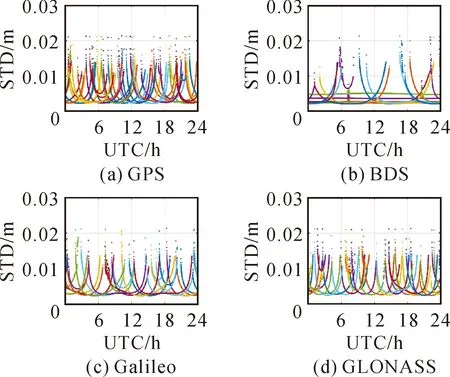
2.3 用户端定位测试
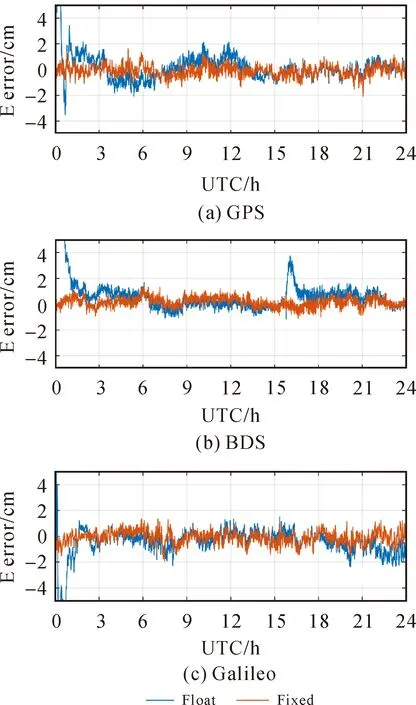


3 总结与展望

