Application of integrated simulation environment SIEMNED to the analysis of the MEPHIST-0 tokamak operation
D Yu SYCHUGOV, S Yu SOLOVIEV, A S ZHILKIN, A V MELNIKOV and S A KRAT
1 Faculty of Computational Mathematics and Cybernetics,Lomonosov Moscow State University, Moscow 119234, Russia
2 National Research Centre, Kurchatov Institute, Moscow 123098, Russia
3 National Research Nuclear University Moscow Engineering Physics Institute, Moscow 115409, Russia
4 National University Moscow Institute of Physics and Technology, Moscow 141701, Russia
Abstract This paper presents the results of numerical simulation of plasma equilibrium and stability in the MEPHIST-0 tokamak with SIEMNED software and comparison of simulation results with experiments.The determined characteristics of the vacuum chamber show that it significantly affects the entire discharge.For various scenarios of the inductor operation, a comparison of experimental data and simulated currents and magnetic fields induced in the chamber was carried out.For steady-state tokamak operation,a numerical study of equilibrium plasma configurations was carried out depending on the currents in the poloidal magnetic field coils and plasma current.The vertical plasma instability was investigated.The limiting values of plasma ellipticity preventing the vertical plasma instability were numerically determined.Numerical simulations show that plasma equilibrium is supported by induced currents.It was shown numerically that magnetic configuration with ‘zero of higher order’ were obtained before the plasma shot,suggesting consistency between the simulation results and observations.
Keywords: mathematical modelling, tokamak installation, MEPHIST-0
1.Introduction
MEPHIST-0 is a small spherical tokamak created at the Department of Plasma Physics of the National Research Nuclear University Moscow Engineering Physics Institute(MEPhI).The research program for MEPHIST-0 involves control of the plasma-wall interactions, including liquid metal technologies,microwave preionization, etc [1].Moreover, since NRNU MEPhI is a scientific and education center, it is planned to use MEPHIST-0 to teach and train students for research on larger tokamaks.This paper presents the results of numerical simulation of processes in the MEPHIST-0 tokamak and their comparison with experiments.
The main determined characteristics of the vacuum chamber allow us to conclude that it has a significant effect over a significant part of the discharge, at least for the planned discharge durations of the installation.It is shown that the characteristic decay time of the induced currents in the chamber is approximately 15-20 ms; therefore, the calculation of the magnetohydrodynamics (MHD) of equilibrium stationary states for this setup will be accurate only for times exceeding this value,and dynamic codes should be used to simulate the initial stage of the discharge, such as DINA [2, 3] or TOKSCEN [4].
A special feature of the magnetic system of the installation is that the coils of the poloidal field (PF) can be seriallyconnected with the inductor or have independent power sources,and different combinations of inductor-connected PF coils can be easily achieved.For various options of switching on the inductor, a comparison of experiments and results of calculations of currents and magnetic fields induced on the chamber was carried out.In the approximation of the stationary mode of operation of the installation, a numerical study of the equilibrium plasma configurations depending on the currents in the PF coils and the current in the plasma was carried out.The vertical instability of the plasma has been studied for variations of equilibrium.Limiting values of the ellipticity E of the plasma cross section have been found at which the plasma instability does not develop.The possibility of generating plasma equilibrium states with a large positive triangularity of the plasma cross section,δsep~ 0.5,and cross section ellipticity, E ~ 1.3, which are stable with respect to vertical displacements,is shown.It is shown that,in principle,it is possible to achieve equilibrium with a large negative cross-sectional triangularity.However all such equilibria are vertically unstable and therefore can only exist with the support of a feedback system, and the current version of the MEPHIST-0 installation does not have one.

Table 1.Basic parameters of MEPHIST-0 [1, 11].
Although the vacuum chamber and the locations of the PF coils of the MEPHIST-0 are vertically symmetrical, calculations have shown that this setup can create equilibrium configurations that are asymmetric in the z-axis and are stable with respect to vertical displacements.
In the calculations, a new software environment SIEMNED was used, which is being developed as a system for integrated modeling of processes in tokamak facilities[5-7].To date, the unified software environment includes numerical codes for calculating the equilibrium,stability,and evolution of plasma in tokamak facilities [4, 8,9];a code for generating three-dimensional grids in regions of complex shape [10]; and a structure and database for developing the information and service.
2.Brief description of the MEPHIST-0 tokamak
2.1.Basic machine parameters
The main design parameters are given in table 1 [1, 11].
Although the MEPHIST-0 installation is small, some of its parameters, primarily the planned value of the toroidal magnetic field, are quite high for installations of this size.Another undeniable advantage of the system is the simplicity of its design, which makes it possible to implement changes to it quickly.This makes it possible to conduct a wide range of experiments using MEPHIST-0.
2.2.Poloidal field coil system (poloidal field coils, central solenoid) of MEPHIST-0
The poloidal magnetic field system of the MEPHIST-0 tokamak consists of four pairs of coils (PF coils) and a central solenoid (CS), located symmetrically relative to the vacuum chamber [21].Their positions are given in table 2 [1, 11].
Amongst the unique features of the magnetic system of this installation, first of all it should be noted that all PF coils are divided into two types.The first type of coils (compensation coils) are serially connected to the CS and therefore have the same current.However,with the help of configuration switching,the direction of current in these coils can be changed to the opposite of the CS current,which will be significant in the future.The CS and compensating coils play the role of the inductor.
The combinations of connecting the CS to the compensation coils are conveniently described by means of special tables [11].As an example, consider the layout configuration shown in table 3[11].Here‘-1’means that one turn from CS is laid into PF1 and PF2 coils and the direction of the current in them is reversed.One turn is also laid into coils PF3, PF4 and PF5,and PF6 from the CS,but the direction of current in them coincides with the direction of current in the CS.Sign 0 means that PF7,PF8 coils are disconnected from the inductor.The CS itself consists of 75 turns.
Coils of the second type have independent power supplies and are designed to control the position and shape of the plasma column.Compensation and control coils have the same coordinates; therefore, when calculating the equilibrium and evolution of plasma for each coil, the main parameter is the total current flowing through it.Such a principle of the magnetic system, which allows the minimization of energy consumption for creation of holding fields, was first proposed in [12].
2.3.Vacuum chamber
The vacuum chamber of the plant has a D-shaped crosssection and is made of steel with a resistivity of 7.2 × 10-7Ω m-1.The thickness of the inner straight part of the wall is 1 mm, and that of the outer part is 3 mm.At the upper and lower toroidal domes,the wall thickness also changes,which is caused by the technology of its manufacture.A general view of the chamber, solenoid, and PF coils is given in figure 1.In our subsequent calculations the vacuum chamber was approximated by a discrete set of 34 filaments, and they are shown in the same figure.
3.SIEMNED software—brief description
SIEMNED (Software and Information Environment for Modeling and Numerical Support of Experiments on complexDevices) is a software and information environment for developing virtual analogues of complex technical devices[5-7].This system is tested primarily on tokamak plants, but in the future, it is planned to expand the range of applicable devices.SIEMNED is based on the Virtual Tokamak software library [5], but its capabilities have been significantly expanded.To date, SIEMNED is a web-based system that includes computational code launchers and automated data exchange tools, as well as a database for storing information about devices, experiments, and calculation results.

Table 2.Positions of coil groups of the poloidal tokamak system MEPHIST-0 [1, 11].

Table 3.Inductor configuration example [11].
SIEMNED consists of a browser client and a server part,which is responsible for performing calculations,storing data,and exchanging between modules.The system on the server is responsible for converting user actions in the browser into commands for computing codes and for data flow between codes, database, and users-reading and writing to the database, and saving computational or user data.The communication between different codes is based on the following idea.For each numerical code, a template of the data necessary for its launch is prescribed in advance.When reading data from a database, the code input data file is generated from this template by pasting data entries from the database into spaces in the template file with corresponding IDs.This approach makes the unified software environment flexible,since to include a new code in the data exchange system is enough to create data template file for this code.
The numerical codes (modules) included in the single environment were created earlier in the last 15-20 years.Currently, the SIEMNED software includes the following numerical codes (modules):
(1) PLASMALESS is a separate module and a modified unit for calculating induced magnetic fields and currents inside the vacuum chamber and on structural elements of the plant.The reason for including this code unified environment is the need to create conditions before the start of discharge to allow the breakdown,which is extremely difficult to do without a detailed calculation of magnetic fields and currents induced in the structural elements of the installation.
The code is based on the numerical solution of the system of Kirchhoff equations for the coils of the PF and the structural elements of the installation [6]:Here L is a matrix of inductances, I is a vector of induced currents on passive elements of the structure,R is a vector of resistances, and Ψ is the total magnetic flux created by magnetic field coils and passive coils.
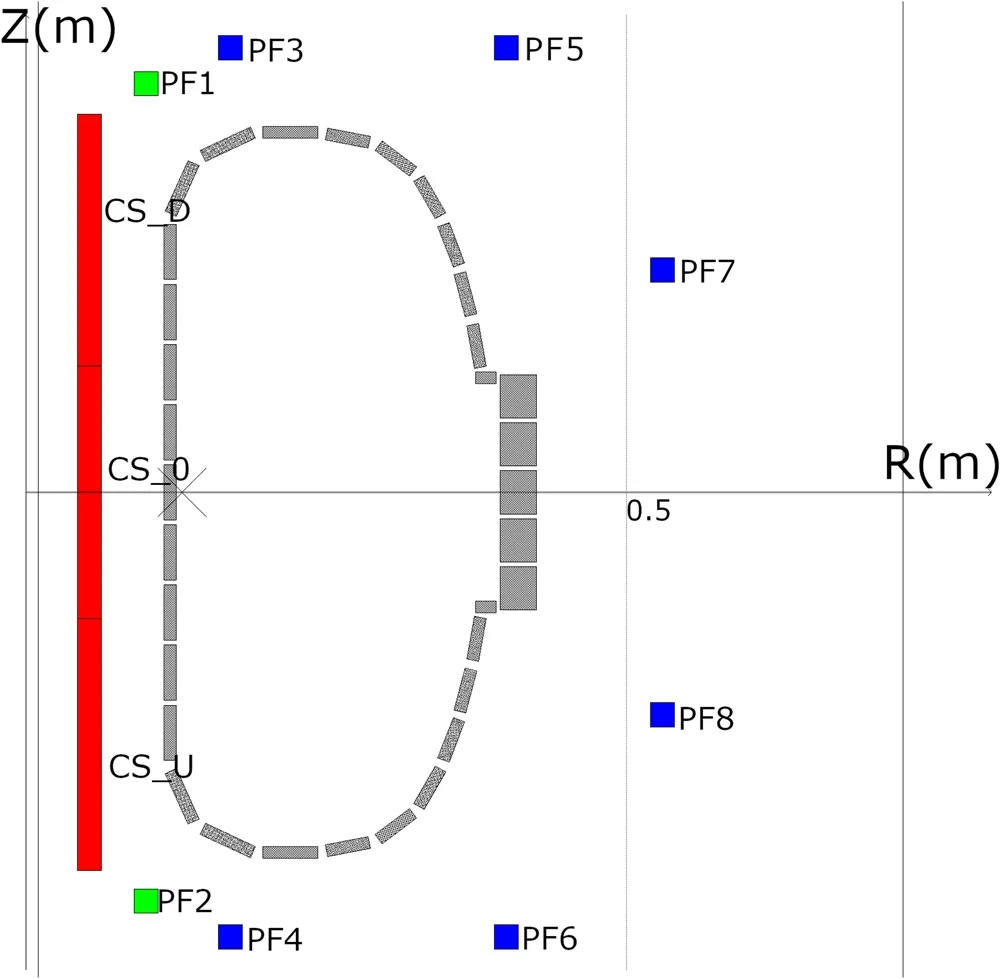
Figure 1.Central solenoid (CS), poloidal field coils (PF), and discrete model of vacuum chamber of the MEPHIST-0 tokamak.
(2) TOKAMEQ is a code for calculating the steady-state plasma MHD equilibrium in a tokamak[8].For the flux of the poloidal magnetic field the problem is solved in an unlimited region,with the conditions of regularity on the main axis of the torus and on infinity
Here,(r,φ,z) is a cylindrical coordinate system with the z-axis directed along the main axis of the torus:γ= 0.8π2is a dimensional factor at which the distance is measured in meters,current in MA,magnetic field in T, and magnetic flux in V·s (Wb);r k,z k,Ikare coordinates of external conductors with current and values of currents (conductors may be considered as infinitely thin or having finite dimensions),respectively;ψpis magnetic flux value at plasma boundary.The plasma boundary itself is initially unknown and is in the process of calculation.
(3) TOKSCEN is a code for calculating the plasma evolution in a tokamak.It is based on the algorithm for the numerical solution of the equations of plasma evolution together with the Kirchhoff equations for conducting elements of the installation design,while at each time step,the quasi-stationary plasma equilibrium is calculated by TOKAMEQ[4].TOKSTAB is a code for calculating the vertical stability of plasma,including the finite conductivity of passive conductive structural elements [9].TOKSTAB exists as a separate code block in TOKSCEN.The code is based on a passive feedback model with both ideal and final conductivity of elements and a‘solid shift’model of a perfectly conductive plasma.Let us assume that the plasma column moves vertically as a solid, and we denote through ξ(t) the offset of the equilibrium plasma position,which is assumed to be small.The setting of the problem consists of the equation of motion for plasma and the Kirchhoff equations for passive coils:
Here M is the mass of the plasma,is the Lorentz force resulting from its displacement,Ikis the induced current in the kth passive coil,FkIkis the returning force from the kth coil,N is the number of coils,Likis the coefficients of their mutual(self-)induction,Riis their ohmic resistance,Lipis the coefficient of mutual induction between the ith turn and the plasma column, and Ipis the full plasma current.Equations(6)and(7)are written in the standard system of units:distance in meters[m],time in seconds[s],mass in kilograms [kg], current in megaamperes [MA], resistance in ohms[Ω],magnetic flux in weber[V·s],magnetic field induction in tesla [T], and self-induction coefficients in microhenry[μH].Details of formulas(6)and(7)are given in [4].Equations (6) and (7) are converted by means of substitutions
As a result, a generalized algebraic problem arises for eigenvalues
where
Then the main eigenvalue of the problem (8), λ0=γ0+ iβ0, satisfying the conditionis calculated.Ifγ0≤ 0,then the plasma is stable.
(4) MESHER is high-performance code for generation of tetrahedral grids based on the specified geometry applicable to areas with complex structure [10].This code is included in SIEMNED as a part of the data transformation block to support numerical 3D problemsolving algorithms.
Although most unstable displacements for configurations with large triangularity and small aspect ratios differ significantly from displacements in the ‘solid shift’ model, the use of such a model,nevertheless,makes it possible to discard obviously unacceptable variants.Further development of the SIEMNED software environment includes the introduction of more advanced numerical codes for calculating the stability of plasma(e.g.SPIDER[13],KINX[14],DCON[15],VALEN[16]) to allow it to tackle a more diverse array of configurations.
4.Vacuum chamber characteristic calculations
4.1.Evaluation of current decay time of the vacuum chamber
One of the most important characteristics of the vacuum chamber is the decay time of induced currents in it.To estimate this time, PLASMALESS code was used.
PLASMALESS code breaks down the structure of the chamber into multiple elements of comparable size.At the beginning of simulation, a uniform current was supplied to the elements of the outer (the thickest, and therefore the best conducting) wall of the chamber and then a system of equation(1)was numerically solved.Figure 2 shows how the currents induced on all the chamber elements depend on time(blue corresponds to outer wall elements; other colors correspond to top, bottom, and inner walls).It is seen that the characteristic time of current decay is 15-20 ms.
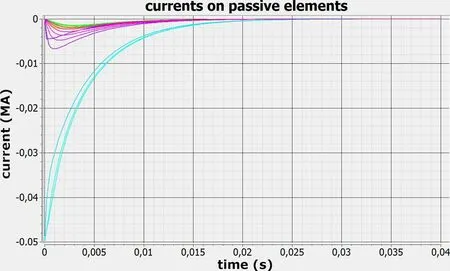
Figure 2.Current decay on the elements of the vacuum chamber.
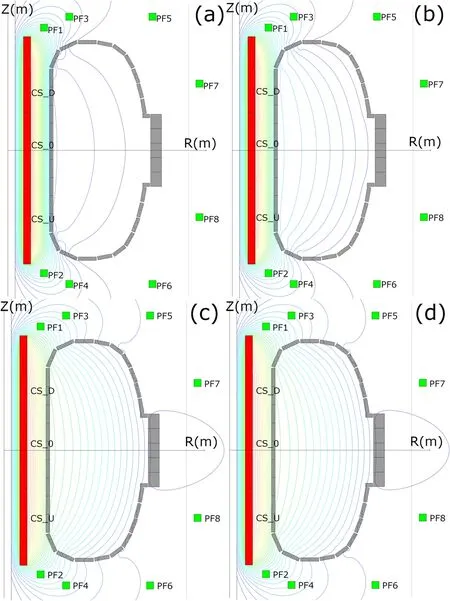
Figure 3.Dynamics of magnetic field penetration into the chamber with only the inductor switched on.Lines of level Ψ=constant for time points of 0.22 ms (a), 0.52 ms (b), 1.52 ms (c), and 2.0 ms (d)are shown in series.
4.2.Calculation of the current induced in the chamber in different inductor scenarios
A specific feature of MEPHIST-0 is the possibility of varied connection of the compensating coils to the CS.The following series of calculations allow one to evaluate what effect can be expected by choosing various connection options.In all calculations,the current in the inductor increased from 0 to 6 kA in 2 ms(that is,taking into account the number of turns,from 0 to 350 kA), but the layout of the inductor was different.The outer part of the vacuum chamber and external toroidal domes have the greatest effect on the confinement of the plasma column, so the most important estimate seems to be total induced current on those parts.
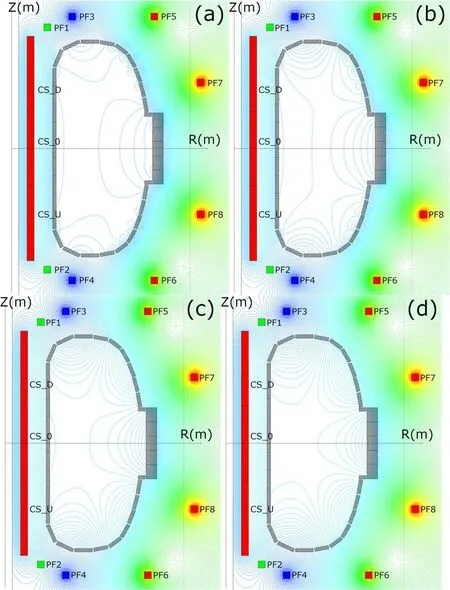
Figure 4.For the second version of the inductor scenario, lines of level Ψ = constant for the same time points are shown in series:0.22 ms(a),0.52 ms(b),1.52 ms(c),2.0 ms(d).Formation of highorder zeros can be seen at 1.52 ms and 2.0 ms.
In the first calculation, the effect of the CS with disconnected compensation coils was investigated.It was found that for 2 ms the total induced current on the outer part of the chamber increased from 0 to-0.5 kA on each of the sections of external toroidal dome from 0 to -1.03 kA.The dynamic pattern of magnetic field penetration in this embodiment is shown in figure 3.The second calculation corresponded to the experiment in the next inductor layout (table 4).
In this case, the picture turned out to be significantly different.Positive currents occurring in coils PF5/6 and PF7/8 led to significant currents of the opposite sign on the outer part of the chamber.For the same 2 ms, the total induced current on the outer part of the chamber increased from 0 to-5.3 kA, and on each of the sections of the external toroidal dome from 0 to about -6 kA.The dynamic pattern of magnetic field penetration according to the second version is shown in figure 4.In this case,at about 1.5 ms near the inner circumference of the chamber, a high-order zero is formed at the magnetic field,which entails the possibility of breakdown and formation of a plasma discharge.Indeed, in the experiment, during the operation of the inductor, in such an arrangement inside the chamber, a discharge similar to an equilibrium one was observed.
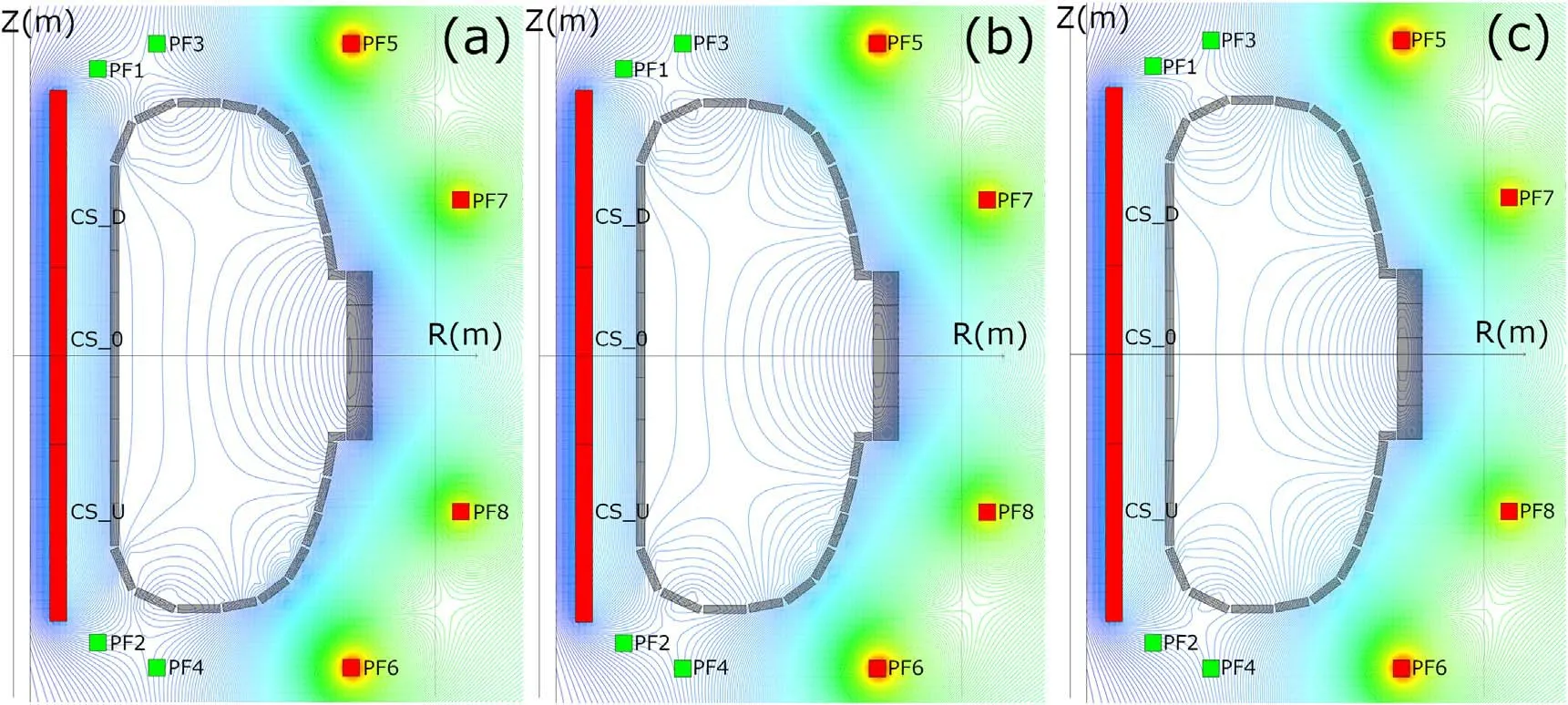
Figure 5.Level lines Ψ = constant at moments t=1.02 ms (a), 1.52 ms (b), and 2.0 ms (c) for the third layout option.
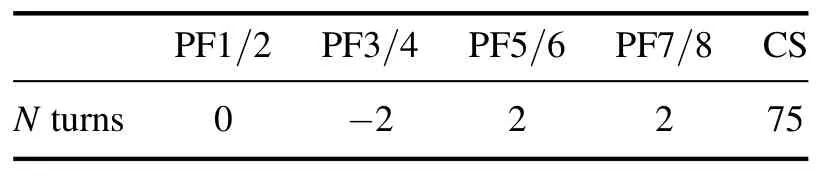
Table 4.Inductor arrangement according to experiments(second version).

Table 5.Arrangement of the inductor corresponding to the second experiment.
The third calculation corresponded to the experiment in the inductor layout variant shown in table 5.Here, the total induced current on the outer part of the chamber at the time of 2 ms was-6.7 kA,and the current on each of the sections of the outer wall rounding was -6 kA.However, unlike the second variant (figure 4), the zero of magnetic field formed here had a lower order, which can, in the case of plasma formation,lead to its ejection up or down,as was observed in the experiment in this case.The corresponding magnetic flux level lines Ψ = constant are shown in figure 5.
Thus, the calculations showed that in order to form an equilibrium at ‘small’ times, it is necessary due to a rapid increase in the currents in PF5/6 and PF7/8 to inject negative currents on the chamber, which will provide equilibrium, but the current in the plasma Iplwill be much less than planned.
4.3.Experimental measurement of the magnetic field inside the vacuum chamber of the MEPHIST-0 tokamak during the inductor pulse
Measurements of spatio-temporal vertical magnetic field distributions in the discharge chamber of the MEPHIST-0 tokamak were made for a number of inductor arrangements.Prototype handmade poloidal coils were used in the experiments.Measurements were carried out using a set of seven magnetic field Hall sensors AH49E with a measurement range from -0.1 to 0.1 T, distributed along the radius of the tokamak near (at a distance of less than 5 mm from) the central plane of the tokamak, similar to the measurements presented in [17].The measurement uncertainty was ~5 Gs.The error margin of sensor verticality was ~5°.The inductor capacitors were charged to an identical voltage of 2 kV in all experiments.The total capacity used was ~11 mF.The measurements were performed while the discharge chamber was vented to atmosphere.No toroidal fields from toroidal coils, or additional PFs from poloidal coils unconnected with the inductor,were applied.A ring limiter and an RF antenna were installed in the discharge chamber during measurements.Figure 6 shows the measurement results for an inductor arrangement consisting only of a CS(figure 6(a))and a comparison similar to that shown in table 4 (figure 6(b)).
For the experiment with the CS only, one can see that magnetic field temporal distribution follows current temporal distribution with only a slight delay ~0.1 ms, and the discharge chamber works as an analogue integrator for the magnetic field signal.Radial distribution of the magnetic field agrees with the predictions of the model(figure 3);that is,the field strength decreases with major radius, as expected.
In the case of(0-2 2 2)inductor configuration,the spatiotemporal distribution of the vertical magnetic field was qualitatively different.For the first ~0.5 ms, the vertical magnetic field was ~0 in all measured points.After that time, the vertical magnetic field started to increase.It is interesting to note that the magnetic field increased first at the outer radius, and at a given time,the magnetic field was smaller at a smaller radius and higher at a higher radius.This could be due to the large RF antenna installed near the outer wall of the vacuum chamber,which could introduce fluctuations into local inducted currents.The largest increase in magnetic field started only after ~1.4 ms, when the slope of current pulse in the inductor circuit changed signs.
Based on the obtained experimental data,one can observe qualitative agreement with the model predictions.Deviations between the model and experimental data can be explained by the presence of large inter-chamber elements, as well as the imperfect forms of the PF coils, which were handmade for the experiments.
5.Calculation of magnetohydrodynamics of plasma equilibriа
As described above, the discharge initiation and formation in the MEPHIST-0 tokamak is greatly influenced by the vacuum chamber.Since the discharge duration is expected to be about 30 ms or even longer, full MHD equilibrium calculations are of importance.
5.1.Comparison of DINA and TOKAMEQ calculations
Although the results of the calculations on the DINA [2, 3]and TOKAMEQ codes were repeatedly compared and showed good agreement [18, 19, 22], we still started by making such a comparison again.For comparison, the magnetic system variant calculated earlier in [11] was taken and described in tables 6 and 7.
Thus, taking into account directions of currents in turns and their number, the total values of currents in the inductor and in the coils of the PF for the ‘test’ configuration [11] are taken as in table 8.
The equilibrium plasma configurations for MEPHIST-0 installation calculated by means of the DINA and TOKAMEQ codes at a total current in plasma of 160 kA,and at the sizes of external currents given in table 8, are shown in figures 7(a) and (b).There is a good agreement between the calculation results.Since more detailed comparisons of the results of the calculations on the two codes were made earlier,one such test is sufficient.In the future, this equilibrium configuration will be called ‘basic’.
The agreement of the results of calculating the ‘basic’equilibrium according to two different independent codes DINA and TOKSCEN allows us to conclude that at the time of MEPHIST-0 installation it is possible to achieve the planned parameters, but at times of more than 20 ms (the time of complete decay of currents in the chamber), the presence of a sufficiently powerful power supply of the installation is required.
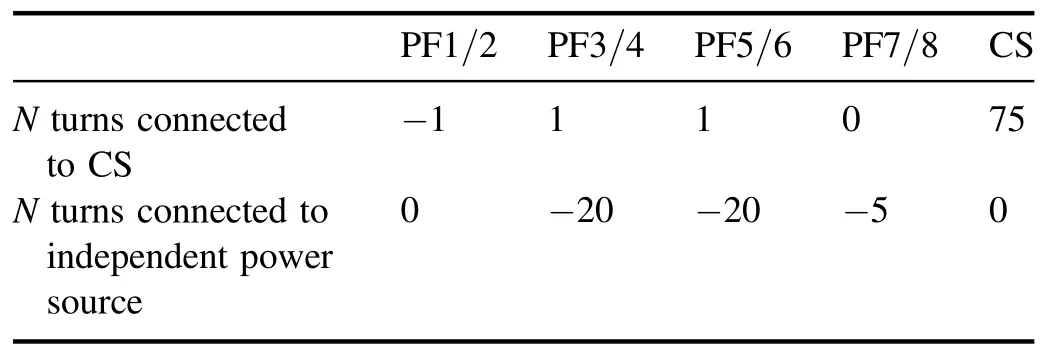
Table 6.Inductor and poloidal coil arrangement for configuration calculated in [11].
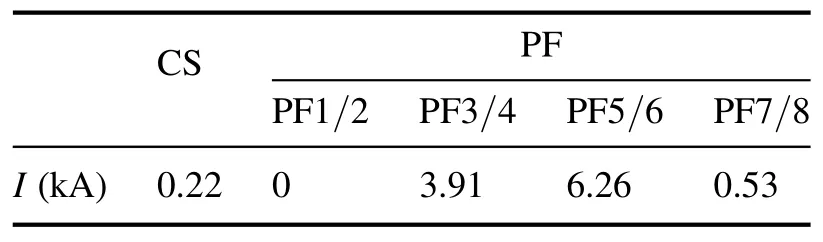
Table 7.Values of currents in one turn of the poloidal system specified in table 6 [11].

Figure 7.Comparison of equilibrium MHD calculations for MEPHIST-0 performed by codes DINA (a) and TOKAMEQ (b).

Table 8.Total currents in the inductor and coils of the PF,taking into account the number of turns.
5.2.Study of dependence of plasma radius on plasma current
During calculations, the arrangement of the inductor and the values of external currents corresponded to the ‘basic’ version.The plasma boundary in all calculations passed through a limiter with coordinates r=13 cm, z=0 cm (indicated in figure 7(b) by a cross).
Calculations showed that at ‘basic’ sizes of currents in the operating coils the smallest size of current in plasma at which there can be a balance is about 100 kA,and the greatest at which the plasma column is still located in the chamber is about 190 kA.The dependence of the radius of the plasma column on the plasma current is shown in table 9, and the obtained equilibrium configurations are shown in figure 8.
5.3.Elongated plasma configurations
Due to the fact that most modern tokamak installations have an elongated cross section of the plasma column, the possibility of obtaining such configurations on MEPHIST-0 is of great interest.However, such configurations tend to be vertically unstable.Since currently there are no active feedbacks on MEPHIST-0, only those equilibria that are stable in themselves can be actually obtained without taking into account the influence of the vacuum chamber.

Table 9.Plasma radius versus plasma current.
To find such configurations we used the ‘basic’ version as the starting point.In further equilibrium calculations,currents in PF3 and PF4 were increased while other coils currents remained the same.Calculations show that with a plasma current of Ipl=160 kA and values of total current in PF3/4 equal to 50 kA, the plasma column grew too big for the chamber(figure 9(a)).Plasma current of Ipl=110 kA required that currents in PF3/4 were approximately 160 kA for the plasma to remain vertically stable.In this scenario, plasma elongation E equals 1.21, triangularity of separatrix δsep=0.145 and triangularity of 95% flux surface δ95=0.11 (figure 9(b)).More interesting was the version of Ipl=130 kA (figure 9(b)).This case showed ellipticity E=1.26, and the plasma remained vertically stable within the rigid vertical shift model.This effect can be explained by the large triangularity of the column section,which is δsep=0.3 at the separatrix, and on 95% flux surface δ95=0.26.The values of currents in the coils for this configuration are given in the first row of table 10.

Figure 8.Equilibrium states corresponding to the plasma current: (a) 100 kA, (b) 130 kA, (c) 190 kA (all stable).

Figure 9.Ellipticity limit stable equilibrium at current in plasma:(a)160 kA,(b)110 kA,(c)130 kA(values of poloidal currents are given in the first row of table 10).
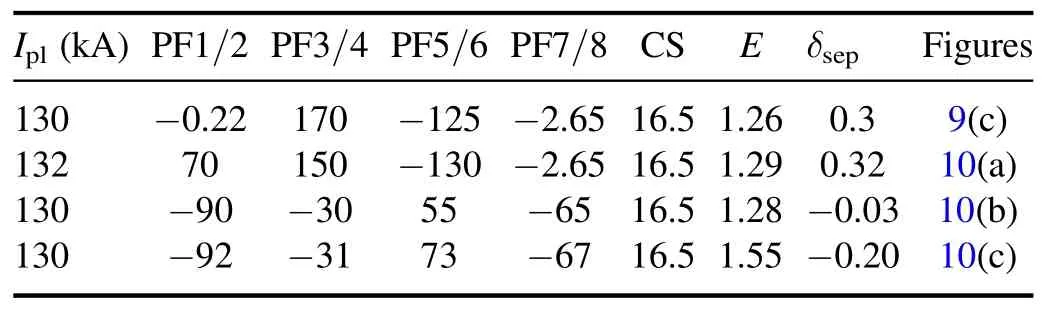
Table 10.Control of plasma triangularity.
5.4.Control of plasma triangularity
Higher values of plasma cross section triangularity typically correlate with improved vertical stability.However, the advantages of positive triangularity have not been absolutely established and need further verification.Experiments on TCV and DIII-D showed that negative triangularity contributes to improved plasma confinement[18].Although configurations with negative triangularity were not initially planned on the T-15 MD, it turned out that there is such an opportunity [19].It would be interesting to know what possibilities the installation of MEPHIST-0 has in that regard.
The most promising ‘starting point’ for increasing the triangularity was the configuration shown in figure 9(c)); the values of external currents are given in the first line of table 10.Since PF5/6 coils are far from the plasma column,their effect on triangularity was small.Coils PF1/2 have a more significant but also limited effect, and an increase in current in them should be accompanied by a decrease in current in PF3/4.As a result, an ‘improved’ configuration was found, with parameters E=1.29 and δsep=0.32, also stable with respect to vertical shift.The values of currents in the coils for the ‘improved’ configuration are given in the second row of table 10, and the level lines Ψ = constant are shown in figure 10(a).
A different pattern occurs when the triangularity of the section decreases.All found configurations, even with small negative δsepvalues, have proven to be unstable vertically,and therefore they can only be implemented if the installation of MEPHIST-0 has a feedback system.An example of such unstable equilibrium is the structure with E=1.28 and δsep=-0.03 (the third row in table 10, figure 10(b)), where the increment of instability development is 137 s-1.However,the existing coil system can, if stabilized, create equilibrium with sufficiently large negative δsepvalues.One of these configurations (the fourth row of table 10, figure 10(c)) has plasma column characteristics E=1.55 and δsep=-0.20.At the same time,the increment of instability development is about 400 s-1for this equilibrium, and without additional stabilizing coils and an active feedback system, it cannot be created.

Figure 10.(a) ‘Improved’ configuration with δsep=0.32, E=1.29 (stable), (b) low negative configuration triangularity δsep=-0.03,E=1.28 (unstable), (c) with parameters E=1.55 and δsep=-0.20 (unstable).
It was found that the ability to control the triangularity of the plasma section on MEPHIST-0 with the current geometry of the magnetic coils is limited,primarily due to the positions of PF5/6, which are located too far from the vacuum chamber.The maximum positive triangularity value achieved in this case is δsep=0.32.The second reason is the vertical instability of plasma already developing at low negative values of δsep, which requires a feedback system to suppress,which is currently absent.
5.5.Study of the possibility of creating vertically(z)asymmetric equilibrium
Almost all, both existing and modern, tokamak installations under construction have an asymmetric z-section of the plasma column, so the task of creating and controlling such configurations on MEPHIST-0 is paramount.PF3/4 coils have been found to be quite suitable for holding such asymmetric equilibrium (here we are talking about equilibrium,and not about the necessary feedback in this case).Since the‘improved’ configuration, when shifted up and down, will inevitably touch the outer section of the chamber wall(figure 9(a)),we chose a z-symmetric configuration,similar to the ‘improved’ version, but with a slightly lower plasma current value, Ipl=120 kA.Further, the position of the magnetic axis along z was shifted upward,and the imbalance of forces acting on the plasma column was compensated by an increase in the current in the coil PF4, with an unchanged current value in PF3.It was found that the plasma column,moving the equilibrium in the upward direction, retains its stability up to the displacement value along the z-axis byΔz=3.2 cm, while the value of current change in PF4 is required to be small, of the order of 1 kA.The equilibrium level lines Ψ = constant are shown in figure 11.
Table 11.Configurations with large triangularity.
5.6.On the possible modifications of the tokamak magnetic system
The most realistic of the possible modifications of the magnetic system of MEPHIST-0 is the change in position of one of the control coils of the magnetic field.We made a calculation for a case if PF5/6 were moved closer to the chamber, with new coordinates r=34 cm, z=±29 cm.It was found that in this case it was possible to obtain a vertically stable (excluding the chamber) ‘divertor’ configuration,while δsep=0.48, E=1.29.The values of currents forming this equilibrium are given in the first line of table 11,and lines Ψ = constant are given in figure 12(a).Given the ‘ductility’of the installation to the alterations, such movement of the coils PF5/6 does not seem unthinkable,and the only question that remains is whether the required current values can be maintained in the control coils.
To conduct experiments with a large negative triangularity,the design of the installation requires more serious alterations.Although an adjusted coil arrangement can provide an equilibrium with a large negative triangularity and a large ellipticity of the section, δsep=-0.34, E=1.48 (second line of table 11,figure 12(b)), at the same time, the plasma becomes vertically unstable with a very large incrementγ0~ 750 s-1,which makes it impossible to maintain such an equilibrium with only active feedbacks.

Figure 11.Vertically stable configurations with high triangularity: (a)double-null vertically symmetric,(b)single-null upward displaced by 2 cm, (c) single-null upward displaced by 3.2 cm.
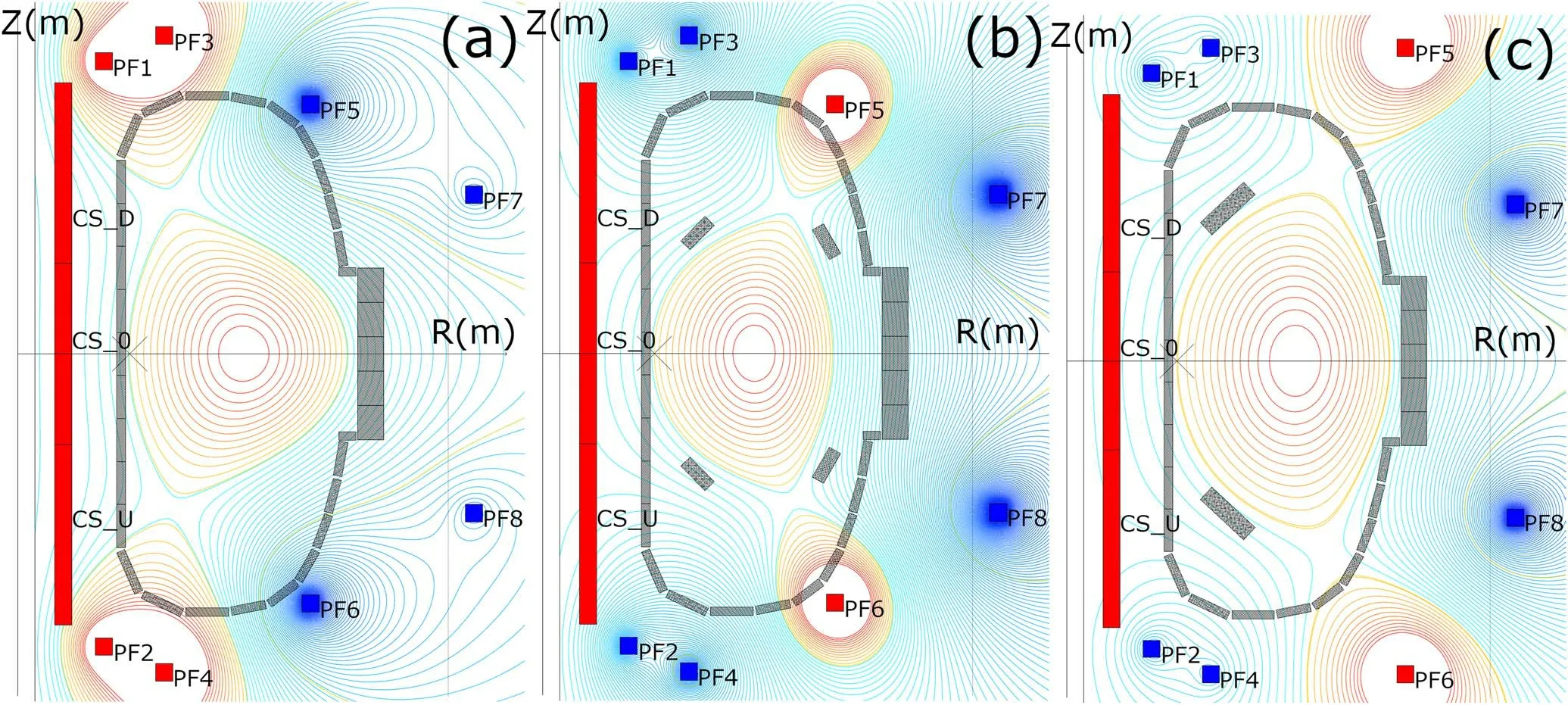
Figure 12.Equilibrium configurations for plant design changes.(a) δsep=0.48, E=1.29 (position changed PF5/6, stable), (b)δsep=-0.34, E=1.48 (changed position PF5/6, additional coils are required for stabilization), (c) δsep=-0.20, E=1.55 (the mutual arrangement of the plasma and stabilizing coils for configuration is shown in figure 10(c)).
Although redesigning the MEPHIST-0 chamber at the very beginning of the experiments seems unlikely, numerical modelling can point to what additional capabilities such redesign would provide for the installation.We considered two versions of the passive turn system.Within the framework of the modified geometry of the coils for stabilizing vertical instability,a system of stabilizing coils similar to the T-15 MD was considered: two pairs of coils made of CuCrZn alloy,closed in pairs according to the top-bottom system,4 cm long and 2 cm thick,and located as indicated in figure 12(b).At the same time, the amount of instability increment decreases after introducing coils from 750 to 16.7 s-1,which is quite acceptable for an active feedback system.
If you remain within the existing geometry of the coils,then for equilibrium, the rate of development of vertical instability of the plasma for equilibrium shown in figure 10(c)can be reduced to acceptable valuesγ0~ 20 s-1using only one pair of passive coils, 7 cm by 2 cm, closed to each other.Using these,it is possible to reduce the growth rate from 400 to 20 s-1.The mutual arrangement of the plasma and stabilizing coils for this configuration is shown in figure 12(c).
6.Conclusions
During the decay time of the toroidal current passing through the vacuum chamber (~1 ms), plasma equilibrium is ensured by these induced currents.
Designed parameters of discharge (plasma current Ipl= 160 kA, triangularity δ=0.4) are achievable for longer discharge duration with independent power sources for control PF coils.
MEPHIST-0 is a flexible tokamak,allowing a wide set of vertically stable steady-state magnetic configurations with positive triangularity, and also negative triangularity after introducing additional stabilizing (passive control) coils inside the vacuum chamber.This flexibility significantly extends its capabilities from solving purely educational problems to the studies of high interest: coupling of the plasma confinement to the features of the configuration.
The steady-state equilibrium configurations obtained in the SIEMNED software were verified by DINA code for equilibrium evolution.It was shown numerically that magnetic configuration with ‘zero of higher order’ was obtained before the plasma shot, suggesting consistency between the modelling and observation.Further development of the SIEMNED system includes introduction of other codes,foremost of which are more broadly applicable codes for plasma stability calculations [13-16, 20].
Acknowledgments
The mathematical part of the paper was done with the financial support of the Ministry of Education and Science of the Russian Federation as part of the program of the Mathematical Center for Fundamental and Applied Mathematics(No.075-15-2019-162)and partly RFBR(No.20-07-00391).
 Plasma Science and Technology2023年3期
Plasma Science and Technology2023年3期
- Plasma Science and Technology的其它文章
- Improvement of a temperature response function for divertor heat flux monitoring in fusion devices
- Degradation of sulfamethoxazole in water by dielectric barrier discharge plasma jet:influencing parameters, degradation pathway, toxicity evaluation
- Experimental investigation of dynamic stall flow control using a microsecond-pulsed plasma actuator
- Laser-assisted ablation and plasma formation of titanium explored by LIBS,QCM, optical microscopy and SEM analyses along with mechanical modifications under different pressures of Ar and Ne
- Study on the effect of focal position change on the expansion velocity and propagation mechanism of plasma generated by millisecond pulsed laser-induced fused silica
- Degradation of antibiotic contaminants from water by gas-liquid underwater discharge plasma
