基于贝叶斯推理的包装件动力学模型优化选择研究

朱大鹏，余珍，曹兴潇

装备防护

基于贝叶斯推理的包装件动力学模型优化选择研究

朱大鹏a，余珍a，曹兴潇b

（兰州交通大学 a.交通运输学院 b.机电工程学院，兰州 730070）

在多种类型的模型中挑选出最优包装件模型，并实现参数识别的方法。文中将包装件模型构建为参数不确定模型，在贝叶斯推理的框架下，采用马尔可夫链蒙特卡洛法识别模型参数，采用偏差信息准则（DIC）计算各备选模型的DIC参数，选择出最优包装件模型。在振动实验台用质量块–缓冲材料模拟包装件并进行随机振动测试，分析结果表明，Bouc–Wen（=2）模型为文中包装系统的最佳模型。文中提出的基于贝叶斯推理的包装件模型优化选择和参数识别方法考虑了模型不确定性，构建的模型可准确预测包装件在随机振动下加速度响应的时域信号。

模型选择；贝叶斯推断；马尔可夫链蒙特卡洛；Metropolis–Hastings算法；偏差信息准则

包装件在流通过程中，由于长时间受到振动载荷的作用，包装件中的产品在振动载荷作用下可能产生损坏。为降低产品损坏概率，需构建包装件模型，分析包装件在振动载荷下的响应，找出影响包装件响应的因素，提出优化包装设计的方案。构建准确的包装件模型，是准确分析包装件响应、判断包装件可靠性和安全性的重要基础。

在振动载荷下，如何准确构建结构模型并进行模型参数识别，在结构响应预测、结构状态监控、故障诊断等领域，是一个关键问题，近年来该问题受到了国内外研究者的广泛关注。De等[1]考虑了结构非线性和参数不确定，将结构响应划分为两部分：系统的名义线性部分和系统修正部分，其中修正部分的响应用神经网络建模。Scheel等[2]提出了在谐波激励和随机激励下非线性系统识别方法，该模型可准确模拟非线性系统在共振状态的响应。Esfahani等[3]提出了一种识别Bouc–Wen模型的黑箱模型，采用多项式解耦对模型进行了简化。Chen等[4]和Jin等[5]构建实验系统，结合传统线性系统测试数据和基于高速摄像系统的图像处理结果，提出了非线性结构识别方法。Civera等[6-7]将电路识别领域中的向量拟合法进行改进，提出用于结构特性识别的快速松弛向量拟合法，该方法已成功用于工程结构识别和建模中。朱大鹏等[8-9]将包装系统简化为单自由度振动系统，提出了随机振动载荷和冲击载荷条件下系统参数识别方法。由于可以采用多种模型描述一个给定的振动系统，在这些模型中，需要优化选择一种最佳模型，减小模型响应误差。Fuentes等[10]在单自由度系统中构建各种可能的非线性弹性和阻尼函数库，在稀疏约束条件下，采用标准Lasso回归选择单自由度模型中最优的弹性和阻尼函数类型。Safari等[11]系统对比了目前常用的非线性系统识别方法，实例分析表明，混合式方法可准确识别出复杂的系统弹性和阻尼特性。

文中将包装件模型简化为单自由度系统，考虑到模型的不准确性、实验数据受噪声污染等因素，将模型构建为参数不确定的模型，应用贝叶斯推断法推断识别模型的不确定参数。包装件模型可用多种模型类型表征，文中采用DIC准则（Deviance Information Criterion）对这些模型进行对比，比选出最优包装件模型。

1 包装件模型的不确定性

将包装件简化为单自由度支座激励系统，对该系统进行实验测试，记录输入和输出数据，并识别包装件模型参数。由于以下原因，包装件模型中存在着不确定性。

1）包装件模型存在着误差。虽然目前可采用各种线性和非线性模型对包装件中的弹性特性和阻尼特性建模，但大部分的缓冲材料在载荷作用下变形和能耗机理尚不清晰，其本构模型尚未完全建立，故目前采用的模型与真实的缓冲材料特性之间存在着误差。

2）实验过程中噪声污染。在实验数据记录过程中不可避免会受到噪声影响，这也会影响模型参数识别。

3）记录的数据有限。实验过程中只能记录有限长度的数据，用这些数据表征包装件特性时也会造成一定的误差。

考虑到上述模型中存在的不确定性，文中将包装件模型看作是具有不确定参数的振动模型，根据实验数据识别出的模型参数不是确定的值，而是具有一定分布的不确定参数：

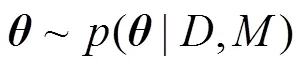
式中：为包装件模型中的参数向量，对于线性弹性–阻尼模型，=[,]，对于Bouc–Wen模型，=[,,,]；为采集的实验数据；为选择的包装件模型。由于包装件模型的不确定性，应用该模型预测包装件响应时，也具有不确定性：

式中：为包装件受到的激励。的分布可由式（3）确定。

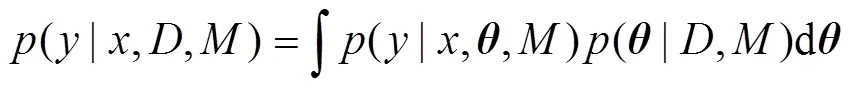
2 包装件模型的识别

对于不确定的包装件模型，可采用Bayesian推断法确定其模型参数：

式中：(|)称为模型的似然函数；()为模型参数的先验分布，分母()由式（5）确定。

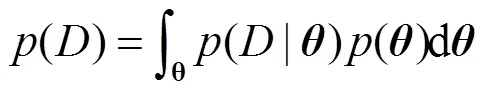
式中，分母()是一个归一化函数，确保式（4）获得的函数是一个概率密度函数，故式（4）可简化为式（6）。

可用式（6）估计包装件模型参数分布，再进行归一化处理。先验分布函数()通常根据经验确定。对于似然函数，假定模型预测的包装件响应(t,)和真实记录的包装件响应y之间的误差为ε，即：

其中，为采样点个数。假定式（7）中各采样点误差互相独立且呈正态分布，则似然函数由式（8）确定。

其中，为模型响应和真实响应误差过程的标准差。直接根据式（6）求出包装件模型参数是很困难的，在Bayesian推断框架下，可采用马尔可夫链蒙特卡洛（Markov Chain Monte Carlo, MCMC）法[12]识别参数，该方法的基本原理是对参数构建一个平稳分布的马尔可夫链，通过合理控制的变化，该马尔可夫链的分布最终收敛于(|)，即应用马尔可夫链生成一系列参数[0,1,2,…]，随着生成的参数数量的增加，可确保参数符合(|)分布。文中采用Metropolis–Hastings算法[13]设置参数马尔可夫链，具体步骤如下：

1）设置马尔可夫链总长度，令=1，估计初始参数值0，令(t)=0。

2）令=+1，根据状态转移函数(*|)生成*。

3）根据式（8）构建的似然函数计算：

4）如果≥1，则接受*为新的参数，否则以概率接受*为新的参数；

5）如果*被接受为新的参数，则(t+1)=*，否则(t+1)=。

6）重复步骤2—5，直至=。

通过合理选择和状态转移函数中的参数，参数马尔可夫链可较快收敛至真实参数范围，可用收敛后的马尔可夫链近似估计真实的系统参数。

3 识别最优模型

对于一个给定的包装系统，可采用多种类型的模型分析该系统特性，在每个模型类型框架下，根据实验数据，可识别出每种模型的参数。如，对于单自由度包装件模型，可采用线性振动系统、非线性弹性振动系统、非线性阻尼振动系统、Bouc–Wen系统等对包装件进行参数识别和响应预测，因此，需要对比各类模型，优选出最佳模型，用于对包装件进行响应预测。

为优选模型，定义模型偏差参数()[14]：

()=−2log(|)+(10)

式中：为常数。似然函数(|)由式（8）确定，很显然，模型偏差参数()越小，模型准确性越好，在对各模型进行对比时，常数可不予考虑。由于对模型参数识别时，为随机变量，故()也具有随机性，()的均值可通过蒙特卡洛法确定：

式中：为采样个数；为采样的参数值；[ ]为求期望值运算。定义模型参数有效数：

4 实例分析

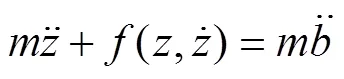
对于线性振动模型，包装系统运动方程式为：

式中：m，c和k分别为质量、阻尼系数和弹性系数，由于实际中m值很容易获得，故线性振动模型中，需识别的参数为θ=[k,c]。

对于Bouc–Wen模型[17]，包装系统运动方程为：

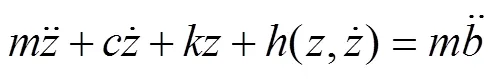
其中，

在式（16）和式（17）中，参数和均代表材料弹性参数，在式（16）中可将和统一考虑，故在Bouc–Wen模型中需识别的参数为=[,,,]。

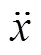
1）根据线性振动模型和Bouc–Wen模型基本特性，预估模型初始参数0。

2）根据0采用龙格库塔法模拟系统加速度响应(t,0)。

3）计算模拟响应和真实响应之间的误差，根据式（8）计算似然函数。

4）在Metropolis–Hastings算法中重复步骤2和3，迭代分析求出参数的马尔可夫链数据。

在以上算法步骤中，需注意以下事项：

1）在Metropolis–Hastings算法中，状态转移方程采用高斯函数，即马尔可夫过程的下一个状态根据一个高斯函数确定，其均值为当前状态，即：(*|)～(,)，其中( )表示正态分布。文中确定各具体参数下一状态时，需合理选择正态分布中的值，该值选择过大或过小都会造成马尔可夫过程收敛速度慢的问题。

2）参数初始值0应合理选择，以提高参数马尔可夫过程的收敛速度。

3）在计算能力允许的前提下，尽可能增加Metropolis–Hastings算法的迭代次数，即使参数初始值0的选择和状态转移方程中的选择存在误差，随着的增加，也可收敛至真实参数值。

根据以上算法步骤，设定迭代运算10 000次，分别识别线性振动模型和Bouc–Wen模型（=1,2,3,4）参数的马尔可夫过程，去除燃烧期（为准确起见，文中选择前4 000个数据作为燃烧期），各模型参数分布情况如表1所示。从表1结果可以看出，考虑到模型的不确定性，可将包装件用参数不确定的模型表示，相应地，在给定振动载荷下，包装件的响应也是不确定的值，是在一定范围内波动的。对于一个给定的包装件，由于存在多个可描述其振动特性的模型，文中采用DIC准则优选出最佳模型，根据识别出的模型参数计算各模型响应，对比包装件真实响应分析各模型的响应误差，采用式（11）—（13）计算各模型的DIC值，如表1所示。从表1中可以看出，Bouc–Wen模型（=2）的DIC值最小，用该模型是这些模型中的最佳包装件模型。文中识别出的Bouc–Wen模型（=2）参数分布如图2所示。根据图2的参数识别结果，可将各识别的参数结果近似看作正态分布，识别出各参数的均值和方差，如表1所示，这些参数识别结果可作为模型响应预测的依据。

在得到包装件的最优模型及模型参数后，可用式（3）预测该不确定模型的响应，首先对包装件模型中的不确定参数离散化，将式（3）的积分处理为不确定离散参数下的模拟，模拟的包装件响应和实验记录的真实响应如图3所示，实线为实验记录的质量块的加速度响应，虚线为对Bouc–Wen模型（=2）参数离散化处理后预测的包装件响应的包络线。从图3可以看出，利用该模型预测的包装件响应是一个不确定的振动响应，该模型可准确预测包装件的响应，且考虑了包装件模型中的一些不确定性。根据识别出的模型类型及参数，可对包装件在运输中的安全性和可靠性进行评价分析。

表1 各模型参数及DIC值

Tab.1 Parameters and DIC values of each model

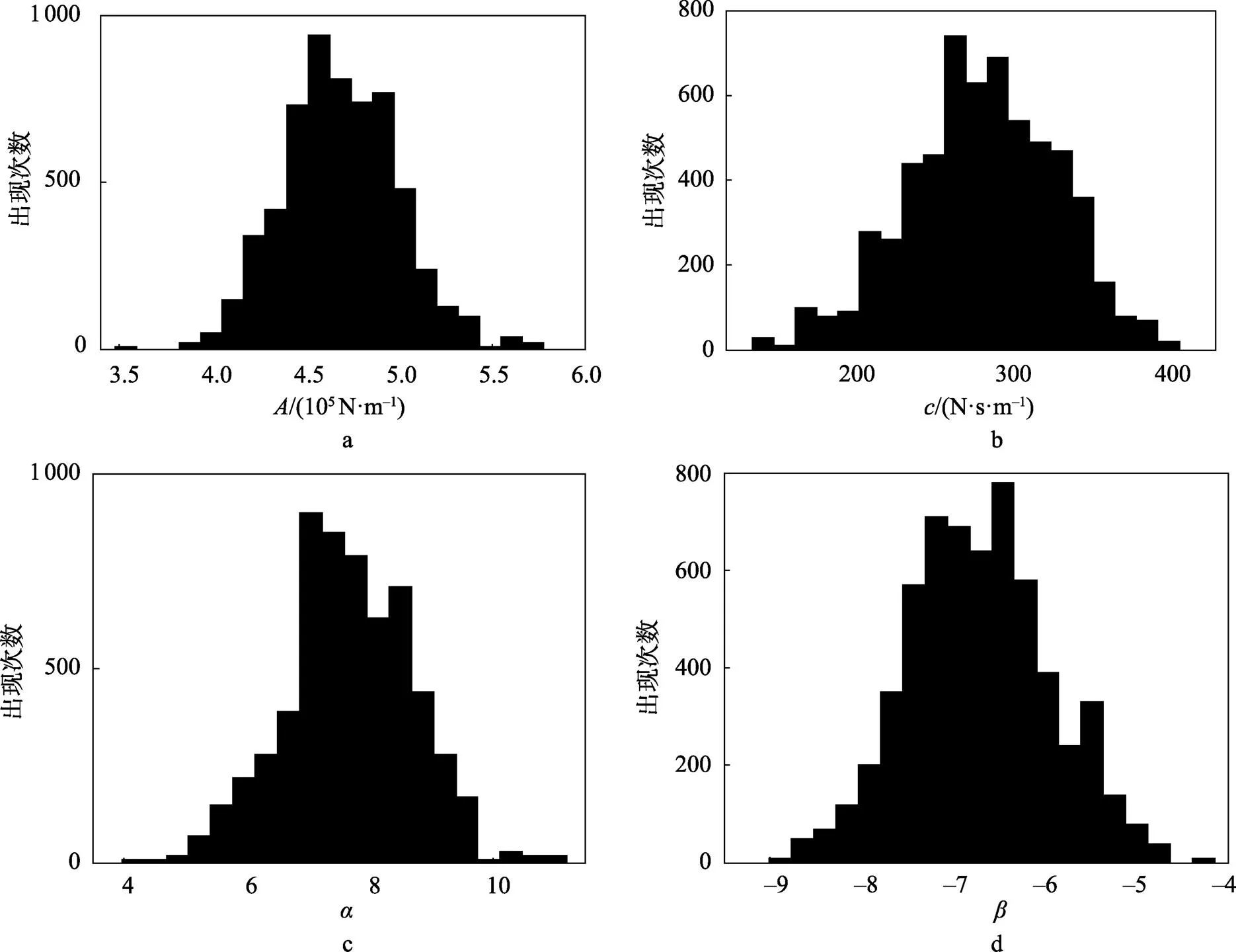
图2 Bouc–Wen模型（n=2）参数分布

图3 模型预测的包装件响应和真实响应对比

4 结语

文中考虑了包装件模型中的不确定性，在贝叶斯推断框架下构建包装件模型，采用马尔可夫链蒙特卡洛法识别各备选模型参数，采用偏差信息准则优选出包装件最优模型。文中得出主要结论如下：

1）考虑到模型的不确定性，在贝叶斯推断框架下，没有一个模型能够精确无误地描述包装件动态特性，只能在一系列备选模型中选择出最近似的模型。在文中的包装系统中，Bouc–Wen模型能够更好地描述包装件的振动特性，该模型考虑了模型中的不确定因素，能够准确预测包装件的响应。

2）文中提出的基于Metropolis–Hastings算法的马尔可夫链蒙特卡洛参数识别方法需对参数初始值和状态转移函数中各参数的方差合理选择，以提高参数收敛速度，减小计算量。

3）偏差信息准则综合考虑了模型的准确性和复杂性，是优选最优模型的有效方法，该算法具有计算效率高、普适性好的特点，该方法不仅适用于包装模型的选择，在结构、电气、机械等领域也可广泛应用。

4）在备选模型中只选用了线性模型和Bouc–Wen模型，在今后研究中，可根据包装件响应的时域和频域特性，在备选模型中增加其他类型的模型进行优选，以提高模型选择的准确性。

[1] DE S. Uncertainty Quantification of Locally Nonlinear Dynamical Systems Using Neural Networks[J]. Journal of Computing in Civil Engineering, 2021, 35(4): 04021009.

[2] SCHEEL M, KLEYMAN G, TATAR A, et al. Experimental Assessment of Polynomial Nonlinear State-Space and Nonlinear-Mode Models for Near-Resonant Vibrations[EB/OL]. 2020: arXiv: 2011.08520. https://arxiv. org/abs/2011.08520

[3] ESFAHANI A F, DREESEN P, TIELS K, et al. Parameter Reduction in Nonlinear State-space Identification of Hysteresis[J]. Mechanical Systems and Signal Processing, 2018, 104: 884-895.

[4] CHEN W, JANA D, SINGH A, et al. Measurement and Identification of the Nonlinear Dynamics of a Jointed Structure Using Full-Field Data, Part I: Measurement of Nonlinear Dynamics[J]. Mechanical Systems and Signal Processing, 2022, 166: 108401.

[5] JIN M, KOSOVA G, CENEDESE M, et al. Measurement and Identification of the Nonlinear Dynamics of a Jointed Structure Using Full-Field Data; Part Ⅱ-Nonlinear System Identification[J]. Mechanical Systems and Signal Processing, 2022, 166: 108402.

[6] CIVERA M, CALAMAI G, ZANOTTI FRAGONARA L. Experimental Modal Analysis of Structural Systems by Using the Fast Relaxed Vector Fitting Method[J]. Structural Control and Health Monitoring, 2021, 28(4): 2695.

[7] CIVERA M, CALAMAI G, FRAGONARA L Z. System Identification Via Fast Relaxed Vector Fitting for the Structural Health Monitoring of Masonry Bridges[J]. Structures, 2021, 30: 277-293.

[8] 朱大鹏. 随机振动条件下包装件动态特性识别方法[J]. 包装工程, 2017, 38(17): 96-101.

ZHU Da-peng. Dynamic Property Identification Method for Packages under Random Vibration[J]. Packaging Engineering, 2017, 38(17): 96-101.

[9] 朱大鹏. 包装系统非线性特性识别方法[J]. 包装工程, 2016, 37(21): 46-51.

ZHU Da-peng. Identification Method of Nonlinear Properties in Packaging System[J]. Packaging Engineering, 2016, 37(21): 46-51.

[10] FUENTES R, NAYEK R, GARDNER P, et al. Equation Discovery for Nonlinear Dynamical Systems: a Bayesian Viewpoint[J]. Mechanical Systems and Signal Processing, 2021, 154: 107528.

[11] SAFARI S, MONSALVE J L. Benchmarking Optimisation Methods for Model Selection and Parameter Estimation of Nonlinear Systems[J]. Vibration, 2021, 4(3): 648-665.

[12] GREEN P L, WORDEN K. Bayesian and Markov Chain Monte Carlo Methods for Identifying Nonlinear Systems in the Presence of Uncertainty[J]. Philosophical Transactions Series A, Mathematical, Physical, and Engineering Sciences, 2015, 373(2051): 20140405.

[13] CHIB S, GREENBERG E. Understanding the Metropolis-Hastings Algorithm[J]. The American Statistician, 1995, 49(4): 327-335.

[14] SPIEGELHALTER D J, BEST N G, CARLIN B P, et al. Bayesian Measures of Model Complexity and Fit[J]. Journal of the Royal Statistical Society: Series b, 2002, 64(4): 583-639.

[15] SPIEGELHALTER D J, BEST N G, CARLIN B P, et al. The Deviance Information Criterion: 12 Years on[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2014, 76(3): 485-493.

[16] WORDEN K. Data Processing and Experiment Design for the Restoring Force Surface Method, Part I: Integration and Differentiation of Measured Time Data[J]. Mechanical Systems and Signal Processing, 1990, 4(4): 295-319.

[17] WEN Y K. Method for Random Vibration of Hysteretic Systems[J]. Journal of the Engineering Mechanics Division, 1976, 102(2): 249-263.

Kinetic Package Model Optimal Selection Using Bayesian Inference

ZHU Da-penga, YU Zhena, CAO Xing-xiaob

(a. School of Traffic and Transportation, b. School of Mechanical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

The work aims to select the optimal model from various models and achieve parameter identification. The package model was constructed as the parameter uncertainty model. The model parameters were identified with the Markov Chain Monte Carlo method in Bayesian inference framework. Deviation information criterion (DIC) was used to calculate the DIC parameters of each alternative model and select the optimal package model. The mass block-buffer material was used to simulate the package and the random vibration test was carried out on the vibration test bench. The analysis result showed that the Bouc-Wen model (=2) was the optimal model for the package. The model selection and parameter identification method proposed based on Bayesian inference takes the uncertainty of the model into account. The constructed model can accurately predict the time-domain signal of acceleration response of the package under random vibration.

model selection; Bayesian inference; Markov Chain Monte-Carlo (MCMC); Metropolis-Hastings algorithm; deviance information criterion (DIC)

TB485.3

A

1001-3563(2023)05-0238-06

10.19554/j.cnki.1001-3563.2023.05.030

2022–10–10

甘肃省自然科学基金（20JR5RA400）；兰州交通大学–天津大学联合创新基金项目（2022063）

朱大鹏（1977—），男，博士，教授，主要研究方向为运输包装、运输安全。

责任编辑：曾钰婵