基于新型趋近律的永磁同步电机动态性能优化

董洪昭，杜秋月，刘珂，姚淇，詹伟梁

自动化与智能化技术

基于新型趋近律的永磁同步电机动态性能优化

董洪昭，杜秋月，刘珂，姚淇，詹伟梁

（北京工商大学，北京 100048）

提高永磁同步电机作业时的响应精度和速度，优化其动态反馈性能，解决传统滑模控制中趋近时间与系统抖振相矛盾的问题。采用三闭环控制结构，位置环与电流环采用模糊PID控制方法，速度环采用基于新型趋近律的改进滑模控制方法，添加扰动观测器并给予系统扰动补偿。仿真与在环硬件测试结果表明，文中提出的控制方法与传统三闭环滑模控制相比，相同时间内电机转子位置响应速度提前了0.123 s且无超调，同时明显降低了电磁转矩波动幅度。文中设计的新型趋近律有效改善了传统滑模控制存在的问题，建立的控制系统有效提高了永磁同步电机的响应精度和速度，削弱了永磁同步电机作业时的抖振程度，具有良好的鲁棒性。

永磁同步电机；三闭环控制；新型趋近律；动态优化

随着科技和经济快速发展，永磁同步电机在食品包装、药品包装等领域得到了广泛应用，多行业对产品包装的生产效率及精度需求日益增加，这为包装工业机械向全自动化、智能化方向发展开拓了巨大的空间。在该行业中，越来越多的企业采用永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）取代传统的步进电机[1-3]。虽然永磁同步电机具有工作效率高、无励磁损耗等优点，但是由于电机本身在产品加工过程中会因负载变化和参数摄动而不可避免地产生抖振现象，故由其驱动的包装、运输等机械通常存在对材料运送速度控制精度低、抗扰性能弱等问题，影响生产效率和精度。为解决此问题，越来越多的学者开始关注永磁同步电机的优化控制。

随着工业生产对永磁同步电机工作性能的要求越来越严格，传统纯PID控制已无法满足高精度生产要求[4]，因此，很多非线性的控制方法开始被广泛应用于PMSM的控制中，比如模糊控制、滑模变结构控制、神经网络控制等。熊新国等[3]分析了影响包装机材料供送速度控制精度的因素，通过设计双模糊PID控制策略，提升了包装材料供送速度控制的稳定性和控制精度。许馨尹等[5]采用模糊自适应PID控制方法，结合电压前馈解耦的优化策略，实现了永磁同步电机的自适应闭环控制。赵潮等[6]采用三闭环控制方法，在位置环使用模糊自适应PID控制器，验证了在三闭环控制中模糊PID控制比传统PID控制鲁棒性更强的优点。此外，滑模控制也被广泛应用于调速系统，研究学者通过设计不同趋近律来减小滑模抖振，大大提高了速度跟踪精度[7-9]。祝新阳等[10]设计了一种改进滑模观测器的PMSM矢量控制方法，用于更准确地对电机的反电动势和转子位置进行观测，但是在转速环的设计中滑模参数不易调节。扶文树等[11]设计了一种基于高增益扩张观测的扰动反馈线性化控制器，用于永磁同步电机转速控制，实验结果证明，该设计方法对转速突变和外部负载扰动有较好的鲁棒性，但去噪效果仍有待改善。Cao等[12]通过设计扩张状态观测器来估计扰动，在滑模控制律中消除抖振，但系统趋近时间有所延长。李绍民等[13]针对装填机械提出了一种新型自适应滑模控制方法，通过梯形速度曲线规划算法实现了较高精度的位置跟踪。综上，在PMSM的三闭环控制中，模糊控制在位置环、电流环有着较好的控制效果，而滑模控制在速度环虽有良好的速度调节功能，但系统抖振与趋近时间相矛盾的问题仍有待改进。

为此，文中针对PMSM因负载变化和内外扰动产生的抖振现象进行分析，采用三闭环控制方法，结合模糊PID与改进新型滑模控制，从响应精度、速度、削弱抖振能力的提升三方面进行PMSM动态反馈性能的优化实验。通过设计基于新型趋近律的速度滑模控制器和扰动补偿器，减小控制增益，抑制滑模抖振。在设计的新型趋近律中添加终端项以解决系统抖振和滑模面趋近时间的矛盾，进一步提高系统的鲁棒性。

1 建立永磁同步电机数学模型

为使电机系统便于分析，作如下几点假设：忽略电机铁芯的饱和；不计涡流和磁滞损耗；电机中的电流为对称的三相正弦波电流。

永磁同步电机在三相静止坐标系中的电压、磁链方程可表达为：

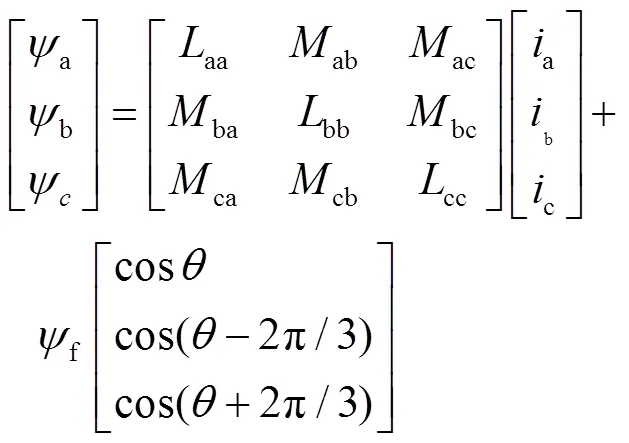
式中：abc为三相电压；abc为三相电流；a、b、c为三相磁链；s为定子电阻；、分别为自感和互感；f为转子磁链；为转子磁极位置。

经过Clark、Park变换，可以得到PMSM在同步旋转坐标系–轴中的电压方程：

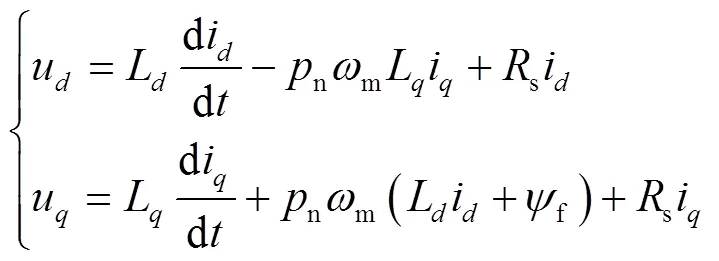
磁链方程：

电磁转矩方程：

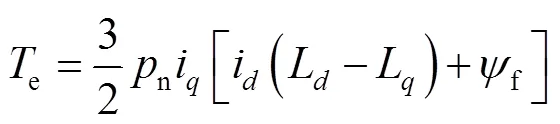
式中：e为电磁转矩；m为电机实际转速；、、、分别为定子电压和定子电流在–坐标系的分量；、为–轴电感分量；n为极对数。文中以表贴式PMSM为研究对象，采用=0的控制方法来定向控制转子磁场，则=L，电磁转矩方程：

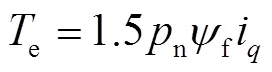
电机运动方程：

式中：L为负载转矩；为阻尼系数；为电机的转动惯量。

2 三闭环矢量控制系统

通过控制电机定子电流在同步旋转坐标系中的大小和方向，实现磁场和转矩的解耦控制及转矩线性化控制，达到对直轴和交轴分量解耦的目的。三闭环控制系统由电流环、速度环、位置环、空间矢量脉宽调制（SVPWM）算法和坐标变换等模块组成，三闭环矢量控制系统原理见图1，其中电流环和位置环均采用模糊PID控制，速度环采用基于新型趋近率的自适应滑模控制。

2.1 新型趋近率设计

在传统滑模控制器的设计中，通常采用指数趋近率：

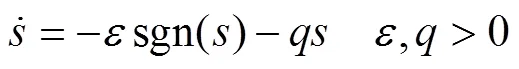
速度滑模控制律一般设计为：

传统控制律中非连续项sgn()会导致系统产生抖振，并且值决定了抖振的程度。和的取值越大，系统收敛速度越快，但抖振程度也会越剧烈；如果值减小，可以削弱系统抖振程度，但滑模面趋近时间会延长，鲁棒性降低[14]。为改善抖振与趋近时间相互冲突的缺点，结合文献[9]设计了一种新型趋近律：

饱和函数()为：

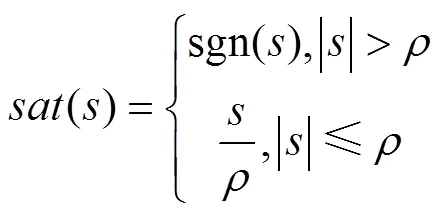
式中：1>0，t>0，2>0，>0，0<<1，0<<2，0<<1；为滑模面；为系统状态变量；为函数边界层值。当||较大时，该趋近律等速项系数大于初始增益1，即系统离滑模面越远，趋近滑模面的速度就越大，确保系统能快速趋于稳定状态，加入的终端项t||，可使系统在||值比较大的情况下，有更好的动态反馈响应，有效降低系统抖振程度[15]。当||趋近于0时，等速项系数小于初始增益1，即系统越来越趋近滑模面时，速度会越来越小，系统状态变量||也会逐渐趋近于0。

对该新型趋近律进行稳定性分析，构建Lyapunov函数如下：

对求导，得：

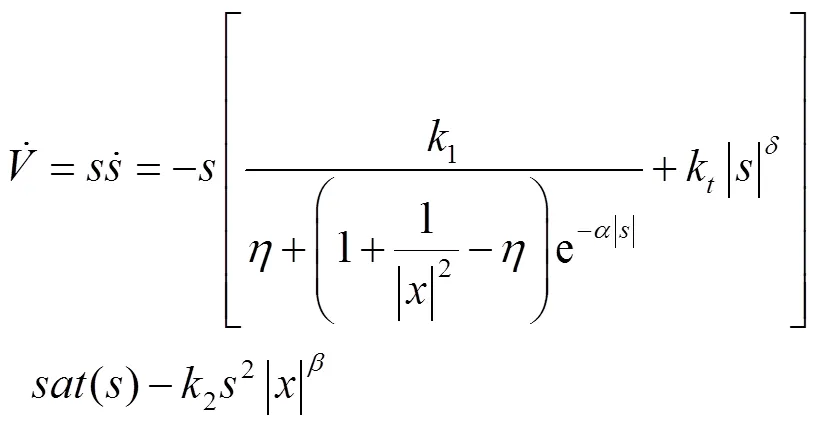
因为()>0，+(1+1/||2−)e−α|s|>0，故式（13）小于0成立，所以该新型趋近律在Lyapunov意义下是可收敛的，具有稳定性。

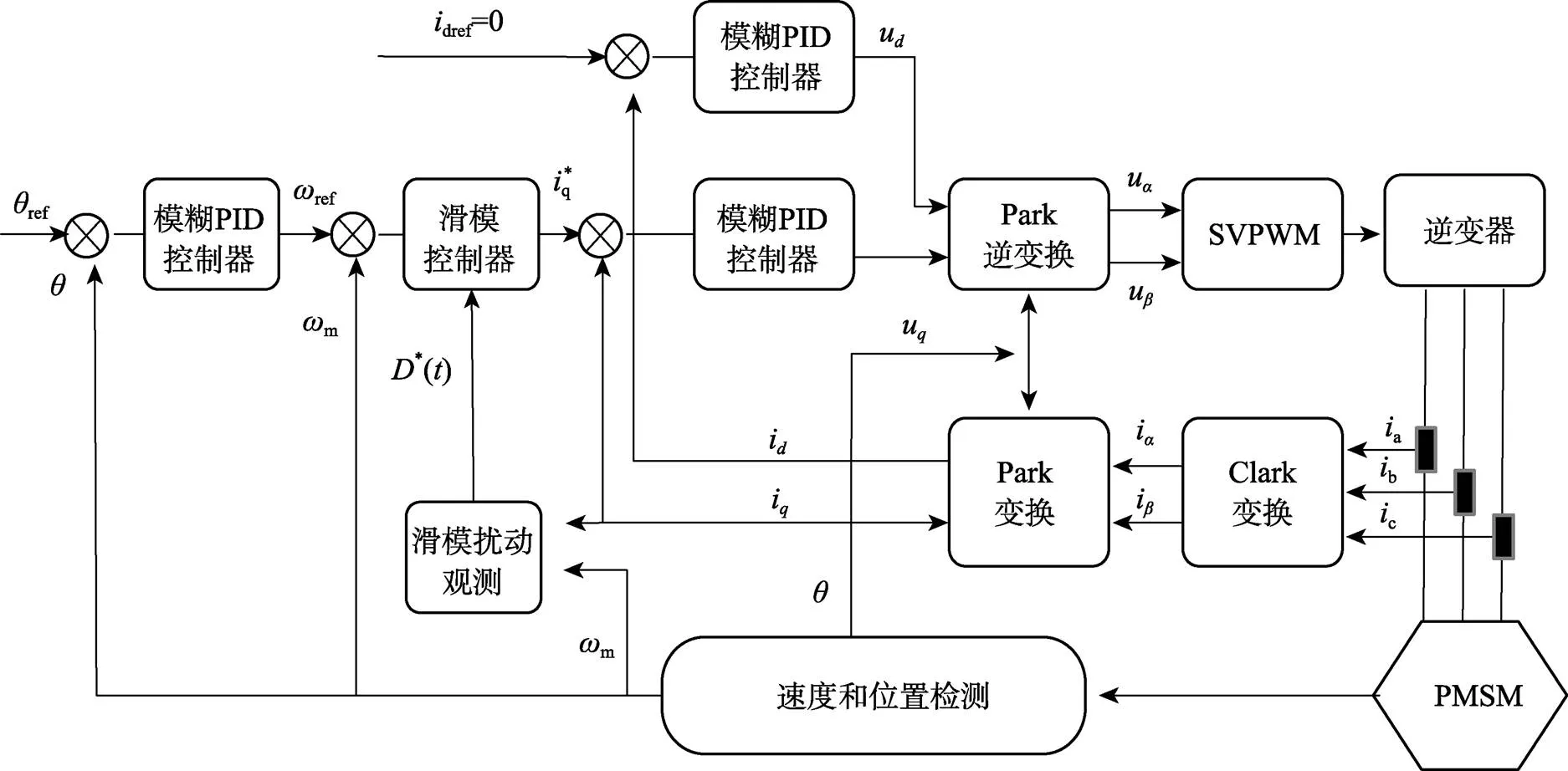
图1 三闭环矢量控制系统

2.2 滑模速度控制器设计

鉴于滑模控制具有对扰动与参数不敏感、响应速度快等优点，所以速度环控制器采用滑模控制方法，可有效提高三相PMSM调速系统的动态品质。

定义速度误差：

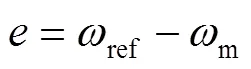
选用积分滑模面可避免出现变量的二阶导数及稳态误差[16]：

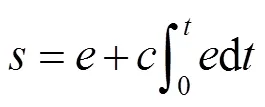
式中：为待设计的积分系数。考虑负载扰动及内部参数变化影响，设()为负载与参数变化带来的总扰动，结合式（7）可得：

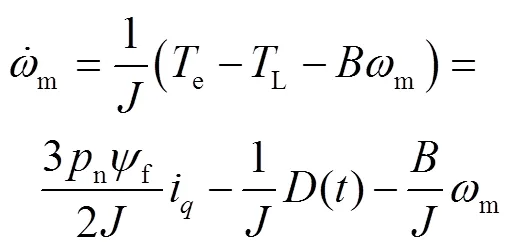
结合式（10），作如下简化：

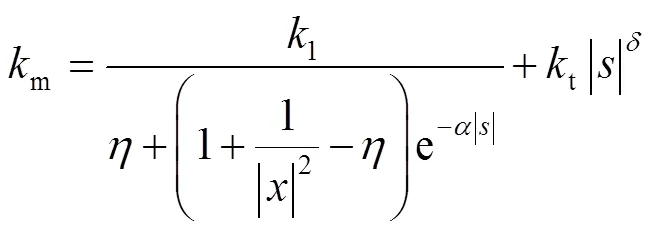
则轴的参考电流表达式：

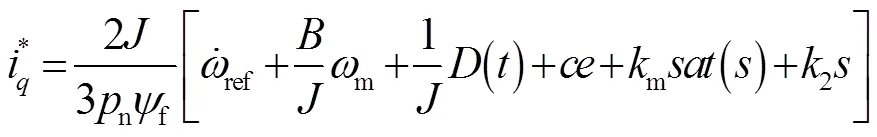
为验证控制器稳定性，定义Lyapunov函数：

结合式(13)、式(16)—(19)可得：

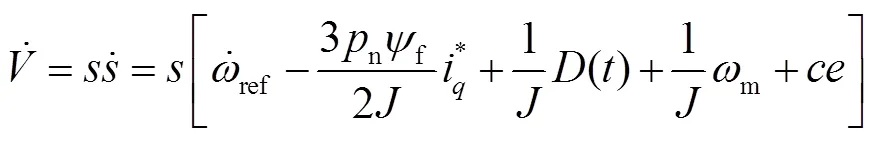
由式（21）—（22）可得：

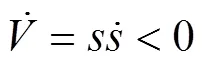
根据Lyapunov稳定性理论推导结果，可证得采用该滑模控制器后，系统的速度跟踪误差可以在有限时间内趋近于0，系统稳定。

2.3 设计扰动补偿器

在实际应用中，控制系统的状态轨迹到达滑模面后，是在滑模面两侧来回穿越而非严格地沿着滑模面向平衡点移动，因此抖振必定存在且无法消除。为进一步削弱抖振程度，设计一个滑模扰动补偿器，实时观测外部扰动带给系统的影响并给予前馈扰动补偿。

取电磁转矩e作为输入，机械角速度m、扰动作为系统状态变量，建立系统状态空间方程：

将机械角速度m和扰动作为观测对象，由式（24）可得扰动补偿方程：

由式（24）、（25）可得扰动补偿的误差方程：

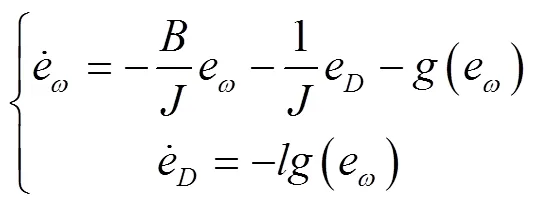
式中：为观测的速度误差；为扰动误差；()为针对的滑模控制律；为()的增益。为使扰动补偿误差趋近于0，取值应小于0，经测试取值应为−2.5。

选取滑模面：

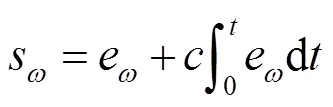
选用趋近律：

将−/项作为扰动项，结合式（26）、（28）、（29）可设计滑模扰动补偿器的控制律为：

为验证该控制律稳定性，定义Lyapunov函数为：

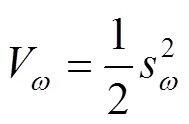
对进行求导，可得：

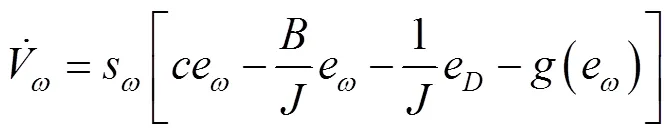
根据李雅普诺夫稳定性理论，为确保滑模面存在且可达，需满足：

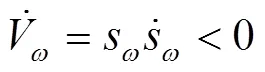
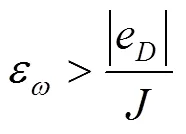
式（34）表明，切换增益的取值与扰动误差直接相关。为避免过大而导致抖振加剧，将设计为的函数形式：

式中：为大于1的常数。系统观测到扰动值*后，产生扰动误差，扰动误差越大，增益相应也增大，实时保证系统的稳定性。经扰动补偿后，扰动误差逐渐趋近于0，此时增益也趋近于0，可实现对系统因外部干扰所产生抖振的削弱。通过扰动补偿反馈到滑模控制器的输出端，结合式（19）可得速度滑模控制律为：

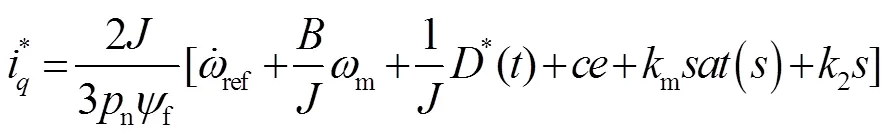
由式（36）可看出，当系统出现扰动时，扰动值作为常量反馈到控制律中，通过电流环控制算法，可实现微小的控制增益，便能提高系统动态响应精度，达到调整转矩矢量变化的目的，有效降低电磁转矩的波动幅度，削弱抖振程度，保证系统稳定运行。

3 仿真与实验

3.1 仿真模型

为验证上述设计方法的可行性，在Matlab/Simulink软件中搭建仿真模型，建立滑模控制器、扰动补偿器及三闭环控制结构模型，见图2—4。

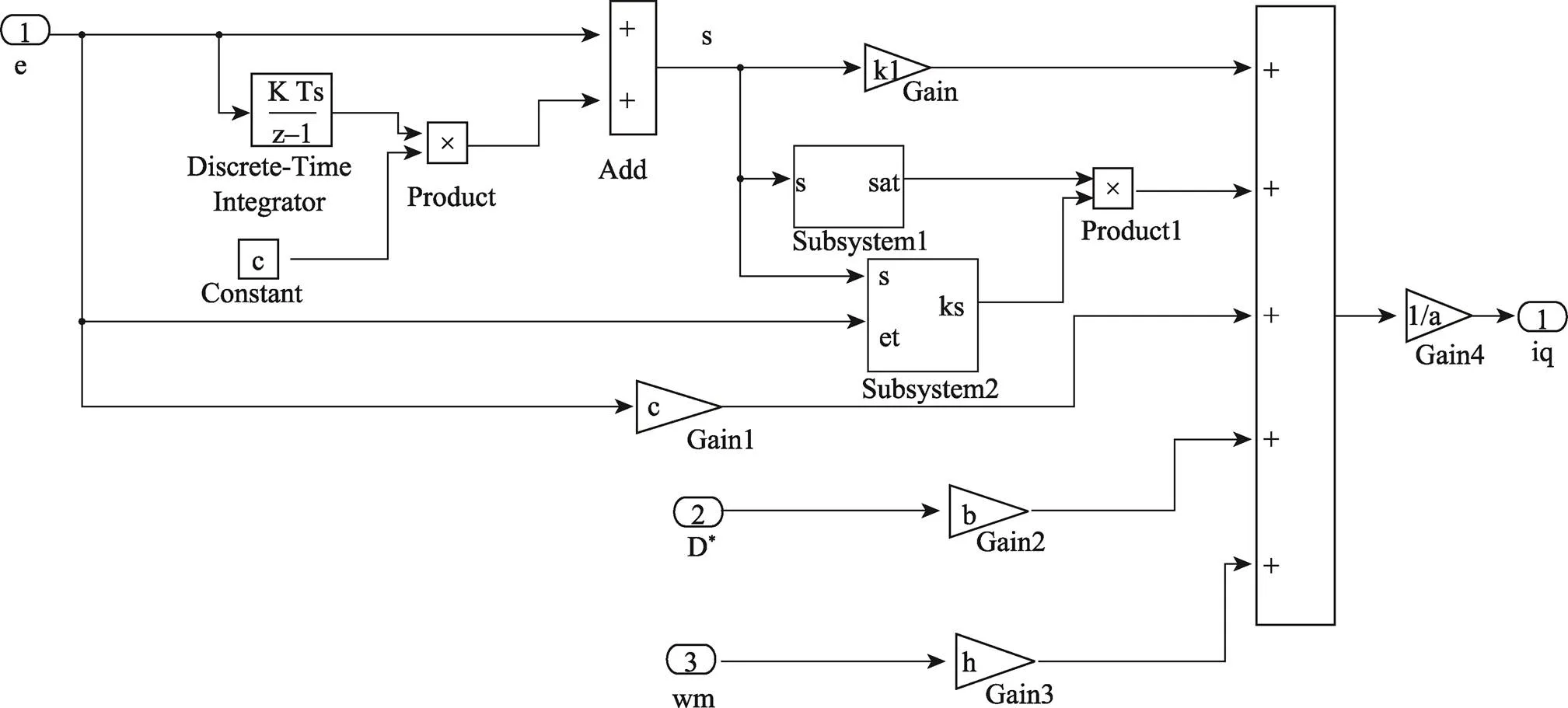
图2 滑模控制器结构

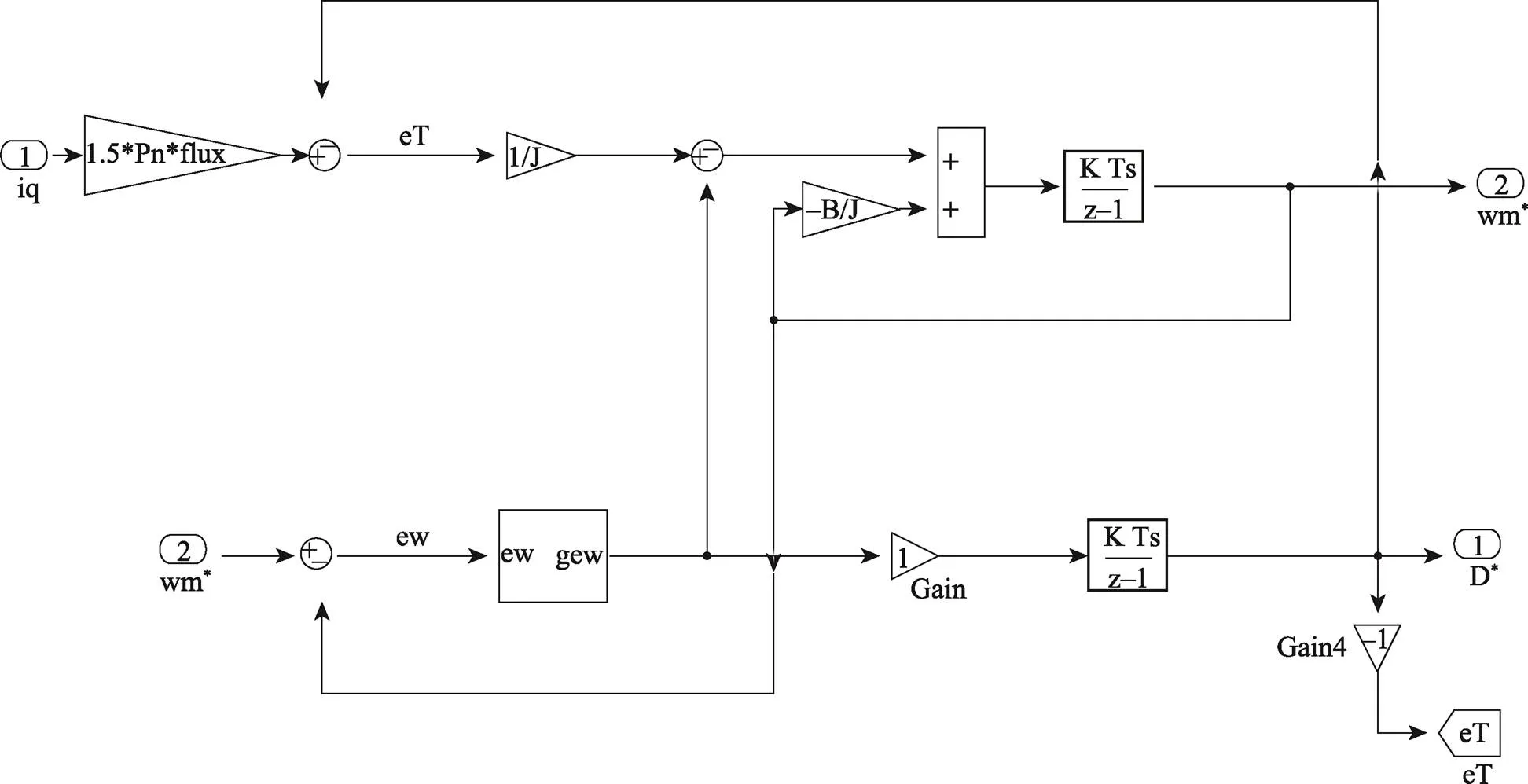
图3 扰动补偿器结构

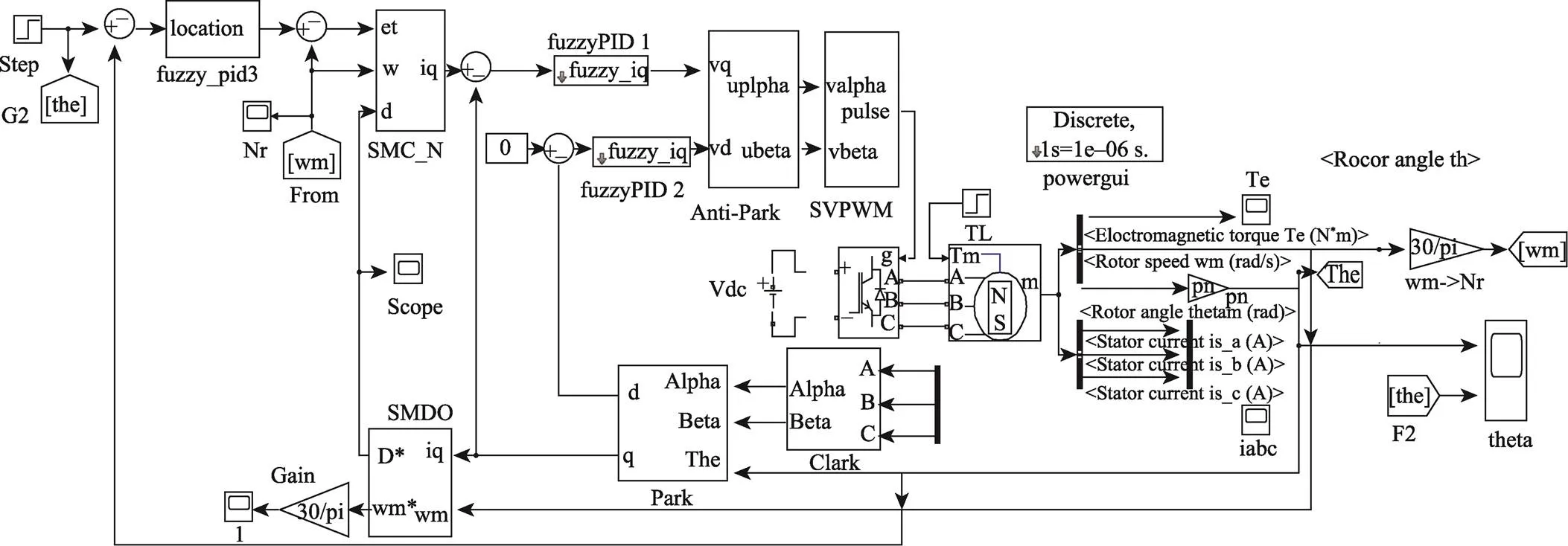
图4 三闭环控制模型

3.2 在环实物平台

在环实物测试平台中，选用隐极式永磁同步电机作为实物电机，具体参数见表1。扭矩传感器型号为HCNJ−101，扭矩输出频率为5～15 kHz，转速为0～6 000 r/min。每次上电后，进行零位标定，以消除初始误差，在环实物测试平台见图5。通过电机夹具固定实物电机，防止测试过程中因外部干扰而产生位置变化，通过上位机与控制器发送控制命令，使用扭矩传感器来观测电机负载转矩变化。

表1 选用电机参数

Tab.1 Selection of motor parameters

图5 在环实物测试平台

3.3 实验结果分析

仿真条件设置：直流侧电压dc=311 V，设置PWM开关频率pwm=10 kHz，设置采用周期s=10 μs，采用变步长ode23tb算法，仿真时间为0.7 s。

仿真工况设置如下：

1）设定电机初始时刻负载为2 N·m，在0.4 s时阶跃为8 N·m；设定初始时刻转角给定值分别为8π，在0.4 s时阶跃为12π。

2）负载设定与1相同，初始启动与运行4 s时的给定位置转角分别设为16π、24π。

为验证新型趋近律的可行性和优越性，在电流环和位置环均采用模糊PID控制且参数相同的前提下，将基于新型趋近律的滑模观测控制（NSMC）与传统滑模控制（SMC）的各项性能进行仿真对比，通过控制器及信号接收器观察电机转子转角跟随情况，以及在有无扰动观测器的2种工况下的转矩实际变化。转角位置跟踪实验结果见图6—7。

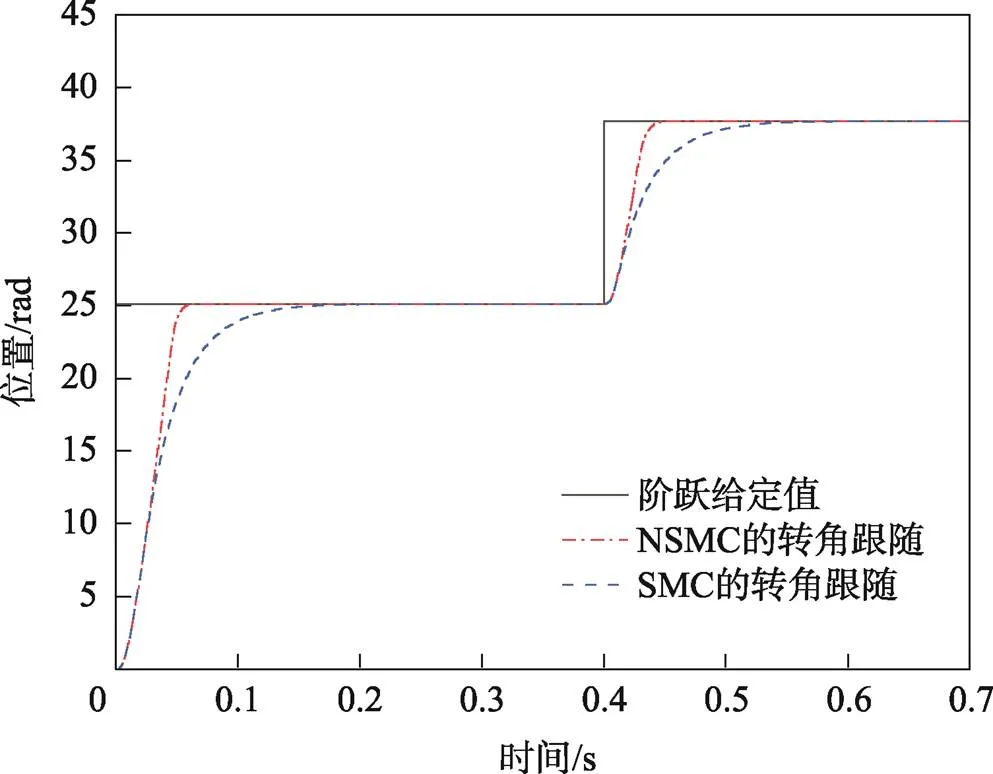
图6 工况1下的位置阶跃响应曲线

图7 工况2下的位置阶跃响应曲线

扭矩传感器观测负载转矩变化结果如图8所示。

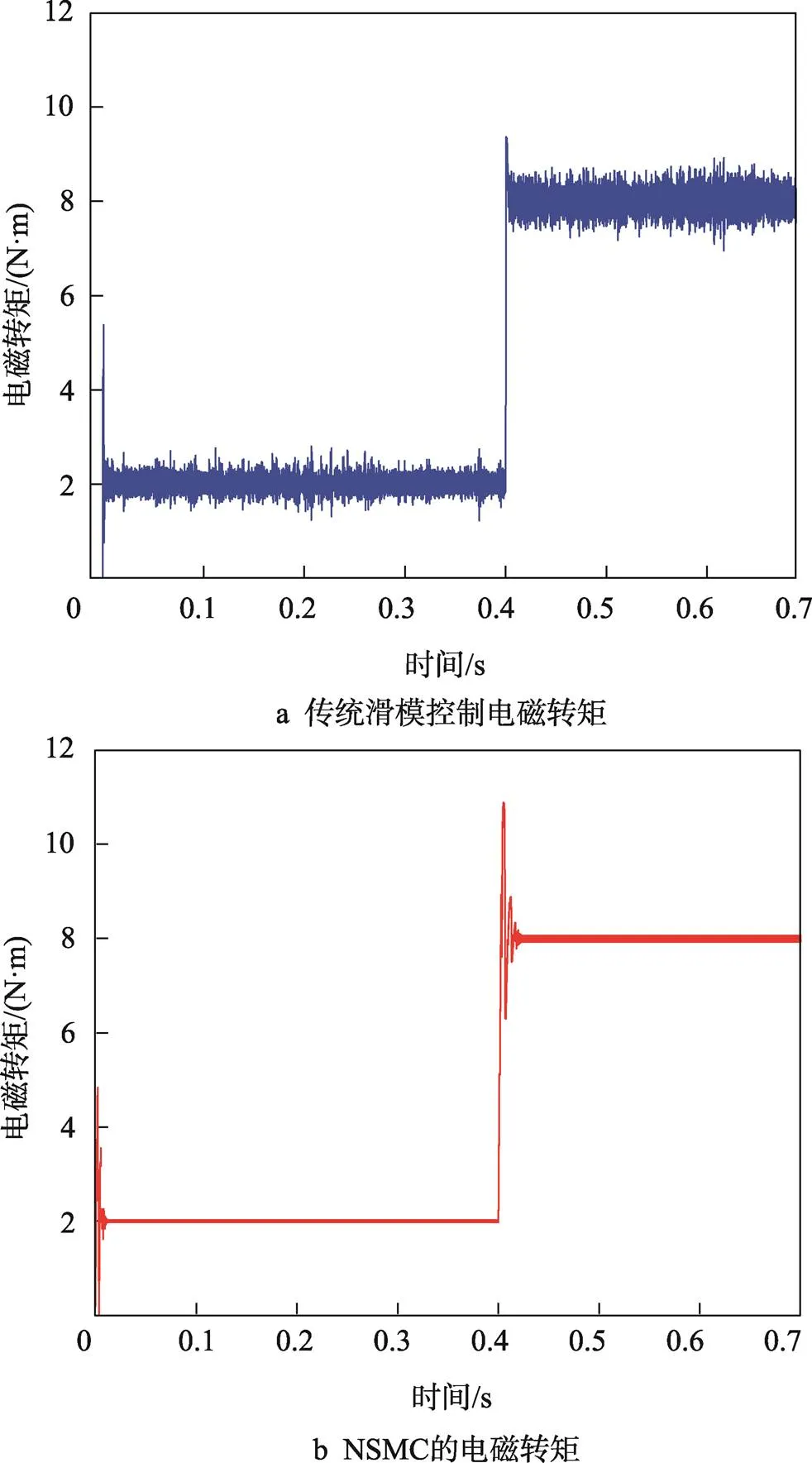
图8 负载突变时转矩传感观测结果

由图6、图7可知，工况1的位置跟踪初始阶段，SMC条件下电机转子在0.188 s到达指定位置，而NSMC条件下电机转子在0.065 s到达指定位置；给定位置阶跃后，SMC条件下电机转子在0.565 s到达指定位置后稳定，而NSMC条件下电机转子在0.45 s即达到稳定。工况2，SMC与NSMC在位移跟踪时，到达稳态时间相近，但传统滑模控制下的电机出现了位置超调，超调量超过了2%且伴有轻微抖振；而NSMC下的电机响应平稳，无超调。由图8可知，当负载突变时，相较于传统滑模闭环控制，NSMC方法使电机的转矩波动范围更小，且去噪效果更加良好。综上，相较传统三闭环滑模控制，NSMC方法的位置响应更迅速，没有超调量，电磁转矩扰动小、抖振抑制能力强、跟踪效果也更精准，有效验证了该新型趋近律及扰动补偿下的滑模控制具有更好的鲁棒性和可行性。

4 结语

文中提出的永磁同步电机控制方法获得了良好的控制效果，有效提高了电机响应速度，降低了电磁转矩波动幅度。其中，将所设计的新型趋近律应用至速度环滑模控制器，并通过在新型趋近律中添加终端项进一步削弱了系统抖振程度。同时给予系统前馈补偿能力，通过实时扰动反馈与补偿，进一步提高了系统的动态性能和稳定性。通过仿真与在环硬件测试，验证了文中提出的新型趋近率及控制方法，能够有效提高电机转子响应速度并削弱抖振，改善永磁同步电机的实时动态反馈性能，具有更加良好的响应性能和鲁棒性。PMSM在转矩控制方面仍有较大的研究价值和改进空间，未来将结合模型预测控制、神经网络控制等先进控制方法继续展开深入探索研究。

[1] 吴祥瑞. 立式包装机用永磁同步电机控制系统设计[D]. 镇江: 江苏科技大学, 2017: 13—18.

WU Xiang-rui. Design of Permanent Magnet Synchronous Motor Control System for Vertical Packaging Machine[D]. Zhenjiang: Jiangsu University of Science and Technology, 2017: 13-18.

[2] 王都阳, 张建昌. 药品包装机人机工程系统与评价[J]. 包装工程, 2019, 40(21): 187-192.

WANG Du-yang, ZHANG Jian-chang. Ergonomic System and Evaluation of Pharmaceutical Packaging Machine[J]. Packaging Engineering, 2019, 40(21): 187-192.

[3] 熊新国, 郝军, 刘拥军. 基于双模糊PID的枕式包装机材料供送速度控制方法[J]. 包装工程, 2021, 42(17): 255-260.

XIONG Xin-guo, HAO Jun, LIU Yong-jun. Control Method of Material Supply Speed of Pillow Packing Machine Based on Double Fuzzy PID[J]. Packaging Engineering, 2021, 42(17): 255-260.

[4] 余鑫, 王兵, 刘凯, 等. 基于滑模观测器的永磁同步电机无位置传感器控制研究[J]. 湖南工业大学学报, 2020, 34(6): 1-9.

YU Xin, WANG Bing, LIU Kai, et al. Research on the Sensorless Control of Permanent Magnet Synchronous Motor Based on Sliding Mode Observer[J]. Journal of Hunan University of Technology, 2020, 34(6): 1-9.

[5] 许馨尹, 孙光. 基于自适应模糊PID的PMSM矢量控制系统研究[J]. 中国高新科技, 2019(10): 18-19.

XU Xin-yin, SUN Guang. Research on PMSM Vector Control System Based on Adaptive Fuzzy PID[J]. China High-Tech, 2019(10): 18-19.

[6] 赵潮, 刘家国, 唐煜. 基于simulink的模糊自适应PID三闭环控制设计及仿真[J]. 数字技术与应用, 2019, 37(10): 1-4.

ZHAO Chao, LIU Jia-guo, TANG Yu. Design and Simulation of Fuzzy Self-Adaption PID Three Closed Loop Control Based on Simulink[J]. Digital Technology and Application, 2019, 37(10): 1-4.

[7] ZHANG Xiao-guang, LI Zheng-xi. Sliding-Mode Observer-Based Mechanical Parameter Estimation for Permanent-Magnet Synchronous Motor[J]. Transactions on Power Electronics, 2016, 31(8): 5732-5745.

[8] WANG Ai-meng, WEI Sheng-jun. Sliding Mode Control for Permanent Magnet Synchronous Motor Drive Based on an Improved Exponential Reaching Law[J]. Access, 2019 (99): 1.

[9] ZHANG Li-wei, LI Hang, SONG Pei-pei, et al. Sensorless Vector Control Using a New Sliding Mode Observer for Permanent Magnet Synchronous Motor Speed Control System[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 70-78.

[10] 祝新阳, 曾国辉, 黄勃, 等. 改进滑模观测器的永磁同步电机矢量控制[J]. 信息与控制, 2020, 49(6): 708-713.

ZHU Xin-yang, ZENG Guo-hui, HUANG Bo, et al. Vector Control for Permanent Magnet Synchronous Motor Based on Improved Sliding Mode Observer[J]. Information and Control, 2020, 49(6): 708-713.

[11] 扶文树, 储建华, 王刚. 永磁同步电机转速环扰动反馈线性化控制[J]. 电气传动, 2021, 51(24): 27-32.

FU Wen-shu, CHU Jian-hua, WANG Gang. Disturbance Feedback Linearization Control for Permanent Magnet Synchronous Motor Speed Loop[J]. Electric Drive, 2021, 51(24): 27-32.

[12] CAO Song-yin, LIU Jun, YI Yang. Non-Singular Terminal Sliding Mode Adaptive Control of Permanent Magnet Synchronous Motor Based on a Disturbance Observer[J]. The Journal of Engineering, 2019(15): 629-634.

[13] 李绍民, 徐亚栋, 邹权, 等. 基于新型趋近律的装填机械手自适应滑模控制[J]. 火炮发射与控制学报, 2022, 43(3): 68-73.

LI Shao-min, XU Ya-dong, ZOU Quan, et al. Adaptive Sliding Mode Control of a Loading Manipulator Based on a New Approach Law[J]. Journal of Gun Launch & Control, 2022, 43(3): 68-73.

[14] ZHANG Xiao-guang, SUN Li-zhi, ZHAO Ke, et al. Nonlinear Speed Control for PMSM System Using Sliding-Mode Control and Disturbance Compensation Techniques[J]. Trans Power Electron, 2013, 28(3): 1358-1358.

[15] 刘京, 李洪文, 邓永停. 基于新型趋近律和扰动观测器的永磁同步电机滑模控制[J]. 工程科学学报, 2017, 39(6): 933-944.

LIU Jing, LI Hong-wen, DENG Yong-ting. PMSM Sliding-Mode Control Based on Novel Reaching Law and Disturbance Observer[J]. Journal of University of Science and Technology Beijing, 2017, 39(6): 933-944.

[16] 李政, 胡广大, 崔家瑞, 等. 永磁同步电机调速系统的积分型滑模变结构控制[J]. 中国电机工程学报, 2014, 34(3): 431-437.

LI Zheng, HU Guang-da, CUI Jia-rui, et al. Sliding-Mode Variable Structure Control with Integral Action for Permanent Magnet Synchronous Motor[J]. Proceedings of the CSEE, 2014, 34(3): 431-437.

Dynamic Performance Optimization of Permanent Magnet Synchronous Motor Based on New Reaching Law

DONG Hong-zhao, DU Qiu-yue, LIU Ke, YAO Qi, ZHAN Wei-liang

(Beijing Technology and Business University, Beijing 100048, China)

The work aims to improve the response accuracy and speed of the permanent magnet synchronous motor during operation and optimize its dynamic feedback performance, to solve the problem of the contradiction between the reaching time and the system jitter in the traditional sliding mode control. In the experiment, a three-closed-loop control structure was used, in which a fuzzy PID control method was adopted for the position loop and current loop, and an improved sliding mode control method based on the new reaching law was adopted for the speed loop. Then, a disturbance observer was applied and the disturbance compensation was given to the system. According to the simulation results and the in-the-loop hardware test results, compared with the traditional three-closed-loop sliding mode control, the rotor position response speed of the proposed control method was 0.123 seconds faster and there was no overshoot within the same time, and the electromagnetic torque fluctuation amplitude was significantly reduced. The new reaching law designed effectively solves the problems existing in the traditional sliding mode control, and the established control system effectively improves the response accuracy and speed of the permanent magnet synchronous motor, weakens the jitter degree of the PMSM during operation, and provides good robustness.

PMSM; three-closed-loop control; new reaching law; dynamic optimization

TB486

A

1001-3563(2023)05-0163-08

10.19554/j.cnki.1001-3563.2023.05.021

2022−04−02

国家自然科学基金青年基金项目（51805009）；2022年研究生科研能力提升计划项目

董洪昭（1999—），男，硕士生，主攻智能汽车线控技术、电机驱动控制及应用。

杜秋月（1987—），女，博士，副教授，主要研究方向为仿生机械设计及制造、智能汽车技术。

责任编辑：曾钰婵