一种基于分段线性混沌映射的医学图像加密算法

秦秋霞，梁仲月，徐 毅

(大连民族大学 a.计算机科学与工程学院；b.理学院 预科教育学院，辽宁 大连 116650)

随着医疗水平高速发展，人口老龄化的急剧增长。医学图像信息得到大范围的使用，面对海量、冗余度高的医学图像信息，寻找更加安全、有效的医学图像信息加密算法是十分重要的[1-3]。为了保证医学图像信息传输的安全性，防止出现个人、相关机构及国家医疗信息的泄露，本文提出了一种基于分段线性混沌映射的医学图像加密算法，通过使用多轮加密的方式，实现了医学图像的加密，提高了医学图像加密算法的安全性和鲁棒性。

混沌系统一般指的是一种非常复杂、并且不能依据初始状态用来预测将来状态的具有很大随机性的系统[4-5]。同时，混沌系统敏感性的特征十分符合加密算法的要求，适用于扩散和置乱过程。纪等人[6]提出了一种基于混沌的新型舰船安全图像加密算法，使用混沌置乱实现置乱操作，提高加密安全性；乔等人[7]为了解决传统加密步骤繁琐的问题，提出了一种基于二维Logistic混沌系统的图像加密算法，使用混沌序列改变像素值的位置，该算法加密效果良好；张等人[8]提出了结合S盒与混沌映射的图像加密算法，使用二维Logistic映射和Chen混沌系统生成的混沌序列参与置乱、扩散过程，提高了加密效果；杜等人[9]提出了基于混沌压缩感知和DNA编码的多图像加密算法，混沌系统使用Lorenz超混沌系统和Chen超混沌系统，产生随机性更强的混沌序列，实现了一次一密的加密方式。从仿真结果和安全性分析结果可以看出，将混沌系统引入图像加密算法可以使得加密效果更加优越，加密算法的随机性和健壮性更有保证。

本文使用的混沌映射是PWLCM混沌映射，PWLCM混沌映射是一种分段线性混沌映射，它具有良好的遍历性和很少的周期窗口等特点[10-12]。混沌现象是发生在确定系统中的不确定行为。使用分段线性混沌映射可以实现医学图像中稳定状态和不稳定状态之间的转换。PWLCM混沌映射的初值敏感性符合加密算法的扩散操作，而随机特性符合加密算法的置乱操作，因此分段线性混沌系统十分符合加密算法的要求。由于PWLCM混沌映射在加密算法中具有较高的应用效果，因此本文将其引入到医学图像加密算法中。

医学图像加密算法不仅可以对普通图像进行加密，还可以对医学图像进行加密。医学图像加密需要尽可能的保证加密过程的安全性，保护病患的隐私信息；另外，还需要保证解密后的得到的图像可以达到医生诊断的正常需求。依据上述问题以及分析，本文提出了一种基于分段线性混沌映射的医学图像加密算法。本算法采用四轮加密的方式，增强算法的安全性，使用分段线性混沌映射参与每一轮的置乱和扩散过程，提高算法的随机性。每一轮的置乱过程都采取随机数插入的方式进行，扩散过程采用按位异或的方式来实现，每一轮结束后进行矩阵旋转然后再继续进行下一轮加密。当四轮加密结束后，得到加密图像，完成整个加密过程。

本文剩余章节的结构如下：第一部分主要介绍本算法使用的基本理论；第二部分介绍加、解密算法的流程和详细步骤；第三部分给出加密算法的仿真实验和安全性分析结果；第四部分给出结论。

1 基本原理

本章主要介绍本文用到的分段线性混沌映射，医学图像相关原理。

1.1 分段线性混沌映射

分段线性混沌映射(PWLCM)是一种常见的分段混沌映射。由于其具有周期窗口小、遍历性好、生成混沌序列分布均匀等特性，研究人员将其应用于图像加密领域[10-11,13]。PWLCM混沌映射定义如下：

(1)

式中：x是系统参数；r是控制参数，x∈(0,1)。当r∈(0,0.5)时，系统处于混沌状态。PWLCM混沌映射具有一致的变量分布和较好的遍历性，可以提供满足加密算法随机性的随机序列，并且简单容易实现，适合用于图像加密领域。

1.2 医学图像

医学图像是医护人员进行医疗诊断工作的主要参考数据之一，它是通过医疗器材获取的人体某一部位的图像信息[14-15]。医学图像信息能够直观地反映人体某一部位是否存在病变，而且医学图像在不同的场景下应用时对图像分辨率有着不同的要求。当医生使用医学图像用来判断病人的身体状况时，此时要求医学图像必须具有高分辨率；当医学图像用于病历分析时，可以容忍医学图像存在一定程度的损失压缩，以达到节省存储空间的作用。但不论哪种情况，在使用医学图像时，必须保证医学图像具有较高的分辨率，并且在传输过程中要做到足够的安全性，以避免病人隐私的泄露。在临床应用中，医学图像主要有为X-射线图像、CT、核磁共振成像等类型[16-17]如图1。

a) Brain b) Chest c) Tibial

2 加解密算法

本文提出了一种基于分段线性混沌映射的医学图像加密算法。首先，对原始图像进行随机数的插入。其次，使用分段线性混沌映射替换图像矩阵的像素值，实现置乱操作。然后，将替换后的矩阵与未进行替换前的矩阵进行按位异或操作，实现像素值的改变。最后，将第一轮结束后的矩阵逆时针旋转90度，继续进行下一轮加密操作，经过四轮加密后生成加密图像，加密结束。多轮加密和分段线性映射的使用确保加密算法的安全性，可用于医学图像加密。具体的加密步骤如2.1～2.3节所示。加密流程图如图2。

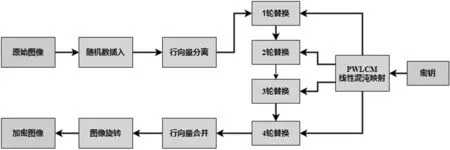
图2 加密流程图

2.1 随机数插入

在原始图像P中插入一列随机值，为后续替换和扩散操作做准备，具体如下：

第一步：读取原始图像P，原始图像的长是M，宽是N。

第二步：采用双层循环的方式生成随机数插入后的矩阵R，R的大小是M×(N+1)。其中，R矩阵的第1列元素是通过随机数函数randi()生成的，其他列的元素是原始图像的各个像素值。具体如下：

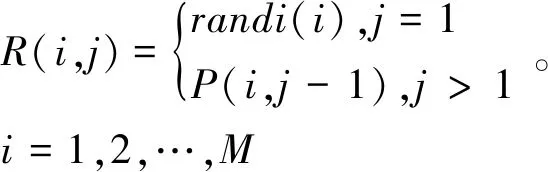
(2)

其中，randi()函数用于生成均匀分布的伪随机整数。

2.2 第一轮加密

本加密算法总共采用四轮加密，每一轮加密都是类似的，下面以第一轮加密为例进行详细的介绍。首先，对随机数插入后的矩阵R使用分段线性映射进行替换操作，然后将替换后的矩阵进行按位异或操作，最后将得到的矩阵进行矩阵的旋转，继续进行下一轮的加密，直到第四轮加密结束，完成加密。

2.2.1 替换操作

整个替换过程分为两个部分，先对第1列的元素进行替换，再对其他元素进行替换，替换完成后，生成x1矩阵。具体如下：

第一步：对随机数插入后生成的R矩阵的第1列进行替换操作。对于R矩阵的第1列，第1行对应的元素，分段线性混沌映射使用已知的控制变量r0，初值x0生成的随机值将R矩阵的元素进行替换，作为x1矩阵的第1列，第1行的元素。

第二步：对于矩阵R的第1列的其他元素(i,j)，分段线性混沌映射将已知的r0作为控制参数，生成的x1(i-1,1)作为初值，生成随机值将R矩阵的元素进行替换。

第三步：对于矩阵R的第1列之外的元素(i,j)，分段线性混沌映射将r1作为控制参数，x1(i,j-1)作为初值生成随机值用来替代R矩阵中的元素。具体如下：

(3)

其中，pwlcm()函数是分段线性混沌映射函数。

2.2.2 扩散操作

将替换操作后生成的x1矩阵与未进行替换前生成的R矩阵进行按位异或操作，实现像素值的改变，具体如下：

第一步：将2.2.1节生成的x1矩阵进行处理，让其值保持在[0,255]之间，以便进行按位异或操作，具体如下：

x=floor(mod(x1(i,j)×1015,256));

i=1,2,…,M;

j=1,2,…,N+1;

(4)

其中，floor()是向下取整函数，mod()是取余函数。

第二步：将x矩阵、R矩阵进行按位异或操作，生成大小为M×(N+1)的矩阵B。具体如下：

B(i,j)=B(i,j-1)⊕R(i,j)⊕x;

i=1,2,…,M;

j=2,…,N+1;

(5)

其中，⊕是按位异或操作。

2.3 加密算法

具体的加密步骤如下：

(1)原始图像P插入随机数生成矩阵R，提高了置乱和扩散的效果。如2.1节所示。

(2)分段线性混沌映射使用不同的控制参数和初值生成随机数，使用随机数将矩阵R对应的各个元素进行替换，生成矩阵x1。如2.2.1节所示。

(3)将x1矩阵以及R矩阵进行按位异或操作，生成矩阵B，实现扩散过程。如2.2.2节所示。

(4)将矩阵B以逆时针的方式旋转90度，继续进行第二轮加密过程，每一轮与上述的(1)、(2)、(3)步类似。

(5)当第四轮加密结束后，生成加密图像C，完成加密过程。

2.4 解密算法

解密算法是加密算法的逆过程，所以不再进行详细的介绍。在加密算法的每轮加密过程中，先进行随机数插入，其次进行混沌值替换，然后进行按位异或扩散，最后进行逆时针旋转90度操作。在解密算法中，要注意各个操作的顺序，以及各个操作对应的逆操作的准确性，加解密算法对于各种操作都特别敏感，存在一点错误都是无法正确解密的。

3 安全性分析

使用个人电脑对三组不同形状、不同类型的的医学图像以及一组普通图像进行加密、解密仿真实验。具体环境：win10系统，MATLAB R2020a软件。其中，本实验中使用的具体的加密密钥见表1。675×901像素的Brain医学图像的原图、加密图以及解密图如图3。256×256像素的Chest医学图像的原图、加密图以及解密图如图4。512×512像素的Tibial医学图像的原图、加密图以及解密图如图5。512×512大小的Lena图像的原图、加密图以及解密图如图6。

表1 密钥表

a) Brain原图 b) Brain密图 c) Brain解密图图3 Brain医学图像的加密、解密效果

a) Chest原图 b) Chest密图 c) Chest解密图图4 Chest医学图像的加密、解密效果

a) Tibial原图 b) Tibial密图 c) Tibial解密图图5 Tibial医学图像的加密、解密效果

b) Lena原图 b) Lena密图 c) Lena解密图图6 Lena图的加密、解密效果

通过图3～6可以看出，本加密算法不仅能对医学图像进行加密、解密，而且也能够对普通图像进行加密、解密。从实验效果可以看出，使用本加密算法不管是医学图像、还是普通图像得到的加密图是完全不同于原始图像的，丝毫看不出原始图像的任何痕迹，说明加密算法能够达到隐藏原始图像信息的目的。通过原始图像和解密图像的效果来看，从肉眼上看不出两者之间有任何区别，说明从直观上可以分析出本算法能够完全满足解密效果。

3.1 密钥空间

通常，当加密算法的密钥长度大于2100，就能够抵抗穷举攻击[18-19]。本文提出的算法中，安全性是由四轮加密保障的。每一轮加密所使用的密钥都是PWLCM混沌映射[10-11]给定的的初值和控制参数。

从密钥表中可以看出，一共有6个密钥值。每一个密钥值在计算机中都是64位，可以表示成具有15位有效数字的十进制数，所以本加密算法的密钥空间是(1015)6=1090，该密钥空间远远大于2100[20]，所以说明本算法可以有效抵抗暴力攻击，保证算法的安全性。

3.2 信息熵

信息熵是用来表征随机性的。信息熵可以作为衡量像素分布随机性的标准，信息熵的值越大，说明随机性越强[21-22]。它的数学表达式定义如下：

(6)

式中：m表示图像；H(m)表示该图像计算得出的信息熵；mi表示图像m的第i个灰度值；P(mi)表示mi出现的概率；L表示图像m的灰度级。当图像的灰度级为8时，图像的最大信息熵值为8，也就是理想的随机图像的信息熵为8[23]。

医学图像Chest的原图的信息熵和经过加密算法后得到密图的信息熵情况，另外还展示了本算法与几个最新算法的信息熵的对比情况，具体如见表2。

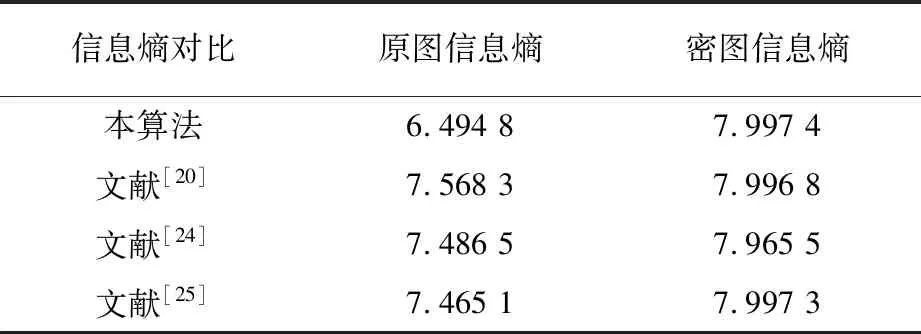
表2 原图、密图信息熵对比表

通过表2可以看出，原始图像的信息熵值与理想值8[26]相差较大，说明随机性比较低。而经过本加密算法得到的信息熵值为7.997 4，与理想值十分接近，说明经过本算法得到的加密图像随机性很强，抗攻击的能力也强，说明本加密算法的性能比较好。同时为了更加客观的说明本算法的信息熵值，对比了现有文献的信息熵值，对比结果说明本算法的信息熵值优于现有算法的信息熵值，进一步说明本算法能够达到现有算法的安全级别。

3.3 相关性

原始图像相邻像素间存在非常高的相关性，可以通过一个像素就能反映出相邻像素的信息[27]。所以对于图像加密来说最重要的是破坏相邻像素间这种强相关性，进而提高抵抗统计攻击能力。为了验证加密算法可以打破原始图像相邻像素之间的相关性，并且拥有抵抗统计攻击的能力，通过以下公式计算相关性：

(7)

(8)

(9)

式中：x和y都是图像的相邻像素值；rxy是计算得出的相邻像素点的相关性系数；E(x)是期望值；D(x)是方差。加密算法应该有效减低图像相关性，理想情况下，加密图的相关性为0[28]。本实验对Chest医学图像的原图、加密图、解密图分别随机选取1000对相邻像素进行相关系系数计算，另外与最新算法的相关性系数进行对比，具体情况见表3。

从表3可以看出，原图的三个方向的相关系系数都较大，说明相关性特性明显，被统计性攻击破解的风险极大。经过加密后得到的加密图的三个方向的相关系系数接近于0，也就是说明加密图的像素值之间几乎不存在关系。本算法与最新算法的相关性比较，通过数值看出相关性基本上低于最新算法的相关性。因此，可以看出本加密算法降低图像相关性的能力较强。

表3 原图、密图相关性系数对比表

另外，本实验还通过观察图像的相关性散点图的方式展示相关性情况。其中，Chest原图的水平、垂直、对角线方向的相关性情况如图7。 Chest加密图的水平、垂直、对角线方向的相关性情况如图8。

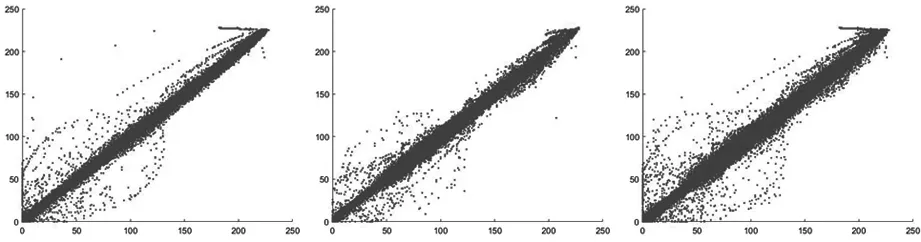
a) 原图水平 b) 原图垂直 c) 原图对角线图7 原图相关性散点图

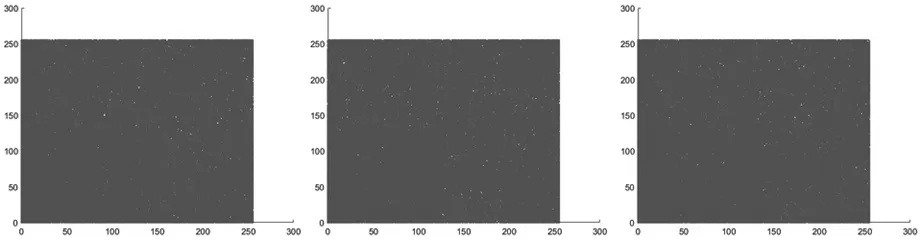
a) 密图水平 b) 密图垂直 c) 密图对角线图8 密图相关性散点图

通过原图和密图的相关性散点图可以看出，原图的大多数相邻像素对集中分布在对角线或者对角线两侧的范围内，而经过本算法加密后的相邻像素对能够均匀、随机地分布在整个坐标系的范围内，说明本加密算法能够有效打破明文像素间的强相关性，并且能够有效的抵抗统计攻击。

3.4 直方图

一般像素的直方图可以反映出像素值的分布情况[9,30]，攻击者通过对像素值进行分析即可破解图像。本小节得到的测试图像加、解密的灰度直方图如图 9。中直方图的横坐标用来表示其灰度值，纵坐标用来表示像素的个数。

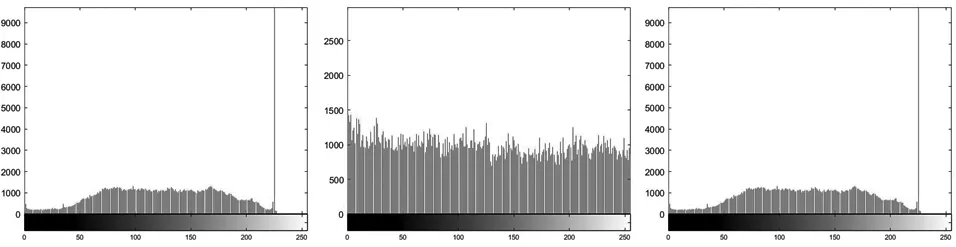
a) 原图直方图 b) 密图直方图 c) 解密图直方图图9 原图、密图、解密图的直方图分布

从图9可以看出，原图像素灰度值出现的概率非常不均匀，最多的出现次数高达9 000多次，而最少的几乎为0,这就说明图像的安全性非常弱，是很容易被攻击者分析出图像特点的。而经过本算法加密后得到的加密图像直方图变得非常均匀，从而可以有效的防止出现原始图像信息的泄露，进而有效的抵抗统计攻击。

3.5 鲁棒性分析

本算法对医学图像进行加密，除了需要保证加密效果良好，还需要有一定的鲁棒性。鲁棒性包括抵抗噪声攻击的能力，裁剪攻击的能力等[25,31]。本实验以先对加密图进行一定程度的椒盐噪声干扰，然后再进行解密的方式，分析本算法抵抗噪声攻击的能力。对Chest加密图像分别进行0.000 5、0.005以及0.05的椒盐噪声干扰，然后进行解密过程得到解密图像，具体如图10。

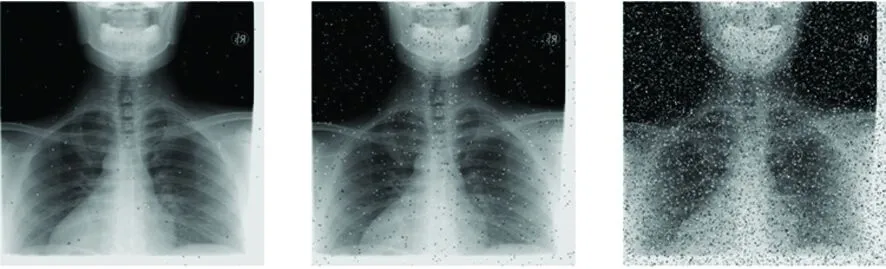
a) 0.000 5噪声 b) 0.005噪声 c) 0.05噪声图10 不同程度椒盐噪声后生成的解密图

从图10可以看出，经过不同程度的椒盐噪声污染后生成的解密图虽然清晰度受到了一定程度的干扰，但是仍然看出图像的有效信息，说明本算法抵抗噪声攻击能力较强，具有一定的鲁棒性。

4 结 语

本文提出了一种基于分段线性混沌映射的医学图像加密算法。该算法采用四轮加密的方式，确保加密算法的有效性和安全性。每一轮加密中，首先原始图像进行随机数插入，其次使用分段线性混沌映射进行像素值的替换，然后对生成矩阵以及替换前的矩阵进行按位异或操作，改变像素值的大小，最后将矩阵逆时针旋转进行下一轮加密，持续进行四轮加密，得到加密图像。从仿真实验和安全性分析结果可以看出，该算法不仅可以对医学图像进行加密而且可以对普通图像进行加密，与目前算法相比安全性能更高，并且具有一定的鲁棒性，适合用于医学图像加密。