基于博弈组合赋权-TOPSIS法的富水软岩山岭隧道塌方风险评价
吴波, 周路, 刘聪
(东华理工大学土木与建筑工程学院, 南昌 330013)
隧道的建设可以使得交通更加便利,尤其是在中国东南多丘陵的地区,据统计,中国修建山岭隧道的数量远多于水下隧道和城市道路隧道,在山区发展过程中,公路隧道的建设呈现出规模大、埋深大、隧道宽长等显著特点[1]。公路山岭隧道因存在隐蔽性以及地质条件复杂性和周围环境恶劣性,导致施工过程中的风险性大大增加。为了保证施工的安全性和顺利完成施工建设目标,进行隧道工程施工安全风险性评价便显得尤为重要。
20世纪90年代初,随着风险评估理念在隧道工程领域被提出后,中外学者针对隧道开挖过程中可能会发生的安全风险问题开展了大量研究。卢庆钊[2]通过结合层次分析法和模糊数学理论提出了针对隧道开挖穿越富水层的隧道突水安全风险评估模型,并通过实例验证了该分析方法的可靠性。孙浩等[3]基于可拓学理论构建了富水隧道评价指标体系,运用层次分析法(analytic hierarchy process,AHP)法计算指标权重,引入集对分析原理确定隶属度函数,最后计算得到隧道安全风险等级,由隧道实例进行对比,验证了该模型的适用性。刘灿等[4]通过结合熵权法和改进的灰色关联理论构建了一套针对公路隧道塌方的风险评价模型,并与工程实例进行印证,检验了该模型的科学性。针对软岩隧道在开挖过程中容易产生大变形的问题,何乐平等[5]提出了一种基于云模型并结合博弈论优化序关系法(G1)和CRITIC(criteria importance though intercrieria correlation)法所求权重值的综合风险评价方法,并在工程实践中进行了验证。王婧等[6]通过运用博弈论将群组G2法和CRITIC法分别求得的主客观权重进行综合,并结合可变模糊评价法构建了一种针对岩山隧道塌方的风险评价模型。针对指标权重的评价过度依赖专家经验而导致评价结果准确度低的问题,陈舞等[7]基于对粗糙集理论的改进,通过引入信息熵理论确定权重值,并结合模糊综合评价法提出了一种简化风险因素的评价模型,并加以验证。张延杰等[8]在对山岭隧道进行风险评价过程中用定性、定量的尺度将评价指标加以区分,并通过结合功效系数法和多级加权迭代法提出了一种静态和动态的风险评估模型。吴波等[9]通过将隧道风险因素进行多层次的剖析并通过应用熵值理论计算出指标权重值,最后引入多级模糊评价理论对风险目标进行评价。
综上所述,目前针对隧道施工过程中塌方的风险研究已经有了一定的成果,但也还存在有待深入探讨的问题,如在确定评估指标权重时进行主、客观赋权的合理性、所构建评价模型的适用性等。富水软岩山岭隧道所处区环境恶劣,风险因素具有不确定性和模糊性,评价过程中各风险因素间存在关联性和冲突性。针对上述问题引入D数理论对AHP法进行改进,以解决在不确定性环境中指标权重集的计算;采用CRITIC法确定客观权重,以考虑指标间的相关性和差异性;通过博弈论对所求权重值进行组合优化得到综合权重,然后对初始矩阵进行加权规范化后运用逼近理想解排序法(technique for order preference by similarity to an ideal solution,TOPSIS)进行风险等级评定,最后,通过隧道实例验证所提模型的适用性,为富水软岩隧道塌方风险评估提供了一种适用的方法,也为今后类似工程提供了一个案例参考。
1 构建评价指标体系和等级划分标准
1.1 风险评估因素识别
富水软岩山岭隧道地质环境复杂,施工中存在较多的风险因子,为选取更加合理有代表性的评价指标,通过在查阅文献[10-15]的基础上结合工程实际情况和工程概况资料,建立包括工程地质、勘查设计、组织管理和环境气候在内的4个一级指标,16个二级评估指标的富水软岩山岭隧道塌方评价指标体系,如图1所示。
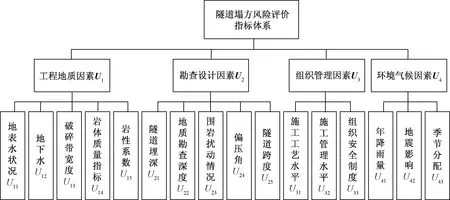
图1 隧道塌方评价指标体系
1.2 隧道风险评价等级划分标准
为了全面综合地对富水软岩山岭隧道风险情况进行分析,在文献[7-9,11,14-15]研究成果基础上,得到各指标等级标准,如表1所示。
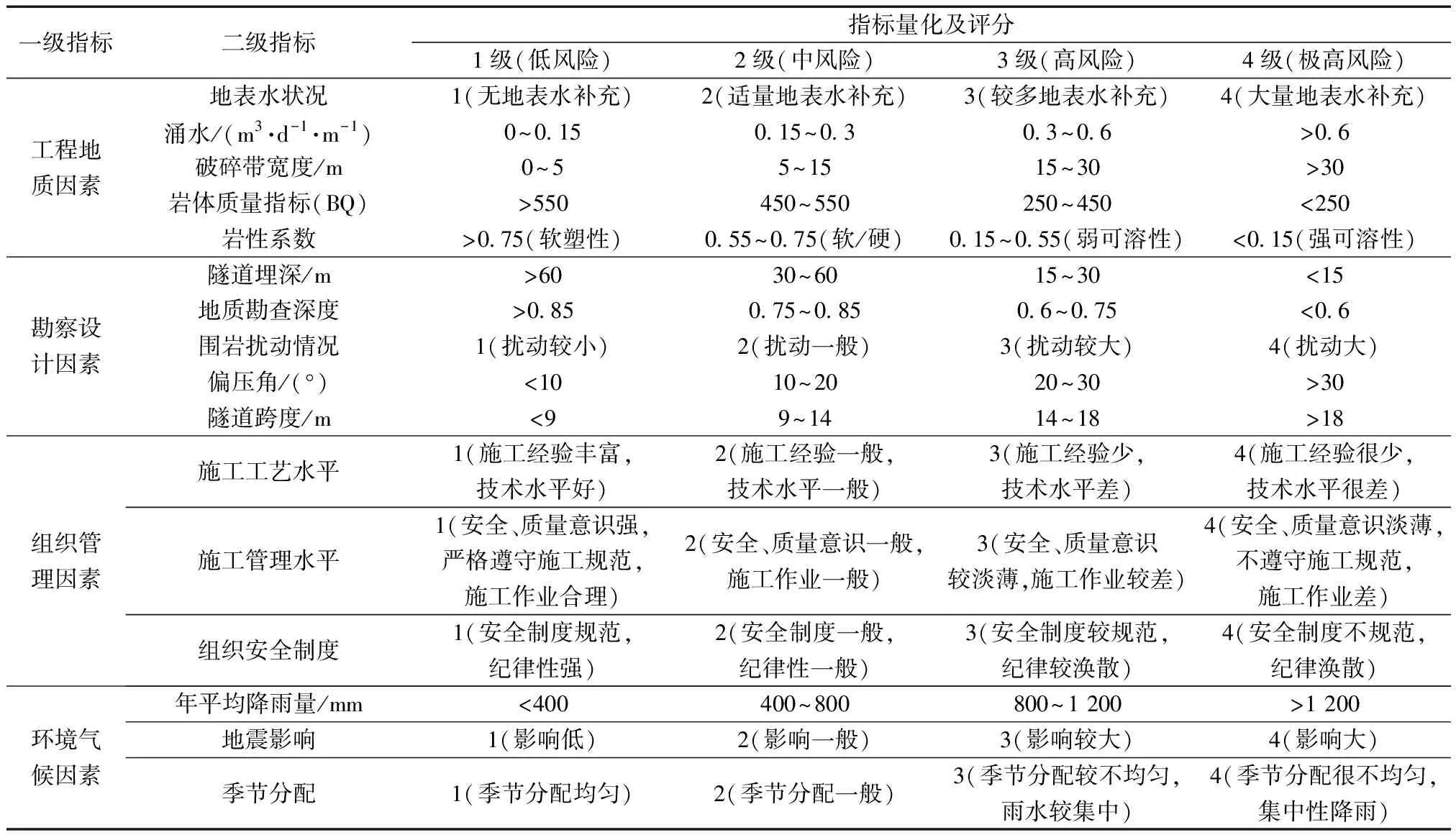
表1 隧道塌方评价指标分级标准
2 理论分析
2.1 博弈论组合赋权法
评估指标权重值的精确性和合理性对评价结果至关重要,能够影响待评价目标最终的风险等级,在充分发挥专家主观能动性的基础上兼顾工程实际情况,通过运用D数层次分析法(D-number analytic hierarchy process,D-AHP)和CRITIC法分别确定主、客观权重值,然后引入博弈理论进行权重组合优化,最后根据所求综合权重进行加权并运用TOPSIS法进行隧道塌方风险评价。
2.1.1 基于D数理论改进AHP的主观赋权
D数理论。D数理论是在D-S证据理论(D-S evidence theory)基础上进行的理论创新和延申,处理不确定和不完整信息的能力更强,应用范围也更大,因此,将D数理论引入对山岭隧道塌方风险评价中。
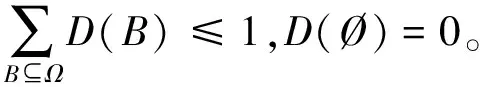
(1)
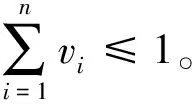
定义2假设有待评估样本G={G1,G2,…,Gn},且有构成的矩阵R,以G×G的方式存在,则有相关性质:μR:G×G→[0,1],其中μR为矩阵R的模糊偏好关系。矩阵R=[rij]n×n可表示为
(2)
式(2)中:rij为专家Gi相较于专家Gj的偏好程度,i=1,2,…,n;j=1,2,…,n。
(3)
定义3设有一个评估集合G={G1,G2,…,Gn},其中存在的D数偏好关系为:RD:G×G→D,矩阵形式可表示为
(4)
RD矩阵满足条件为
(5)
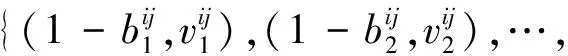
(6)
(7)
Dii∈{(0.5,1.0)}, ∀i∈{1,2,…,n}
(8)
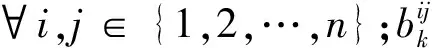
D-AHP法。经D数理论改进的层次分析法具有将每位专家给出的评估信息融合为群评估的能力,在不确定性的评估环境中能够很好地发挥其优势[16]。
D-AHP法的使用步骤如下。
步骤1由专家进行成对比较,构建偏好关系矩阵RD,经融合后得到实数矩阵RC。
步骤2计算偏好概率矩阵有RP。
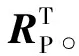
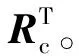
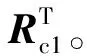
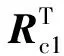
不一致性系数检验可表示为
(9)
2.1.2 基于CRITIC法的客观赋权
由于熵权法等客观赋值法处理指标间相关性能力较弱,故引入CRITIC法,该方法能充分考虑评估指标内部存在的相互关联和指标间的冲突,提高评价值的科学性。主要步骤如下。
步骤1假设有m个方案和n个评价指标,可建立指标矩阵。
(10)
式(10)中:xij为第i个方案的第j个指标取值。
步骤2对第i个方案的第j个指标进行无量纲化,得到效益型指标为
(11)
式(11)中:maxj(xij)为第i行方案中的最大指标值j;minj(xij)为第i行方案中的最小指标值j。
得到成本型指标为
(12)
步骤3计算相关系数,其计算公式为
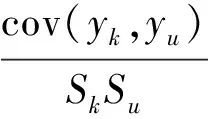
k=1,2,…,m;u=1,2,…,n
(13)
式(13)中:cov(yk,yu)为第k个指标和第u个指标的协方差;yk为m个方案中的第k个指标值;yu为n个评价指标中的第u个指标值;Sk和Su分别为第k个指标和第u个指标的标准差。
标准差计算公式为
(14)
步骤4计算信息量,计算公式为
(15)
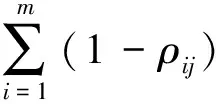
步骤5确定客观权重,其计算公式为
(16)
2.1.3 基于博弈论综合权重的计算
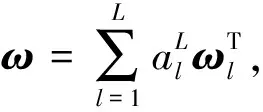
(17)
根据微分性质,其所对应的线性方程标准化处理后可得
(18)
综合权重向量为
(19)
2.2 TOPSIS法计算步骤
TOPSIS法是一种科学性的多目标决策分析方法,被广泛应用于多种工程领域中[17-19],其计算步骤如下。
步骤1构建初始决策矩阵。
(20)
式(20)中:aij为第m个方案的第n个评价指标(i=1,2,3,…,m;j=1,2,3,…,n)。
步骤2对原始数据进行无量纲化后通过式(21)进行加权,得到加权标准化决策矩阵C为
C=WB=(ωjbij)m×n
(21)
式(21)中:W为综合权重;B为标准化决策矩阵。
步骤3计算正、负理想解,计算公式分别为
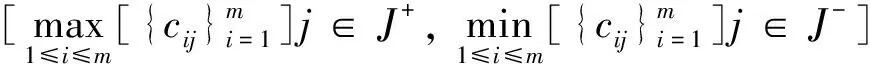
(22)
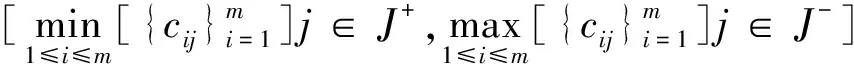
(23)
式中:J+、J-分别为效益性集中最大值和成本性集中最小值。
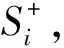
(24)
(25)
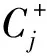
步骤5确定相对贴近度Gi,其表达式为
(26)
式(26)中:Gi∈[0,1],Gi值越接近1则表示贴进度越接近正理想解。
3 工程实例
3.1 工程概况
以黄砂富水隧道为工程依托,隧道位于丘陵区,为单线双向两车道,起止里程为LZK0+855~LZK2+105,全长1 250 m,最大埋深161 m,进出口均设计为端墙式洞门。根据地质详勘报告可知隧道进口仰坡体主要由残积层与全、强风化层构成,工程性质较差,仰坡不稳定;出口仰坡体主要由砂质黏性土和全、强风化层构成,岩体完整性较差;在隧道范围内地表水主要是山间冲沟水,隧道右侧冲沟发育,沟面较窄,雨季降水集中流量较大;地下水位勘测分析位于设计线之上。隧道进出口均存在偏压、涌水,施工中易产生塌方、突水、突泥等现象。
3.2 样本段隧道风险评价
3.2.1 样本段隧道评价指标值
选取5段有代表性的隧道洞身进行研究,结合项目概况、地质地形图和现场实测数据等资料,获得评价指标如表2所示。

表2 各样本段区评价指标值
3.2.2 基于D-AHP法的主观权重
(1)一级指标权重计算。邀请施工现场专家综合考虑所选取样本段隧道情况,对评价指标进行打分,取一级指标评估打分为例,得到D数矩阵RD为

(27)
根据D数理论的融合公式,得到实数矩阵RC为
(28)
(29)
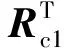
(30)
因为专家可信度较高,则取λ=3,解方程组得:ω1=0.404,ω2=0.314,ω3=0.208,ω4=0.074。
(2)二级指标权重计算。二级评价指标的权重及其综合权重,如表3所示。
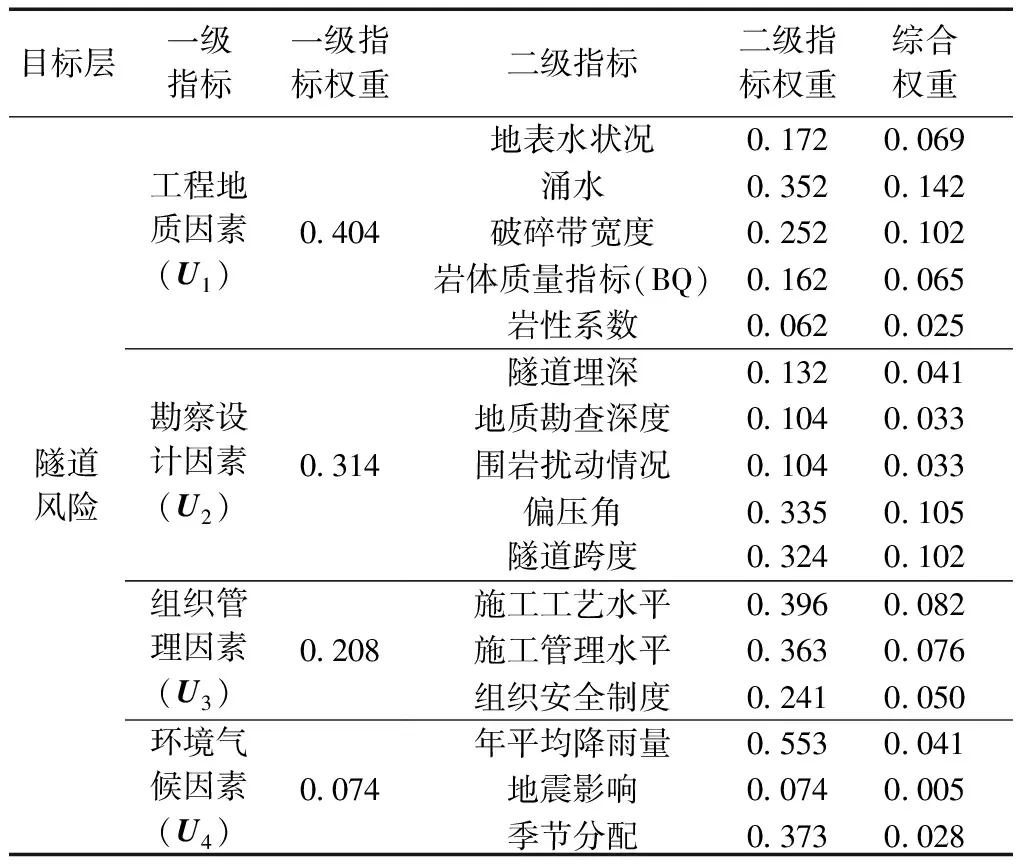
表3 评价指标权重系数
3.2.3 基于CRITIC法的客观权重
根据式(11)、式(12)及表2中的样本原始数据可得规范化矩阵P为

由式(13)~式(16)可得客观权重为τ=(0.099,0.156,0.050,0.043,0.041,0.061,0.052,0.041,0.046,0.046,0.063,0.062,0.057,0.048,0.059,0.077)。
3.2.4 基于博弈论组合赋权
根据式(17)~式(19)将上述所求主客观权重进行组合优化后得到综合权重ω*=(0.078,0.146,0.086,0.059,0.030,0.047,0.038,0.035,0.087,0.085,0.076,0.071,0.052,0.043,0.022,0.042)。
3.2.5 博弈组合赋权-TOPSIS法风险评价模型
根据式(20)、式(21)对表2中的实测数据进行无量纲化并加权标准化得
由式(22)、式(23)得到正负理想解标准化得:C+=(0.078,0.146,0.086,0.059,0.030,0.047,0.038,0.035,0.087,0.085,0.076,0.071,0.052,0.043,0.022,0.042),C-=(0,0,0,0,0,0,0,0,0,0,0,0)。
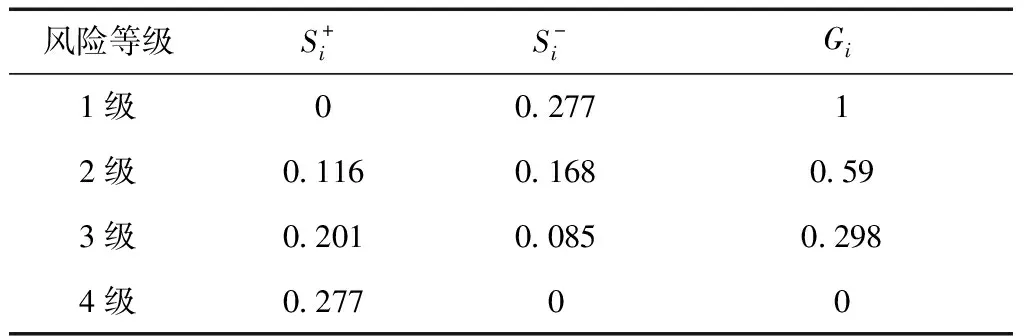
表4 隧道塌方风险等级评价结果
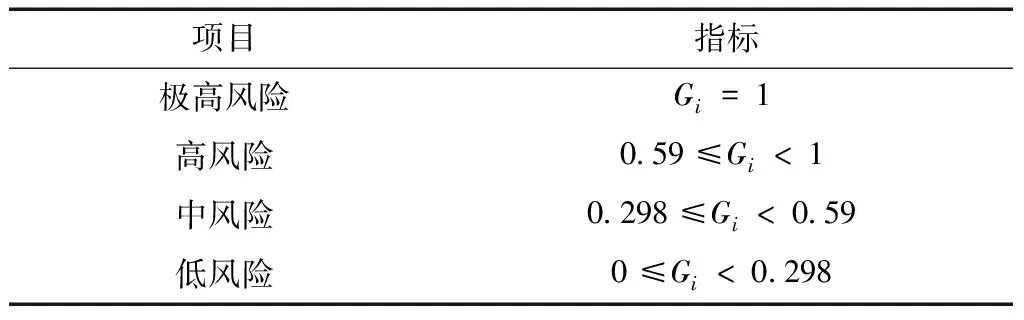
表5 隧道塌方风险等级
3.2.6 隧道样本段风险评价
将表2中5个样本段的实测数据进行无量纲化,并由式(21)计算得到加权决策化矩阵为

根据式(22)、式(23)计算得到C+=(0.078,0.146,0.086,0.059,0.030,0.047,0.038,0.035,0.087,0.085,0.076,0.071,0.052,0.043,0.022,0.042),C-=(0,0,0,0,0,0,0,0,0,0,0,0)。评价结果如表6所示。
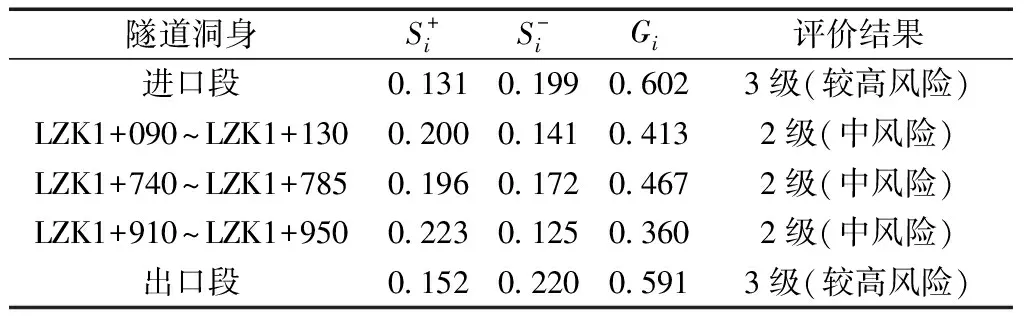
表6 各样本段隧道塌方风险评价结果
由表6可知,5个样本段隧道中进出口段风险等级为3级,即较高风险,而洞身段隧道风险等级为2级,即中风险。由表3可知,根据专家经验在富水软岩隧道塌方风险评价中,涌水量、偏压角等风险因素占有较大比例,并再经过博弈综合主客观权重后也具有显著的占比,其中涌水量占有最大的0.146,而通过结合项目实际情况也可知道隧道的进出口段岩体较不完整,仰坡稳定性较差,存在地形偏压和明显的涌水情况,隧道施工风险较大,其评价结果和实际情况相吻合;而隧道洞身LZK1+090~LZK1+130、LZK1+740~LZK1+785、LZK1+910~LZK1+950段主要为中风化岩层,洞身大部分段落位于地下水水位之下,富水性较进出口段更弱,地质情况也较为简单,风险相比较于进出口段更低,因此可判断风险评价结果可信。
4 结论
(1)通过参考项目资料,并在借鉴相关文献研究的基础上针对富水软岩山岭隧道的特点,建立了包括工程地质因素、勘察设计因素、组织管理因素和环境气候因素在内的4个一级主、客观风险评价指标体系,并细分为16个具有代表性、可行性和可操作性的二级风险评价指标体系。
(2)基于传统层次分析法在分析评价对象时处理不确定性信息能力较弱的情况下,引入D数理论进行改进,可以充分体现出评价指标两两比较时的模糊关系,更加合理的进行主观赋权;基于所构建评价指标间参数的关联性和冲突性,选用CRITIC法便于量化指标间的关系然后进行客观赋权,通过将实际测量到的客观数据进行直接导入提高了赋权的科学性,其特点尤其在文中计算地表水状况和涌水量等因素时有较明显的展现;最后,运用博弈理论组合优化后得到的综合权重值进行加权,并通过TOPSIS法进行风险等级判定。
(3)通过构建组合赋权-TOPSIS法风险评价模型,并结合选取的5个富水软岩样本段隧道实例进行分析计算,最终得到隧道塌方风险等级在中风险和高风险之间,经过分析可知评价结果和工程实际情况一致,验证了该模型在针对富水软岩隧道的风险评价中具有一定的准确性和适用性,可在今后类似的隧道工程中推广及应用。

