基于SMP准则的冻融受荷岩石损伤软化模型
史磊,侯克鹏*,孙华芬
(1.昆明理工大学国土资源工程学院,昆明 650093;2.云南省中-德蓝色矿山与特殊地下空间开发利用重点实验室,昆明 650093)
高寒地区拥有丰富的矿产资源[1],但其工程中的岩石常年受到冷热交替、围压等作用的共同影响,因此研究冻融受荷岩石的损伤软化模型具有重要的意义。
运用损伤理论研究冻融岩石的本构关系一直是寒区岩土工程研究的热点领域。慕娜娜[2]运用损伤力学理论及Drucker-Prager(D-P)准则,基于电子计算机断层扫描(CT)分形维数建立了冻融-荷载作用下考虑残余强度的岩石损伤本构关系。许梦飞等[3]基于广义Hoek-Brown(H-B)及连续损伤理论,并运用完全隐式求解算法,解决该模型数值求解中奇异点的问题,结果表明,所建模型可以较好的应用于冻融边坡工程。宋彦琦等[4]通过探究冻融岩石的损伤特性,建立了灰岩的衰减模型。郎东明等[5]基于损伤等效原理与Weibull分布理论,分析了冻融作用下岩石的能量演化机制及损伤变化规律。陈国庆等[6]根据塑性条件引入时效损伤因子,建立了分数阶损伤蠕变模型。夏飞等[7]通过对岩石孔隙度及相对强度随冻融次数的变化进行指数拟合,建立了拉压强度的冻融岩石劣化模型。折海成等[8]建立了以体积膨胀率为考察变量来表征黄土的统计损伤模型。孟凡东等[9]的研究表明,冻融砂岩劣化模型满足指数函数关系。戚利荣等[10]对花岗岩进行宏微观多尺度综合研究发现冻融及荷载耦合作用下的总损伤因子都随冻融循环次数呈增长趋势。刘杰等[11]基于孔隙率,弹性模量等与冻融次数的变化规律,建立了层进式损伤弹性模量劣化预测公式。
综上所述,岩石损伤模型的构建主要运用:H-B准则、D-P准则等对岩石的损伤加以量化。近年来,众多学者开始运用SMP(spatial mobilized plane)和Lade准则研究岩石的损伤问题。但是基于SMP准则研究冻融受荷岩石的损伤本构关系的报道较少。为此,在冻融-荷载耦合条件下,根据应变等价性理论,采用双参数的Weibull统计损伤分布描述岩石微元破坏,考虑岩石残余强度的影响,结合SMP强度破坏准则,建立考虑中间主应力的冻融受荷岩石统计损伤软化模型。通过引用他人模型及相关试验数据进行对比验证分析,其拟合效果较为合理,为深入分析冻融-荷载耦合作用下的损伤本构关系提供参考。
1 岩石损伤演化方程的建立
根据谌彪[12]对冻融损伤因子的分析可知,冻融循环作用于岩石内部的空隙、微裂隙等缺陷,导致岩石内部微观结构的力学性质发生持续性改变,而弹性模量是岩石的重要力学参数,不但能够反映岩石受外力时抵制变形的强度,而且能够表征岩石内部颗粒间相互作用。冻融损伤变量的表达式为
(1)
式(2)中:Dn为冻融损伤因子;En为冻融n次后的弹性模量;E0为未损伤岩石的弹性模量。
寒区岩石不仅经受冻融循环的影响同时还受外部载荷的作用,考虑二者耦合作用是十分必要的。因此,运用双参数Weibull分布函数对岩石内部损伤进行表征,其表达式为
(2)
式(2)中:F为微元强度统计分布变量;m、F0为统计分布参数,与岩石材料力学性质相关。
岩石微元损伤是通过概率密度进行度量,岩石材料微元的持续损伤,最终导致宏观力学性能劣化。对式(2)进行积分可得到微元体破坏的损伤变量表达式为
(3)
冻融受荷岩石总损伤效应可以等效为冻融和受荷两种损伤状态的耦合,两者以不同的力学机制使岩石内聚力不断减弱,其总损伤效应可根据文献[13]中推导得出,其表达式为
Dm=D+Dn+DDn
(4)
式(4)中:Dm为冻融受荷总损伤变量;DDn为冻融受荷的耦合项。
将式(1)、式(3)代入式(4)可得
(5)
2 基于SMP准则的岩石损伤软化模型建立
2.1 SMP强度准则
SMP准则表达式为
(6)
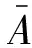
(7)
式(7)中:σ1、σ2、σ3分别为最大、中间和最小主应力。
为使得SMP准则具有更好的适用性,Mastuoka等[14]对其进行如下修正,引入黏结应力σ0,其表达式为
σ0=ccotφ
(8)
式(8)中:c为黏聚力。
则修改后的SMP强度准则为
(9)
式(9)中:
(10)
根据相关流动法则,得到黏性材料的SMP强度准则的表达式为
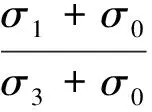
(11)
2.2 基于残余强度的岩石统计损伤演化模型
岩石未损伤部分服从广义虎克定律,其表达式为
(12)
根据张全胜等[15]推广的应变等价原理,以及张慧梅等[16]对冻融受荷岩石微元损伤的分析,岩石在冻融荷载作用下,岩石受荷损伤状态下的有效应力作用于冻融损伤引起的应变与冻融损伤对受荷损伤引起的应变等价。结合苏艳军[17]提出的冻融受荷作用下材料产生各向同性的损伤,损伤仅在最大主应力方向产生假设,因此,对已有的冻融荷载耦合作用下损伤模型提出的假设进行描述,如图1所示,假设名义应力σi的作用面积为A,有效应力的作用面积为A1,残余强度σr的作用面积分别为损伤面积A2及破坏面积A3。
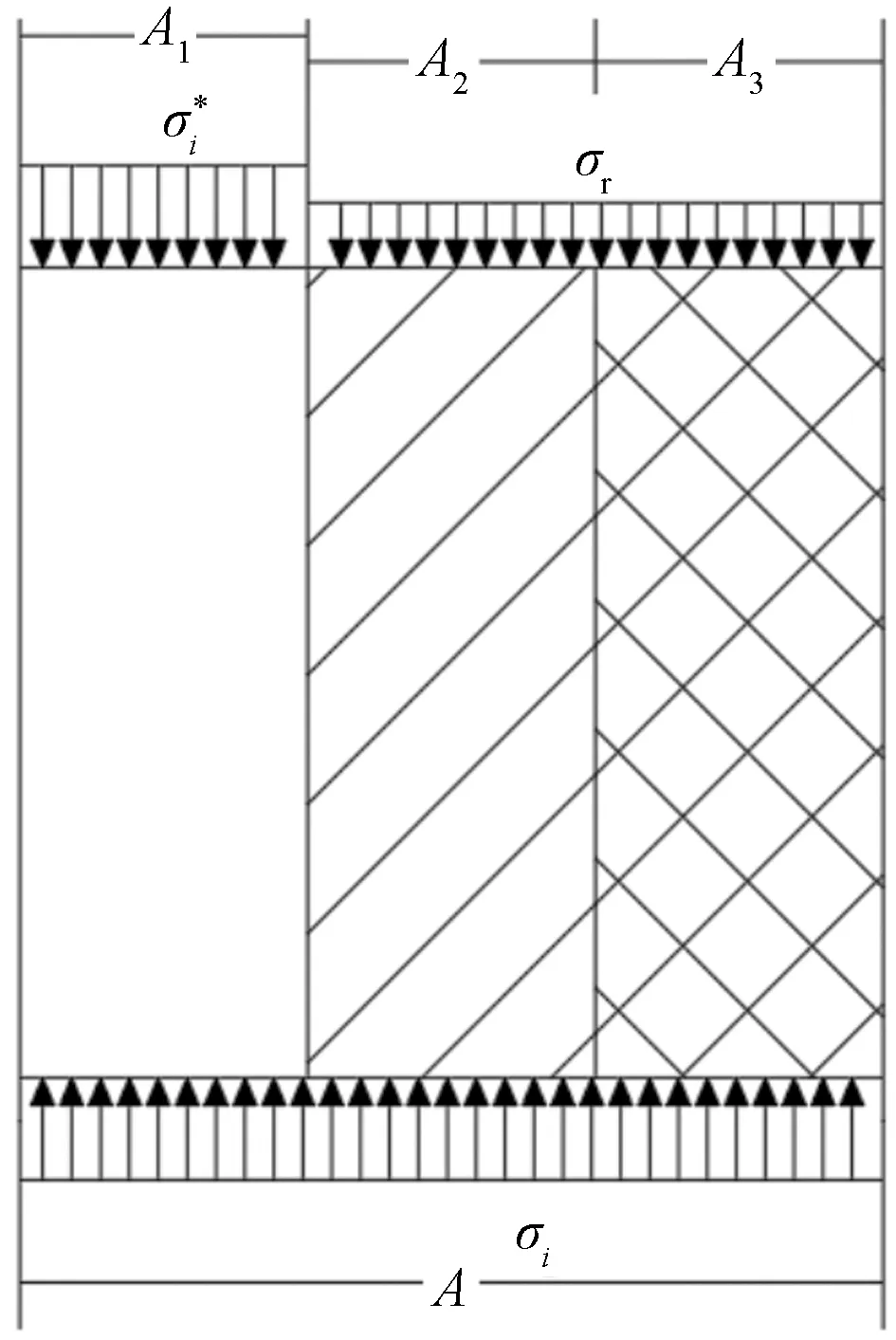
图1 岩石单元微观受力分析
由上述假设可得
(13)
式(13)中:
A=A1+A2+A3
(14)
定义损伤变量为
(15)
联立式(13)~式(15)可得
(16)
根据岩石变形协调关系可得
(17)
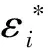
根据上述假设,侧向荷载全部由岩石未损伤部分承担,可得
(18)
联立式(5)、式(16)~式(18)可得
σ1=(Enε1+2μnσ3)(1-Dm)+σrDm
(19)
式(19)中:μn为冻融n次后的泊松比。
假设岩石的微元体破坏服从SMP准则,依据式(11)得到F的表达式为
(20)
由式(5)、式(19)、式(20)得到考虑残余强度的冻融-荷载作用下基于SMP准则的岩石损伤本构关系式为
(21)
式(21)中:
(22)
根据SMP强度准则表达式,对冻融受荷岩石的损伤演化过程进行修正,其表达式为
(23)
2.3 基于SMP冻融受荷岩石损伤软化模型
联立式(21)、式(23)得出冻融-荷载下岩石损伤软化模型,可表示为
(24)
3 岩石损伤本构模型及参数确定
3.1 参数m、F0确定
模型参数的确定对岩石的非线特性起至关重要作用,因此,可利用峰值点偏导数法进行确定,其峰值条件为[18]
(25)
因此将式(22)、式(23)代入式(21)对应变求偏微分得
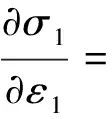
(26)
将式(26)变形可得
(27)
变形式(21),可得
(28)
根据峰值条件,由式(25)、式(26)及双参数的Weibull统计分布函数的定义可得
(29)
(30)
式中:Fc为峰值点对应的F值;σc为峰值应力;εc为峰值应力对应的应变。
3.2 参数σ0确定
从式(8)给出的黏结应力σ0的表达式可知,利用c、φ值通过式(31)、式(32)获取[19]。
(31)
(32)
式中:σp为最优关系曲线在纵轴上的截距;P1为斜率。
4 基于SMP准则的冻融受荷岩石损伤软化模型验证
为了验证基于SMP准则的冻融受荷岩石损伤化方程的合理性,引用文献[16]中高孔隙率红砂岩不同冻融循环次数及围压下的应力-应变曲线峰值点与模型理论曲线1的峰值点进行对比,如表1[16]所示。
由表1岩石的峰值点对比结果可知,根据式(24)计算得到不同冻融循环次数及围压下岩石的峰值强度与试验结果拟合度较高。由于文章篇幅有限,仅对文献[16]中围压为5 MPa,冻融循环5次的三轴抗压试验数据及文献[20]中低孔隙率花岗岩在围压为10 MPa,冻融循环次数为50次的三轴抗压试验数据进行验证,并对文献[16]所建的理论曲线及文献[21]建立的理论曲线2与式(24)计算的理论曲线1行对比验证分析,如图2所示,试验所得力学特性参数如表2[16,20]所示。

表1 不同冻融循环次数及围压下试验曲线和理论曲线的峰值点对比[16]

表2 各值计算结果[16,20]
由图2可知,基于SMP破坏准则构建的损伤模型理论曲线与文献[16]和文献[21]所建的理论模型,在峰值应力前均能较好的反映冻融受荷岩石变形特征,并与试验曲线可以较好的吻合,但是,从岩石应力-应变峰值后曲线可以看出,本文模型对于冻融受荷岩石峰后软化特征更符合岩石损伤变形规律,而张慧梅所建模型对于岩石残余强度下降特征不能较好的反映,并且文献[21]所建模型在峰值强度后应力跌落速率较快,与试验数据中的冻融受荷岩石变形规律不符,以上现象进一步表明本文模型的合理性,也证明本文模型不仅适用于高孔隙率,强度较低的红砂岩,也适用于低孔隙率,强度较高的花岗岩,从而验证了本文模型对所试验的岩石,具有较好的实用性。
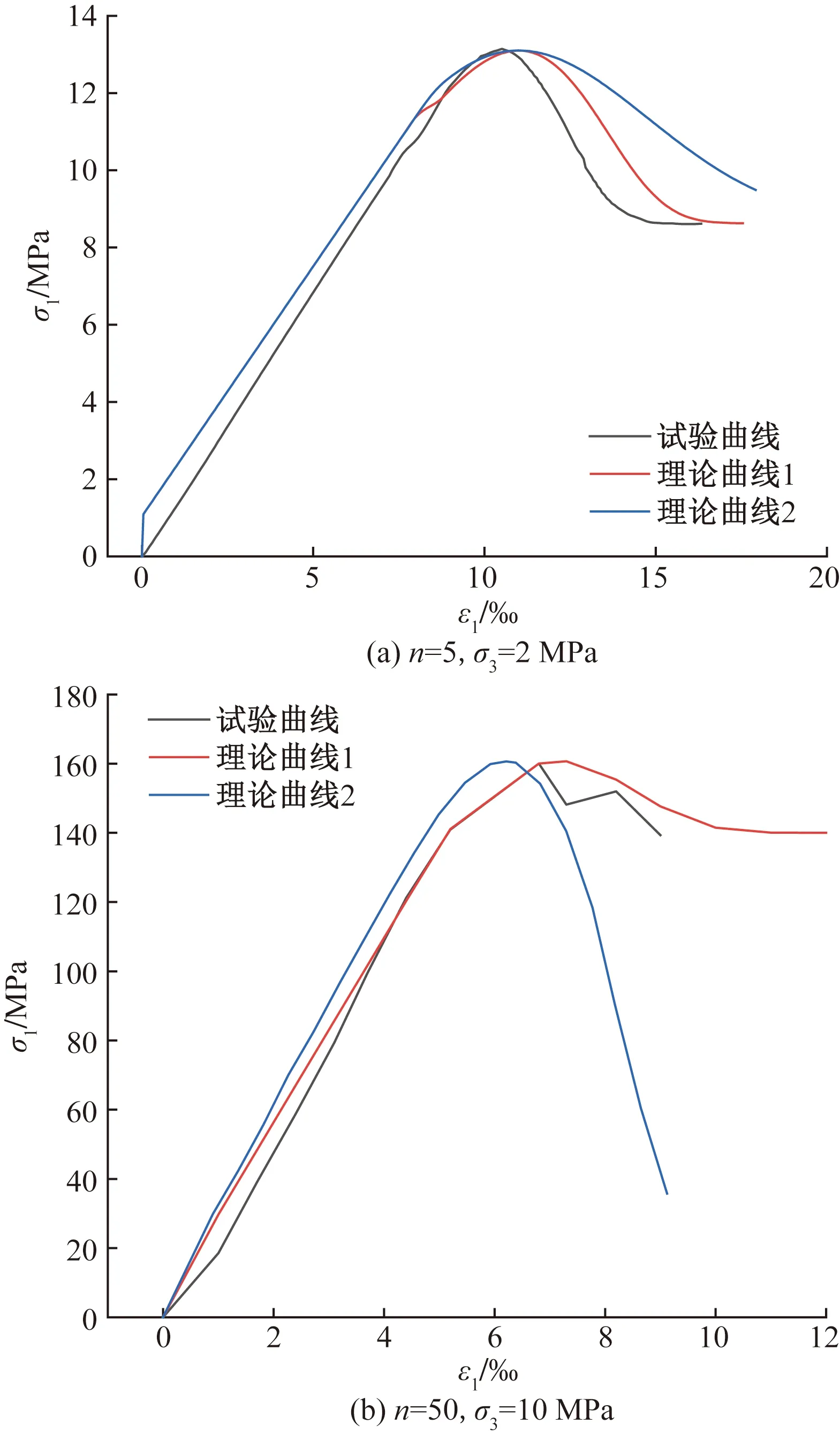
图2 岩石本构模型理论与试验曲线对比
5 冻融-荷载作用下岩石损伤力学特性分析
5.1 不同冻融次数及围压下损伤变量演化
利用文献[18]的相关试验数据,根据式(4)对不同冻融循环次数及围压下总损伤变量Dm进行演化,如图3所示。可以看出,总损伤变量Dm演化曲线呈现“S”形,岩石受冻融-荷载损伤变形初期,随着冻融次数及围压的增大,岩石损伤变形曲线水平阶段不断增大延长,随后曲线发生凹陷,产生塑性变形,且凹陷角度逐渐增大;随着外部荷载的不断增加,加重岩石的内部损伤发生塑性屈服,且冻融及围压增大时,塑性屈服阶段的斜率逐渐减小;最终岩石强度急剧降低丧失变形能力发生软化,峰值后残余变形发生,宏观上岩石出现明显的破裂面发生完全破坏,此时损伤为1,不再产生变化。
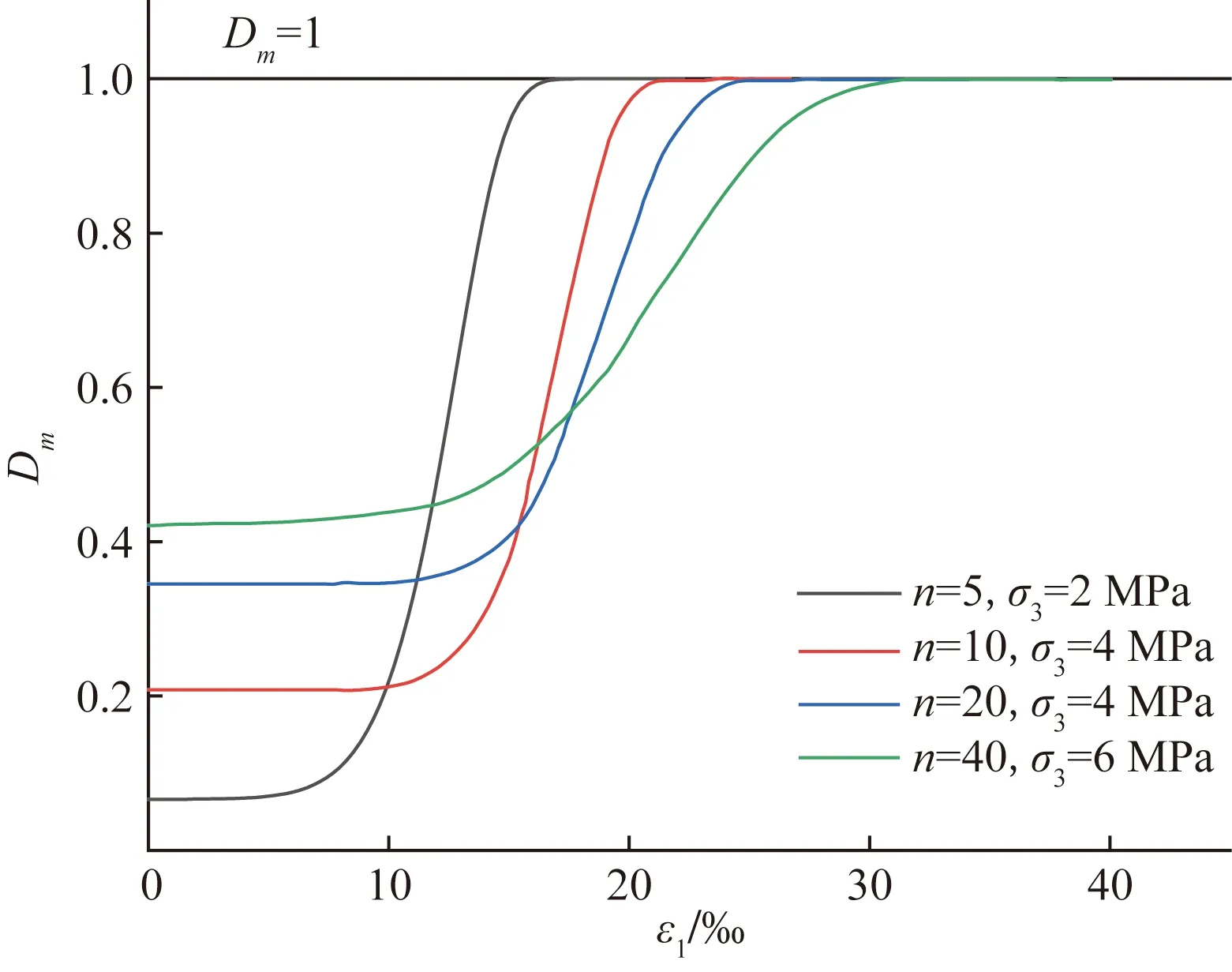
n为冻融次数
5.2 参数m和F0对应力-应变曲线的影响
为了反映模型参数对冻融受荷岩石整个变形过程中的特征意义及影响,以文献[18]中冻融循环次数为5次,围压为2 MPa的红砂岩为例,根据岩石应力-应变曲线的变化情况,对参数m和F0的值进行分析,如图4、图5所示。
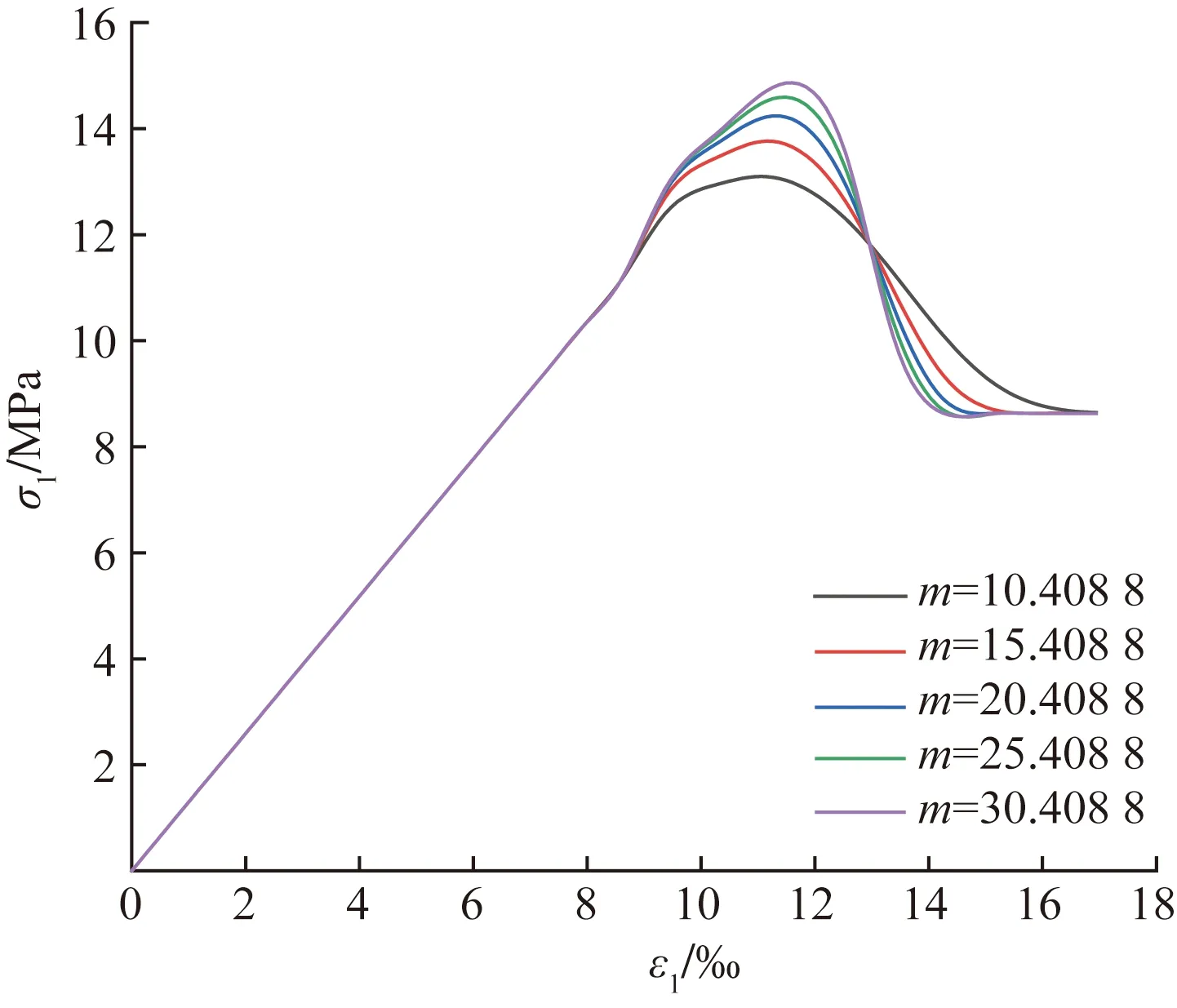
图4 参数m对应力-应变曲线的影响
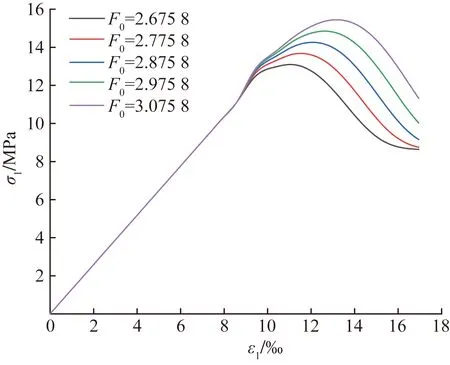
图5 参数F0对应力-应变曲线的影响
由图4可知,控制F0不变,m的增大的情况下,冻融受荷岩石的峰值强度明显增高,伴随着峰后应力跌落速率也随之加快。由图5可知,控制m不变,F0的增加的情况下,冻融受荷岩石的峰值点增高且向右偏移,说明岩石达到峰值强度时所需的应变量也相应增大。
5.3 参数m和F0对总损伤演化曲线的影响
为了解Weibull统计损伤分布中双参数对岩石总损伤量的影响程度,由式(5)可计算得到冻融受荷岩石的总损伤量,通过适当变动参数m和F0,分析不同参数m和F0的值对冻融受荷岩石总损伤量的影响,如图6、图7所示。
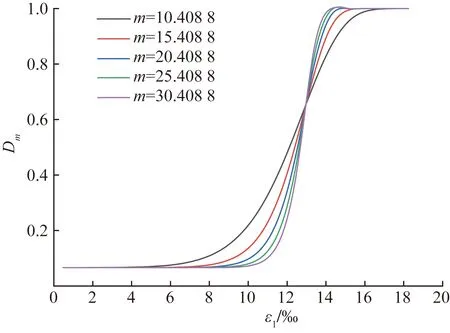
图6 参数m对总损伤Dm的影响
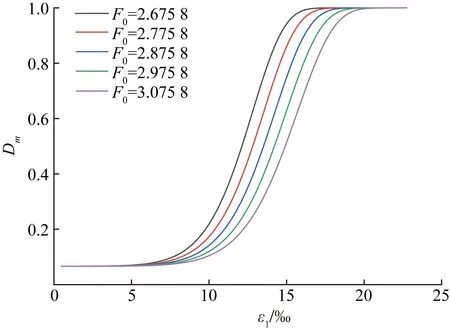
图7 参数F0对总损伤Dm的影响
由图6可知,F0不变的情况下,伴随m的增大,曲线交界点前岩石总损伤变形曲线整体向右偏移,同时,曲线交界点后曲线的斜率随m的增加而变陡,说明参数m的增大,岩石进入完全损伤时所需的应变量较小。由图7可知,m不变的情况下,伴随F0的增加,岩石总损伤演化曲线形状基本不变且曲线的斜率逐渐变缓,说明参数F0的增大,岩石进入完全损伤时所需的应变量较大。
6 结论
(1)在已有的冻融荷载耦合损伤模型基础上,基于SMP破坏准则,通过损伤阈值分段,结合残余强度的影响,构建了冻融受荷岩石统计损伤软化模型。利用岩石力学特性曲线的极值特性,利用峰值点C偏导数法确定了模型参数m和F0。
(2)通过试验结果验证了基于SMP准则的冻融受荷岩石损伤软化模型的合理性,结果表明:该模型为解决冻融受荷岩石的应变软化过程提供了思路,同时可以较好的反映岩石损伤的全过程;模型参数均可通过常规岩石力学试验获取,反映了冻融受荷岩石的损伤机制与其相关参量的一般规律。
(3)通过岩石总损伤演化分析,基于SMP准则可以反映冻融受荷岩石变形过程中宏细观损伤的一般规律,随着冻融次数及围压的增大,岩石损伤变形初期宏观表现为岩石强度减弱,岩石损伤变形进入中后期,曲线斜率减缓宏观表现为岩石抵抗变形能力减弱,并且结合 Weibull统计损伤分布中参m和F0对岩石损伤变形的影响分析,表明冻融荷载作用对岩石变形的延性和塑性特征影响更加明显。

