孔隙水中氦气溶解与脱溶量估算方法及其地质意义
赵 栋 王晓锋 刘文汇,3 张东东 李孝甫 张珈毓
1.“大陆动力学”国家重点实验室·西北大学 2.西安石油大学实验室管理处(实验中心)3.中国石化石油勘探开发研究院
0 引言
氦(He)是自然界中熔沸点最低的已知元素,也是分子直径(0.26 nm)最小的稀有气体,在国防军工、电子科技、低温科学、仪器制造等领域应用广泛,是现代高新技术产业链中无可替代的稀缺资源,享有“黄金气体”之美誉[1-3]。
He封闭温度较低,在大多数 岩石、矿物中的保留系数不超过20%[4],具有极强的扩散性和渗透性[5-7]。但自然条件下,岩石、矿物生氦强度极低,不存在类似于烃源岩的生、排烃高峰,无法独立形成连续流体,因此其运聚成藏必须借助孔隙流体完成,这也是氦气常以微量组分形式与烃类、非烃气体相伴生[8-13],或以溶解态赋存于地下水中[4,14-17]的重要原因。
目前探明具有工业价值的氦资源以壳源为主,Brown[11]提出的氦气经典成藏理论认为:He自矿物中产生后便会从矿物晶格快速析出进入岩石孔隙,并以溶解氦为主要形式在孔隙中不断聚集;当其他游离气体(如CH4)运移经过含氦孔隙、裂隙水时,溶解氦遵从亨利定律与其他气体发生“竞争性溶解”而脱溶释放,并随该气体进入圈闭形成含氦天然气藏[3,11]。
He在孔隙水中的扩散速度异常缓慢,必须通过流体的大规模运移才能实现远距离的迁移[18]。Brown经典理论着重强调了外界气体对He的“萃取”和“运载”作用,因而其很好阐释了He资源与烃类气藏的伴生性。但从水溶气溶解—脱溶角度考量,该理论并未充分讨论原位溶解氦自身赋存环境改变对He富集成藏的影响,特别是当沉积盆地大规模构造抬升引起地层温度、压力持续降低时,孔隙中的溶解氦也可自主脱溶释放形成规模性游离氦[19-20]。虽然上述认识早已被业界所关注[20-21],但目前关于构造抬升与He富集之间的关联性仍然缺少必要的数据模型加以佐证。
本次研究以单位体积花岗岩为例,通过岩石孔隙水中He溶解量、脱溶量的模拟计算,对构造抬升引起氦资源富集的有效性进行了初步定量表征,并在此基础上分析了部分气藏实例,以期为氦资源评价、开发提供有益参考。
1 He溶解度计算
1.1 He溶解度计算方法
自20世纪30年代起,惰性气体在水中的溶解度便受到了物理化学家们的极大关注。他们从液态水中的溶液分子模型、惰性气体溶解机理、水的“结晶度”等多个方面对稀有气体在水溶液中的热力学行为进行了详尽的讨论,进而提出了多种适用于不同温、压范围的惰性气体溶解度计算模型[22-23]。
Weiss[24-25]在总结、评估前人报道的N2、O2、Ar溶解度数据基础上,将溶解度数据拟合为一个平滑的函数方程,并将方程结果定义为本森系数(Bunsen Coefficient),即当气体分压(或逸度)为1 atm(1 atm=101 325 Pa)时,单位体积液体(1 cm3)可溶解的标准状态下(即压力1 atm,温度0 ℃)气体的体积(cm3),这里的气体体积可用理想气体或真实气体表示。
在随后的工作中Weiss[26]又根据He、Ne、Ar的溶解度实验数据对方程参数进行了补充修订,使其能够胜任惰性气体溶解度的计算,如式1所示。
式中β表示本森系数,L/(L·atm);T表示温度,K;S表示盐度,g/kg;A1=-34.626 1;A2=43.028 5;A3=14.139 1;B1=-0.042 34;B2=0.226 24;B3=-0.033 12。
Colt[27]在研究海洋环境时利用本森系数对惰性气体在淡水、海水中的溶解度进行了求解,如式(2)所示,并在此基础上将计算单位转化为更为常见的溶解度单位(mg/L),见式(3),使其适用于任意温、压条件下单一体系的惰性气体溶解度计算。计算结果具有良好的适用性。
式中Cp,x表示气体溶解度,L/(L·atm);βi表示本森系数;χi表示气体组分的摩尔分数;pB表示气体压力,atm;pWV表示水蒸气压力,atm。
式中Cp,x表示气体溶解度,mg/L;βi表示本森系数,由于稀有气体溶解度较低,通常用1 000β表示,如1 000βHe;pB表示气体压力,kPa;pWV表示水蒸气气压,kPa;Ki表示计算常数,He为0.178 48。
1.2 He溶解度计算结果
利用Colt[27]修正后的计算公式(式3),可对He在地层条件下的溶解度进行求解,式中气体组分摩尔分数(χi)可根据原位孔隙流体中He相对体积分数进行赋值。但统计结果表明我国中西部主要富氦气藏He原位储层孔隙中He相对含量差异显著,主要介于0.96%~6.87%[9-10,28-31],因此在研究过程中假定了1%、5%、10%共3种He摩尔分数(χHe),以充分表征不同分压条件下He溶解度的变化情况。其他地质背景参数均为通用平均值(地表温度20 ℃,地层温度梯度30 ℃/km,地层压力梯度10 MPa/km),仅孔隙水盐度因假定为淡水环境取值0 g/kg,这主要是由于目前没有资料详细介绍过地质条件下He在盐溶液中的真实溶解度或热力学模拟值,致使计算结果无法校验,增加了不确定性,加之国内主要富氦盆地地层水盐度差异较大,无类似于正常海水盐度(3.5%)的平均值可供参考,并且盐度的缺失并不会显著影响溶解度随温度、压力变化的趋势,故本次计算以淡水环境替代。
计算结果表明,地层条件下He溶解度极低,且随地层埋深及摩尔分数增加而增大(表1、图1)。
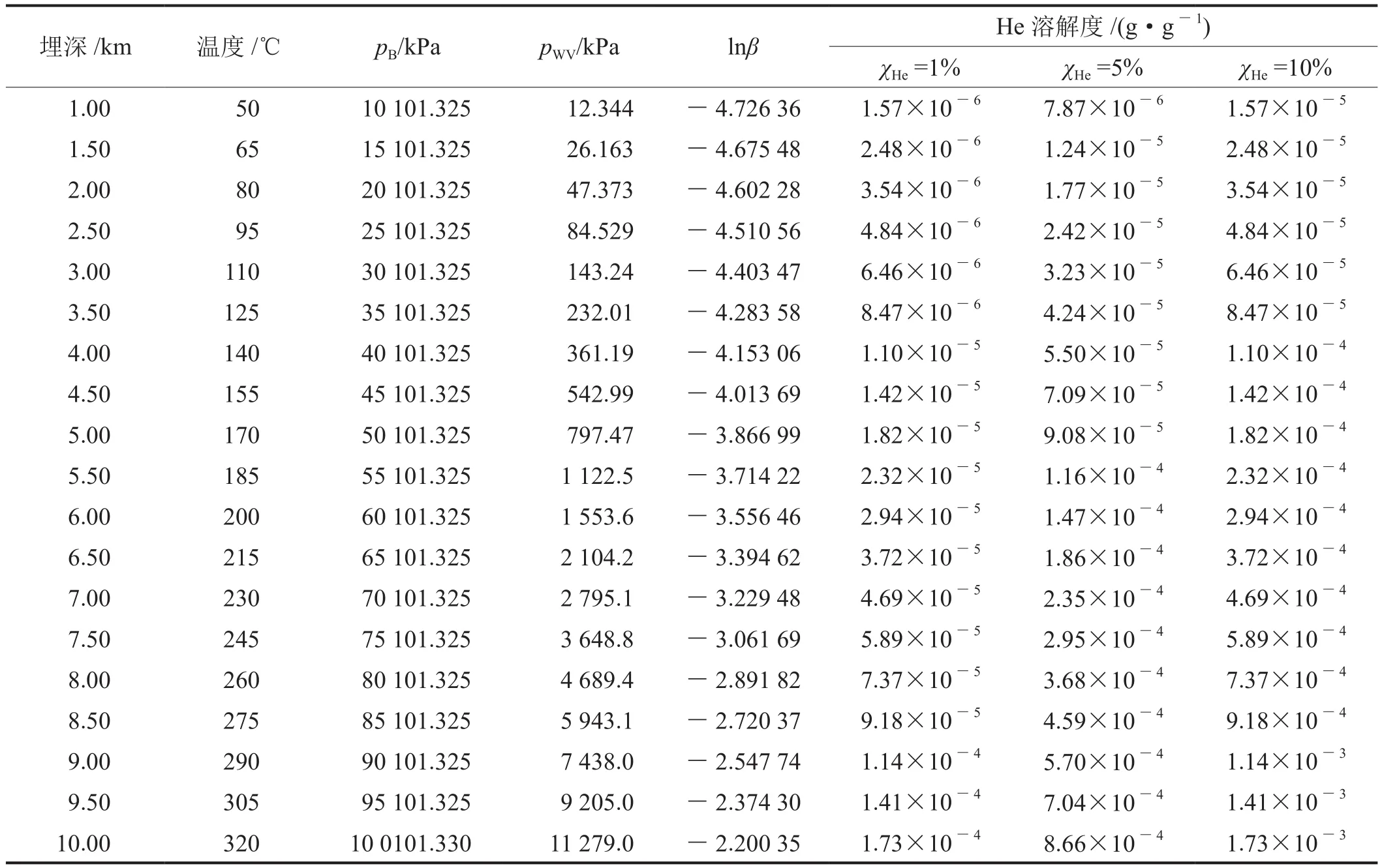
表1 地层淡水环境中He溶解度计算结果表
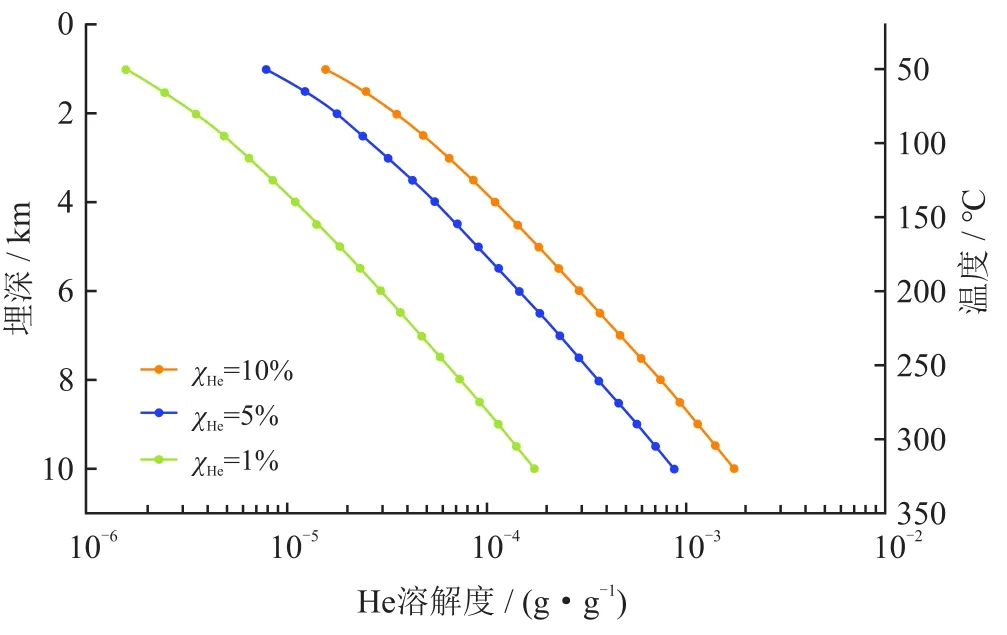
图1 地层条件不同摩尔分数下He溶解度图
自然条件下,气体在水中的溶解度通常受温度、压力、盐度和气体体积分数共同影响,但在地层环境中,由于气体体积变化巨大,分压往往会成为影响气体溶解度变化的主控因素,稀有气体更是如此[17]。He溶解度计算结果也证实χHe对溶解度变化有着更为显著的影响,如当χHe为1%时,在浅表区域He溶解度仅为10-6g/g量级,随埋深增大,溶解度虽有所改善,但也仅为10-5~10-4g/g量级;而当χHe增大至10%时,在相同埋深范围内,溶解度可突破10-3g/g量级,具有更宽广的变化幅度。
2 孔隙水中He溶解量、脱溶量计算
2.1 He溶解量与原位赋存状态
在溶解度基础上,可对岩石孔隙水中He溶解量进行计算,但仍需明晰He累积产量,方能探讨He原位赋存状态。He在天然气成藏过程中具有明显的年代累积效应[6],其形成与累积主要受控于源岩矿物中U、Th元素的含量及衰变发生的累积时间。但目前关于壳源富氦气藏中氦资源的源岩类型还存在不同认识,争议主要集中在相对富含U、Th的泥页岩与年龄古老的基底花岗岩之间[2]。业内主流观点认为以泥页岩为烃源岩的天然气藏中并未形成广泛的氦气富集[3],发育于盆地基底或周缘的花岗岩更可能是壳源富氦气藏氦资源富集的有效源岩[28]。譬如美国堪萨斯隆起的前寒武纪花岗岩结晶基底就为世界最大的富氦天然气藏Hugoton-Panhandle气田的He充注提供了不竭来源,又如我国中西部四川、渭河、柴达木、塔里木等主要富氦盆地的内部及周缘也多有花岗岩结晶基底或花岗岩露头发育[5,9-10,29-30]。
基于以上认识,选取单位体积(1 km3)花岗岩作为模拟计算载体,首先计算其在一定时间跨度内(10~1 000 Ma)的氦气累积量,而后在溶解度基础上探讨不同埋深、不同摩尔分压条件下孔隙水中的He溶解量,从而定量表征He原位溶解状态。相关计算参数取值及来源如表2所示。

表2 溶解量计算参数表
计算结果(表3)表明,He摩尔分压与地层埋深对He溶解量具有控制性影响。以400 Ma的He累积量为例(图2):①当χHe为1%时,孔隙水中He溶解量非常有限,地层埋深6.5 km,孔隙水仅能完全溶解单位体积花岗岩100 Ma累积的氦气,埋深增加至9.5 km时,方可溶解400 Ma的氦气累积量;②当χHe为5%时,He溶解度有所提高,埋深至3 km时便可完全溶解同体积花岗岩100 Ma累积的氦气,埋深增加至6.0 km时,1 km3花岗岩400 Ma累积的氦气已完全溶解;③当χHe提高至10%时,He溶解量进一步增大,相同条件下100 Ma累积的氦气在埋深2 km时即可全部溶于孔隙水中,埋深增大至4.5 km时,孔隙水即使溶解了400 Ma累积的全部氦气也未至饱和状态。

表3 单位体积(1 km3)花岗岩孔隙水中He溶解量表

图2 单位体积(1 km3)花岗岩He累积量与溶解量计算对比图
2.2 He脱溶量
溶解量计算结果表明,倘若沉积盆地持续稳定接受沉降,且没有外界流体干扰时,溶解He比例将随地层埋深和衰变累积时间增加而增大,直至完全溶解于孔隙水中。而当沉积盆地发生大规模构造抬升时,原先赋存于孔隙水中的溶解He又会随之脱溶释放,造成赋存相态发生改变,从而为He运移提供充足的游离He源。
为了进一步验证构造抬升与He富集成藏之间的关联性,研究又以0.5 km为单位幅度,逐次计算了单位体积(1 km3)花岗岩在抬升过程中能够脱溶释放的游离He含量(表4),从而定量表征He赋存相态的比例变化。仍以累积衰变时间400 Ma,χHe=5%为例:当地层埋深大于6.0 km时,花岗岩累积产生的He可完全溶于孔隙水中;随地壳抬升,埋深至4.0 km时,已有约60%氦气从水中脱溶进入游离态;如果此后地层持续抬升,游离He含量还将快速增加,至地表附近可超过95%,接近完全脱溶(图 3)。
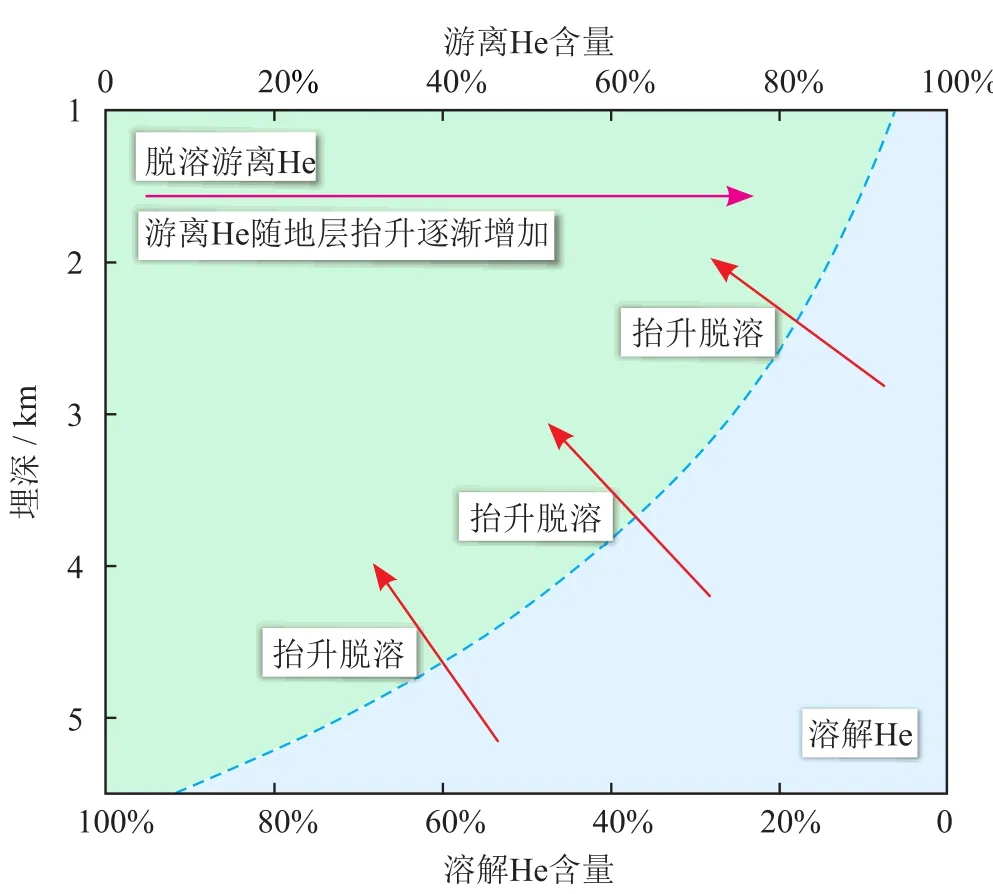
图3 单位体积(1 km3)花岗岩孔隙中He(χHe=5%)赋存相态随地层抬升变化示意图

表4 单位体积(1 km3)花岗岩抬升过程中He(χHe=5%)脱溶量表
计算模型表明,相较He与其他气体间“竞争性溶解”,大幅度的构造抬升完全可以独立引起溶解氦大规模、连续性脱溶,从而为富He气藏的形成提供稳定、高效的游离氦源。这也与美国矿务局一项关于全美天然气藏氦气含量的统计结果相一致,即在所有含氦天然气藏中,He相对富集在同一储层的较高位置,He含量随储层埋深增大而减少[34]。
3 地质意义
体积巨大的花岗岩体经过长时间累积产生的4He,可在适当条件下从孔隙水中脱溶释放,并与烃类气藏复合成藏是目前已发现富氦天然气藏的主要成藏模式[11-13,21]。基于前述计算和讨论,依据溶解氦脱溶富集过程中是否发生规模性构造抬升,可将壳源富氦天然气藏成藏模式划分为抬升脱溶型和置换脱溶型。
3.1 抬升脱溶型
抬升脱溶型氦气藏强调富氦气藏中游离氦主要来自盆地大幅构造抬升引起的溶解氦脱溶释放。我国最早开展,也是目前唯一开展工业提氦的威远气田是该类型的典型代表。
威远气田与邻近的安岳气田同处四川盆地乐山—龙女寺古隆起周缘,但He含量差异显著。威远气田平均He含量1 598 ppm(1 ppm=1 μg/g),安岳气田多数样品He含量仅为103~539 ppm。运用孔隙水He溶解、脱溶量模型计算结果,认为威远气田He资源富集及其与安岳气田He含量间的差异均与盆内构造隆升密切相关。
乐山—龙女寺古隆起早在桐湾期(震旦纪晚期—早寒武世)就已形成威远—资阳和高石梯—磨溪两个相互独立的巨型古隆起[35],而后历经海西、印支、燕山等多期构造运动,直至喜马拉雅期遭受强烈挤压,才隆升为大型穹隆背斜[35-36]。喜马拉雅期地壳的急剧抬升(41.0~107.2 m/Ma),使原本处于资阳圈闭南翼的威远地区快速隆升成为新的构造高点,并捕获来自资阳古气藏的天然气,资阳古背斜自此逐渐萎缩为威远背斜翼部[37-39],从而形成如今的威远气田。
经此构造改造,威远地区累计抬升近4 600 m,并与高石梯—磨溪地区形成了2 000 m以上的高差[37,40]。在隆升过程中,地层能量场(温度、压力)大幅减小,深埋状态下赋存于孔隙水中的溶解He得以大量脱溶,游离He从异常高压区向正常压力区转移,并与向上运移的烃类气体形成新的溶解平衡(图4)。
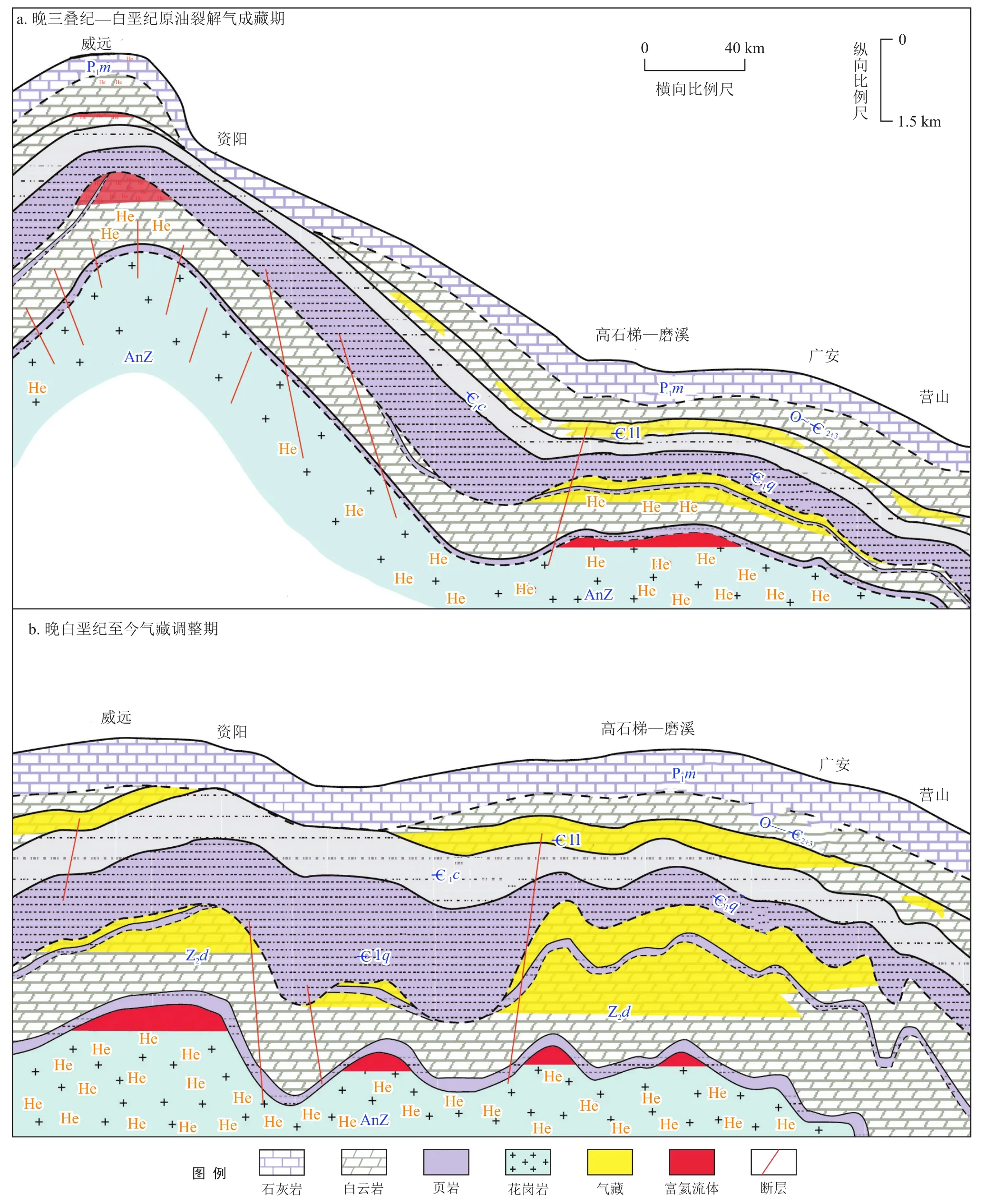
图4 四川盆地威远、安岳气田He差异富集示意图
相比之下,安岳气田虽同处乐山—龙女寺古隆起,成藏条件也与威远气田基本一致,但由于长期处于古隆起轴部[35,40],构造环境相对稳定,不具备He规模性脱溶释放的必要条件,加之气藏规模巨大(截至2019年底,三级储量为1.23×1012m3)[41],本就稀少的游离He又被烃类气体充分稀释,最终造成氦资源相对匮乏。
3.2 置换脱溶型
置换脱溶型氦气藏是指富氦天然气藏中的游离氦主要来自外界流体(主要为CH4)运移经过富氦孔隙、裂隙水时发生的置换脱溶。柴达木盆地首个发现的具有工业提氦价值的东坪气田就与该机理密切相关。
东坪气田位于柴达木盆地阿尔金山前东坪斜坡,是我国迄今发现的最大基岩型气藏。气藏平面上可分为东坪1井区和东坪3井区,天然气主要储集于古近系下伏基底结晶岩系的岩浆岩或变质岩裂缝中,依靠阿尔金山前东段的深大断裂与下侏罗统高—过成熟烃源岩沟通[10,42](图5)。
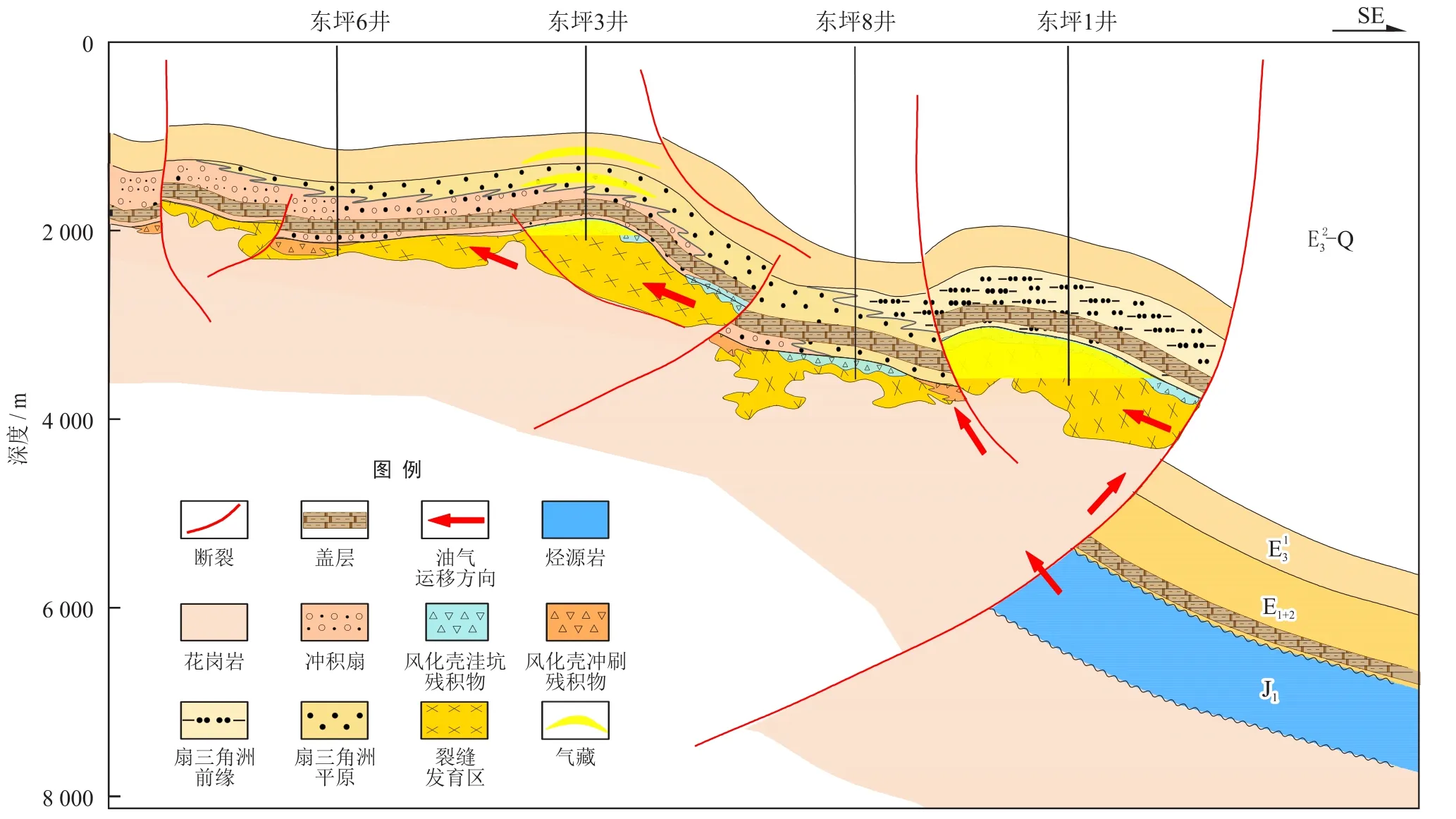
图5 柴达木盆地东坪气田成藏模式图[10]
东坪气田He平均含量0.386%,3He/4He介于(1.01~2.21)×10-8,具有明显的壳源属性,盆地基底广泛发育的花岗岩及花岗片麻岩被认为是He的主要源岩[10,30]。天然气自东南向西北沿基岩不整合面向隆起及斜坡区运移过程中,不断与基岩储层中溶解氦接触并发生置换脱溶,天然气运移距离越远,脱溶游离He含量越高(东坪1井区平均He含量0.07%,东坪3井区平均He含量0.49%),加之上覆古近系路乐河组含膏泥岩对He具有良好的封盖作用,从而形成氦资源有效富集。
4 结论
1)地层条件下He溶解度极低且变化幅度宽广,其变化主要受控于储层埋深(温度、压力)及自身摩尔分压的改变,通常情况下He溶解度随埋深及分压增大而增大。
2)目前探明具有工业价值的氦资源主要以壳源为主,花岗岩是壳源富氦天然气中氦的主要源岩,通过建立花岗岩孔隙水He溶解、脱溶量计算模型,认为大幅度构造抬升能够引起溶解氦持续性、规模性脱溶,从而为富氦气藏提供充足的游离氦源。
3)体积巨大的花岗岩体经过长时间累积产生的4He,可在适当条件下从孔隙水中脱溶释放。依据孔隙溶解氦脱溶富集过程中是否发生规模性构造抬升,将壳源富氦天然气藏成藏模式初步总结为抬升脱溶型和置换脱溶型。

