高危行业企业安全投入与员工安全行为策略演化博弈分析*

谢友财

(广州华商学院，广东 广州 511300)

0 引言

安全生产是企业生产经营管理的重中之重，尤其是对于煤矿、建筑等高危行业而言，安全生产愈发重要。随着国家和企业日益重视安全生产，并积极采取多种措施保障安全生产，安全事故发生率显著降低，但每年依然会发生多起安全事故，造成重大财产损失及人员伤亡。因此，如何进一步降低安全事故发生率、保障员工作业安全、促进企业安全高效生产是当前面临的重要课题。

一般认为，影响安全生产的因素主要包括安全文化、安全科技、安全法制、安全投入、安全责任五方面，这五方面因素往往是既相互独立，又相辅相成，互为前提条件。其中，安全投入是指因安全活动需要所投入的各种人力、物力、财力等资源的总和，主要包括安全设施设备、安全科学技术、安全专业人员等。安全投入是安全生产的基本保障，但也会带来企业运营成本的增加。基于此，诸多学者针对安全投入对安全生产的影响进行了研究。陈淑婷[1]分析了安全生产五要素间的逻辑关系，通过实地调研认为加大安全投入可以有效提高企业本质安全水平。李振等[2]针对煤矿企业安全投入不足及不合理的问题，提出了集成支持向量机和连续蚁群算法的安全投入模型，以寻求最优安全投入。曹秀兰等[3]通过构建结构方程模型，进行不同安全投入的方式与策略对工人安全绩效影响关系验证，提出提高建筑工人安全绩效的有效途径。杨玉梅等[4]通过寻求优化安全投入方法，提出了基于GA-SVR-PSO的航运安全优化模型，可为企业安全投入决策提供参考。冯领香等[5]通过构建代理模型探索了安全投入优化方法，指出增加安全投入虽然可以有效提升安全绩效，但边际递减效应明显。上述研究基本涵盖了安全投入对安全生产的作用、安全投入的优化方法、安全投入的优化途径三方面，提出了相关优化改善方法和措施，基本明晰了安全投入对企业安全生产的作用机制，为企业预防安全事故奠定了理论和方法基础。

在预防安全事故发生的途径中，仅依靠加大安全投入是不足够的，因为人员既是安全事故的受害者，也是安全事故的致因者。相关统计资料表明，人员的不安全行为导致的安全事故比例高于其他原因导致的安全事故比例，成为安全事故发生的主要原因之一，因而成为预防安全事故发生的重要研究方向。人员不安全行为一般是指因人为错误而导致事故发生，主要包括违规操作、使用不安全设备、违反劳动纪律等。许多学者针对人员不安全行为进行了研究。叶贵等[6]基于ISM法构建了不安全行为影响因素的三层四阶递阶结构模型，对建筑工人不安全行为的发生机理进行了探究。朱艳娜等[7]从煤矿安全事故致因中选取影响因素，构建了结构方程模型，分析了矿工不安全行为与影响因素的关联系数。张倩等[8]从组织公平的角度，基于结构方程模型构建了组织公平对矿工不安全行为的理论模型，认为增强组织公平感可以有效降低不安全行为。马琳等[9]通过构建多群组结构方程模型，探究了有感领导(有安全认知的领导)对不同文化程度矿工不安全行为的影响。从上述学者的研究中可以看出，针对人员不安全行为的研究主要是从不安全行为发生机制、影响不安全行为发生的因素识别、组织环境与人员不安全行为的关联关系等方面，为改善员工不安全行为、预防安全事故的发生提供了理论参考和依据。

企业安全投入的增加及人员不安全行为的改善，可以在一定程度上减少安全事故的发生，降低安全事故发生率，提高企业安全效益。对于企业来说，增加安全投入意味着增加企业的运营成本；对于员工来说，改善不安全行为意味着增加作业负荷。因此，对于企业和员工而言，不管采取哪种策略都会权衡所选择的策略给自己带来的收益得失。演化博弈理论正是以博弈者的有限理性为基础，当博弈双方无法准确判断自身在博弈过程中的状态时，把博弈理论分析和动态演化过程分析结合起来最终达到稳定变化的过程[10]，是研究多行为主体策略演化的有效方法。演化博弈理论已在人员不安全行为研究中得到应用。陈艳等[11]对动态视角下的建筑工人不安全行为进行了演化博弈分析，指出提高安全奖励的额度、加大对不安全行为的惩罚力度、采用与不安全行为收益相关的动态惩罚策略，均能降低建筑工人不安全行为发生概率。郑霞忠等[12]对起重作业人员有意不安全行为致因进行了多方博弈分析，认为作业人员进行决策时权衡风险、成本、收益及各方意见，能够有效减少作业人员有意不安全行为的发生。

而作为安全生产的基本保障要素之一的安全投入与作为安全事故发生的主要致因之一的人员不安全行为之间是否存在某种关联，增加安全投入是否可以促进员工不安全行为的改善，进而达到提高安全效益的目的，是企业需要进一步研究的重点。目前，针对企业安全投入与员工不安全行为间影响关系的研究较少，所能参考的文献有限。基于此，本文从企业和员工双方选择策略的利益出发，将演化博弈理论引入安全生产领域，根据演化博弈理论构建以企业和员工为主体的策略选择动态演化博弈模型，分析企业安全投入与员工不安全行为的演化规律，进行数值仿真分析，进一步分析员工不安全行为策略的变化对企业安全投入的影响，并提出相应改善建议，为企业做出合理决策提供参考。

1 企业安全投入与员工安全行为演化博弈模型的构建

1.1 模型的假设

假设1：企业采取的策略只有两种，即增加安全投入和不增加安全投入；员工采取的策略也只有两种，即采取安全行为和采取不安全行为。两个博弈主体的策略均不存在其他情形。

假设2：企业不增加安全投入时，固定收益为R，企业增加安全投入的成本为C，企业因增加安全投入带来的额外收益为R1，员工的固定收益为R3，企业增加安全投入时员工采取安全行为获得额外效益为R2，员工不安全行为导致安全事故发生概率为q，安全事故给企业带来的损失为D，企业和员工安全事故损失承担比例为f1、f2，企业因安全事故受到上级部门罚款为I1，员工因不安全行为导致安全事故被企业罚款为I2，企业不增加安全投入时因员工不安全行为导致安全事故需投入额外资金R4进行修护。

1.2 博弈主体收益矩阵的建立

根据上述假设，计算各博弈主体采取不同策略时的收益。

1.2.1 企业增加安全投入

(1)员工采取安全行为时，企业收益为R+R1-C，员工收益为R2+R3。

(2)员工采取不安全行为时，企业收益为R+R1-C-q×(f1×D+I1)，员工收益为R3-q×(f2×D+I2)。

1.2.2 企业不增加安全投入

(1)员工采取安全行为时，企业收益R，员工收益为R3。

(2)员工采取不安全行为时，企业收益为R-q×(f1×D+I1+R4)，员工收益为R3-q×(f1×D+I2)。企业和员工的收益矩阵见表1。

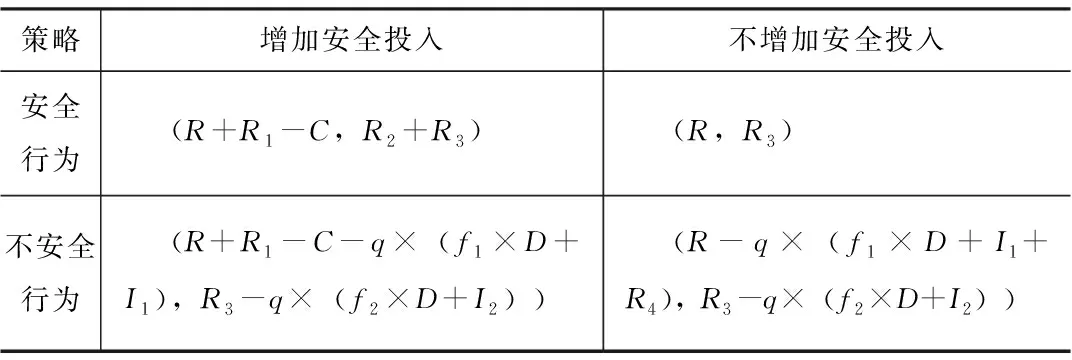
表1 企业和员工收益矩阵

1.3 演化博弈模型求解与分析

根据企业和员工收益矩阵，构建各博弈主体的演化博弈复制动态方程。假定企业和员工在选择策略过程中相互独立，互不干扰。企业选择增加安全投入的概率值为x，则选择不增加安全投入的概率值为1-x。员工选择安全行为的概率值为y，则选择不安全行为的概率值为1-y。企业选择增加安全投入时期望收益为Eqi，不增加安全投入时期望收益为Equi，企业的平均期望收益为Eq。计算公式如下

Eqi=y(R+R1-C)+(1-y)[(R+R1-C)-q×(f1×D+I1)]=q(y-1)(f1×D+I1)+(R+R1-C)

(1)

Equi=y×R+(1-y)×[R-q×(f1×D+I1+R4)]=q(y-1)(f1×D+I1+R4)+R

(2)

Eq=x×Eqi+(1-x)×Equi=(y-1)(f1×D+I1+R4)-xq(y-1)R4+x(R1-C)+R

(3)

同理可得员工选择安全行为的期望收益Eks，选择不安全行为的期望收益Ekus，员工的平均期望收益Ek。计算公式如下

Eks=x(R2+R3)+(1-x)R3=xR2+R3

(4)

Ekus=x×[R3-q×(f2×D+I2)]+(1-x)[R3-q×(f2×D+I2)]=R3-q(f2×D+I2)

(5)

Ek=y×Eks+(1-y)×Ekus=xyR2+q(y-1)(f1×D+I2)+R3

(6)

博弈主体在选择策略时会根据环境及条件的变化随时调整选择的策略，因此会产生一个时间上连续的总体动态，称之为动态复制方程[13]。根据博弈主体的各策略期望收益，可得各博弈主体的复制动态方程。企业选择增加安全投入策略的动态复制方程记为F(x)，员工选择安全行为策略的动态复制方程记为F(y)。则

(7)

(8)

令F(x)=0，F(y)=0组成微分方程组进行求解，可得博弈主体策略选择演化系统的5个均衡点，分别为

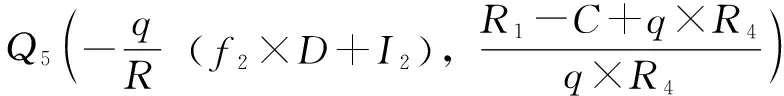
根据Friedman理论，当一个群体状态由微分方程组描述时，则可用该系统的雅克比矩阵的局部稳定性描述分析该系统均衡点的稳定性[14]。因此，F(x)，F(y)分别对x，y进行求偏导数，得到企业和员工策略演化博弈系统的雅克比矩阵J，如下

(9)

当演化博弈系统的均衡点满足雅克比矩阵的行列式DetJ=|J|>0，迹trJ<0时，则该均衡点为局部稳定状态，反之则不是局部稳定状态。其中DetJ和trJ的计算公式如下

DetJ=(1-2x)(1-2y)[R1-C+(1-y)qR4]×[xR2+q(f2×D+I2)]+xyq(x-1)(1-y)R2R4

(10)

trJ=(1-2x)[R1-C+(1-y)qR4]+(1-2y)[xR2+q(f2×D+I2)]

(11)

将企业和员工策略演化博弈系统的5个均衡点代入DetJ和trJ公式中进行计算，依据其结果符号判断是否处于局部稳定点ESS，结果见表2。

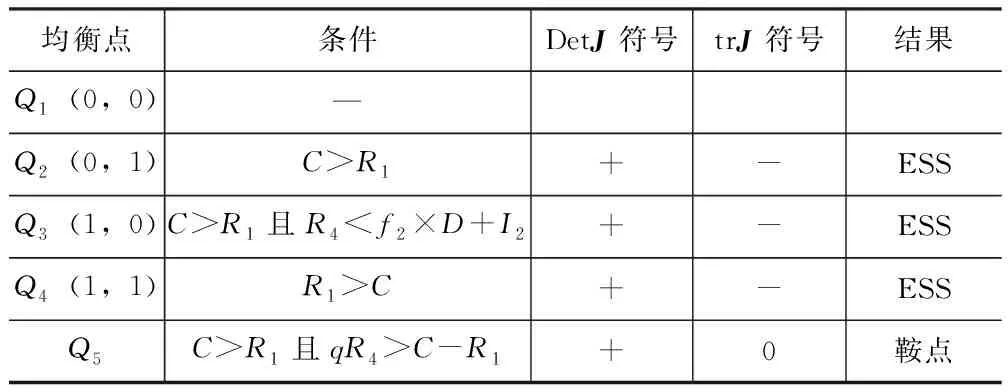
表2 局部稳定性分析

从表2可以看出，企业与员工策略选择演化博弈系统中具有3个局部稳定点，企业和员工稳定演化策略为：

(1)当系统稳定于Q2(0，1)时，即企业选择不增加安全投入、员工采取安全行为，此时为低安全投入成本、低安全行为成本模式。

(2)当系统稳定于Q3(1，0)时，即企业选择增加安全投入、员工采取不安全行为，此时为高安全投入成本、高安全行为成本模式。

(3)当系统稳定于Q4(1，1)时，即企业选择增加安全投入、员工采取安全行为，此时为高安全投入收益、低安全行为成本模式。

2 企业安全投入与员工安全行为演化博弈模型数值模拟

为进一步分析博弈双方选择策略过程的影响作用，根据企业和员工策略选择的动态复制方程对企业和员工策略选择演化过程进行数值模拟，分析博弈双方选择某策略时的概率值对双方策略演化博弈过程的影响。

2.1 企业策略选择演化博弈数值模拟

在表2中的3个均衡点中，由于Q2(0，1)和Q3(1，0)均衡点的条件近似一致，只选择Q3(1，0)和Q4(1，1)均衡点进行数值模拟。假定R2=4，q=0.3，f2=0.4，f1=0.6，D=10，I2=8，t=30，R4=11。

(1)当位于Q3(1，0)均衡点时，取C=6，R1=5，分别选取员工选择安全行为策略概率值y=0.3，y=0.7进行数值模拟，结果如图1所示。

从图1a可以看出，当员工选择安全行为策略概率值较低时，企业最终会做出选择增加安全投入策略决策，即使此时因安全投入的收益小于安全投入成本。从图1b可以看出，当员工选择安全行为策略的概率值较高时，企业选择增加安全投入的概率值随着时间的推移将逐步降低。因此，员工选择安全行为策略的概率值显著影响企业选择增加安全投入策略决策。

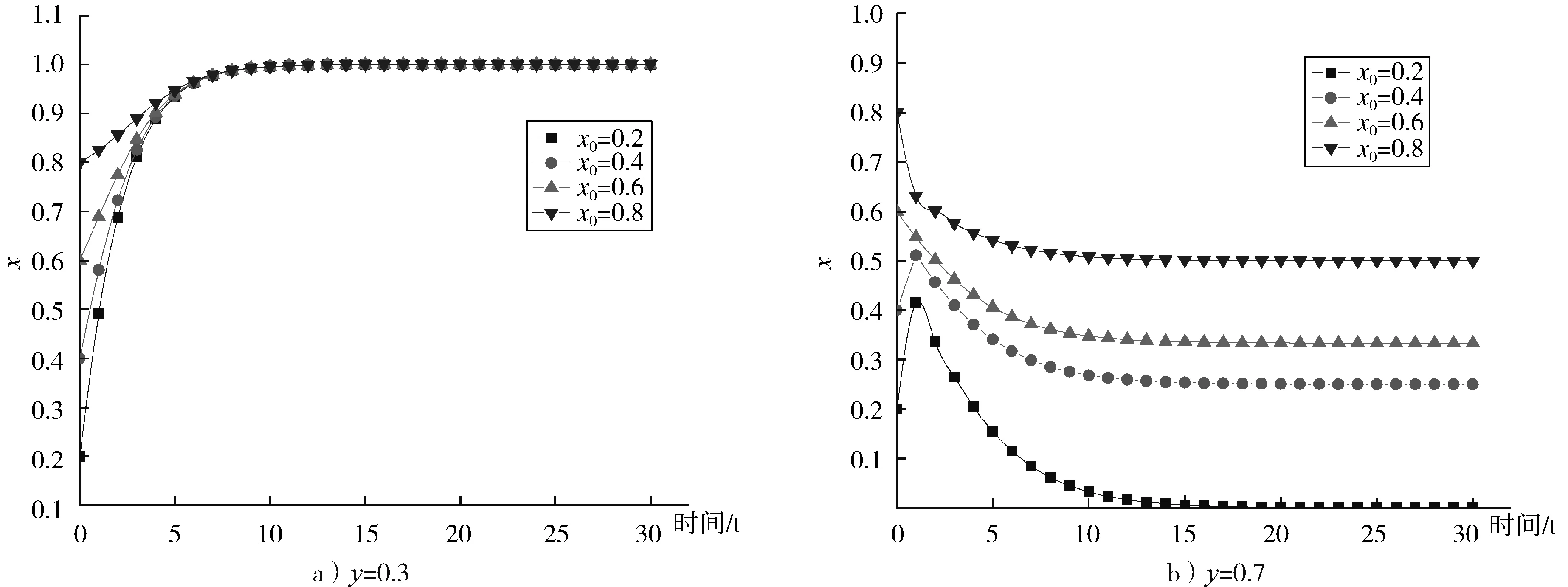
图1 Q3(1，0)均衡点企业策略演化博弈数值模拟

(2)当位于Q4(1，1)均衡点时，取C=5，R1=6，分别进行y=0.3，y=0.7数值模拟，结果如图2所示。从图2可以看出，员工选择安全行为策略的概率值对企业选择增加安全投入概率值没有影响，企业都会选择加大安全投入，此时对于企业来说，加大安全投入所获收益大于加大安全投入成本。因此，当企业加大安全投入有利可图时，员工选择安全行为的概率值对企业的策略选择没有影响。

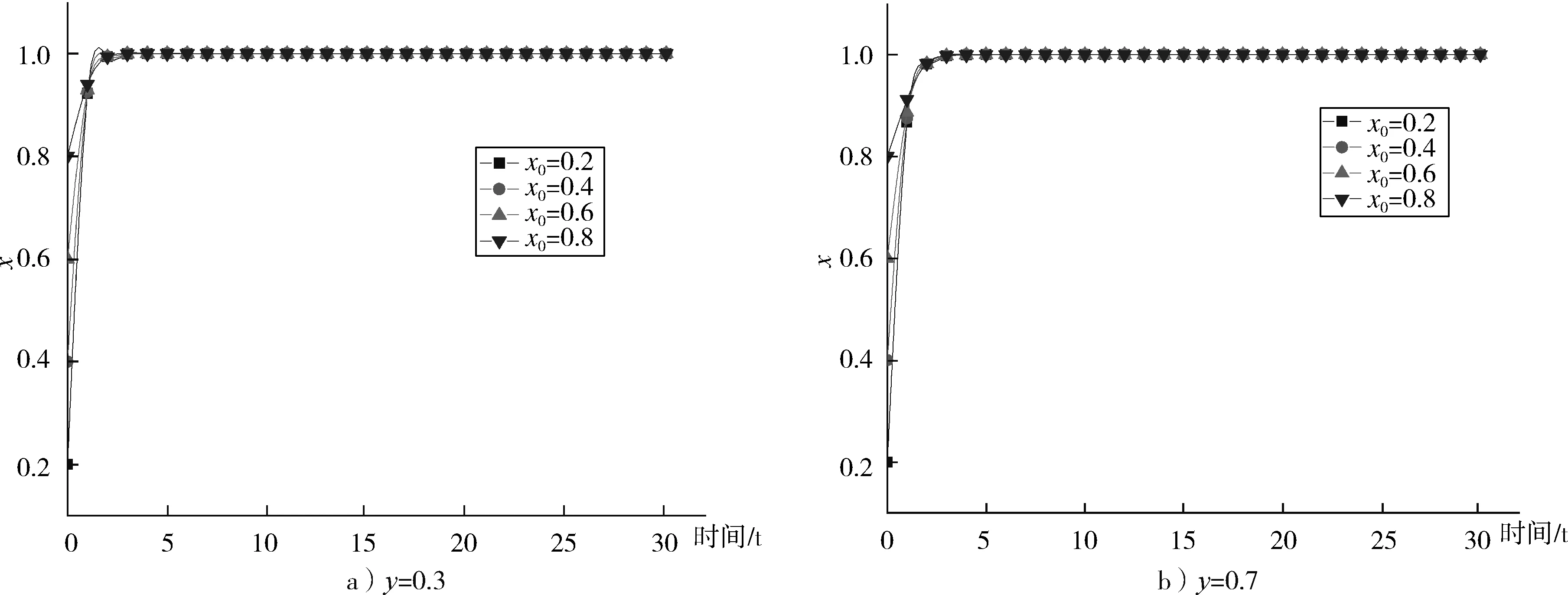
图2 Q4(1，1)均衡点企业策略演化博弈数值模拟

2.2 员工策略选择演化博弈数值模拟分析

从企业和员工策略选择的演化博弈3个均衡点可以看出，每个均衡点涉及员工策略选择的条件均一致，因此选择Q3(1，0)均衡点进行员工策略选择演化博弈数值模拟。根据2.1中各变量的取值以及员工策略选择的动态复制方程，选取企业选择增加安全投入概率数值x=0.3，x=0.7进行数值模拟，模拟结果如图3所示。从图3可以看出，企业增加安全投入的概率值的改变对员工选择安全行为策略没有影响，即无论企业是否加大安全投入，员工均选择安全行为策略。

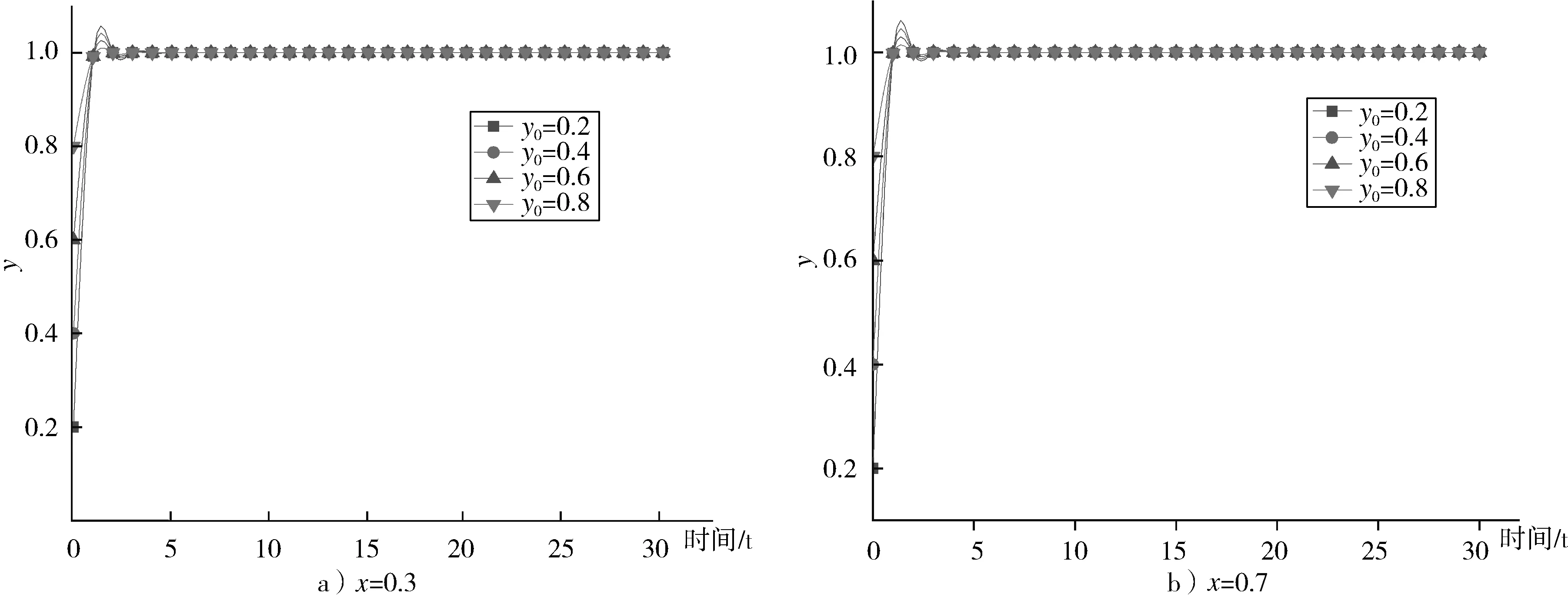
图3 员工策略选择演化博弈数值模拟

3 结语

安全投入是企业安全生产的基础，人员安全行为是减少安全事故发生的重要途径。为进一步探究企业安全投入决策与员工安全行为间的影响关系，本文从传统博弈理论的角度建立了企业安全投入与员工安全行为的演化博弈模型，并进行了数值模拟分析，可为企业和员工策略选择提供参考。结论及建议如下：

(1)当企业加大安全投入所获收益小于安全投入成本时，员工采取安全行为策略的概率值将显著影响企业策略选择决策。此时，企业要加大对员工的安全教育培训，或采取必要措施督促员工采取符合作业安全规范的行为，以降低企业成本、减少安全事故的发生。

(2)当企业增加安全投入的收益大于安全投入成本时，员工采取何种策略均不影响企业选择增加安全投入。此时，企业可以通过适当地给予员工安全奖励、提高员工福利等措施鼓励员工安全作业，减少安全事故的发生。