面向大变形测量的数字图像相关方法的研究进展及应用

李佳成，叶敬晨，计宏伟

面向大变形测量的数字图像相关方法的研究进展及应用

李佳成a，叶敬晨b，计宏伟b

（天津商业大学 a.生物技术与食品科学学院 b.机械工程学院，天津 300134）

探究数字图像相关方法（Digital Image Correlation, DIC）对大变形测量问题的研究现状，为相关领域展开深入研究提供参考。通过对增量相关、初值估计和形函数等方面的改进梳理，总结研究人员关于DIC方法在大变形测量问题的研究进展。现有的DIC方法研究大变形测量问题，主要通过增量方法以及结合特征检测的初值估计方法，极大地消除了去相关效应，同时对形函数的选择和结合深度学习等技术也增强了DIC方法对复杂变形的适用性。尽管面向大变形测量的DIC方法面临着诸多挑战，但DIC方法仍然是极具潜力的大变形测量技术之一，DIC方法在大变形测量中将发挥更重要的作用。

数字图像相关法；大变形测量；形函数；初值估计

随着包装材料[1]、软材料[2-3]、多孔材料[4-5]、航空航天材料[6]、复合材料[7-8]、生物材料[9-10]等新型材料的广泛使用以及应用场景的扩宽，探究材料在大变形条件下的力学性能和力学行为逐渐成为研究热点，实现准确的大变形测量极为重要。工程领域中广泛应用的变形测量技术分为2类[11]：一类是以电阻应变片为代表的接触式测量方法，具有量程大、灵敏度高、应用范围广等优点[12]，但无法测量全场变形；另一类是全场的非接触式光学测量方法，包括数字云纹法[13]、散斑干涉法[14]、数字图像相关测量法（Digital Image Correlation，DIC）[15-16]等。其中DIC方法由于具有设备简单、全场测量、适应性广、精度高等突出优点，已经成为现代光测力学中受欢迎的变形测量方法之一，在实验力学[17]、材料科学[18]、生物力学[19]等许多领域中广泛使用。

DIC方法的开创性工作可以追溯到20世纪80年代，由Peters等[15]和Yamaguchi[16]首次提出，后经过国内外学者的研究和完善发展，其方法已经相当成熟。然而，DIC方法在大变形的测量问题中仍然面临挑战，受到退相关效应、累计误差、形函数欠匹配等问题的严重干扰。尽管如此，DIC技术仍然是大变形测量中最具潜力、最具价值的测量方法。进一步提高DIC方法的大变形测量能力以应对日益复杂的变形测量需求。本文首先介绍DIC的基本原理，然后回顾并评述DIC方法在大变形测量问题中的进展和应用，最后总结当前面临的挑战和可能突破的方向。

1 DIC方法的基本原理

DIC方法的基本测量过程如下：首先在被测试样表面制作散斑，使用相机采集被测试样表面变形前后的连续散斑图像作为参考图像与变形图像，然后使用局部（基于子区）或全局（基于有限元）方法[20]通过跟踪子区灰度分布获得子区的位移，如图1所示，从而得到对应的位移场，最后使用合适的数值微分方法从位移场中提取应变场。经典的DIC算法包含2个关键步骤：首先使用整像素搜索算法寻找整像素精度的位移初值，再通过亚像素配准方法将其精确到亚像素精度。亚像素配准方法分为拟合法和迭代法2种。其中，迭代法被认为是DIC方法获得高测量精度的关键，其涉及的优化问题通常是非凸的，因此需要良好的位移初值作为收敛性的保证。

图1 DIC方法基本原理

2 大变形测量的关键问题

由于试样变形前后图像过大的差异和随变形程度增大而逐渐严重的退相关效应，DIC方法在大变形测量问题中仍然面临挑战，其主要困难集中在退相关效应和形函数欠匹配两方面，特别是在复杂变形的测量中。

2.1 退相关效应

DIC方法获得可靠初值估计的关键是相关系数分布的单峰性，如图2a所示，真实位移附近的相关系数明显高于其他位置。在大变形测量中，由于图像的差异过大，真实位移附近的相关系数急剧减小，如图2b所示，有效的初值被淹没在局部极值中而无法通过相关匹配正确求解。同时相关子区的选取中，大旋转也可能会引起严重的退相关效应。此外，大变形问题可能会伴随着较大的离面位移，焦距、视角的改变也是退相关效应的重要来源。

图2 典型的相关系数分布

2.2 欠匹配问题

DIC方法通过形函数近似子区内部变形以提高测量的准确性。零阶形函数仅包含位移分量，用于表征平移变化；一阶形函数增加了应变分量，能够表征平移、伸缩、旋转、剪切及其复合。在大变形问题中，尤其是复杂变形问题中，一阶形函数不足以描述子区内部变形，形函数与真实变形欠匹配。较高的欠匹配程度增大了亚像素迭代的系统误差，甚至导致无法收敛，同时裂纹、界面处变形的强弱不连续性也会导致较大的欠匹配问题。

3 大变形测量的研究进展

为了克服大变形测量问题中的关键问题，Zhang等[21]指出2个关键因素：一是足够接近真值的初值估计，二是足够合适的形函数。基于这2个关键的解决因素，研究人员做了许多不同的研究。

3.1 增量相关策略

尽管DIC方法在大变形测量问题中具有困难，但是实际上采用增量相关策略[22]很容易避免大变形问题的出现。如图3所示，通过增大图像采集的频率以捕捉更细微的变形过程，使得相邻2幅图像的变形可以视为小变形。这意味着，其增量变形的测量仍然可能处于DIC方法的测试范围内，实际变形场是增量位移场的累积。然而遗憾的是，测量误差在每一阶段的相关过程中被累积，这导致了可能过高的测量误差，使最终的测量结果严重偏离实际值。其中累积误差来源于子区偏移和插值误差这2个方面。

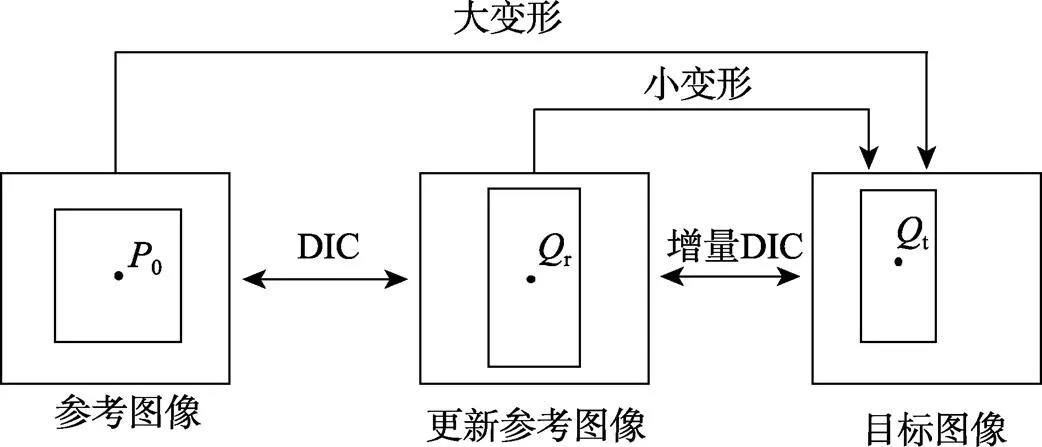
图3 增量相关原理

子区偏移是累积误差最主要的来源。由于每次增量测量的误差，变形子区与其真实值存在微小的差距，在更新参考图像后，新的参考子区与原始参考子区并不完全相同，从而产生偏移，即使每一阶段的测量误差都很小，也无法完全保证位移场累积后的测量精度。累积误差的大小依赖于参考图像的更新次数。为了避免过大的累积误差，Pan等[22]通过设定相关系数的阈值控制参考图像的更新，这一策略获得了广泛的使用。另一种高可靠的策略是避免对参考图像的直接更新，Tang等[23]认为引入增量相关的中间图像可以用来辅助计算第阶段的图像和参考图像之间的相关性，但不能直接作为参考图像使用，因此使用第−1阶段的相关参数对参考子区进行重塑，重塑后的参考子区进行之后的相关计算，同时应用ILS算法的标准偏差来判断是否需要更新参考图像，将改进的粗略搜索方法与更新参考图像的方法相结合，不但可以成功地测量极大的变形，而且参考图像的更新次数也减少到最小，从而控制了累积误差。

插值误差是累积误差的次要来源。插值误差会不可避免地引起额外的系统误差。为了解决这一问题，Zhou等[24]对增量相关方法进行改进，提出将更新的参考子区转换到最近整数位置的自适应子区偏移方法来消除插值误差；之后Wang等[25]应用同样的思想提出了最近子体积偏移的增量DVC方法，该方法将参考子体积自动转换到最近的整像素位置，避免了亚像素插值中涉及的冗余计算和系统误差，解决了全场内部大变形测量的挑战性问题。

3.2 形函数的选择

在大变形问题中，特别是复杂变形问题中，零阶和一阶形函数不足以近似表达子区内部变形，这将造成显著的系统误差。构造更为适合的形函数是减小系统误差的关键。提高形函数阶数是避免欠匹配问题最直接的想法，不同阶次形函数的对比如图4所示。二阶形函数的引入能够更有效地反映子区内部潜在的复杂变形，使非均匀和大变形的测量变得可行。Lu等[26]证明了二阶形函数具有比一阶形函数更好的精度。值得注意的是，尽管系统误差得到降低，但是随机误差变得更高，为了避免较大的随机误差，一般建议使用较大的子区尺寸。二阶形函数的另一个问题是不可逆，这导致了无法直接通过普遍认为最有效平衡计算效率和测量精度的反向组合高斯牛顿法（IC–GN）进行求解。一些方法通过改进二阶形函数使可逆性得到满足，使得二阶形函数获得更广泛的应用。如：Gao等[27]将传统的二阶形函数展开，得到形函数的新分量，通过改进获得一个可逆的二阶形函数，在大变形测量时具有稳定的精度。Bai等[28]通过引入位移函数及其共轭函数，在可逆线性变换中构造了一个新的互补矩阵，从而满足IC–GN算法对二阶形函数可逆的要求，来应对图像之间的非均匀大变形；并将其与传统的二阶形函数和Gao等提出的二阶形函数进行了比较。如图5所示，发现不同二阶形函数的平均误差随着子区大小的增加而减小，当子区大小足够大时，Bai等[28]所提出的二阶形函数表现出更稳定的匹配精度，并且建议在实际应用中选择43～61像素的子区大小。一些研究侧重于自适应方法[29]，允许根据不同的变形程度选择合适的形函数，同时避免可能出现的欠匹配与过匹配风险。

图4 形函数对比

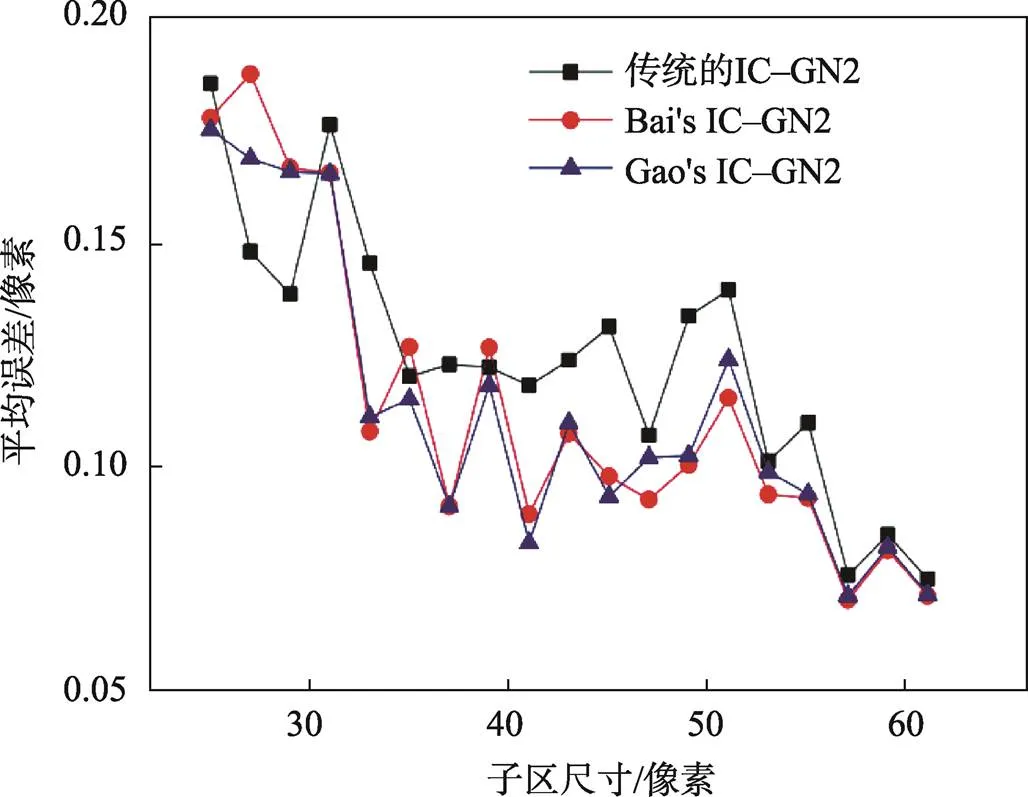
图5 3种二阶形函数的平均误差比较[28]

特殊形函数在特殊场景中具备优势，如裂纹尖端、断裂界面等。当试样发生断裂时，材料尖端裂纹的变形也相当于大变形的问题，裂纹尖端位移函数的准确表征，对裂纹尖端变形场的计算是极其重要的。江守燕等[30]基于三角变换的方法，将裂尖改进单元的4项改进函数缩减为2项，保留裂纹尖端场的应力奇异性和裂纹上、下表面的位移不连续性。Hattori等[31]对各向异性材料的裂纹尖端的扩展有限元方法进行了研究，提出了简洁而紧凑形式的富集裂尖函数。

3.3 初值估计方法

增量相关策略的累积误差主要依赖于参考图像的更新次数，提高DIC方法的变形测量能力是减小更新次数最直接的方法。由于变形程度增大导致的退相关效应，整像素搜索很难为每个计算点寻找到合适的初值。探索更可靠的初值估计方法是解决这一问题的关键。种子点位移传递策略在大变形测量中应用广泛，其基本原理如图6所示，该方法通过选取特征明显、变形较小处的计算点为种子点，以避免可能出现的退相关效应，种子点处的整像素搜索更为容易。潘兵等[32]基于位移连续性假设，通过手动指定感兴趣点周围3个或者更多的种子点，并在变形后图像中选择其对应点，将种子点的计算结果逐步传递给下一点作为初值估计，在大变形测量中十分有效。然而，遗憾的是，测量误差以相同路径传递，会造成全场变形的测量误差较大。为了克服这一缺陷，Pan等[33]又采用了可靠性引导的种子点传递策略，由于将计算队列中相关性最好的计算点作为相邻点的初值估计，确保了计算路径始终沿着最可靠的方向，极大地抑制了误差的传播。种子点的选择在该方法中至关重要，一些方法致力于种子点的自适应选择。值得一提的是，Jiang等[34]提出了路径无关的初值估计方法，通过频域中的搜索方法，极大地提高了初值估计的效率，同时避免了位移传递方法对路径的依赖性。尽管该方法适用于小变形测量，但已有一些改进用于扩大测量范围，在大变形测量中可能具备潜力。

图6 种子点传递策略初值估计和可靠性引导的原理[33]

特征检测算法具有灵活、灵敏、计算和预测能力强等优点，在大变形测量问题中具有广泛的应用前景。通过特征检测算法和DIC方法的结合为大变形测量问题提供了鲁棒性更强的初值估计方法，其基本原理如图7a所示。Zhou等[35]和Wang等[36]引入SIFT算法对特征点进行提取，在参考图像和变形图像中匹配检测到的特征点，随后采用随机抽样一致算法（Random Sample Consensus, RANSAC）剔除错误匹配，完成种子点的变形估计。然而SIFT算法的特征提取和匹配非常耗时，限制了SIFT辅助DIC的应用。一些方法通过应用并行算法加速SIFT来辅助DIC，取得了较好的效果。Yang等[37]提出一种基于SIFT算法辅助的路径无关的DIC方法，并通过引入图形处理单元GPU或多核CPU的并行计算来加速，提高了计算效率。另外一些方法使用更为高效的特征提取算法作为改进，如：Zou等[38]提出了应用SURF算法结合可靠性引导位移跟踪策略应对较大变形的测量；李慧等[39]提出首先对匹配图像进行网格划分，利用ORB算法[40]提取特征点，然后应用双边特征匹配来剔除错误匹配，最后独立估计每个感兴趣点的变形参数，为亚像素迭代提供初值估计；Zhang等[41]将ORB算法与特征引导的高斯混合模型点集匹配算法（FG–GMM）相结合，提出了一种基于特征的初始猜测（FB–IG）方案，应用RKHS函数在参考图像的特征点上对全局连续变形场进行内插，用期望和最大化算法求解优化问题后，同时确定正确的特征对和不均匀的变形场，该算法应用于大变形或旋转的情况下具有鲁棒性；谭芳喜等[42]利用AKAZE特征提取算法结合Daisy特征描述符，实现更加密集的特征提取，提高DIC技术定位的准确性，而且计算效率更高；Li等[43]结合DASIY特征描述符和PatchMatch搜索方法也提高了基于特征提取算法的DIC技术对大变形测量的效率。同样为了解决特征提取算法耗时的问题，Wang等[44]在初值估计处理方面提出利用小波金字塔的多分辨率分析方法，如图7b所示，多分辨率小波金字塔在低分辨率层将原始图像缩小为小图像，在低分辨率层计算2幅图像之间的相关系数，大大减少了传统逐像素匹配算法的计算量。

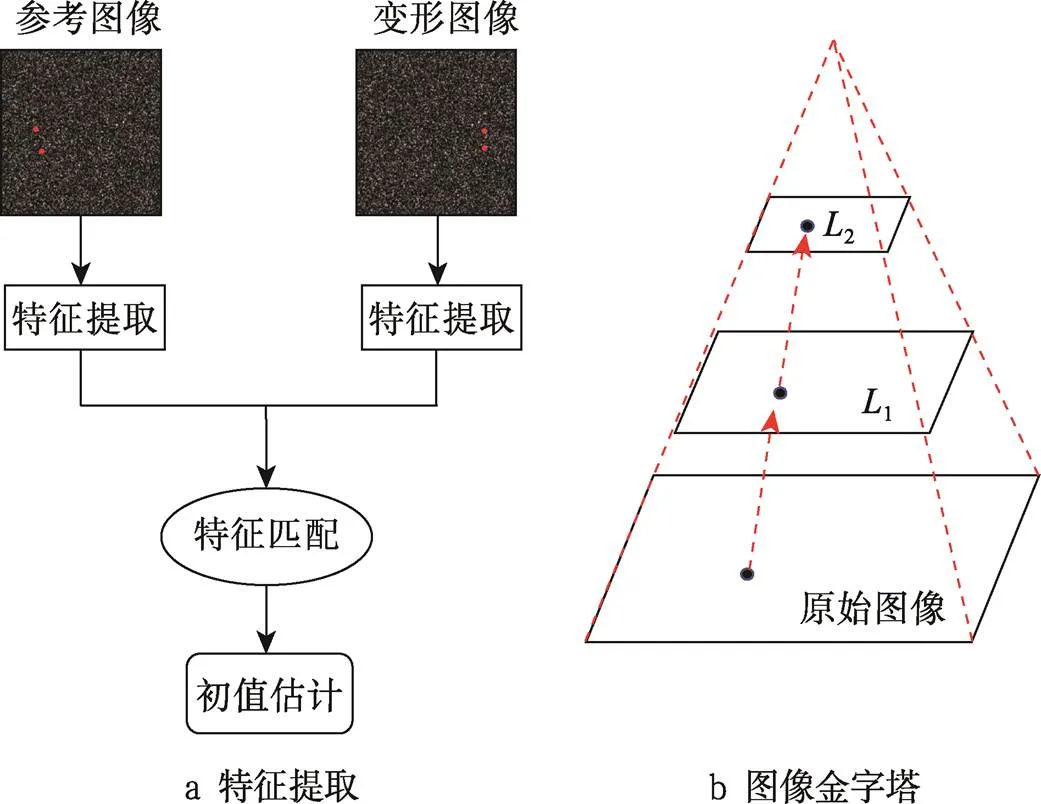
图7 特征提取和图像金字塔的原理图

DIC技术对试件大旋转测量，存在着与大变形测量相同的问题。为了解决这一难题，Zhang等[21]提出采用环形模板匹配图像来初值估计，如图8所示，提出的环形模板具有旋转不变性和平移不变性。传统的DIC计算缺少与旋转有关的参数，为了满足DIC技术对大旋转测量的要求，Zhong等[45]将笛卡尔坐标系下的旋转测量转换为极坐标下的平移测量，该方法中，参考子区和变形子区的形状都被定义为一个圆，然后这些子区被用极坐标来描述。将种子点或搜索点的梯度方向定义为极坐标中新的0°方向，采用了高效的IC–GN算法获取亚像素精度。迭代初值通过考虑种子点和搜索点的梯度方向之间的误差来获得关于旋转的参数，对于大旋转的测量，迭代的初值更准确，迭代收敛更快。

3.4 预变形辅助策略

种子点初值估计、位移传递策略和高阶形函数是大变形DIC方法普遍采用的策略，然而，尽管高阶形函数可以用于描述复杂的变形，但由于涉及的变量增多，其计算成本也将迅速增加。同时由于过匹配现象的存在，导致形函数阶数的增加并不一定能够增加测量精度。这意味着，即使有足够良好的初值估计，简单地增加形函数阶数也不足以解决大变形问题。基于此，Ye等[46]通过在散斑图像边缘设置人工标记点，基于拟共形映射计算了稳健的大变形初值，并通过将初值估计引入ZNSSD相关函数中，得到了大变形适用的DIC方法。随后，叶敬晨[47]扩展了这一想法，开发出预变形辅助策略。如图9所示，该方法将形分解为预变形和后变形两部分，初值估计用于给出预变形，该预变形能够描述试样变形中潜在的非线性部分，从而使后变形能够在DIC框架中得到更可靠地测量。预变形策略在使用低阶形函数的同时，保留了描述子区变形中潜在非线性的能力，在大变形测量中具备潜力。

图8 环形模板示意图

图9 预变形分解示意图[47]

3.5 基于深度学习的DIC方法

深度学习是一种用于复杂任务数据驱动的模型，是处理图像相关问题的重要工具。深度学习应用于DIC方法中，不需要特定的相关准则，也不需要进行数值迭代计算，大大提高了DIC相关计算的效率。Yang等[48]利用2个卷积神经网络，即位移神经网络（DisplacementNet）和应变神经网络（StrainNet）一起工作，对位移和应变进行端到端的预测，如图10所示；位移神经网络预测位移场并自适应地更新感兴趣区域以跟踪大变形，而应变神经网络直接从图像输入中预测应变场，不依赖于位移预测，显著提高了应变预测精度。Wu等[49]为了将应变分布映射到发生的相应裂缝上，将DIC应变分布数据应用到深度残余网络（ResNet），以训练一个回归模型，实现实时检测裂缝的发生情况并估计裂缝长度。深度学习可以解决DIC计算过程中的非线性优化问题，为DIC迭代问题提供了新的解决思路，Duan等[50]采用二阶形函数创建训练数据集，开发了一种新的基于卷积神经网络的DIC分析理论框架（DIC–net）。训练成功后的DIC–net更适合求解局部非线性变形场，实现高效的图像匹配和位移场重构，为实时处理复杂大变形提供了指导意义。深度学习应用在DIC中，提高了计算效率，但是由于训练数据集的限制，在实际过程中计算的精度可能并未得到实质性的改变。随着继续对深度学习方法在DIC领域的深入研究，深度学习强大的计算和预测能力，会在DIC领域大有可为。

图10 位移/应变卷积神经网络原理

4 大变形DIC的应用举例

4.1 在包装领域中的应用

在包装工程领域，一些包装材料质轻而柔软，在外载荷作用下通常应变量很大并且为非线性的，很难测试其力学性能，同时应变片法测量会使胶水中的水分子渗入到纸板中影响结果的准确性，引伸计的夹具也会对测量产生影响；为了克服这些困难，可以通过非接触的DIC技术测量包装材料的力学性能。Kueh等[51]使用DIC技术，对瓦楞纸箱纵向压缩过程中面板位移和变形情况进行测试，得到箱体应变分布情况。Fadiji等[52]利用DIC技术测量通风包装箱在机械载荷作用下的位移场，考虑了不同几何构型气孔的影响，加深对瓦楞纸板包装在压缩载荷作用下的位移场和应变场的认识，证明DIC在压缩载荷下研究通风包装箱的失效机制方面存在潜在价值，为新鲜农产品包装箱的机械设计提供了指导。Zhou等[53]综合测量了聚丙烯包装材料的应力–应变关系、泊松比、线膨胀性、蠕变特性、全场变形、低频振动，证明了DIC方法在包装材料上具有测量范围广、精度高、稳定性好等优点。赵钊等[54]利用DIC方法对高速相机采集的纸浆模塑托盘在不同高度跌落图像进行定量分析，发现纸浆模塑托盘在跌落缓冲过程中主要发生塑性变形，不同的跌落高度对弹性变形影响不大，这为纸浆模塑托盘的设计提供了重要指导。储信庆等[55]将DIC方法与单项拉伸实验相结合，对白板纸和白卡纸拉伸前后的图像进行分析，测量其泊松比；通过力–位移曲线得到其弹性模量，分析得到同种纸张中，定量越高，其弹性模量越大，而泊松比越小。

4.2 在结构工程领域中的应用

桥梁挠度直接反映了桥梁结构的整体垂直刚度，与承载能力和承受外部破坏荷载的能力密切相关，在桥梁的日常安全评估中，桥梁的静态和动态挠度是其测量的基本参数。针对土木工程结构大变形非接触测量的需要，Pan等[56]基于IC–GN算法结合激光测距仪设计了一种视频挠度计，通过对桥梁的变形测量，证明了该视频挠度计可以测量存在多个垂直偏转点测试对象的变形场，同时验证了该视频挠度计在实际、远距离、非接触实验中的实用性和有效性。Mohammed等[57]通过搭建适用于工程实际测量的自标定图像相关系统，基于DIC技术对榫卯构件进行了大面积的全场变形测量，获得了构件的变形分布以及构件在破坏过程中的变形情况。针对桥梁挠度的长期监测需要，Zhang等[58]通过DIC技术并结合声发射技术，了解桥梁之间板梁的开裂和抗剪承载性能，通过DIC技术揭示了桥梁在剪切破坏时的结构变化。Howlader等[59]应用DIC方法对含开口的无筋砌筑墙体的变形进行了测量并且捕获砖石的全场裂缝。Nouri等[60]使用DIC技术对无箍筋钢筋混凝土梁的抗剪强度各分量进行了测量研究，并且就计算模型对不同梁的计算情况进行了评价。Zhang等[61]利用DIC技术对钢筋混凝土结构角部开裂的机理和过程进行了实验研究，记录了拐角开裂的整个过程和拐角开裂的旋转现象，研究结果有助于理解腐蚀引起拐角开裂的机理和过程，开发精确的模型来评估钢筋混凝土结构的使用寿命。

4.3 在软材料领域中的应用

在软材料上，考虑到油漆涂层，会增加局部刚度，减小表面变形的影响，Casavola等[62]利用材料自身存在的膨胀石墨作为自然随机散斑，对3种密度不同的软开孔聚氨酯泡沫塑料通过增量相关策略完成大变形的测量，并对其力学性能进行分析与评价。正确估计大变形下非线性材料的断裂参数是断裂力学的主要难题之一，裂纹尖端检测受裂纹尖端纤维的影响显著，导致测量不准确；为了克服这一限制，Filho等[63]提出基于DIC方法的纤维软复合材料裂纹尖端检测的新方法，并与视觉检测方法进行了比较，表明所提出的方法可扩展到其他生物纤维软材料的可行性。开孔聚氨酯泡沫的力学性能受微观结构的影响很大，Belda等[64]为了探究开孔聚氨酯泡沫在微观尺度上的破坏机制和变形模式表征，利用DIC技术测量了3种不同密度的开孔聚氨酯泡沫塑料在压缩试验中的应变场，得到DIC参数对失效模型和表观极限点的影响，为破坏机制的确定和微观尺度上变形模型的表征提供指导作用。水凝胶等弹性体在外力作用下通常表现较大的变形，常规的方法很难对其进行机械表征，而DIC技术却表现出很强的适用性，Millar等[65]利用DIC技术测试了4种不同浓度的琼脂糖水凝胶的机械剪切性能，发现随着凝胶浓度的增加，剪切模量和最大剪切应变增加，证明了DIC技术在凝胶软材料方面的适用性。

4.4 在高温测量领域中的应用

试样在高温下会发生大的塑性变形，常用的人造散斑图案可能会在颈缩后脱落，此外，涂料的厚度可能导致对试样的真实应变测量不准确，因此，Zheng等[66]利用激光散斑技术，采用RG–DIC方法对金属在高温下的局部大塑性变形进行了定性和定量评价。飞机在大气层中飞行时，由于剧烈的气动摩擦，其外表面会处于恶劣的高温环境中，在高温环境下测量飞机部件受热表面的变形是重要的问题；基于这一难题，Wu等[67]利用DIC方法测量了飞机外表面在1 200 ℃的高温环境下的应变分布，为飞机部件的热强度分析以及安全可靠设计提供了重要依据。Rooyen等[68]利用DIC技术测量了在温度高达900 ℃下铬钢的变形，在480～600 ℃内获得试件的弹性模量和泊松比。Le等[69]通过DIC技术测定了混凝土结构在高温下的变形，为混凝土结构改进防火性能提供指导。Kaczmarek等[70]利用DIC技术分别检测耐火陶瓷在20～1 200 ℃的断裂行为，结果表明，材料在1 200 ℃时比在室温下表现出更多的裂纹分枝。Xie等[71]结合DIC技术和扫描电子显微镜，对750 ℃下镍基单晶高温合金的变形进行裂纹的扩展过程捕捉，通过显微观察和DIC测量，有助于进一步了解材料的失效机制。

5 结语

DIC技术作为重要的非接触全场变形测量手段，在许多领域中广泛采用，但在大变形测量方面所面临的挑战限制了DIC方法的进一步发展。通过对增量相关、初值估计、形函数、预变形以及深度学习方面等一系列改进措施的研究，面向大变形测量的DIC方法取得了较大的进步。当前，大变形DIC方法的发展仍然受到退相关效应和欠匹配问题的严重影响，面临着诸多挑战。为了进一步提高大变形DIC方法的测量精度，还需要在以下方面做进一步的研究：进一步引入其他测量技术来辅助实现大变形测量；在形函数的处理上，大部分只是对二阶形函数进行改进，对更高阶形函数的研究仍不够深入；预变形是一种对处理大变形问题新颖的想法，对预变形优化处理方法有待继续挖掘，将预变形与增量相关方法结合起来共同处理更新后参考图像的方法，也将进一步提高DIC计算的精度。可以预测，DIC方法将在大变形测量中发挥更重要的作用。

[1] CHENG Hao, XU Hao, JULIAN MCCLEMENTS D, et al. Recent Advances in Intelligent Food Packaging Materials: Principles, Preparation and Applications[J]. Food Chemistry, 2022, 375: 131738.

[2] WEITZ D A. Soft Materials Evolution and Revolution[J]. Nature Materials, 2022, 21(9): 986-988.

[3] WEYMANN A, FOROUGHI J, VARDANYAN R, et al. Artificial Muscles and Soft Robotic Devices for Treatment of End-Stage Heart Failure[J]. Advanced Materials (Deerfield Beach, Fla), 2022: 2207390.

[4] LI Yi-ding, YAN Shi-bo, YAN Ying, et al. Modelling of the Compressive Behavior of 3D Braided Tubular Composites by a Novel Unit Cell[J]. Composite Structures, 2022, 287: 115303.

[5] ZHANG Bo-yi, WANG Li, ZHANG Jian, et al. Deformation and Energy Absorption Properties of Cenosphere/Aluminum Syntactic Foam-Filled Circular Tubes under Lateral Quasi-Static Compression[J]. International Journal of Mechanical Sciences, 2021, 192: 106126.

[6] WICKRAMASINGHE K C, SASAHARA H, RAHIM E A, et al. Recent Advances on High Performance Machining of Aerospace Materials and Composites Using Vegetable Oil-Based Metal Working Fluids[J]. Journal of Cleaner Production, 2021, 310: 127459.

[7] KOOHBOR B, MONTGOMERY C B, SOTTOS N R. Identification of RVE Length Scale in Fiber Composites via Combined Optical and SEM Digital Image Correlation[J]. Composites Science and Technology, 2022, 227: 109613.

[8] SPENCER R, ALWEKAR S, JO E, et al. Fiber Orientation Evaluation in Reinforced Composites Using Digital Image Correlation and Thermal Excitation[J]. Composites Part B: Engineering, 2022, 234: 109713.

[9] MALLETT K F, ARRUDA E M. Digital Image Correlation-Aided Mechanical Characterization of the Anteromedial and Posterolateral Bundles of the Anterior Cruciate Ligament[J]. Acta Biomaterialia, 2017, 56: 44-57.

[10] KELLY B P, SILVA C R, LEHRMAN J N, et al. Use of Digital Imaging Correlation Techniques for Full-Field Strain Distribution Analysis of Implantable Devices and Tissue in Spinal Biomechanics Research[J]. Journal of Biomechanics, 2022, 135: 111025.

[11] JIN Zu-quan, LI Shi-cai, SONG Hua-miao, et al. Experimental and Simulative Study of Bonding Properties on Fiber/Epoxy Interfaces by Digital Image Correlation (DIC) Technique and Molecular Dynamics[J]. Cement and Concrete Composites, 2022, 131: 104569.

[12] ZHAO Yin-ming, TAN Si-yang, ZHANG Chao-fan, et al. Dependence of Creep Strain and Fatigue Behavior on Surface Characteristics of Resistive Strain Gauges[J]. Micromachines, 2022, 13(3): 379.

[13] CHEN Chang-fu, MAO Feng-shan, YU Jia-yong. A Digital Image Correlation-Aided Sampling Moiré Method for High-Accurate In-Plane Displacement Measurements[J]. Measurement, 2021, 182: 109699.

[14] LI Zhi-song, ZHONG Ping, CHEN Yu, et al. Simultaneous Measurement of Three-Dimensional Deformation Based on Digital Speckle Pattern Interferometry Technology[J]. Optics Communications, 2021, 480: 126423.

[15] PETERS W H, RANSON W F. Digital Imaging Techniques in Experimental Stress Analysis[J]. Optical Engineering, 1982, 21(3): 427-431.

[16] YAMAGUCHI I. A Laser-Speckle Strain Gauge[J]. Journal of Physics E: Scientific Instruments, 1981, 14(11): 1270-1273.

[17] WANG Qi-yu, CHEN Sheng-hu, LV Xin-liang, et al. Role of Δ-Ferrite in Fatigue Crack Growth of AISI 316 Austenitic Stainless Steel[J]. Journal of Materials Science & Technology, 2022, 114: 7-15.

[18] GAO Jin-ling, KIRK C D, KEDIR N, et al. A Method for Characterization of Multiple Dynamic Constitutive Parameters of FRCS[J]. Composites Science and Technology, 2021, 203: 108607.

[19] MA Chun-yang, DU Tian-ming, NIU Xu-feng, et al. Biomechanics and Mechanobiology of the Bone Matrix[J]. Bone Research, 2022, 10(1): 59.

[20] HUANG Yang, JI Jing-jing, LEE K M. Model-Based Digital Image Correlation for Noncontact Deformation Measurement of Strain Field and Mechanical Property[J]. IEEE Transactions on Industrial Informatics, 2019, 15(9): 5109-5118.

[21] ZHANG Xiao-chuan, CHEN Jin-long, WANG Zong-tao, et al. Digital Image Correlation Using Ring Template and Quadrilateral Element for Large Rotation Measurement[J]. Optics and Lasers in Engineering, 2012, 50(7): 922-928.

[22] PAN Bing, WU Da-fang, XIA Yong. Incremental Calculation for Large Deformation Measurement Using Reliability-Guided Digital Image Correlation[J]. Optics and Lasers in Engineering, 2012, 50(4): 586-592.

[23] TANG Zheng-zong, LIANG Jin, XIAO Zhen-zhong, et al. Large Deformation Measurement Scheme for 3D Digital Image Correlation Method[J]. Optics and Lasers in Engineering, 2012, 50(2): 122-130.

[24] ZHOU Yi-hao, SUN Chen, CHEN Ju-bing. Adaptive Subset Offset for Systematic Error Reduction in Incremental Digital Image Correlation[J]. Optics and Lasers in Engineering, 2014, 55: 5-11.

[25] WANG Bo, PAN Bing. Incremental Digital Volume Correlation Method with Nearest Subvolume Offset: An Accurate and Simple Approach for Large Deformation Measurement[J]. Advances in Engineering Software, 2018, 116: 80-88.

[26] LU H, CARY P D. Deformation Measurements by Digital Image Correlation: Implementation of a Second-Order Displacement Gradient[J]. Experimental Mechanics, 2000, 40(4): 393-400.

[27] GAO Yue, CHENG Teng, SU Yong, et al. High-Efficiency and High-Accuracy Digital Image Correlation for Three- Dimensional Measurement[J]. Optics and Lasers in Engineering, 2015, 65: 73-80.

[28] BAI Rui-xiang, JIANG Hao, LEI Zhen-kun, et al. A Novel 2nd-Order Shape Function Based Digital Image Correlation Method for Large Deformation Measurements[J]. Optics and Lasers in Engineering, 2017, 90: 48-58.

[29] ZHAO Jian. Deformation Measurement Using Digital Image Correlation by Adaptively Adjusting the Parameters[J]. Optical Engineering, 2016, 55(12): 124104.

[30] 江守燕, 杜成斌. 一种XFEM断裂分析的裂尖单元新型改进函数[J]. 力学学报, 2013, 45(1): 134-138.

JIANG Shou-yan, DU Cheng-bin. A Novel Enriched Function of Elements Containing Crack Tip for Fracture Analysis in Xfem[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(1): 134-138.

[31] HATTORI G, ROJAS-DÍAZ R, SÁEZ A, et al. New Anisotropic Crack-Tip Enrichment Functions for the Extended Finite Element Method[J]. Computational Mechanics, 2012, 50(5): 591-601.

[32] 潘兵, 谢惠民, 夏勇, 等. 数字图像相关中基于可靠变形初值估计的大变形测量[J]. 光学学报, 2009, 29(2): 400-406.

PAN Bing, XIE Hui-min, XIA Yong, et al. Large-Deformation Measurement Based on Reliable Initial Guess in Digital Image Correlation Method[J]. Acta Optica Sinica, 2009, 29(2): 400-406.

[33] PAN Bing. Reliability-Guided Digital Image Correlation for Image Deformation Measurement[J]. Applied Optics, 2009, 48(8): 1535-1542.

[34] JIANG Zhen-yu, QIAN Ke-mao, MIAO Hong, et al. Path-Independent Digital Image Correlation with High Accuracy, Speed and Robustness[J]. Optics and Lasers in Engineering, 2015, 65: 93-102.

[35] ZHOU Yi-hao, PAN Bing, CHEN Yan qiu. Large Deformation Measurement Using Digital Image Correlation: A Fully Automated Approach[J]. Applied Optics, 2012, 51(31): 7674-7683.

[36] WANG Z, VO M, KIEU H, et al. Automated Fast Initial Guess in Digital Image Correlation[J]. Strain, 2014, 50(1): 28-36.

[37] YANG Jun-rong, HUANG Jian-wen, JIANG Zhen-yu, et al. SIFT-Aided Path-Independent Digital Image Correlation Accelerated by Parallel Computing[J]. Optics and Lasers in Engineering, 2020, 127: 105964.

[38] ZOU Xiang, PAN Bing. Full-Automatic Seed Point Selection and Initialization for Digital Image Correlation Robust to Large Rotation and Deformation[J]. Optics and Lasers in Engineering, 2021, 138: 106432.

[39] 李慧, 顾永刚, 翟超. 一种基于DIC测量帧间大压缩变形的方法[J]. 工业控制计算机, 2021, 34(8): 90-92.

LI Hui, GU Yong-gang, ZHAI Chao. A Method for Measuring Large Inter-Frame Compression Deformation Based on DIC[J]. Industrial Control Computer, 2021, 34(8): 90-92.

[40] LIU Kai, XU Zheng, HOU Zhao-hui, et al. Further Non-Local and Channel Attention Networks for Vehicle re-Identification[C]// 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW) Seattle, WA, USA, IEEE, 2020: 2494-2500.

[41] ZHANG Yun-lu, YAN Lei, LIOU F. Improved Initial Guess with Semi-Subpixel Level Accuracy in Digital Image Correlation by Feature-Based Method[J]. Optics and Lasers in Engineering, 2018, 104: 149-158.

[42] 谭芳喜, 肖世德, 李晟尧, 等. 基于密集特征匹配的数字图像相关法[J]. 激光与光电子学进展, 2021, 58(16): 390-398.

TAN Fang-xi, XIAO Shi-de, LI Sheng-yao, et al. Digital Image Correlation Method Based on Dense Feature Matching[J]. Laser & Optoelectronics Progress, 2021, 58(16): 390-398.

[43] LI Wen-pan, LI You-fu, LIANG Jin. Enhanced Feature-Based Path-Independent Initial Value Estimation for Robust Point-Wise Digital Image Correlation[J]. Optics and Lasers in Engineering, 2019, 121: 189-202.

[44] WANG Lian-po, BI Song-lin, LI Hui, et al. Fast Initial Value Estimation in Digital Image Correlation for Large Rotation Measurement[J]. Optics and Lasers in Engineering, 2020, 127: 105838.

[45] ZHONG F, QUAN C. Digital Image Correlation in Polar Coordinate Robust to a Large Rotation[J]. Optics and Lasers in Engineering, 2017, 98: 153-158.

[46] YE Jing-chen, JI Hong-wei, ZHANG Xiao-chuan. Digital Image Correlation Method Based on Quasi-Conformal Mapping for Large Deformation Measurement[J]. Optics and Lasers in Engineering, 2022, 153: 106985.

[47] 叶敬晨. 面向大变形测量的数字图像相关方法研究[D]. 天津: 天津商业大学, 2022: 14-15.

YE Jing-chen. Research on Digital Image Correlation Method for Large Deformation Measurement[D]. Tianjin: Tianjin University of Commerce, 2022: 14-15.

[48] YANG Ru, LI Yang, ZENG D, et al. Deep DIC: Deep Learning-Based Digital Image Correlation for End-to-End Displacement and Strain Measurement[J]. Journal of Materials Processing Technology, 2022, 302: 117474.

[49] WU Zi-ran, HAN Yan, LIANG Bu-meng, et al. A Metallic Fracture Estimation Method Using Digital Image Correlation[J]. Processes, 2022, 10(8): 1599.

[50] DUAN Xiao-cen, XU Hong-wei, DONG Run-feng, et al. Digital Image Correlation Based on Convolutional Neural Networks[J]. Optics and Lasers in Engineering, 2023, 160: 107234.

[51] KUEH C S L, DAHM K, EMMS G, et al. Digital Image Correlation Analysis of Vertical Strain for Corrugated Fiberboard Box Panel in Compression[J]. Packaging Technology and Science, 2019, 32(3): 133-141.

[52] FADIJI T, COETZEE C J, OPARA U L. Evaluating the Displacement Field of Paperboard Packages Subjected to Compression Loading Using Digital Image Correlation (DIC)[J]. Food and Bioproducts Processing, 2020, 123: 60-71.

[53] ZHOU Jian-wei, LIU Dong-hong, SHAO Lan-yuan, et al. Application of Digital Image Correlation to Measurement of Packaging Material Mechanical Properties[J]. Mathematical Problems in Engineering, 2013, 2013: 1-8.

[54] 赵钊, 张晓川, 王佼, 等. 纸浆模塑托盘对角刚度的跌落试验测试[J]. 包装工程, 2012, 33(11): 1-4.

ZHAO Zhao, ZHANG Xiao-chuan, WANG Jiao, et al. Drop Test of Molded Pulp Pallet and Diagonal Stiffness Analysis[J]. Packaging Engineering, 2012, 33(11): 1-4.

[55] 储信庆, 计宏伟. 灰底白板纸与白卡纸的弹性常数对比[J]. 包装工程, 2015, 36(23): 48-52.

CHU Xin-qing, JI Hong-wei. Comparison of the Elastic Constants between the Gray Manila Board and Ivory Board[J]. Packaging Engineering, 2015, 36(23): 48-52.

[56] PAN Bing, TIAN Long, SONG Xiao-lin. Real-Time, Non-Contact and Targetless Measurement of Vertical Deflection of Bridges Using Off-Axis Digital Image Correlation[J]. NDT & E International, 2016, 79: 73-80.

[57] MOHAMMED M E, 邵新星, 钱帅宇, 等. 基于自标定数字图像相关技术的榫卯构件大面积全场变形测量[J]. 东南大学学报(自然科学版), 2018, 48(2): 337-341.

MOHAMMED M E, SHAO Xin-xing, QIAN Shuai-yu, et al. Large-Area Full-Field Deformation Measurement of Mortise-Tenon Structures Based on Self-Calibration Digital Image Correlation Technology[J]. Journal of Southeast University (Natural Science Edition), 2018, 48(2): 337-341.

[58] ZHANG Feng-qiao, ZARATE GARNICA G I, YANG Yu-guang, et al. Monitoring Shear Behavior of Prestressed Concrete Bridge Girders Using Acoustic Emission and Digital Image Correlation[J]. Sensors (Basel, Switzerland), 2020, 20(19): 5622.

[59] HOWLADER M K, MASIA M J, GRIFFITH M C. Digital Image Correlation for the Analysis of In-Plane Tested Unreinforced Masonry Walls[J]. Structures, 2021, 29: 427-445.

[60] NOURI A, HAMRAT M, BOULEKBACHE B, et al. Quantification of Shear Strength in Reinforced Concrete Beams Using Digital Image Correlation: Experimental and Analytical Study[J]. Advances in Structural Engineering, 2021, 24(1): 147-164.

[61] ZHANG Yan-long, SU R K L. Experimental Study of Corrosion-Caused Corner Cracking Using Digital Image Correlation[J]. Materials and Structures, 2022, 55(4): 121.

[62] CASAVOLA C, CORE L, MORAMARCO V, et al. Full-Field Mechanical Characterization of Polyurethane Foams under Large Deformations by Digital Image Correlation[J]. Mechanics of Advanced Materials and Structures, 2022, 29(24): 3540-3555.

[63] FILHO J, XAVIER J, NUNES L. An Alternative Digital Image Correlation-Based Experimental Approach to Estimate Fracture Parameters in Fibrous Soft Materials[J]. Materials (Basel, Switzerland), 2022, 15(7): 2413.

[64] BELDA R, MEGÍAS R, FEITO N, et al. Some Practical Considerations for Compression Failure Characterization of Open-Cell Polyurethane Foams Using Digital Image Correlation[J]. Sensors (Basel, Switzerland), 2020, 20(15): 4141.

[65] MILLAR D, MENNU M, UPADHYAY K, et al. An Improved Direct Shear Characterisation Technique for Soft Gelatinous and Elastomeric Materials[J]. Strain, 2021, 57(3): 12383.

[66] ZHENG Qiu, MASHIWA N, FURUSHIMA T. Evaluation of Large Plastic Deformation for Metals by a Non-Contacting Technique Using Digital Image Correlation with Laser Speckles[J]. Materials & Design, 2020, 191: 108626.

[67] WU Da-fang, LIN Lu-jin, REN Hao-yuan, et al. High-Temperature Deformation Measurement of the Heated Front Surface of Hypersonic Aircraft Component at 1200[J]. Optics and Lasers in Engineering, 2019, 122: 184-194.

[68] ROOYEN M V, BECKER T H. High-Temperature Tensile Property Measurements Using Digital Image Correlation over a Non-Uniform Temperature Field[J]. The Journal of Strain Analysis for Engineering Design, 2018, 53(3): 117-129.

[69] LE D B, TRAN S D, TORERO J L, et al. Application of Digital Image Correlation System for Reliable Deformation Measurement of Concrete Structures at High Temperatures[J]. Engineering Structures, 2019, 192: 181-189.

[70] KACZMAREK R, DUPRÉ J C, DOUMALIN P, et al. High-Temperature Digital Image Correlation Techniques for Full-Field Strain and Crack Length Measurement on Ceramics at 1 200 ℃: Optimization of Speckle Pattern and Uncertainty Assessment[J]. Optics and Lasers in Engineering, 2021, 146: 106716.

[71] XIE Hong-fu, WANG Jie, WANG Zhen, et al. In Situ Scanning Digital Image Correlation for high-Temperature Deformation Measurement of Nickel-Based Single Crystal Superalloy[J]. Measurement Science and Technology, 2021, 32(8): 084008.

Research Progress and Application of Digital Image Correlation for Large Deformation Measurement

LI Jia-chenga, YE Jing-chenb, JI Hong-weib

(a. College of Biotechnology and Food Science b. College of Mechanical Engineering, Tianjin University of Commerce, Tianjin 300134, China)

The work aims to study the research status of Digital Image Correlation (DIC) for large deformation measurement and provide references for in-depth research in related fields. Through improved combing of incremental correlation, initial value estimation and form function, the research progress of the DIC method in large deformation measurement was summarized. The current DIC method used for large deformation measurements greatly eliminated the de-correlation effect through the increment method and the initial value estimation method combined with feature detection. At the same time, the choice of shape functions and the combination of deep learning techniques also enhanced the applicability of the DIC method to complex deformations. Despite the many challenges in large deformation measurement, the DIC method is still one of the most promising techniques for large deformation measurement, and it will play a more vital role in large deformation measurement.

digital image correlation (DIC); large deformation measurement; shape function; initial value estimation

TB487

A

1001-3563(2023)05-0171-10

10.19554/j.cnki.1001-3563.2023.05.022

2022−10−09

国家自然科学基金（12172254）

李佳成（1997—），男，硕士生，主攻轻工装备设计理论与方法。

计宏伟（1964—），男，博士，教授，主攻运输包装及图像测量技术。

责任编辑：曾钰婵